In this article, we shall show you how to calculate variance in Excel. Variance is one of the most useful concepts in statistics. It gives the measurement of how the numbers of data are distributed about the mean/expected value. It measures the distribution by looking at all the data points. Here, we will analyze different methods and functions for calculating variance in Excel.
Introduction to Variance
Normally variance is the difference between an expected and actual result. In statistics, the variance is calculated by dividing the square of the deviation about the mean by the number of the population. To calculate the deviation from the mean the difference of each individual value with the arithmetic mean is taken and then all the differences are summed up.
Classification of Variance
Variance can be classified into 3 categories. They are:
- Percentage Variance
- Population Variance
- Sample Variance
In this tutorial, we will learn to calculate all of them by different methods.
How to Calculate Variance in Excel: 3 Handy Approaches
This article will guide you to calculate variance in Excel with 3 handy approaches. To demonstrate the approaches we will use some Excellent examples with explanations. Here, we will use both the manual process and the built-in Excel functions to calculate the variance. So, without further delay, let’s get started.
1. Use Excel ABS Function to Calculate Percentage Variance
In the first approach, we will calculate the percentage variance between two numbers in Excel using the ABS function. The main formula for determining percentage variance is,
Variance = (New value-Original value)/Original value
If the original value is greater than the new value, you will get a negative result. To avoid the negative result, we will use the function ABS in the formula. It makes the negative number positive. So the formula will become,
Variance = ABS(New value-Original value)/Original value
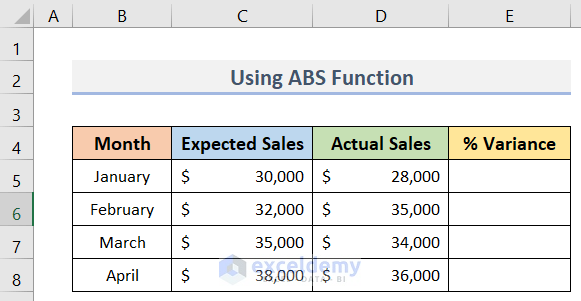
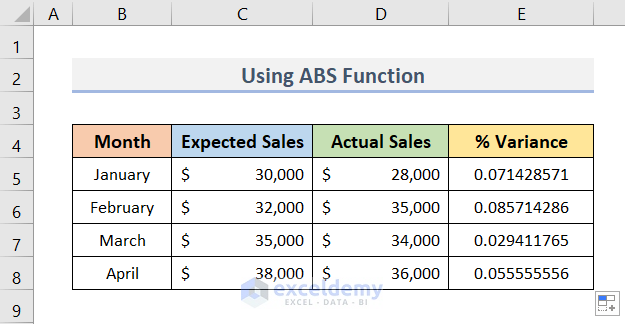
Suppose, we have a dataset (B4:E8) in Excel that contains the Expected & Actual Sales of some months. Now, we need to calculate the % Variance of those Expected & Actual Sales. See the steps below to do so.
Steps:
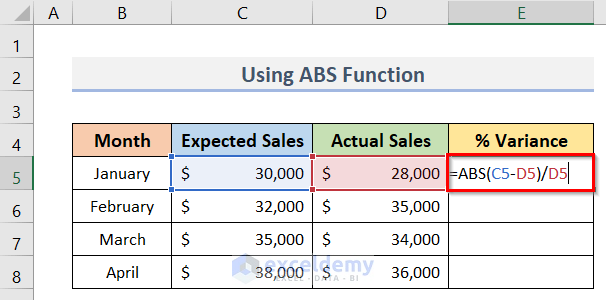
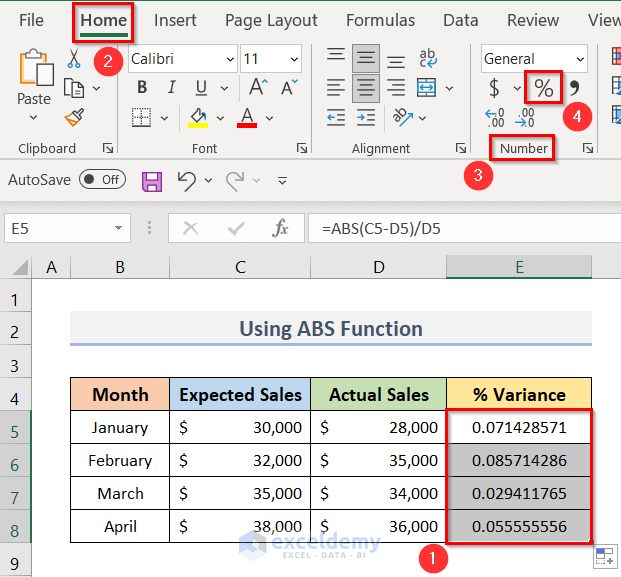
- Firstly, select cell E5.
- Next, to calculate the variance, type the following formula in cell E5:
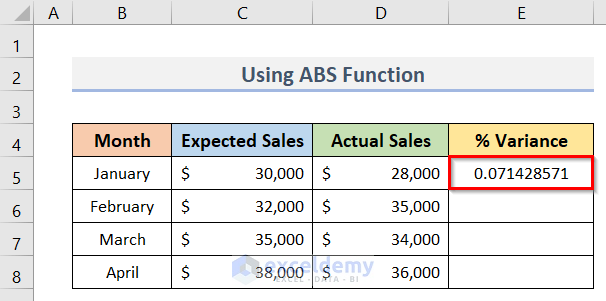
=ABS(C5-D5)/D5- After that, press the Enter key.
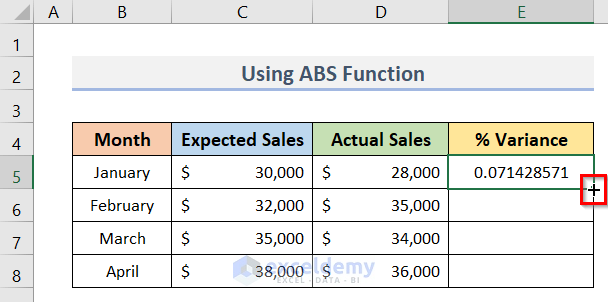
- Then, double-click on the plus (+) sign located at the bottom right corner of cell E5 to AutoFill the rest of the cells (see screenshot).
- Hence, we will get all the variances (E5:E8).
- In the following picture, we can see that the variances are decimal numbers.
- But, we need a percentage variance.
- To get the variances in percentage format, select range E5:E8 > go to the Home tab > Number group > click on the ‘%’ symbol.
- See the screenshot below for a better understanding.
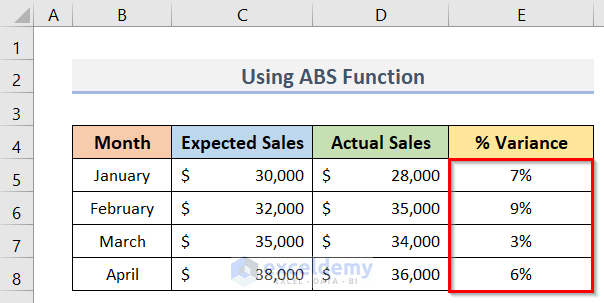
- Finally, we can see the percentage variances (E5:E8) in the screenshot below.
Read How to Calculate Mean Variance and Standard Deviation in ExcelMore: How to Do Variance Analysis in Excel
2. Calculate Population Variance in Excel
Here, we will calculate population variance in Excel. To do so, we will first apply manual calculation and then use the built-in Excel functions. The two ways are explained below.
2.1 Manual Calculation
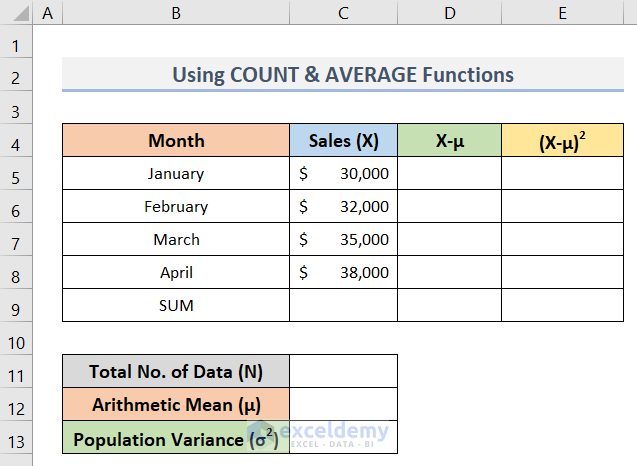
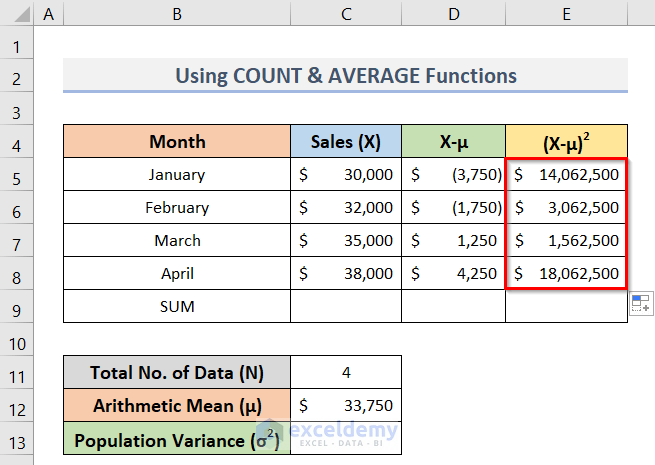
Let’s say, we have a dataset in Excel containing the Sales values of some months (see screenshot). Now, we need to calculate the population variance of the Sales (C5:C8) in cell C13. Here, we will use the COUNT, AVERAGE & SUM functions in Excel to do so.
The main formula for calculating population variance is:
Here,
- μ is the arithmetic mean.
- X is the individual value.
- N is the size of the population.
- σ2 is the population variance.
See the steps below to calculate the population variance manually.
Steps:
- For easier calculation, first, make two columns which are for (X-μ) and (X-μ)2.
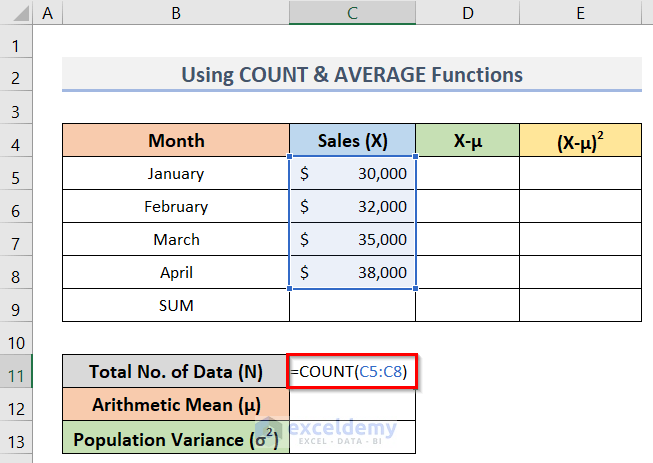
- After that, to calculate the total number of data use the following formula in cell C11:
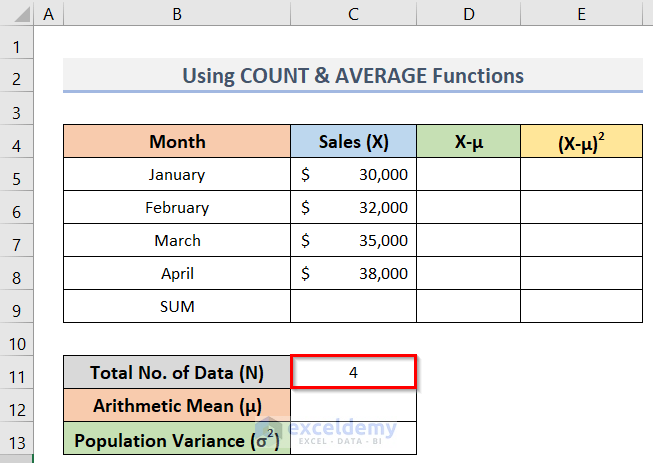
=COUNT(C5:C8)- Press Enter.
- Hence, the resultant value in cell C11 will be N for the above formula of the population variance.
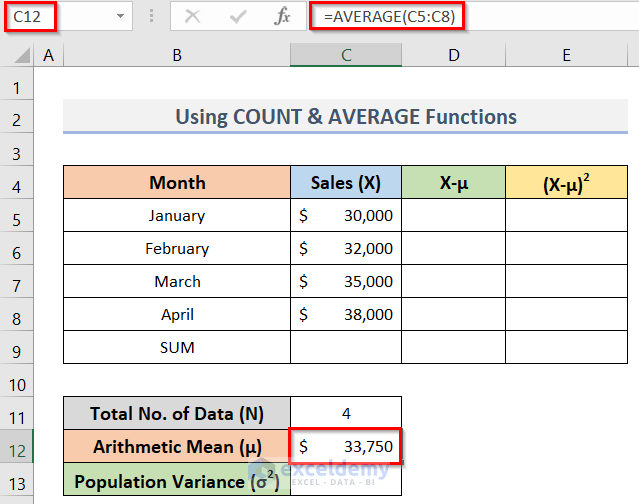
- Afterward, to calculate the arithmetic mean for the individual values type the following formula in the cell C12:
=AVERAGE(C5:C8)- After inserting the formula, press Enter to get the result (see the screenshot below).
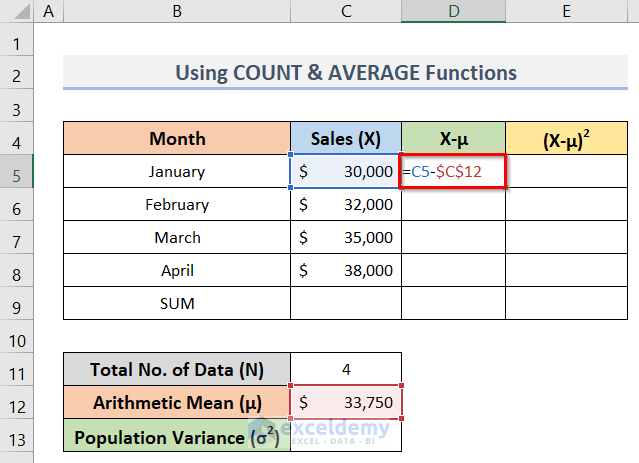
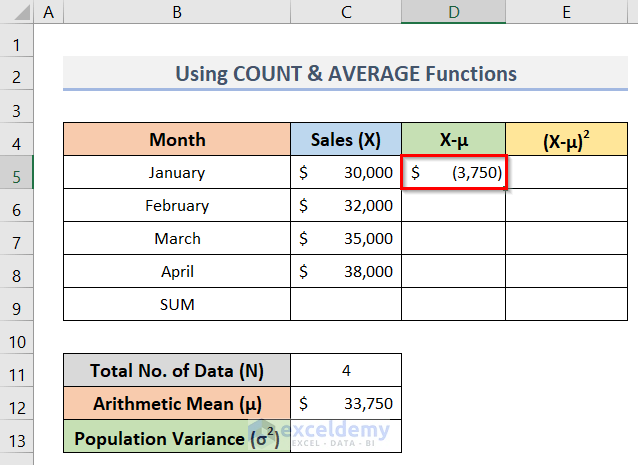
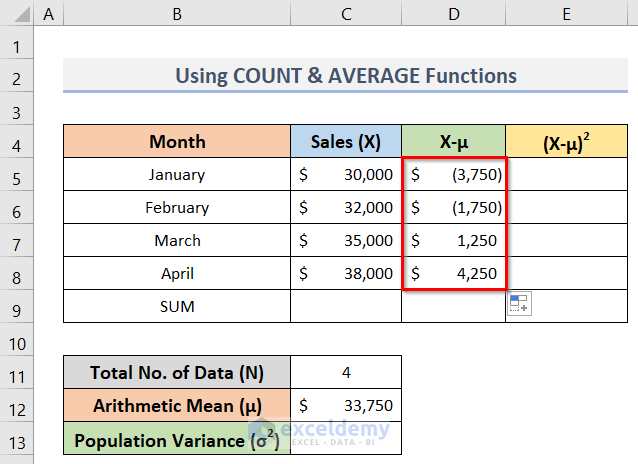
- Eventually, to calculate the deviation about the mean (X-μ), enter the formula below in cell D5:
=C5-$C$12- Press the Enter key to find the result.
- Thereupon, drag the Fill Handle to copy the formula up to cell D8.
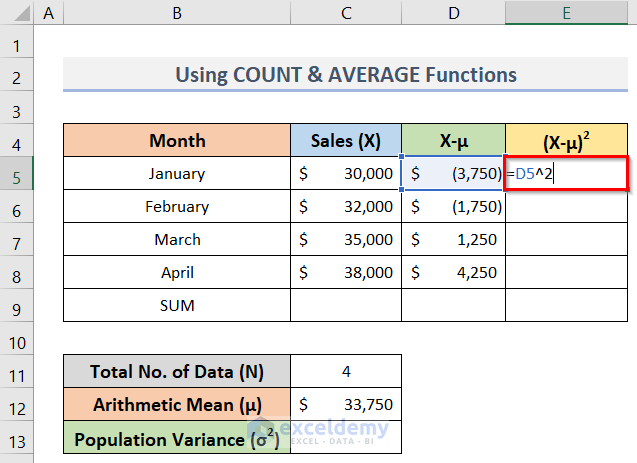
- Subsequently, to square the deviation about the mean (X-μ), assign the following formula in cell E5:
=D5^2- Then, press Enter.
- Therefore, drag the Fill Handle up to cell E8 to copy the formula (see screenshot).
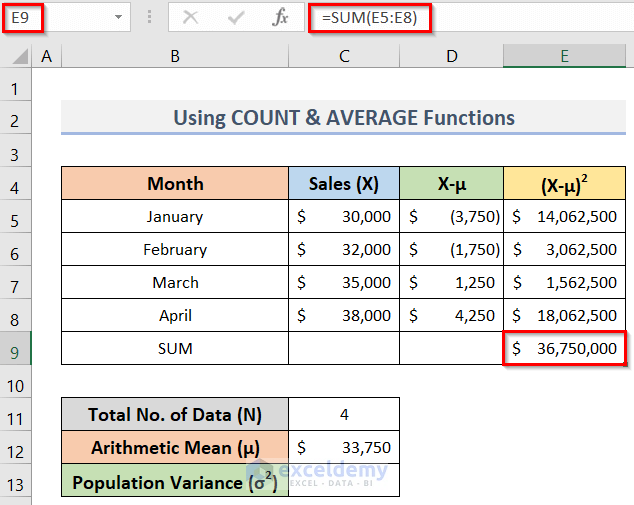
- Next, calculate the sum of the square of the deviation about the mean (X-μ)2 using the formula below in cell E9:
=SUM(E5:E8)- Press the Enter key after entering the formula to get the summation.
- See screenshot.
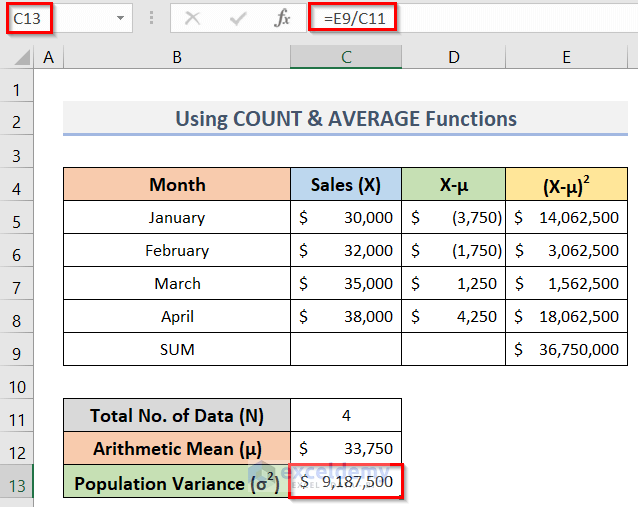
- Finally, calculate the population variance by dividing the square of the deviation about the mean (X-μ)2 by the total number of data (N).
- To do so, type the formula below in cell C13:
=E9/C11- Lastly, press the Enter key and see the desired output in the screenshot below.
2.2 Use Built-in Excel Functions
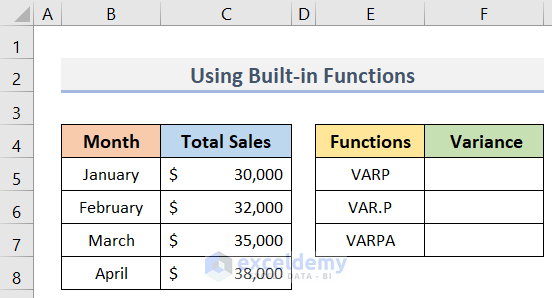
Assuming, we have a dataset (B4:C8) in Excel containing the Total Sales of some months. Here, we will use 3 built-in Excel functions to calculate the population variance of the sales. The functions are the VARP function, the VAR.P function & the VARPA function. The use of these functions to calculate the population variance is below.
VARP Function
First, we will use the VARP function to find the variance. The VARP function is a built-in Excel function that can calculate the population variance at once. The steps for finding the population variance are below.
Steps:
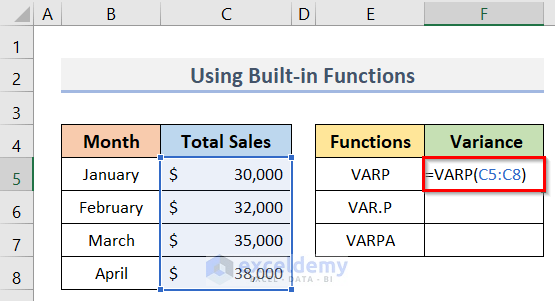
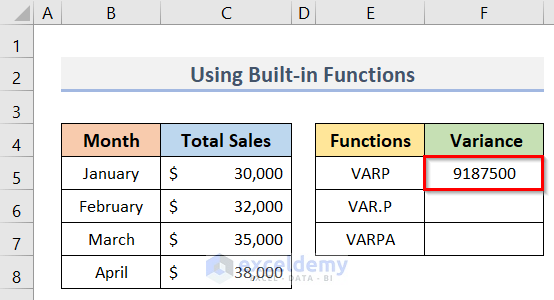
- To begin, go to cell F5.
- Now, to get the population variance of the Total Sales, type the following formula in cell F5:
=VARP(C5:C8)- After that, press the Enter key.
- As a result, we will get the desired population variance in cell F5 (see screenshot).
VAR.P Function
Secondly, we will use the VAR.P built-in function in Excel to determine the variance. This function gives the variance from a whole population. In the VAR.P function, the logical and text values are ignored. See the steps below:
Steps:
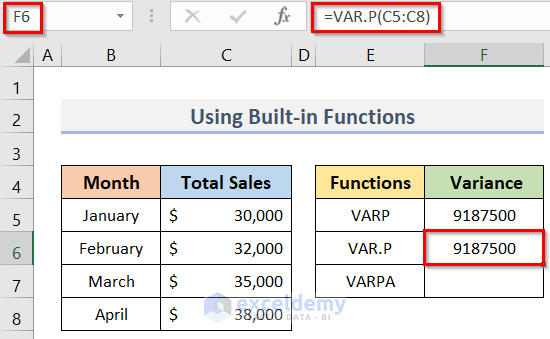
- In the first place, select cell F6.
- Next, calculate the population variance using the formula below in the selected cell:
=VAR.P(C5:C8)- Finally, press the Enter key and then you will see the result in cell F6 of the screenshot below.
VARPA Function
Here, we will use the VARPA function for calculating the population variance. This function evaluates the logical and text values in the calculation. The steps to apply this function are below.
Steps:
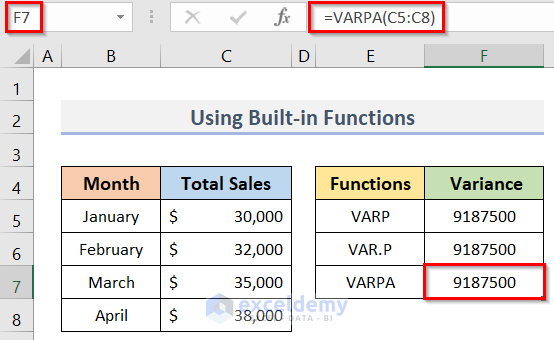
- First of all, activate cell F7.
- Eventually, to get the population variance, type the following formula in the selected cell (F7):
=VARPA(C5:C8)- After inserting the formula, press the Enter key.
- See the final output in the picture below.
Read More: How to Calculate Coefficient of Variance in Excel
3. Determine Excel Sample Variance
In this method, we will learn to calculate the sample variance in Excel. Here, we will apply two approaches to do so. They are: applying manual calculation and then calculation with built-in Excel functions. The approaches are described below.
3.1 Calculate Manually
For calculating the sample variance manually, the following formula is used:
Here,
- μ is the arithmetic mean.
- X is the individual value.
- N is the size of the population.
- σ2 is the sample variance.
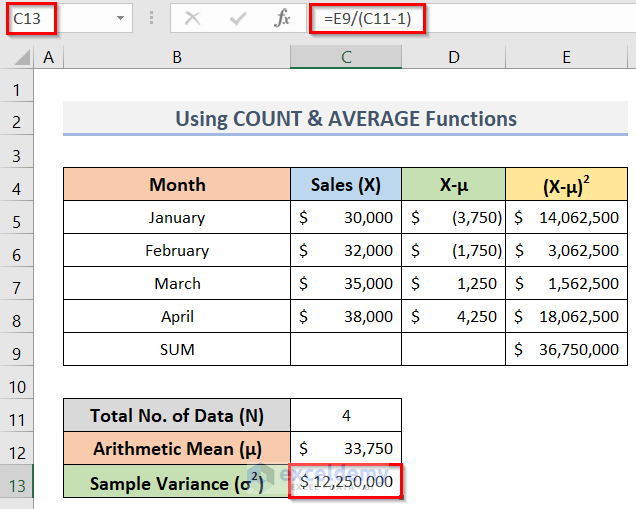
Here, we will use the same dataset that was used for calculating the population variance manually in method 2.1. As you can see, there is only one difference between the previous formula (population variance) and this. It is that the sample formula has a denominator of N-1. But previously the denominator was N. The whole calculation in Excel will be the same. The only difference will be dividing the square of the deviation about the mean (X-μ)2 by (N-1) instead of N. So, with the same values of data, the sample variance is always greater than the population variance. The following picture shows the result (in cell C13) and the necessary data table for the calculation of sample variance. In this case, we inserted the following formula in cell C13:
=E9/(C11-1)Read More: How to Calculate Pooled Variance in Excel
3.2 Assign Built-in Excel Functions
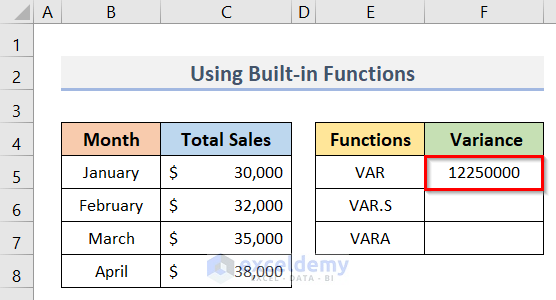
We will now calculate the sample variance using three built-in Excel functions. The three functions are the VAR function, the VAR.S function and the VARA function. To illustrate this method, we will use the Excel dataset (B4:C8) below that contains the Total Sales of the corresponding months. The use of functions for finding the sample variance is below.
VAR Function
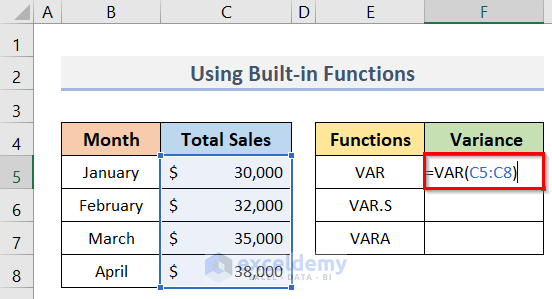
The VAR function is the earliest built-in function in Excel to evaluate variance from a sample. All Excel versions from 2000 through 2019 include this function. The steps to apply this function are below.
Steps:
- To begin, select cell F5.
- Then, to calculate the sample variance, type the formula:
=VAR(C5:C8)- Finally, press the Enter key.
- Thus, we can get the desired sample variance.
- See the result in cell F5 of the following picture.
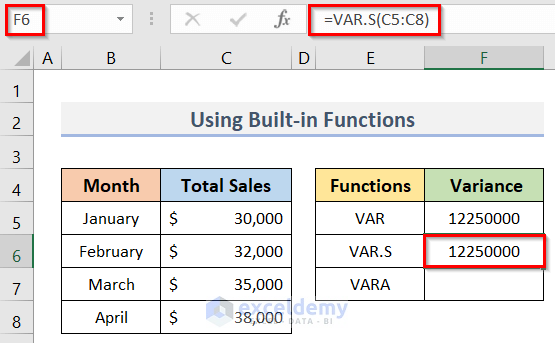
VAR.S Function
The VAR.S function is the updated version of the VAR function in Excel. In the newer versions of Excel, we can apply this function to determine the sample variance. In the following screenshot, we have calculated the sample variance using the VAR.S function.
Steps:
- For determining the sample variance, we entered the formula below in cell F6:
=VAR.S(C5:C8)- Then, we pressed the Enter key.
- Thus, we got the result in cell F6 of the screenshot below.
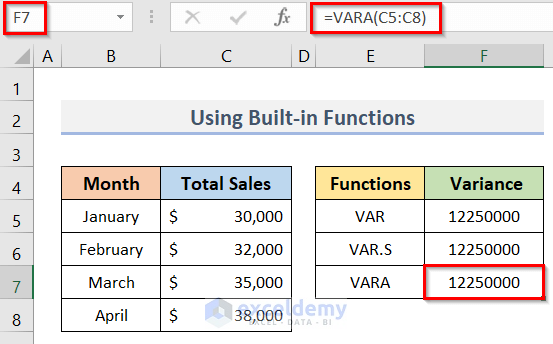
VARA Function
This function calculates the sample variance from a list of numbers and logical text values.
Steps:
- To calculate the sample variance of the dataset below we typed the following formula in cell F7:
=VARA(C5:C8)- After typing the formula, we pressed the Enter key.
- In this way, we can calculate the sample variance (see screenshot).
Things to Remember
Before using the built-in Excel functions to evaluate variance in Excel, there are several factors to consider. Some of them are given below:
- For population data sets, the more recent function, VAR.P, should be used instead of VARP.
- Similarly, for calculating sample variance, VAR.S should be used in the first case, even if VAR and VAR.S are functionally equivalent.
- If you include a text string as a value in a variance formula, you must refer to it in another cell.
Download Practice Workbook
Download the practice workbook from here.
Conclusion
I hope this article will be helpful for you to calculate variance in Excel. Download the practice workbook and give it a try. Let us know your feedback in the comment section.
Calculate Variance in Excel: Knowledge Hub
- How to Calculate Mean Variance and Standard Deviation in Excel
- How to Find the Variance of a Probability Distribution in Excel
- How to Apply Variance Formula in Excel to Get Plus-Minus Results
- How to Calculate Semi Variance in Excel
- How to Calculate Budget Variance in Excel
- How to Calculate Variance of Stock Returns in Excel
- How to Do Price Volume Variance Analysis in Excel
- How to Calculate Schedule Variance Using Excel Formula
- Budget vs Actual Variance Formula in Excel
- How to Calculate Variance Inflation Factor in Excel
- How to Calculate Portfolio Variance in Excel
- How to Create Minimum Variance Portfolio in Excel
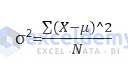
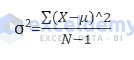



the formula you have for How to Calculate Percentage Variance in Excel is written Variance = ABS(new value-original value)/original value. But in the example is ABS(new value-original value)/new value. so what is it?
Hi Pete, you are right!
Variance= ABS(new value-original value)/original valueis the correct one.We are really grateful for your precious feedback. We have updated the Excel file and main content accordingly.
Best Regards.
-ExcelDemy team.