How to Create Minimum Variance Portfolio in Excel (2 Examples)

The article will show you how to create a Minimum Variance Portfolio in Excel. A properly organized portfolio with individual risky properties or assets that are combined when traded together creates a Minimum Variance Portfolio. This portfolio gives an efficient idea to an investor how much money he can invest to a company with the lowest possible risk. We also need the rate of change in stock for that. Let’s stick to the following sections of this article to find out how we can create a Minimum Variance Portfolio using Excel.

What Is Minimum Variance Portfolio?

The Minimum Variance Portfolio hedges the total portfolio risk for the level of risk allowed in relation to the anticipated rate of return on the portfolio by leveraging the risk of each individual asset with an offsetting investment. Simply said, each investment in a minimum variance portfolio is dangerous if traded separately, but the risk is compensated when exchanged as a portfolio. The Markowitz Portfolio Theory, which contends that volatility can be used to substitute risk and that lower volatility variance is correlated with lower investment risk, is where the word first appeared.

How to Create Minimum Variance Portfolio in Excel: 2 Practical Examples

In this article, I’ll show you two examples of how to create a Minimum Variance Portfolio in Excel. We will use two different datasets. Here, I’ll present to you a set of Stock Return data of five large companies for 10 months. This data refers to the rate of change in stock each month. Following this data, an investor can have an idea of what percentage of investment in any of these companies will be risk free. Let’s have a look at the data.

1. Using Matrix to Create Minimum Variance Portfolio (Multi Assets)

As you can see, we have five different companies’ stock return data in our Excel sheet, so it will be good for us to use a matrix to model the Minimum Variance Portfolio. This approach is really useful if you have stock return data of more than two companies or assets. Let’s go through the procedure below.

Steps:

First, we need to calculate the Excess Returns of these companies. For that reason, we go to a new sheet and use a formula to calculate it.
After that, type the following formula in B6 and press ENTER. This will show you the Excess Return of Microsoft for the first month.

=dataset!B5-AVERAGE(dataset!B$5:B$14)

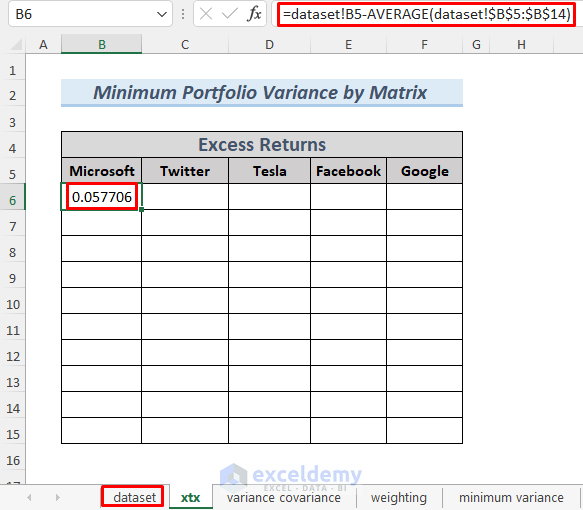
The formula uses the AVERAGE function to calculate the average of total stock returns Microsoft. Then it is subtracted from each stock return to get the Excess Return data. The dataset term in the formula means that the cell reference is coming from the dataset sheet.

Next, drag the Fill Handle to the right to AutoFill the cells to F6.

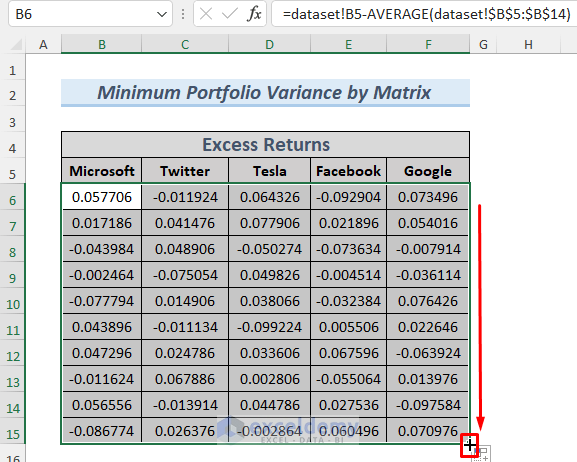
Thereafter, use the Fill Handle again to AutoFill all the cells. This command will return all the Excess Returns for 10 months.

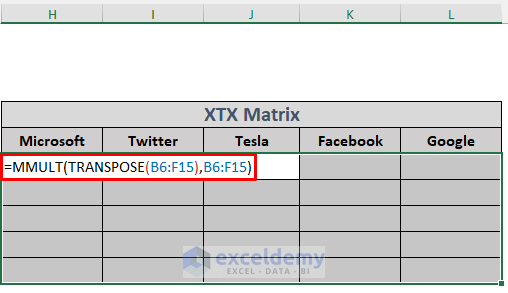
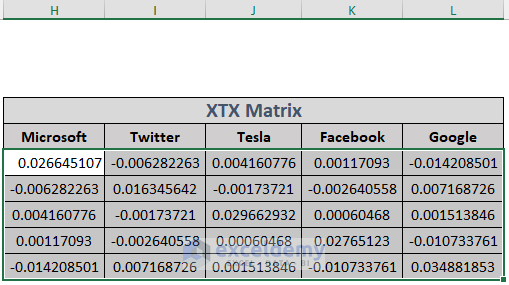
Next, we will create a matrix by multiplying the transpose of the array B6:F15 with the B6:F15 We will use this matrix to determine the variance in the future. For that purpose, create some columns to store the data of the matrix, select the 5×5 (multiplication between 5×10 and 10×5 matrices will result in a 5×5 matrix) range (H6:L10), and type the following formula in H6.

=MMULT(TRANSPOSE(B6:F15),B6:F15)

The formula uses the TRANSPOSE function to transpose the array B6:F15. The MMULT function returns the matrix multiplication result between this transposed array and B6:F15.

After that, hold CTRL+SHIFT and press ENTER. Although it won’t give you any errors in the latest version of Excel, you get errors in the older version of Excel. You will see the output of the Matrix Multiplication in the sheet.

We will go to another new sheet for our convenience. Create necessary columns in it as well.
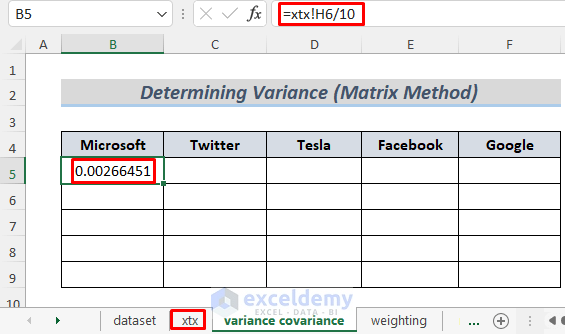
After that, type the following formula in B5.

=xtx!H6/10

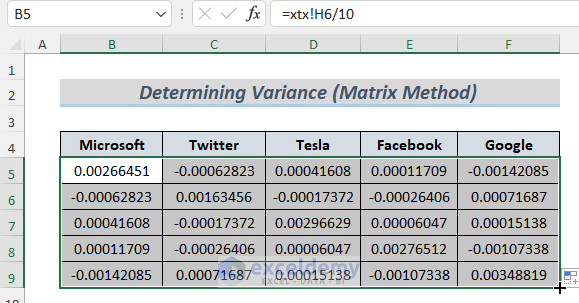
Later, drag the Fill Icon to the right upto F5. After that, also drag down the Fill Icon to AutoFill the lower cells. This will create a Portfolio Return Matrix.

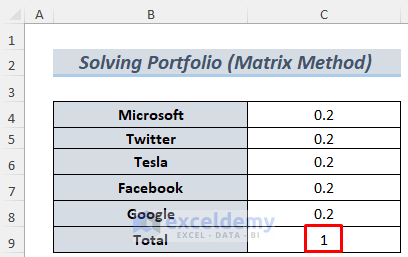
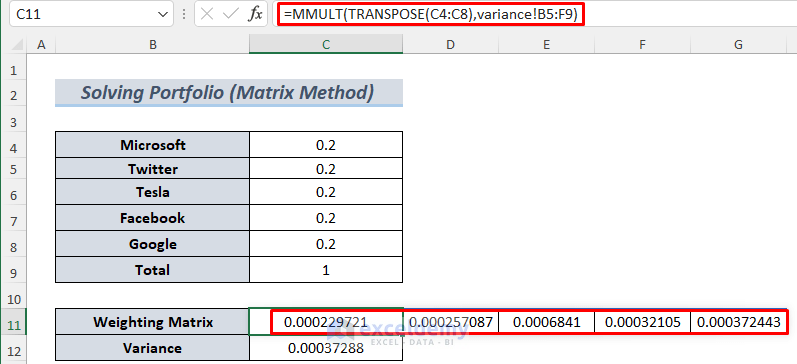
Thereafter, we will use some dummy data to solve our Portfolio. Select five decimal numbers that total to 1. If you have 6 companies, you should select 6 decimal numbers. Here, I just chose 2 as 0.2 times 5 equals 1. This is the hypothetical investment percentage for an investor.

After that, type the following formula in C11 to determine the Weighting Matrix. Make sure you select the array C11:G11 and hold CTRL+SHIFT before pressing ENTER. Although it won’t give you any errors in the latest version of Excel, you get errors in the older version of Excel.

=MMULT(TRANSPOSE(C4:C8),variance!B5:F9)

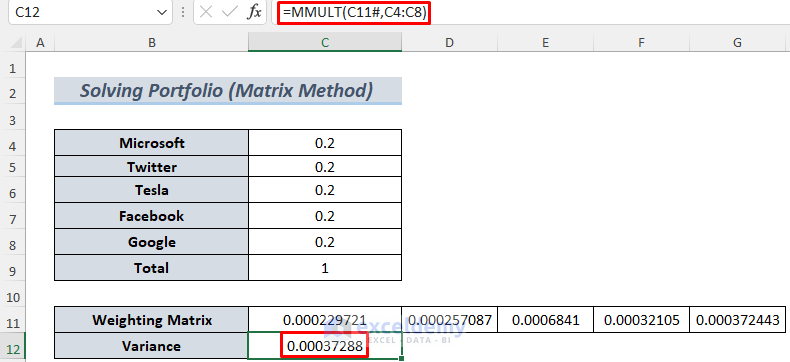
Similarly, use the following formula to determine the Variance of our data.

=MMULT(C11#,C4:C8)

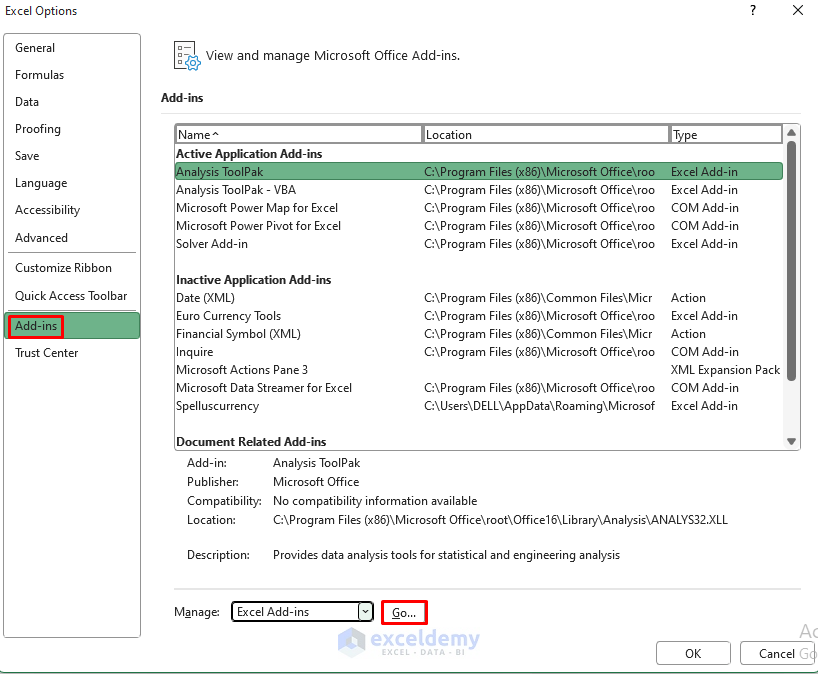
We are almost there. Just we need to use the Solver Toolpak to finish our job. If you don’t have this in your Data Tab, you need to go to the File Menu >> Options >> Add-ins >> Manage >> Excel Add-ins >> Go…

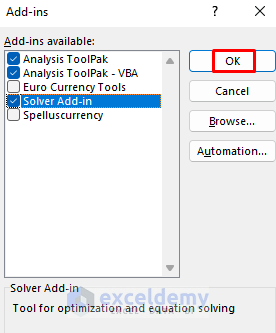
After that, the Add-ins window will appear. Check Solver Add-in and click OK.

The Solver Add-in will appear in the Data Tab. Click on it to open it.

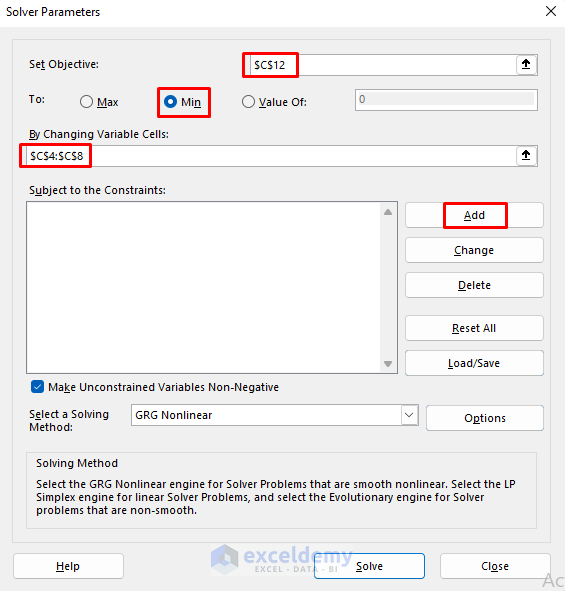
Next, you need to insert Solver Parameters. Here, we need to minimize the risk by minimizing the variance. So our Objective cell will be C12 which stores the value of Variance. Also, select Min.
After that, select C4:C8 for Changing Variable Cells. We will get the percentages of sustainable investment in these cells once we launch the Solver.
In addition, we will add some Constraints to get more accurate results.

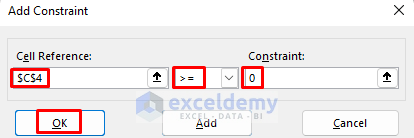
After clicking on Add, the Add Constraint dialog box will show up. Here I set the value of cell C4 to greater or equal to zero.

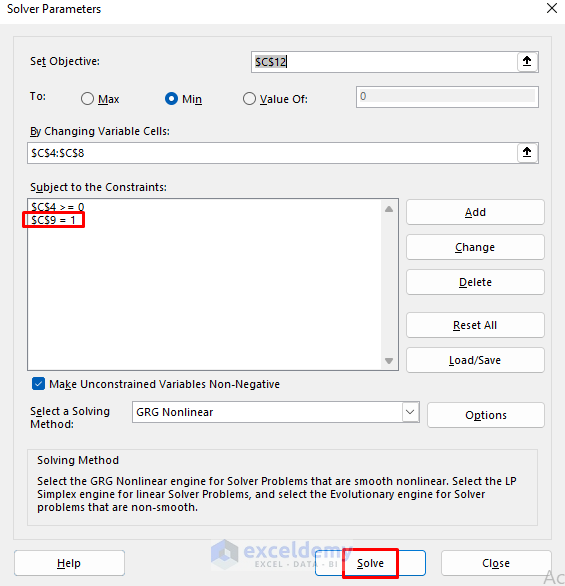
Similarly, I added another constraint which sets the value in C9 to 1.
After that, let’s click on Solve.

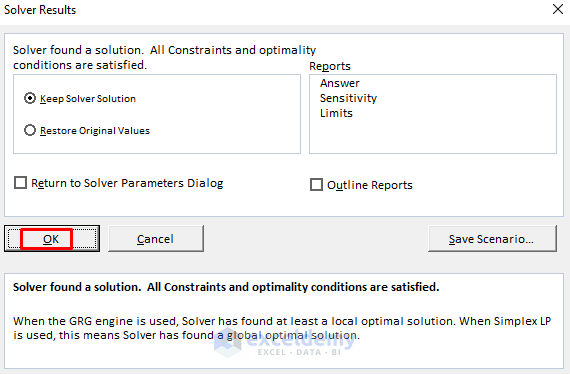
The Solver Results window will appear. Just click OK.

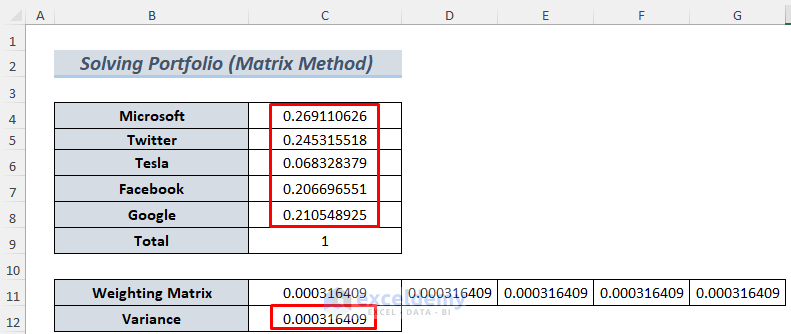
Next, you will see the minimized Variance and the risk-free investment percentage.

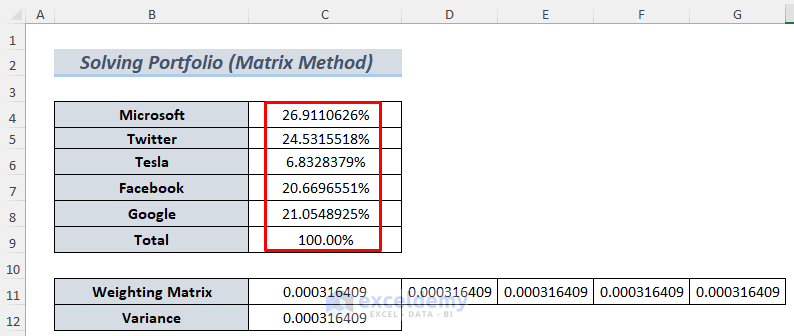
Let’s convert these decimals to percentages. The output illustrates that 9110626% of investment in Microsoft, 24.5315518% of investment in Twitter, and so on will be risk-free for an investor.

Thus you can create a Minimum Variance Portfolio in Excel.

2. Minimum Variance Portfolio Comparing Two Assets

Here, I’ll show you how to calculate Minimum Variance Portfolio when you have two companies or assets in your consideration. This is a less complex method than the previous one. Let’s stick to the process for a better understanding.

Steps:

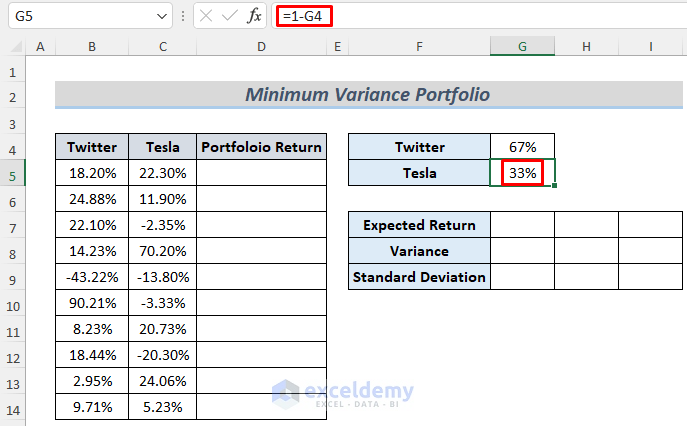
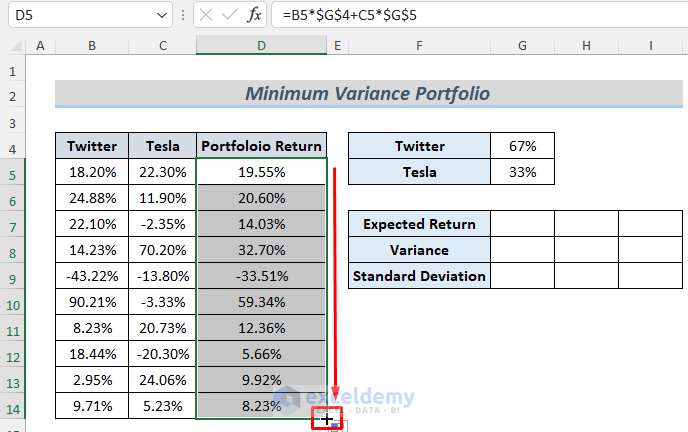
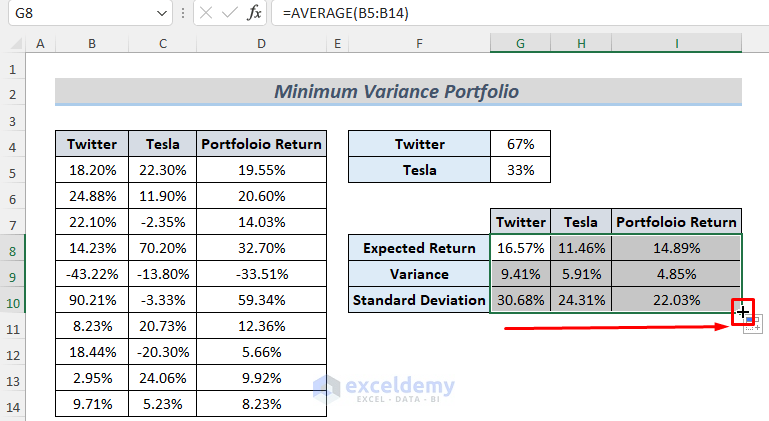
First, insert the stock return data and select some cells to store the necessary data like Standard Deviation or Variance. Set an initial investment percentage. Say, we want to invest 67% in Twitter. The rest will be invested in Tesla.
For that reason, type the following formula in G5.

=1-G4

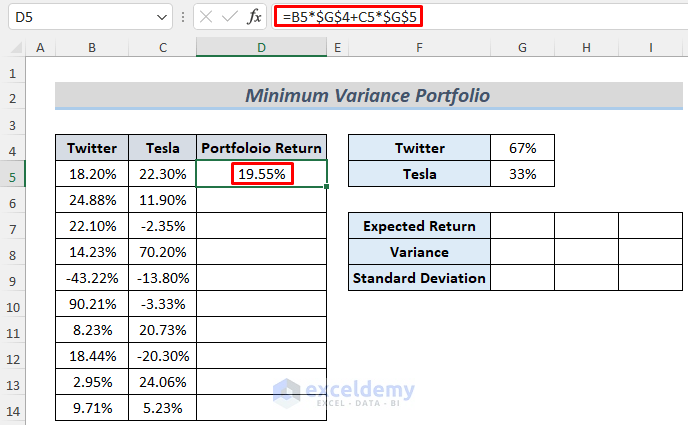
Thereafter, type the following formula in cell D5 which will return the Portfolio Return

=B5*$G$4+C5*$G$5

Later, use the Fill Handle to AutoFill the lower cells.

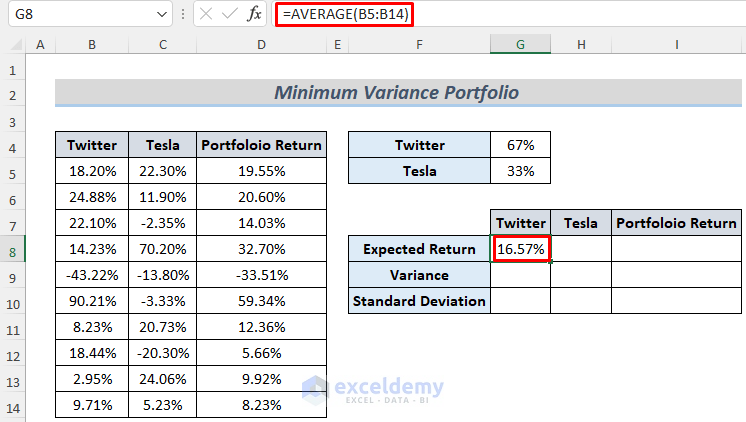
Again, we use another formula to calculate Expected Returns for Twitter, Tesla, and Portfolio Return.

=AVERAGE(B5:B14)

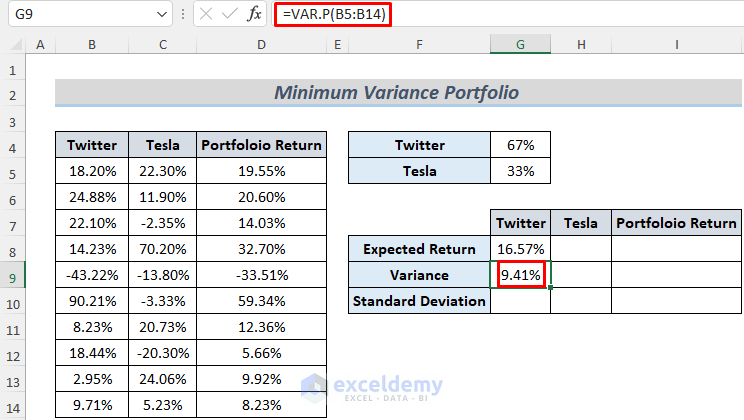
Next, we will use the VAR.P function to calculate the variance of stock returns of Twitter. We want to ignore any logical values and text in the data, so we used the P function.

=VAR.P(B5:B14)

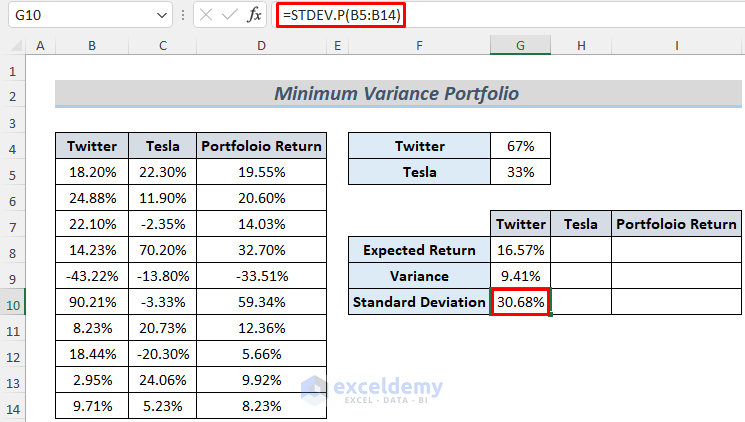
Thereafter, type the following formula to calculate Standard Deviation using the STDEV.P function.

=STDEV.P(B5:B14)

Drag the Fill Icon to the right to determine the Expected Return, Variance and Standard Deviation for other data.

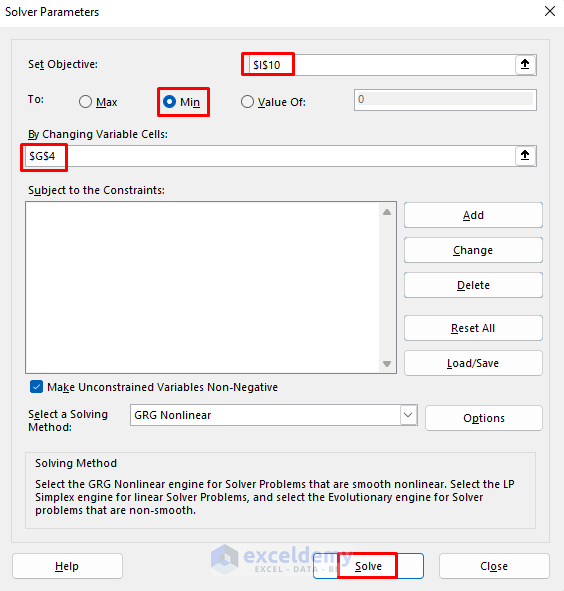
Again, we want to Minimize the Variance or Standard Deviation (as Standard Deviation is simply the square root of Variance, we can use any of them for the Minimum Variance Portfolio).
So, we insert the cell reference I10 where the Portfolio Return Standard Deviation is stored and set the Objective to Min.
We will see the change by varying the investment percentage of Twitter. So we insert the G4 cell reference in the ‘By Changing Variable Cells’ section.
Later, just click on Solve.

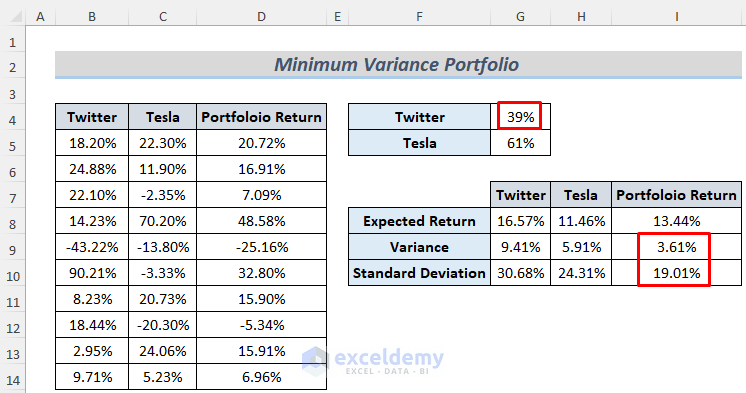
After that, we will get the optimum value for the investment percentage in both Twitter and Tesla. Also, we minimize the Variance from 85% to 3.61%.

This is another efficient and easy method to create a Minimum Variance Portfolio in Excel.

Download Practice Workbook

Minimum Variance Portfolio.xlsx

Conclusion

In the end, we can conclude that you will learn how to create a Minimum Variance Portfolio in Excel after reading this article. If you have any better suggestions or questions or feedback regarding this article, please share them in the comment box. This will help me enrich my upcoming articles.

<< Go Back to Calculate Variance in Excel | Excel for Statistics | Learn Excel

Get FREE Advanced Excel Exercises with Solutions!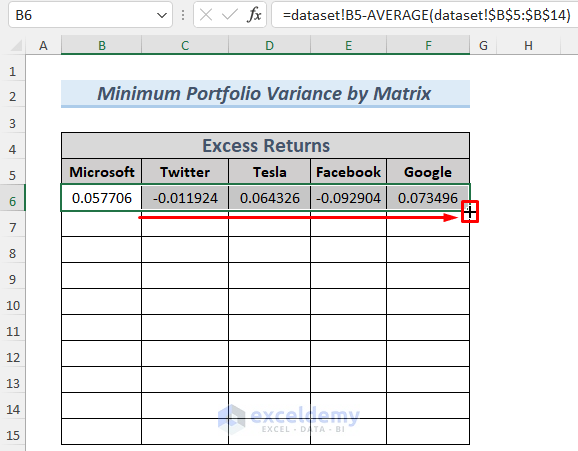

1 Comment

Brenton Nov 18, 2022 at 4:58 AM

=dataset!B5-AVERAGE(dataset!$B$5:$B$14)

should be

=dataset!B5-AVERAGE(dataset!B$5:B$14)

otherwise when you copy across to the other stocks, you are still using the Average for Microsoft to calculate the excess returns of the other stocks