Excel Student Loan Amortization Schedule [Free Download]

Excel student loan amortization schedule is an Excel amortization schedule that helps students to track and visualize their student loan repayment process. From this table, the borrower students would be able to know their required regular payments and how the payments affect the principal paid, interest paid, and remaining balance amount after each payment.

Download our free “Excel Student Loan Amortization Schedule” template to generate your own student loan amortization schedule and read the article to learn how to use this template efficiently.

This template would be greatly helpful and effective for students who are looking forward to going to college or university with fewer funds available.

Click here to enlarge the image

Download Excel Template

For: Excel 2007 or later
License: Private Use

⏷What Is Student Loan?
⏷Student Loan Amortization Schedule Excel Template
  ⏵Basic Student Loan Amortization Schedule
  ⏵Student Loan Amortization Schedule with Extra Payments (Regular/Irregular)
  ⏵Student Loan Amortization Schedule with Grace Period
⏷Student Loan Amortization Schedule Excel Template Tips
⏷Student Loan FAQs

What Is Student Loan?

A student loan is basically a loan that is taken by the students to use for their studies. They can use it for their tuition fees, books, or any other educational expenses. They can take it from the federal government, state government, or any private institution.

Generally, student loan is given for 10 years and it is mainly given at a fixed interest rate. Some student loans might have some grace periods of 6 months whereas some other student loans might not have. Besides, students can apply for both subsidized and unsubsidized student loans depending on their scholarships, tuition aid, and available funds.

Student Loan Amortization Schedule Excel Template

Depending on the factors and variation of loan types, there are multiple types of student loan amortization schedule. Such as:

1. Basic Student Loan Amortization Schedule: It focuses on the simple and basic student loan amortization table.
2. Student Loan Amortization Schedule with Extra Payments (Regular/Irregular): To pay off the loan quicker and pay lesser interest, a student might make several extra payments (regular/irregular). This template would provide you the necessary input fields and outputs for this special feature and a summarized amortization schedule.
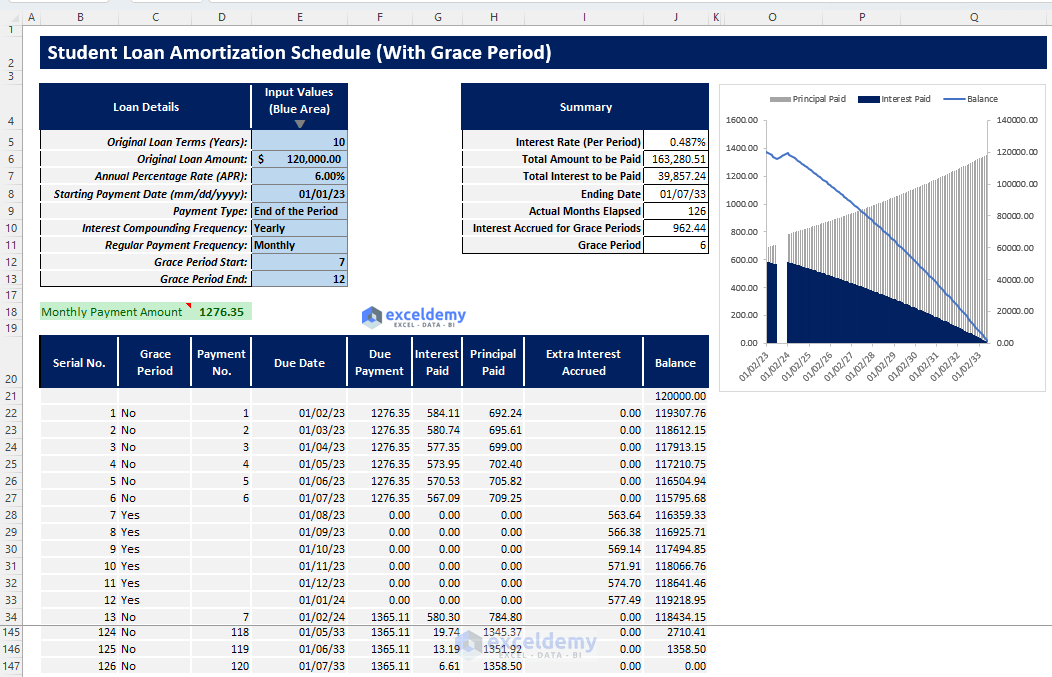
3. Student Loan Amortization Schedule with Grace Period: This template would help students to generate their amortization table if they are approved for some grace periods within their loan terms.

Read More: Amortization Schedule with Irregular Payments in Excel

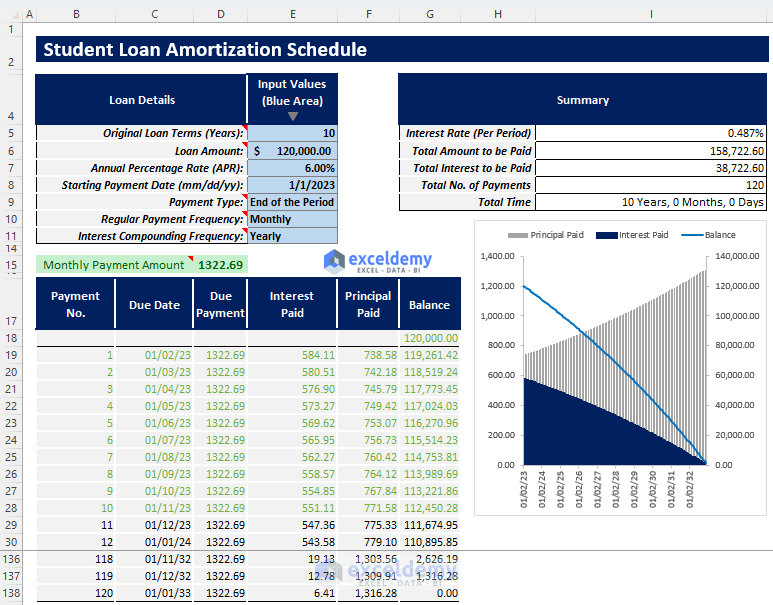
Template 1: Basic Student Loan Amortization Table

This template would take the necessary inputs and give you an automated amortization schedule for your student loan. You will also get a summary output showing you all the important results. Besides, you will get a summary chart displaying the principal paid, interest paid, and remaining balance over the loan tenure.

Click here to enlarge the image

How to Use This Template

To use this template efficiently, follow the instructions below.

Instructions:

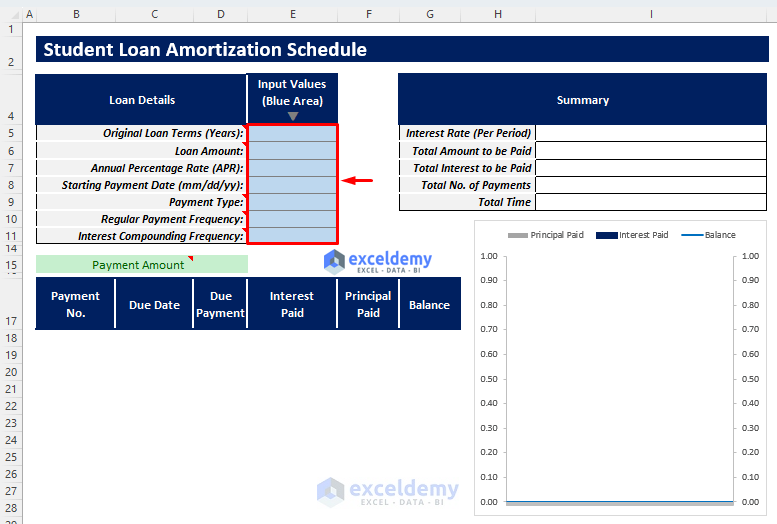
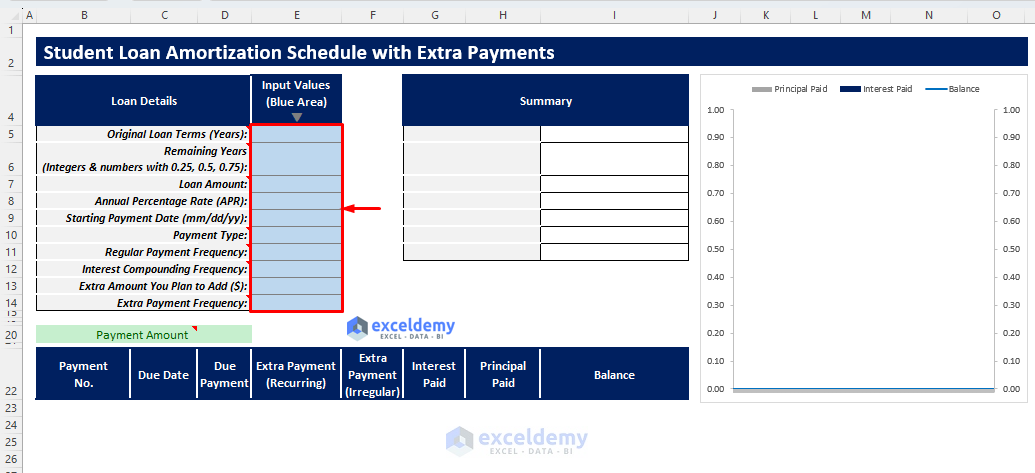
• Insert the required inputs in the blue-shaded area of the Input Values column according to the loan parameters. The necessary inputs are:

1. Original Loan Terms (Years)
2. Loan Amount
3. Annual Percentage Rate (APR)
4. Starting Payment Date
5. Payment Type
6. Regular Payment Frequency
7. Interest Compounding Frequency

Click here to enlarge the image

• After inserting the inputs properly, you will get your required payment amount and automatically generated student loan amortization schedule.
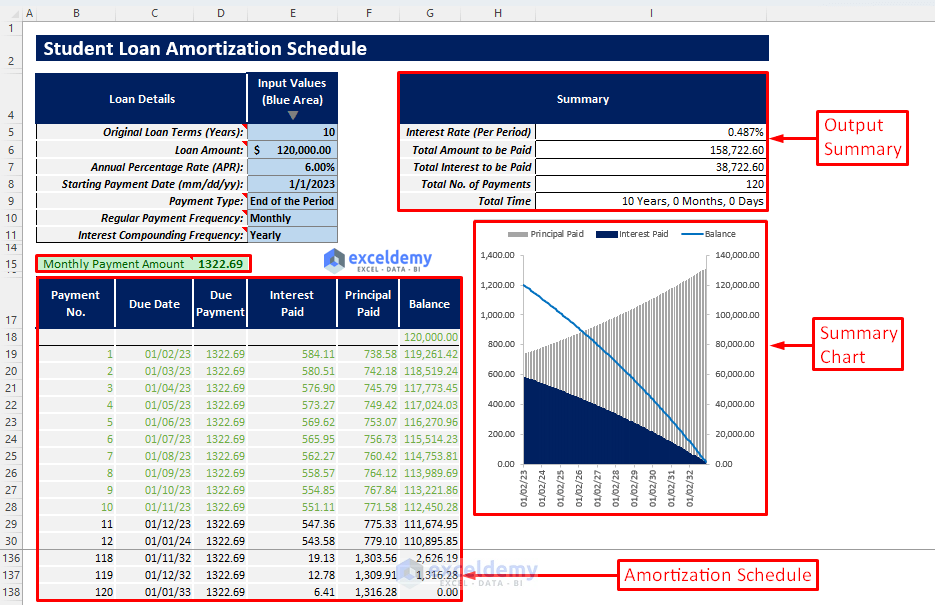
• You will get an output summary containing-

1. Interest rate (Per Period)
2. Total Amount to be Paid
3. Total Interest to be Paid
4. Total No. of Payments
5. Total Time

• You will also get a summary chart showing interest paid, principal paid, and remaining balance trend over the loan tenure.

Click here to enlarge the image

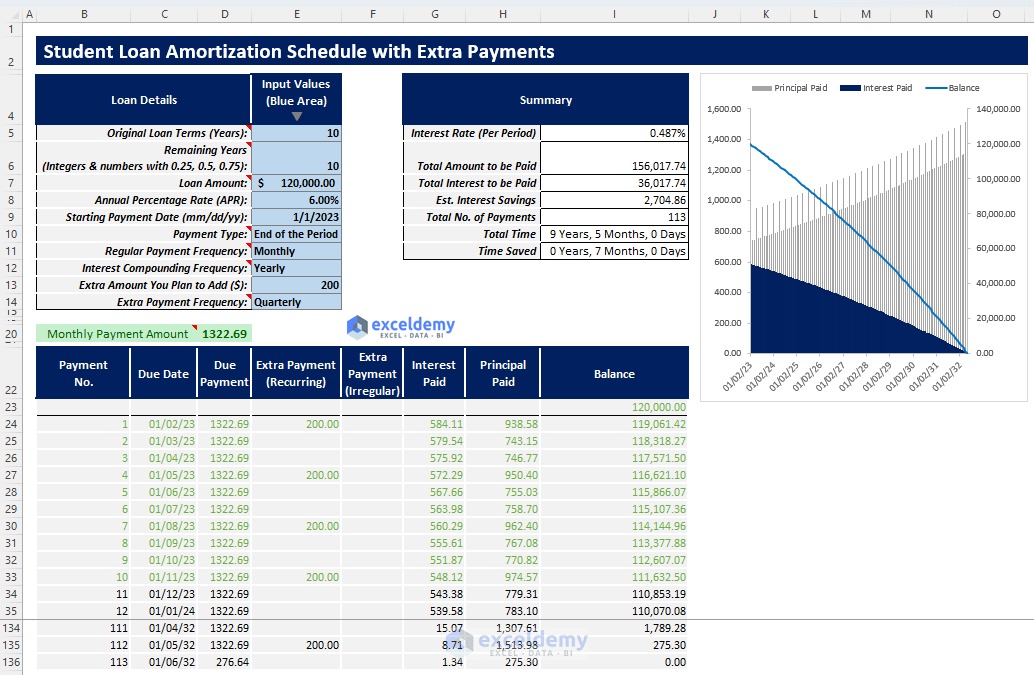
Template 2: Student Loan Amortization Schedule with Extra Payments (Regular/Irregular)

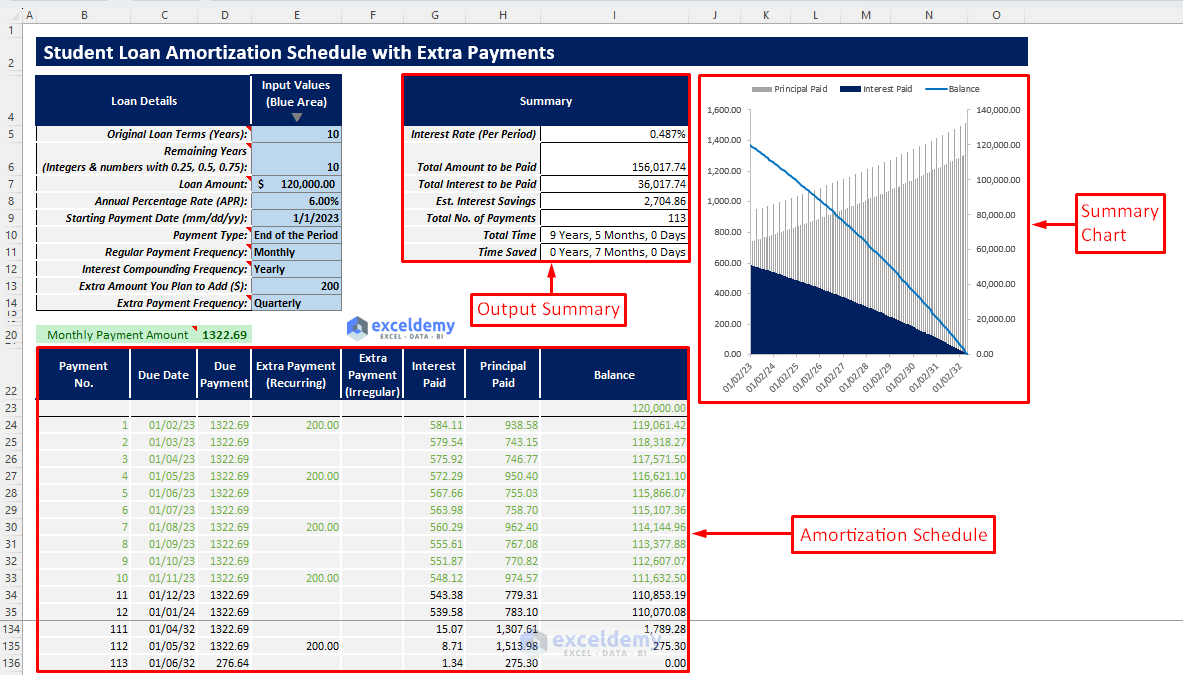
In this template, along with the basic necessary inputs like the previous template, you can also insert extra regular or irregular payment entries. You will get the special amortization schedule and a summary chart automatically after inserting the inputs. You will get an output summary containing all necessary outputs such as Estimated Interest Savings and Time Saved.

Click here to enlarge the image

How to Use This Template

Go through the instructions below to use this template efficiently.

Instructions:

• Insert all the required inputs in the blue shaded area of the Input Values column according to the loan parameters stated in the Loan Details column.

Click here to enlarge the image

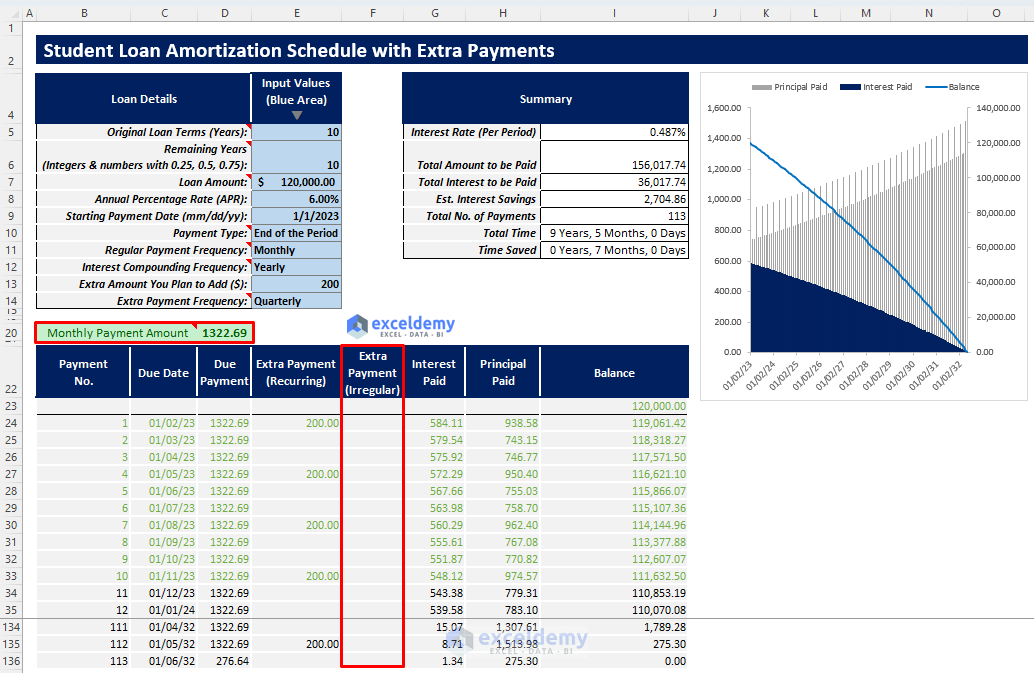
• After inserting the inputs, you will get your required regular payment amount. If you want to make some extra irregular payments, you have to add this in the Extra Payments (Irregular) column.

Click here to enlarge the image

• You will get your finalized student loan amortization schedule along with an output summary and a summary chart to visualize your results better.

Click here to enlarge the image

Read More: Amortization Schedule Excel Template with Extra Payments

Template 3: Student Loan Amortization Schedule with Grace Period

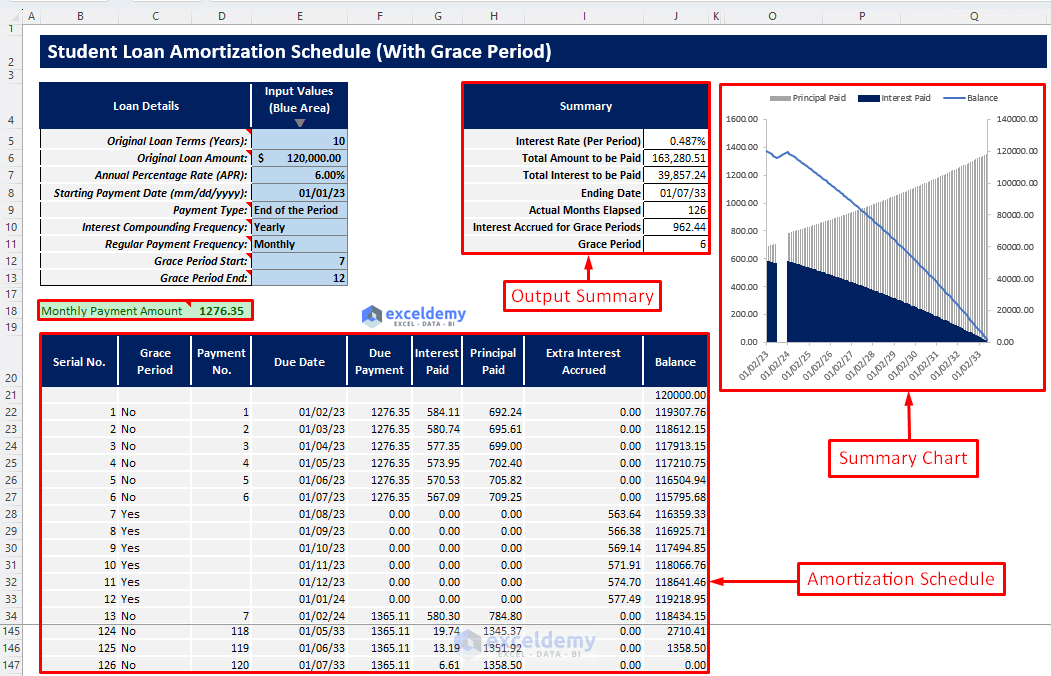
In this template, you will be able to utilize the grace period feature of loan. After inserting proper inputs and choosing your grace period range, you will be able to get your student loan amortization schedule with a grace period. You will also get an output summary and a summary chart.

Click here to enlarge the image

How to Use This Template

Follow the instructions below to use this template properly.

Instructions:

• Go to the “Payoff with Grace Period” sheet.
• Insert all required inputs along with Grace Period Start and Grace Period End in the blue shaded area of the Input Values column.

Click here to enlarge the image

• After inserting the required inputs, you will get your required payment amount for your student loan and you will get an output summary containing necessary outputs such as Interest Accrued for Grace Periods, Grace Period and Actual Months Elapsed, etc.
• You will get a summary chart to visualize your interest paid, principal paid, and remaining loan balance trend over the loan term.

Click here to enlarge the image

Read More: Multiple Loan Amortization Schedule Excel Template

Student Loan Amortization Schedule Excel Template Tips

• When inserting the inputs and choosing the dropdowns, it is highly recommended that you read the notes given in the loan parameters. Otherwise, errors might occur for inserting wrong inputs or choosing wrong dropdowns.
• When choosing interest compounding frequency, keep in mind that, interest compounding frequency has to be equal to or greater than your chosen regular monthly payment frequency.
• When choosing the extra payment frequency, choose it as a multiple of your chosen regular payment frequency. Otherwise, an error might occur.

Student Loan FAQs

1. What Are Subsidized and Unsubsidized Student Loans?

Subsidized loans are basically federal loans given to students where the students do not have to pay interest in their school or college years, rather they start to repay their actual loan after their graduation. But, in unsubsidized loans, interest starts to accrue and accumulate with actual loans until the students start to repay their loans.

2. What Are Federal and Private Loans?

Federal loans are the loans mainly given by the federal government whereas private loans are the loans that are given by private institutions or banks. Generally, federal loans have a lesser interest rate than private loans. And, federal loans can be subsidized or unsubsidized. But, private loans are always unsubsidized.

3. What Is Grace Period for Student Loans?

Grace periods are the periods in which the borrower is not obliged to pay his regular payment. S/he will not be penalized for not paying in these periods. However, interest on the remaining balance might accrue in these periods depending on the type of loan.

4. Can Someone Repay a Student Loan Through a Credit Card and Does it Affect the Credit Score?

Generally, federal loans can’t be paid with a credit card. However private loans can be paid through credit cards most of the time. But, this may not be a good idea as this will result in extra charges and fees. And, yes, paying regularly always improves your credit score.

Related Articles

• Preparing Bond Amortization Schedule in Excel
• Excel Interest Only Amortization Schedule with Balloon Payment Calculator
• Amortization Schedule with Balloon Payment and Extra Payments in Excel
• ARM Amortization Schedule Excel Template 
• Excel Car Loan Amortization Schedule Template
• Excel Car Loan Amortization Schedule with Extra Payments Template

<< Go Back to Amortization Schedule | Finance Template | Excel Templates