Khan Muhammad Kawser
We will show how to create stock return frequency distributions and histograms in Excel. A histogram is a widely used way to summarize a large data set. Creating a histogram using the Data Analysis ToolPak is very easy. This blog is aimed at showing you how you can use a histogram chart to summarize the returns of a stock. Then we will show you how you can compare the returns of two or more stocks using their histogram charts.
Download Practice Workbook
You can download the Excel file from the link below.
Creating Histogram Using Stock Returns Data
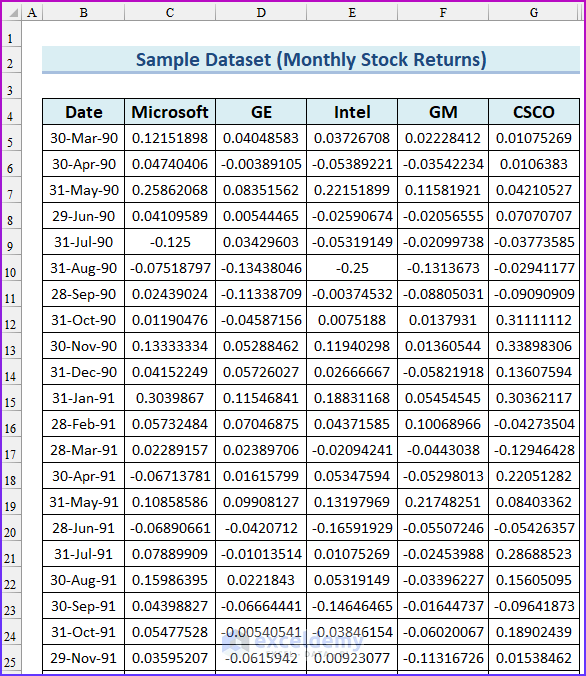
In the image below, you are seeing a total of 4 stocks with their monthly returns. The stocks are Microsoft, General Electric, Intel Corporation, General Motors, and Cisco. The leftmost column shows the last working day of the month, and the date starts on March 30, 1990.
There are a total of 130 data points in a column, from March 30, 1990, to December 29, 2000. A data set with 130 data points is not that large, but it is enough for our analysis. If you want to add more data points for your analysis, you can visit any website that stores daily stock prices.
Before calculating the return on a stock, let’s review the general rules of building a histogram from a large data set.
Read More: How to Get Stock Prices in Excel (3 Easy Methods)
Step-by-Step Procedures to Create Stock Return Frequency Distributions and Histograms in Excel
We’ll walk you through the process of creating frequency distributions and histograms in Excel using Cisco stock return data. Firstly, we will show you how to calculate the frequency distributions in Excel. Lastly, we will create a histogram using the data analysis feature. Moreover, we will discuss the common shapes of histograms in the later part of this article.
Step 1: Calculating Frequency Distributions
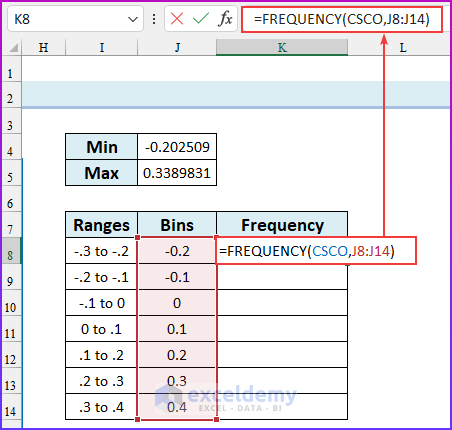
In this first step, we will use the FREQUENCY function to calculate the frequency distributions of the Cisco stock return data in Excel. Additionally, we will also use the MIN and MAX functions to find the minimum and maximum values of that data. Using these values, we will create bins or intervals to group the data. Moreover, we have used the named range “CSCO” for the cell range G5:G134.
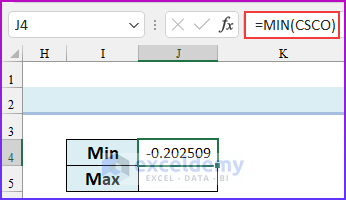
- Firstly, find out the minimum value of the data set by typing this formula in cell J4.
=MIN(CSCO)
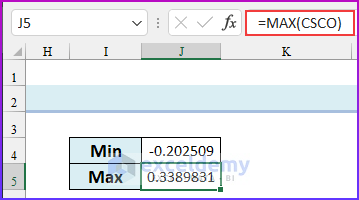
- Secondly, find out the maximum value of the data set by typing the following formula in cell J5.
=MAX(CSCO)
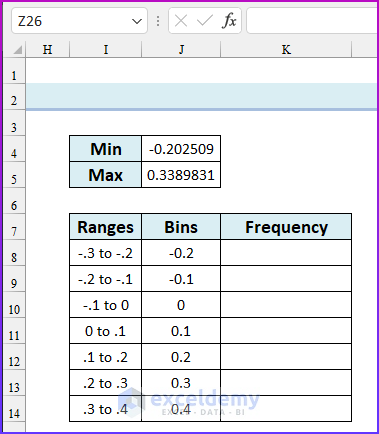
- Now, from these values, we can create bins to calculate the frequency distribution. A standard histogram should have a number of ranges between 8 to 15 (our advice is: to take a total of 10 ranges).
- So, create bins similar to the following image.
- Then, type the following formula in cell K8.
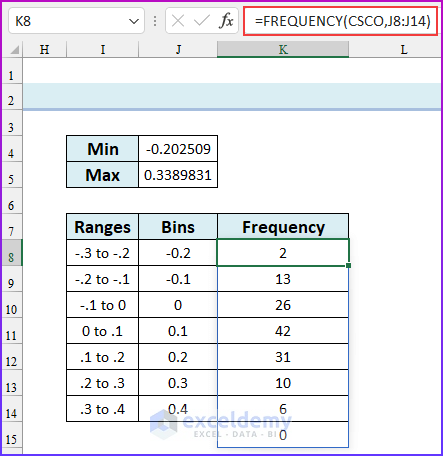
=FREQUENCY(CSCO,J8:J14)
- After that, press ENTER. Remember, this is an array formula and we are using the Microsoft 365 version of Excel, if you are using an older version, then you will need to pre-select the cell range K8:K15, type the formula, and press CTRL+SHIFT+ENTER. Thus, we will finish creating the frequency distribution in Excel.
Step 2: Creating Histograms in Excel
Now, we will make a histogram using our Cisco data. We will use the same bins to create a histogram in this step. Before doing anything, you need to enable the Data Analysis Toolpak in Excel. Additionally, the frequency distribution will be automatically created using the data analysis feature.
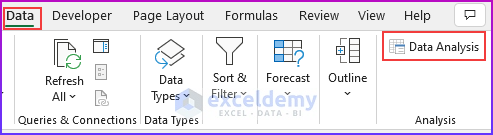
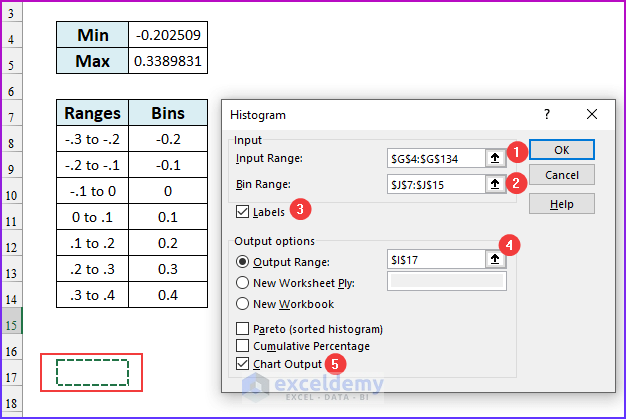
- To begin with, open the Data Analysis dialog box (Data tab → Analysis group of commands → Data Analysis).
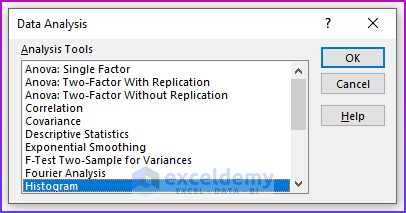
- Then, from the Data Analysis dialog box, choose the Histogram option. A Histogram dialog box will appear.
- Next, in the Input range, insert cell range $G$4:$G$134, in the bin range insert cell range $J$7:$J$15.
- After that, select the checkbox Labels. As our selected input and bin ranges have labels (CSCO & Bins).
- Next, as Output range, we select cell reference: $I$17. And finally, we select the Chart Output checkbox as we want to see the Histogram also on the chart.
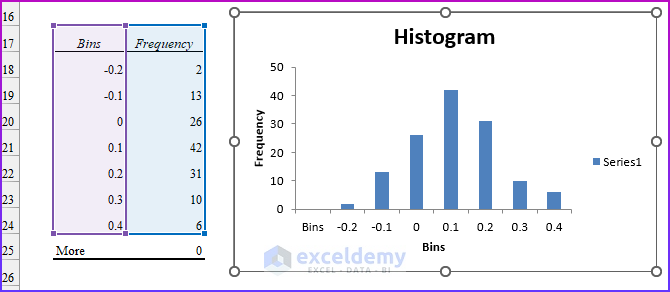
- When done, just click OK. You will get a Histogram table and chart like shown in the image below.
- So, this is our frequency distribution table with the chart output. From the frequency table and from the chart, it is clear that Cisco returns are most likely between 0 and 10 percent per month, and the height of the bars drops off as the graph moves away from the tallest bar. This concludes the creation process of the histogram in Excel.
Read More: How to Get Historical Data of NSE Stocks in Excel (2 Effective Ways)
Similar Readings
- How to Import Stock Prices into Excel from Google Finance (3 Methods)
- Get Stock Quotes in Excel (2 Easy Ways)
- How to Get Current Stock Price of India in Excel
- Download Historical Stock Data into Excel (with Easy Steps)
- How to Track Stock Prices in Excel (2 Simple Methods)
Stock Returns Comparison Using Histograms
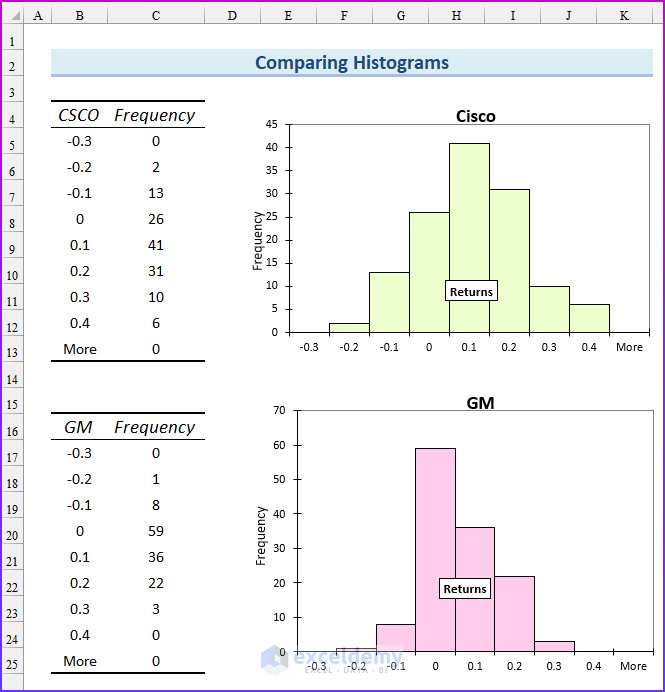
Now, you will see how to use histograms to compare two stocks. Analysts are often asked to compare different datasets. For example, you might be asked how the monthly returns on GM and Cisco stock differ. To answer a question such as this, you can construct a histogram for GM by using the same bin ranges as for Cisco, then place one histogram above the other.
On the screen you are seeing, we have constructed the histograms of Cisco and GM using the same bin ranges, -.3 to -.2, -.2 to -.1, and so on. By comparing these two histograms, you can draw two important conclusions:
- Typically, Cisco performed better than GM. Because the highest bar for Cisco is one bar to the right of the highest bar for GM. Also, the Cisco bars extend farther to the right than the GM bars. GM returns are up to 30% while the Cisco returns are up to 40%.
- Cisco had more variability or spread about the mean, than GM. Note that GM’s peak bar contains 59 months, whereas Cisco’s peak bar contains only 41 months. This shows that for Cisco, more of the returns are outside the bin that represents the most likely Cisco return. Cisco returns are more spread out than GM returns.
So as a stock analyst, you should go for Cisco, not General Motors.
What Are Some Common Shapes of Histograms?
In this section, we will discuss the common shapes of histograms. You can see the dataset of these types in the included Excel file. For most data sets, a histogram created from the data will be classified as one of the following:
- Symmetric
- Skewed Right (Positively Skewed)
- Skewed Left (Negatively Skewed)
- Multiple Peaks
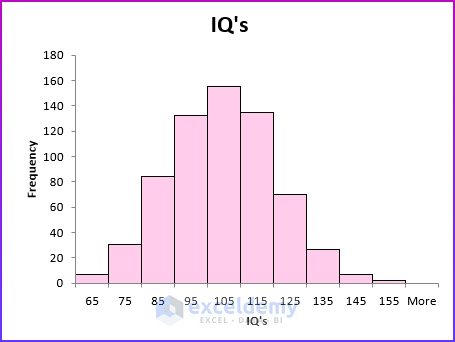
Symmetric Distribution
A histogram is symmetric if it has a single peak and looks approximately the same to the left of the peak as to the right of the peak. Test scores (such as IQ tests) are often symmetric. Notice that the height of the bars one bar away from the peak bar is approximately the same, the height of the bars two bars away from the peak bar is approximately the same, and so on.
Skewed Right – Positively Skewed
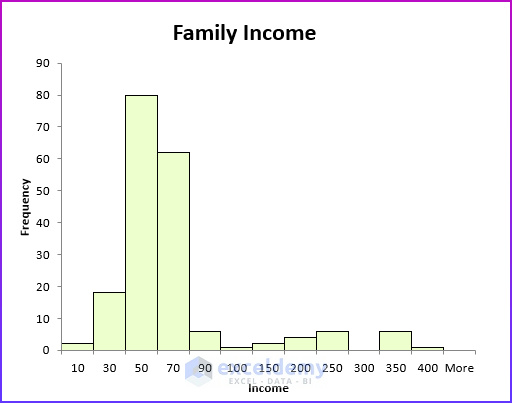
A histogram is a skewed right (positively skewed) if it has a single peak and the values of the data set extend much farther to the right of the peak than to the left of the peak. Many economic data sets (such as family or individual income) exhibit a positive skew. This figure shows an example of a positively skewed histogram created from a sample of family incomes.
Skewed Left – Negatively Skewed
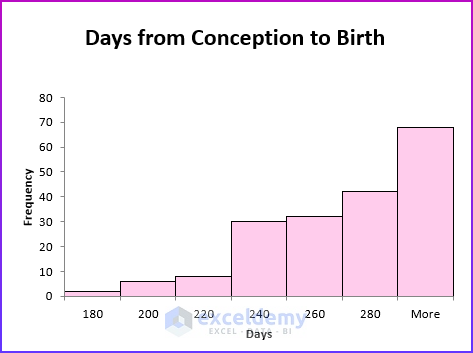
A histogram is skewed left (negatively skewed) if it has a single peak and the values of the data set extend much farther to the left of the peak than to the right of the peak. Days from conception to birth are negatively skewed. In the figure below, the height of each bar represents the number of women whose time from conception to birth fell in the given bin range.
Multiple Peaks
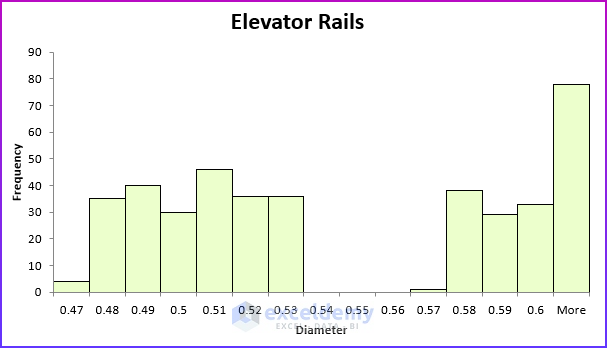
When a histogram exhibits multiple peaks, it usually means that data from two or more populations are being plotted together. For example, suppose the diameter of elevator rails produced by two machines yields the histogram shown in the following figure.
Now, let’s talk more about the twin peak or multiple peak histogram. In this histogram, the data is clustered into two groups. In all likelihood, the left group of elevator rails is produced by one machine, and the right group of elevator rails is produced by other machines.
If your required diameter for an elevator rail is “.55” inches, you can conclude that one machine is producing elevator rails that are too narrow, whereas the other machine is producing elevator rails that are too wide. And neither machine produced the required “.55” inch diameter elevator rails. This example shows why histograms are a powerful tool in quality control.
Conclusion
We have shown you quick steps to create stock return frequency distributions and histograms in Excel. If you have any questions, feel free to comment below. Moreover, this is a sample lecture of our course: Data Analysis in Excel with Statistics: Get Meanings of Data, where you will learn data analysis with 52 case studies, problems, and their solutions!
