How to Use the Solver Feature in Excel (with Practical Examples)

How to Enable Solver Feature in Excel

You can access Solver by choosing Data ➪ Analyze ➪ Solver. Sometimes this command isn’t available. You have to install the Solver add-in using the following steps:

• Choose the File
• Select Options from the menu.

• The Excel Options dialog box appears.
• Go to the Add-Ins
• At the bottom of the Excel Options dialog box, select Excel Add-Ins from the Manage drop-down list and click Go.

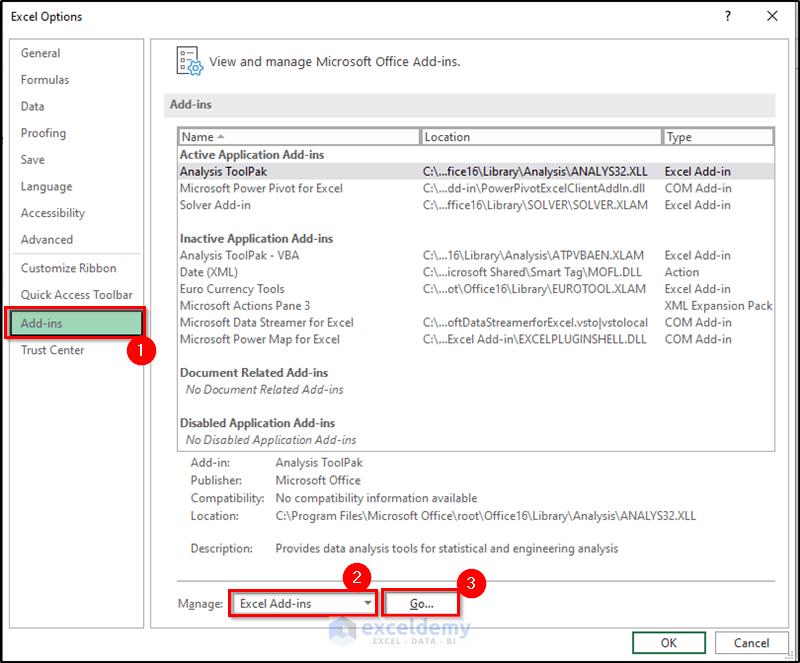
• The Add-ins dialog box appears.
• Place a checkmark next to Solver Add-In, and click OK.

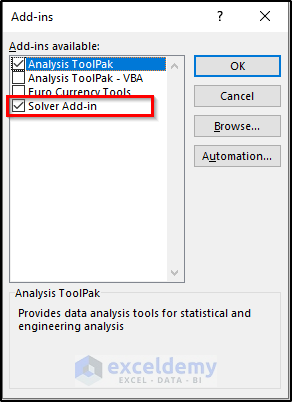
Once you activate the add-ins in your Excel workbook, they will be visible on the ribbon.

• Move to the Data tab to find the Solver add-in on the Analyze group.

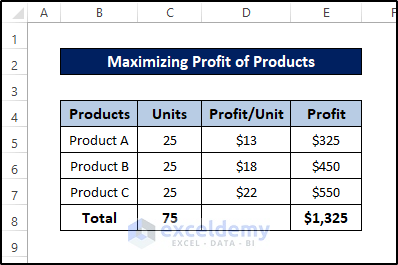
Example 1 – Using Excel Solver to Maximize Profit of Products

Below is the dataset for this example.

Steps:

• Go to the Data tab on your ribbon.
• Select Solver from the Analysis group.

• Select cell E8 as the objective cell of the Solver Parameter box.
• Next to the To: option, select Max. 
• Select the cell values we want to change in the By Changing Variable Cells (i.e., the range C5:C7).
• Add the constraints by clicking the Add button on the right of the box.
• Select Simplex LP in the Select a Solving Method box.

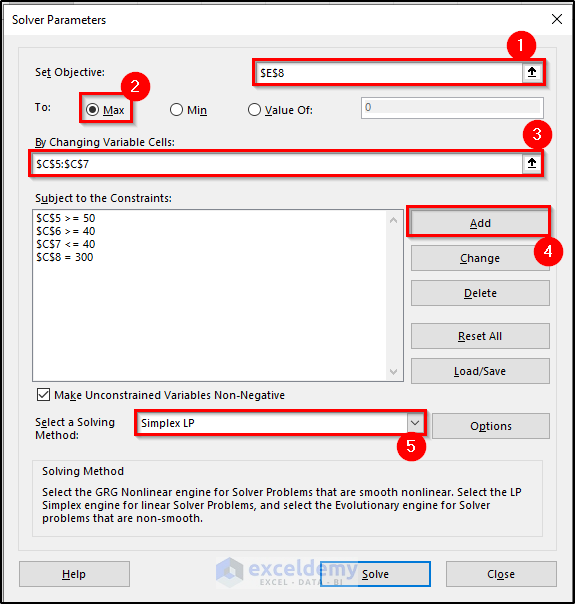
• Click Solve. The Solver Results box will appear.
• Select the options and reports you want in this box. We are enabling the Keep Solver Solution option only.

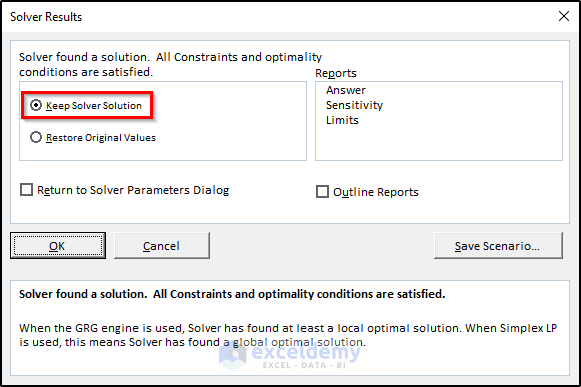
• Click OK.
• The dataset will now change to this.

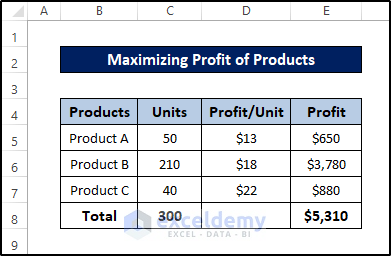
This indicates the optimum number of units required for maximum profit within the constrained entered. This is just one of the examples that demonstrate how powerful the Excel solver feature can be.

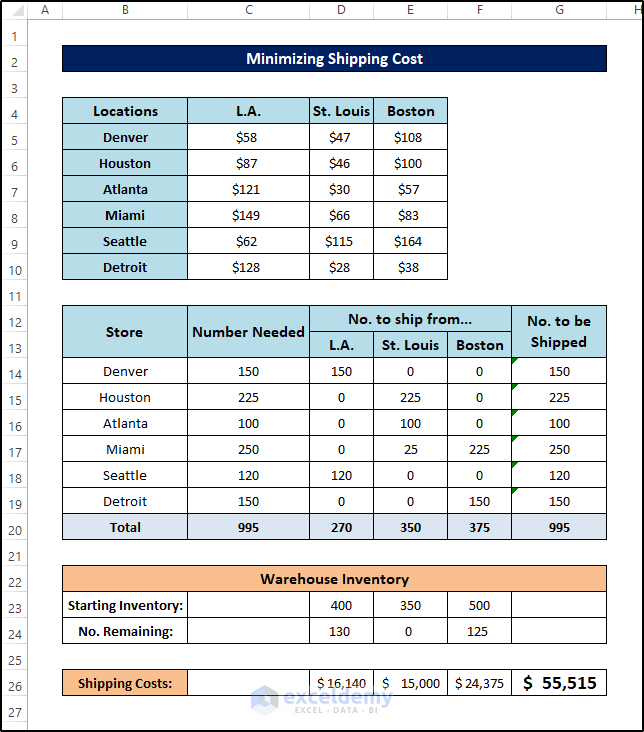
Example 2 -Using the Excel Solver for Minimizing Shipping Cost

Below is the dataset for this example.

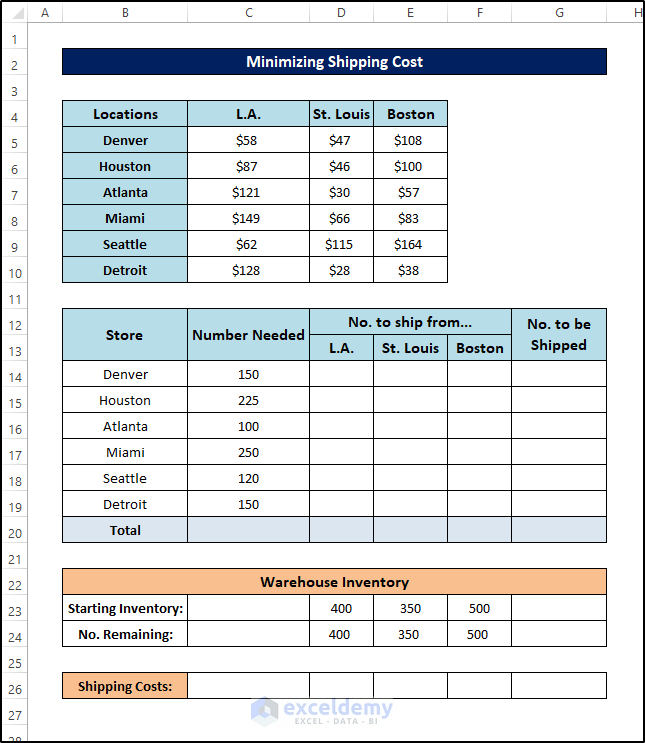
Steps:

• Enter the following formula:

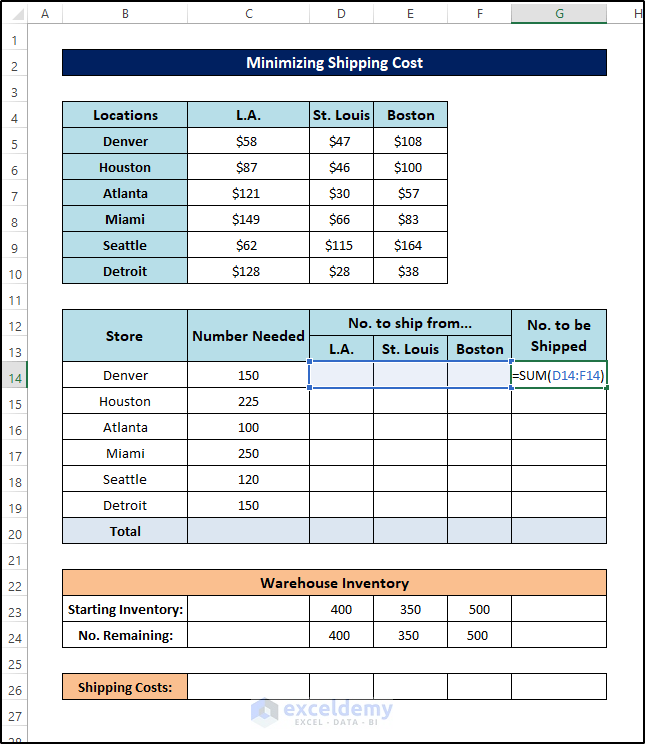
• Press Enter.

• Drag the Fill Handle icon to cell G19 to fill the other cells with the formula.
• The output will look like this.

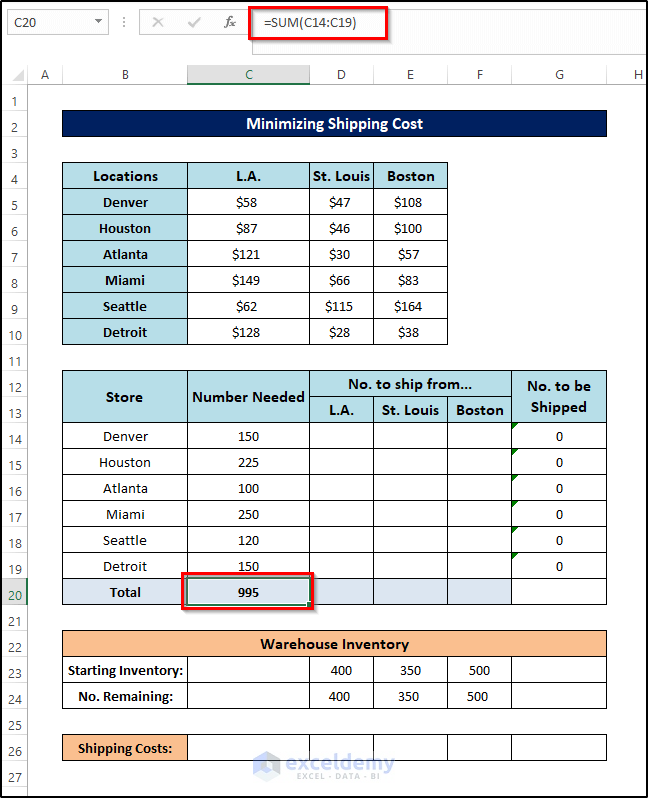
• To calculate the total, enter the following formula:

• Press Enter.

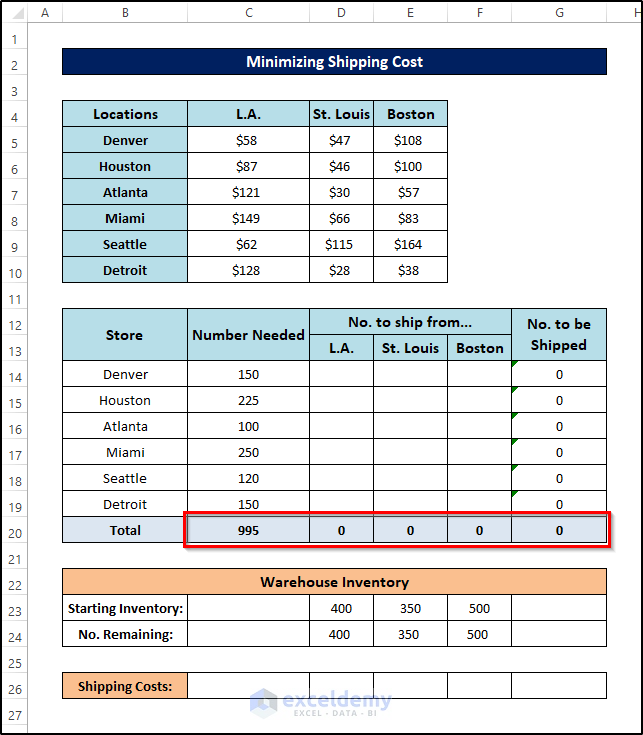
• Drag the Fill Handle icon to the right up to cell G20 to fill the other cells with the formula.

The output will look like this.

• To calculate the shipping costs, enter the following formula:

• Press Enter.

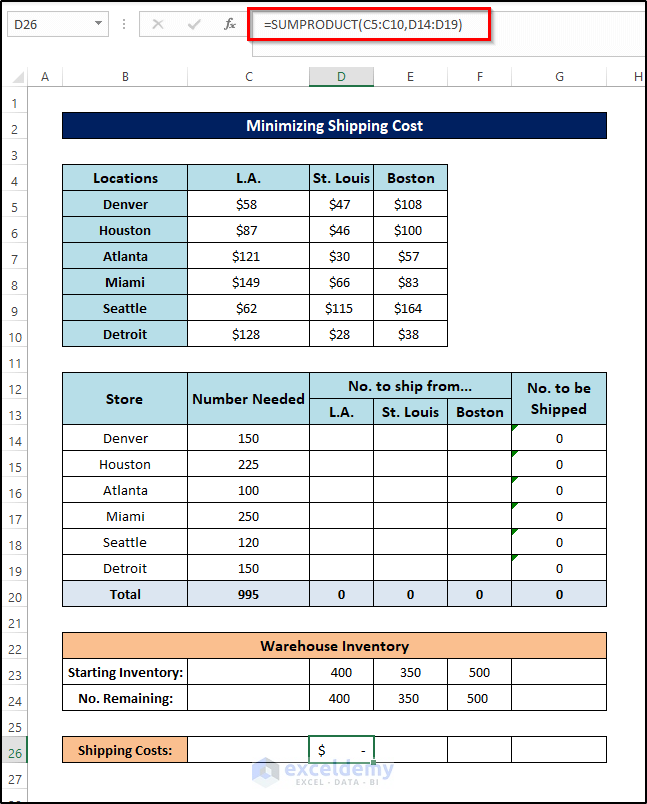
• Drag the Fill Handle icon to the right up to cell F26 to fill the other cells with the formula.
• Enter the following formula in cell G26:

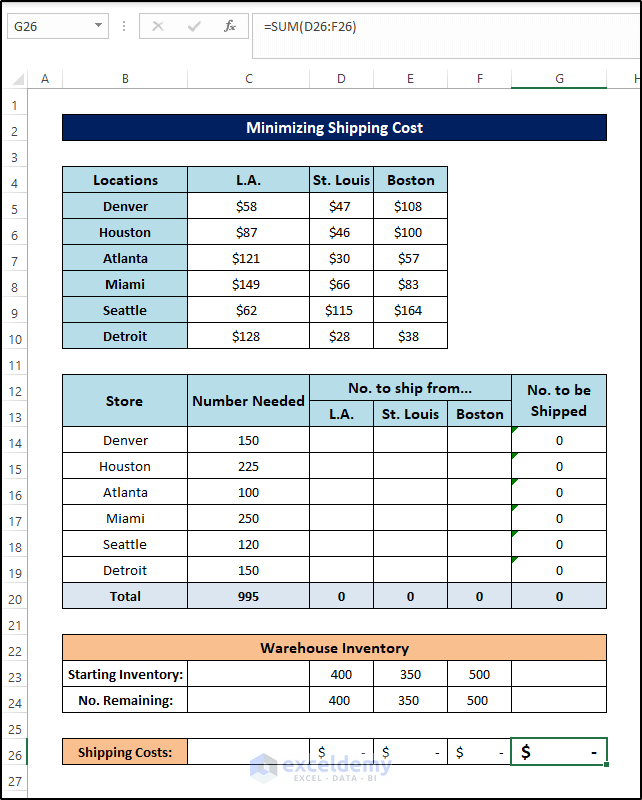
• To open the Solver Add-in, go to the Data tab and click on Solver.

• Fill the Set Objective field with this value: $G$26.
• Select the radio button of the Min option in To Control.
• Select the cell range $D$14 to $F$19 to fill the field By Changing Variable Cells. This field will then show $D$14:$F$19.
• Add constraints one by one. The constraints are: C14=G14, C16=G16, C18=G18, C15=G15, C17=G17, C19=G19, D24>=0, E24>=0, and F24>=0. These constraints will be shown in the Subject to the Constraints field.
• Select the Make Unconstrained Variables Non-Negative check box.
• Select Simplex LP from the Select a Solving Method drop-down list.

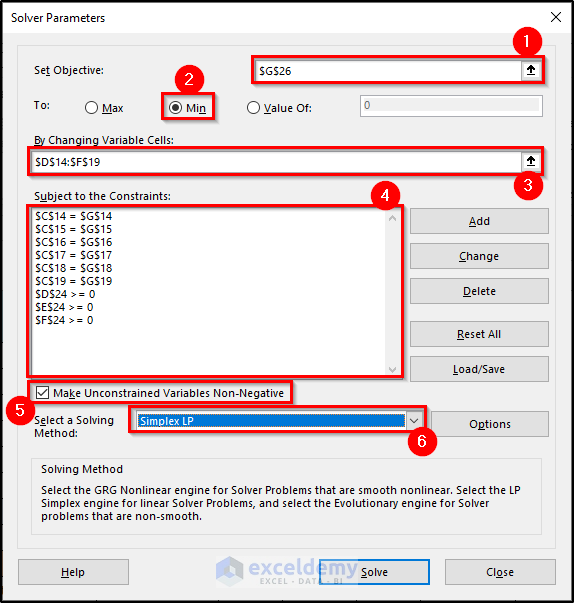
• Click Solve. The following figure shows the Solver Results dialog box.

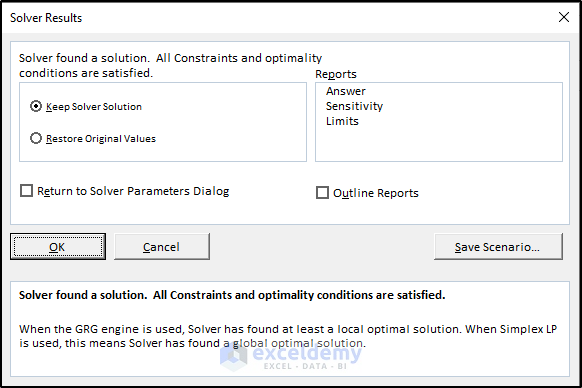
The Solver displays the solution shown in the following figure.

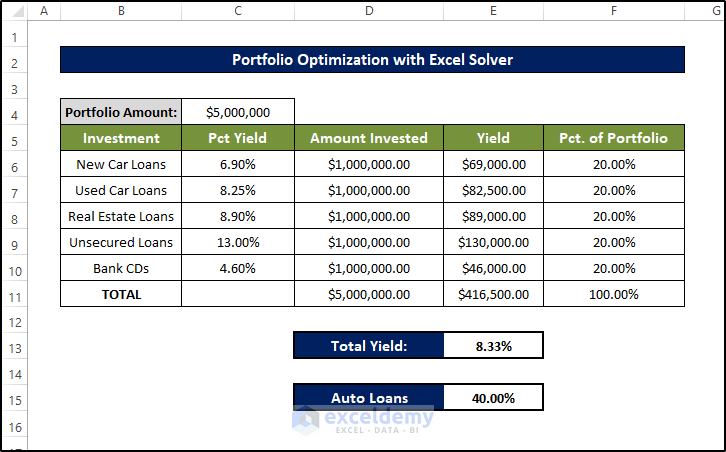
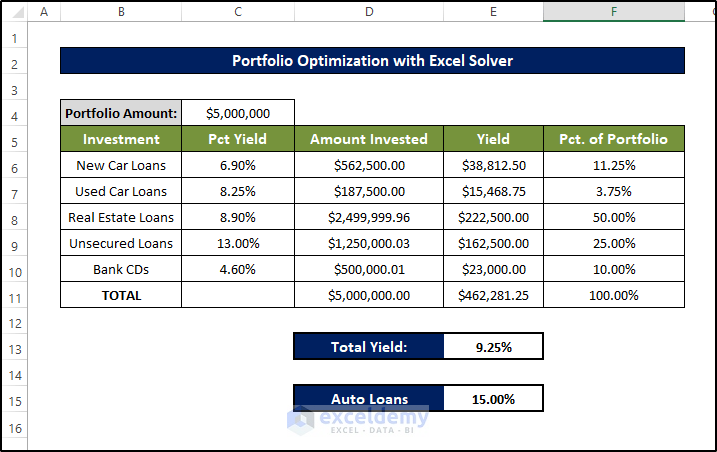
Example 3 – Using Investment Portfolio Optimization With Excel Solver

Below is the dataset for this example.

Steps:

• Select the Data
• Select Solver from the Analysis

• Fill the Set Objective field with this value: $E$13.
• Select the radio button for the Max option in To
• Select cell range $D$6 to $D$10 to fill the field By Changing Variable Cells. This field will show then $D$6:$D$10.
• Add constraints one by one. The constraints are: $D$11= $C$4 $D$6>= $D$7*3, $E$15>= 0.15, $F$9<= 0.25, $F$10>= 0.1. These constraints will be shown in the Subject to the Constraints box.
• Select the Make Unconstrained Variables Non-Negative check box.
• Select GRG Nonlinear from the Select a Solving Method drop-down list.

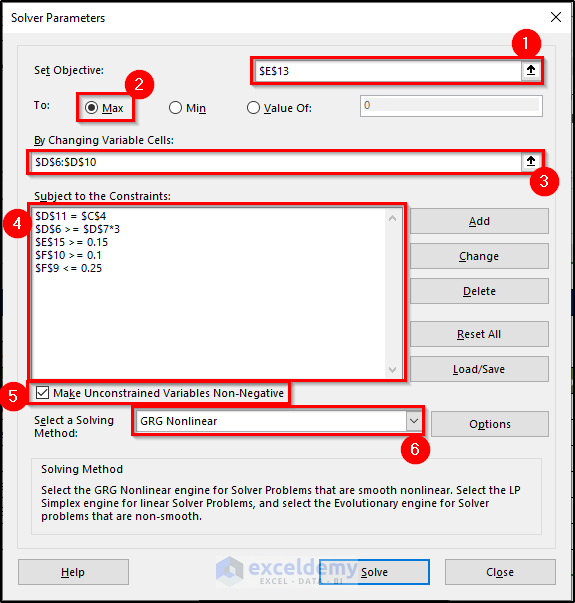
• Click the Solve Click OK.
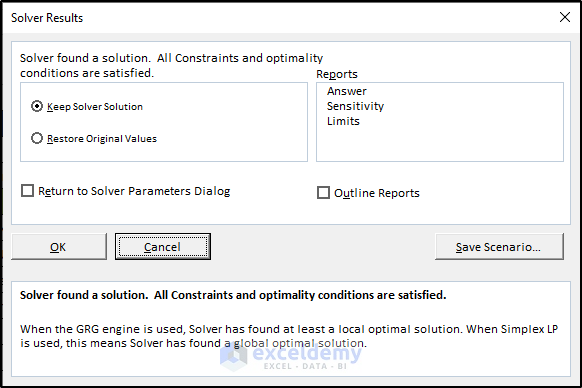
• There will be another dialog box in which you need to select the result types.
• This means you need to select Keep Solver Solution. Otherwise, the values will return to their original values.
• Then from the right side of the dialog box, select all the options in the Reports.
• Click OK.

• We’ve entered 1,000,000 in the changing cells as the starting values. When you run Solver with these parameters, it produces the solution shown in the following figure which has a total yield of 25%.
• The Auto Loans values also changed to 15%.
• This is how we got the highest optimization value for the total yield, considering all the constraints.

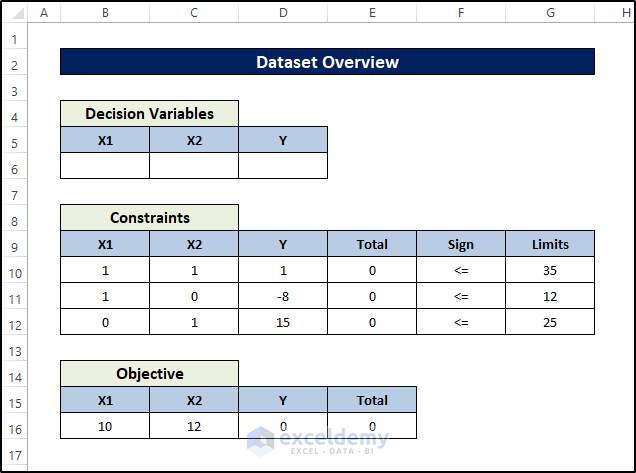
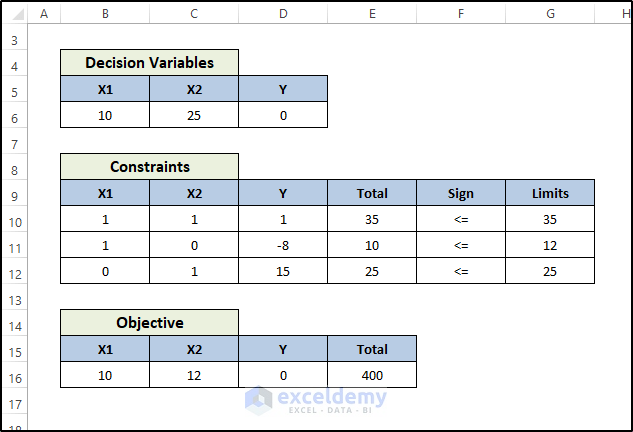
Example 4 – Using the Linear Integer Programming with Excel Solver

Below is the dataset for this example:

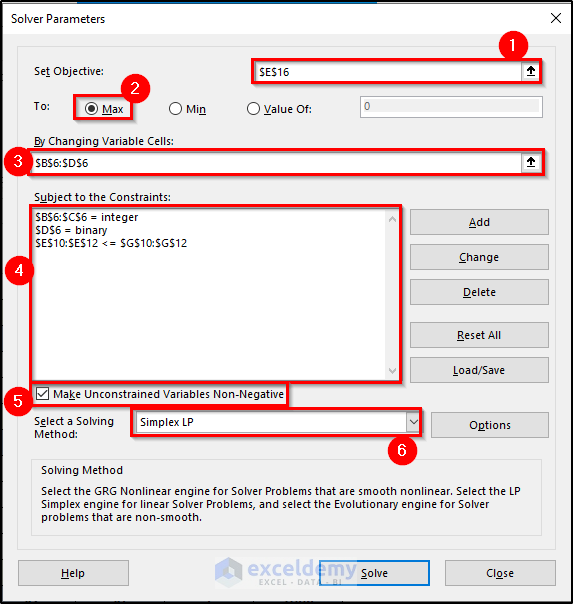
Steps:

• Go to the Data tab and select Solver from the Analysis

• Enter the values and constraints in the Solver Parameter box, as shown in the figure.

• Click Solve.
• Click OK on the Solver Results.

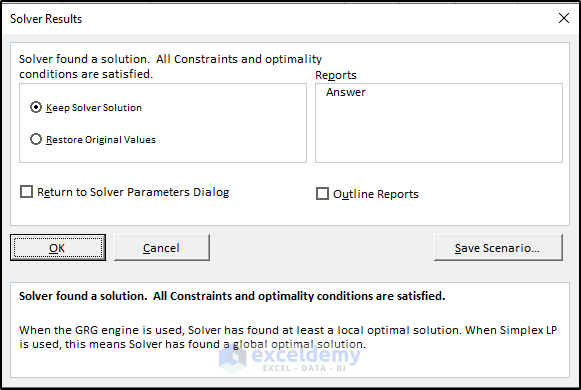
The final result of using the Excel solver on the integer linear programming example will be like this.

Read More:  Example with Excel Solver to Minimize Cost

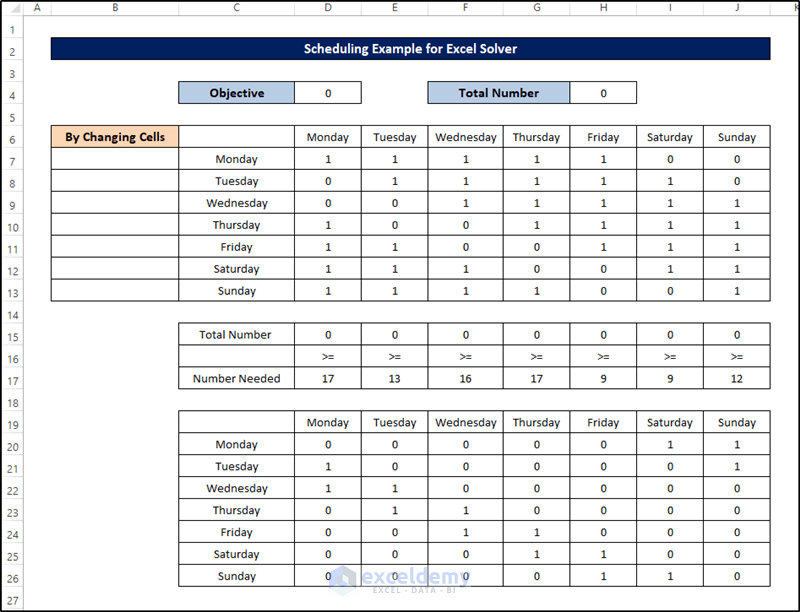
Example 5 – Scheduling with Excel Solver

Below is the dataset for this example.

Steps:

• Go to the Data tab on your ribbon and select Solver from the Analysis

• Enter the values of the constraints and the parameters, as shown in the figure below.

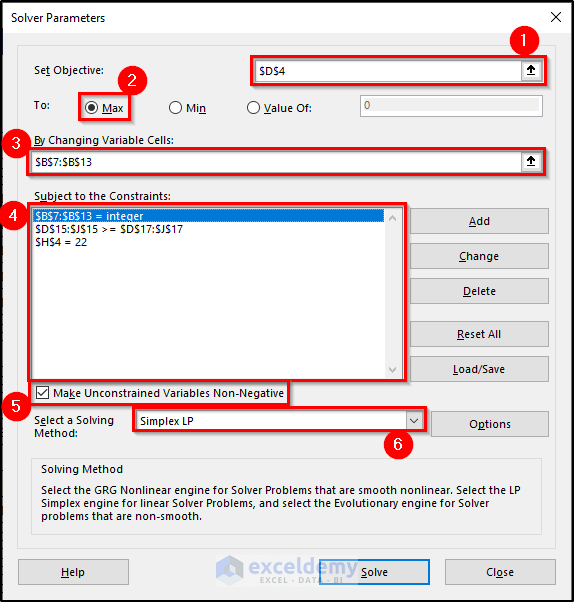
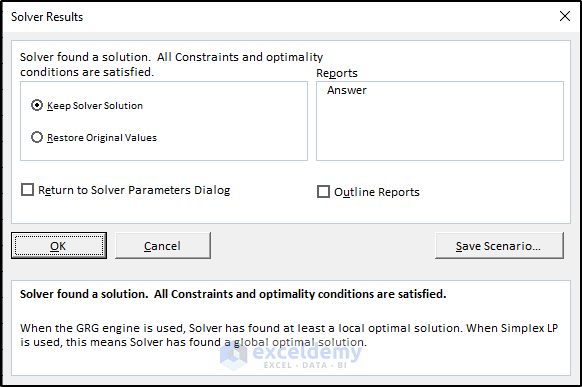
• Click Solve.
• Click OK on the Solver Results.

Because of the choices we made in the steps, the solver will automatically show the scheduling problem’s result on the Excel spreadsheet.

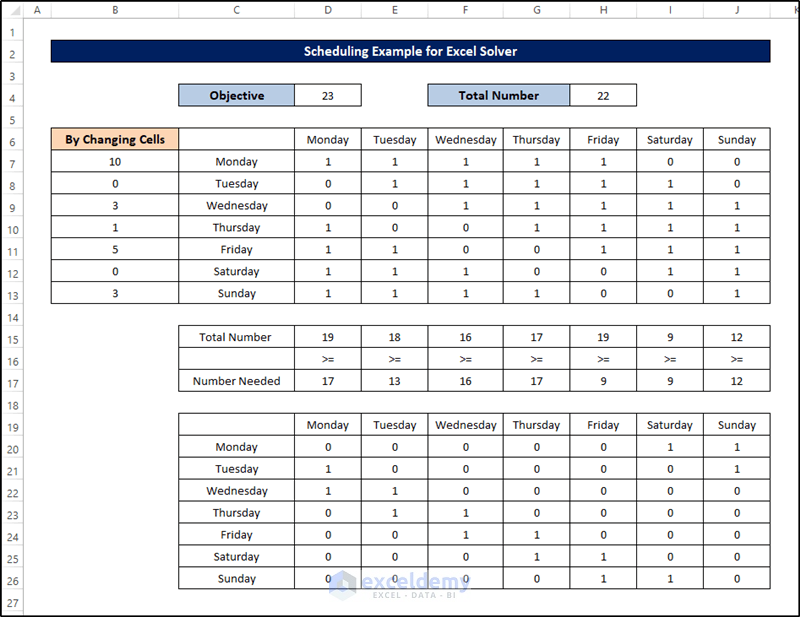
Read More: How to Assign Work Using Evolutionary Solver in Excel

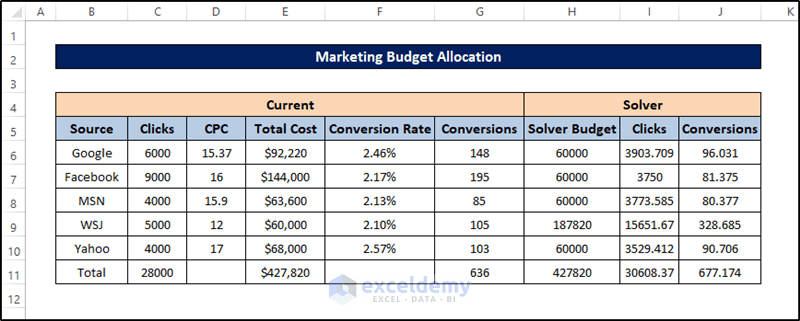
Example 6 – Using Excel Solver for Marketing Budget Allocations

Below is the dataset for this example.

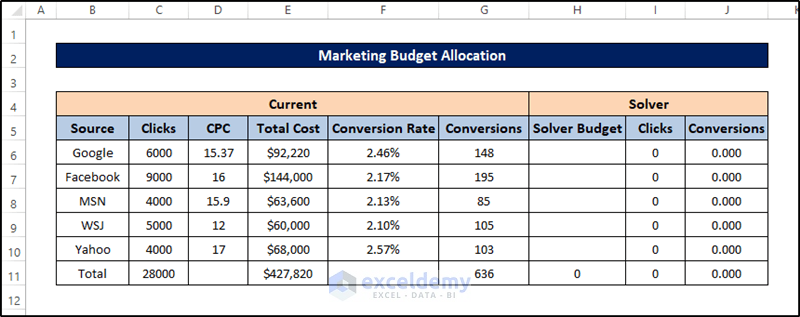
Steps:

• Go to the Data tab on your ribbon and select the Solver from the Analysis group.

• Enter the following constraints and the parameters, as shown in the figure.

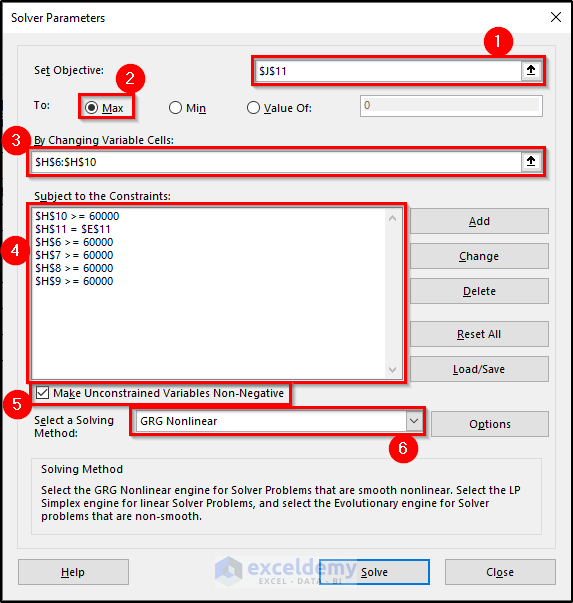
• Click Solve.
• Click OK on the Solver Results

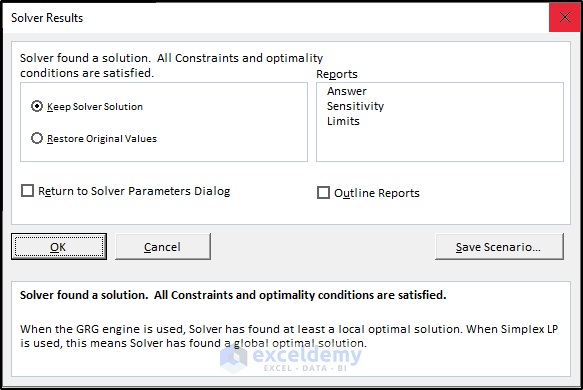
The values will change because of the constraints and parameters we have chosen.

Read More: How to Use Excel Solver for Linear Programming

Download the Practice Workbook

Download the workbook to practice.

Excel Solver Examples: Knowledge Hub

<< Go Back to Solver in Excel | Learn Excel