Aung Shine
We can use Excel to carry out many different mathematical operations. Linear Programming is an aspect of Statistics and Applied Mathematics. This has huge practical applications. Solving Linear Programming problems manually can seem a hassle. On the other hand, we have Excel Solver which can find out the solutions to those problems very readily. In this article, we’ll show you the step-by-step procedures to Use Excel Solver for Linear Programming.
Download Practice Workbook
Download the following workbook to practice by yourself.
Introduction to Linear Programming
Linear Programming is an important aspect of Statistics and Applied Mathematics. You can perform predictive analysis with prevalent data variables. It helps us in the optimization of the resources. We must have some constraints and an objective function for that purpose. The Excel Solver can quickly figure out the solutions to Linear Programming problems in Excel.
Step by Step Procedures to Use Excel Solver for Linear Programming
To illustrate, we’ll use the following business problem as an example.
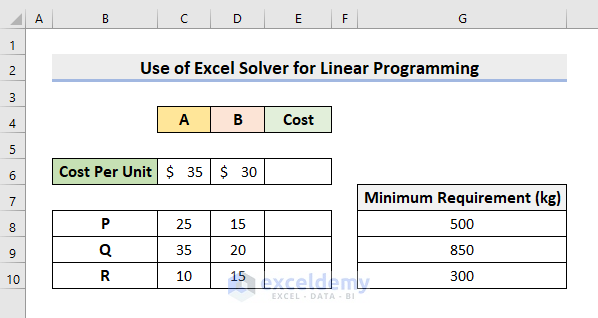
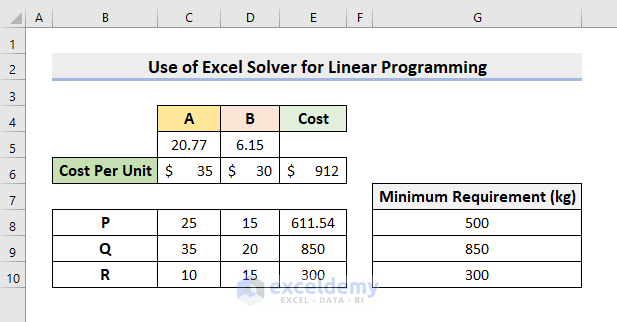
Suppose, a manufacturer has two kinds of products, ‘A’ & ‘B’. A single unit of product A requires three raw materials, P 25 kg, Q 35 kg, and R 10 kg. Similarly, B requires P 15 kg, Q 20 kg, and R 15 kg. The Manufacture needs a minimum of P 500 kg, Q 850 kg, and R 300 kg. If A costs $35 per unit and B costs $30 per unit, how many units of each product should the manufacturer blend to meet the minimum raw material requirements at a low cost as possible, and what is the price?
Now, to solve this problem, go through the below steps carefully and also learn how to use Excel Solver for Linear Programming.
STEP 1: Enable Solver in Excel
The Solver is an MS Excel add-in program. It stays deactivated by default. So, you need to enable it for using the program. Therefore, follow the process to perform the task.
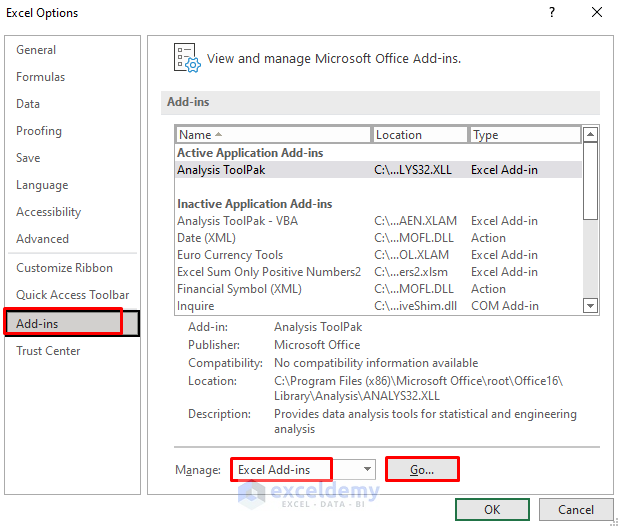
- First, go to File ➤ Options.
- Then, select the Add-ins tab.
- After that, choose Excel Add-ins from the Manage drop-down.
- Subsequently, press Go.
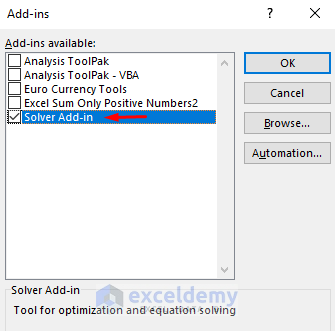
- As a result, the Add-ins dialog box will pop out.
- Now, check the box for Solver Add-in.
- Next, press OK.
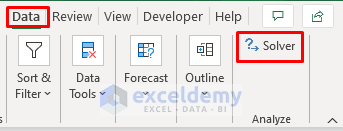
- Thus, you’ll see the Solver program in the Analyze section under the Data tab.
STEP 2: Input Constraints
In this step, we’ll input the Constraints and the Objective Function in the Excel worksheet. According to the problem, suppose, we’ll blend x units of product A and y units of B. So the total cost will be $35x + $30y. This is our objective function and we want to minimize this cost. At the same time, we have to meet the requirements. 25x + 15y >= 500, 35x + 20y >= 850, 10x+15y >= 300, x >= 0 and y >= 0 are our constraints. Now, we’ll input these.
- First of all, type the per-unit costs of A and B.
- See the following picture to understand better.
- Next, input the materials under the respective products.
- Insert the minimum required amounts.
STEP 3: Create Excel Formula
- We’ll insert the value of x in cell C5 and y in cell D5.
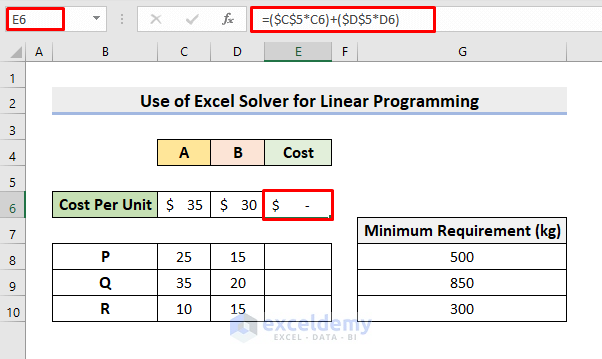
- Firstly, select cell E6.
- Then, type the formula:
=($C$5*C6)+($D$5*D6)- Press Enter.
- It’ll return 0 or blank as the C5 and D5 cell values are empty for the moment.
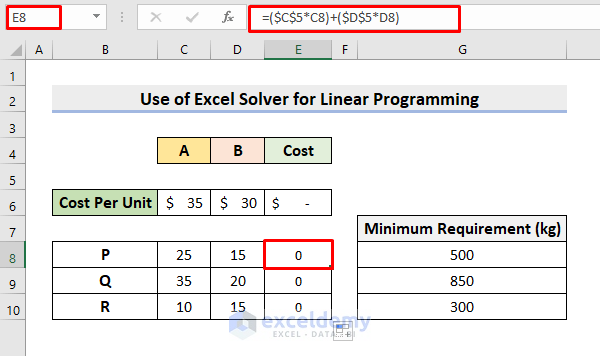
- Afterward, select the cell E8 to type the formula:
=($C$5*C8)+($D$5*D8)- Consequently, press Enter to return the values.
- Use the AutoFill tool to complete the rest.
- For now, the results are 0 as C5 and D5 are empty.
STEP 4: Solve Linear Programming with Excel Solver
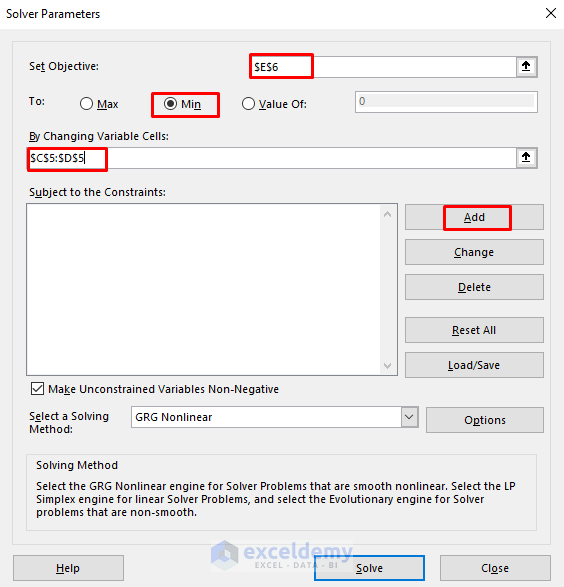
- Now, select the Solver program under the Data tab.
- Accordingly, the Solver Parameters dialog box will emerge.
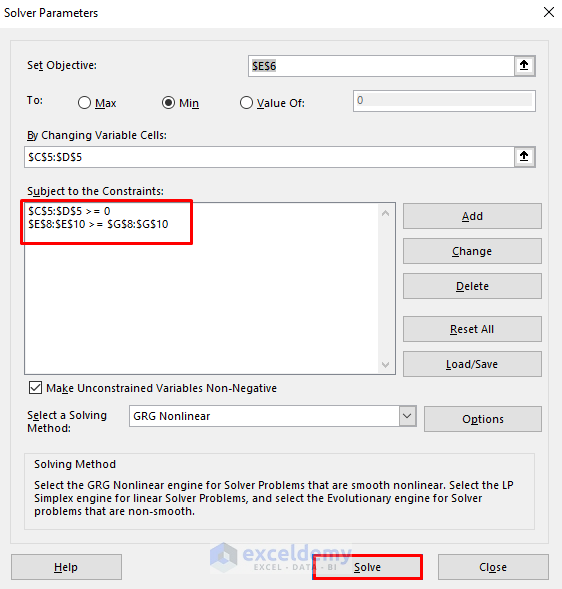
- Next, choose cell E6 in the Set Objective box.
- After that, check the circle for Min.
- Select the range C5:D5 as variable cells.
- The following image demonstrates the process clearly.
- Then, press Add for adding the constraints.
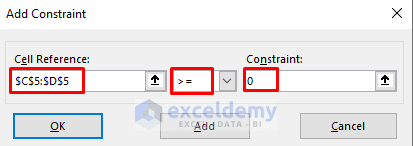
- The Add Constraint dialog box will appear.
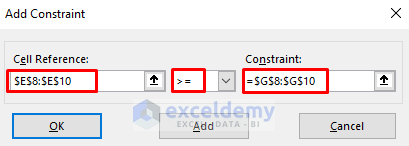
- Choose the range C5:D5 and click >= (greater than or equal to) symbol from the drop-down.
- Type 0.
- Press Add afterward.
- Moreover, choose the range E8:E10 for minimum requirement constraints.
- Click the >= symbol from the drop-down.
- Select the range G8:G10 in the Constraint field.
- Press OK.
- Hence, you’ll see the desired constraints.
- Press Solve.
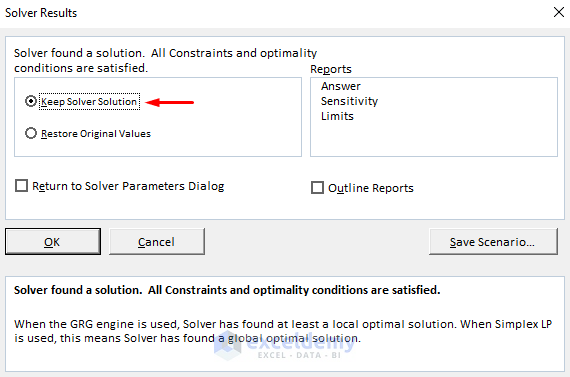
- You’ll get a dialog box about the solved results.
- Check the circle for Keep Solver Solution.
- Press OK.
- Lastly, it’ll return the precise results in the appointed cells.
Read More: How to Solve Blending Linear Programming Problem with Excel Solver
Final Output
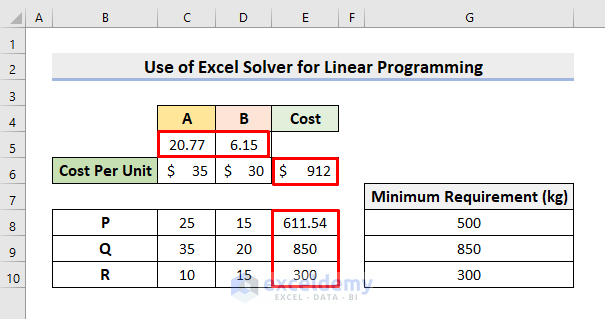
- The value of x is 77 units and y is 6.15 units.
- The minimum cost is $912.
- The optimized amounts of P, Q, and R is 54 kg, 850 kg, and 300 kg respectively.
- Therefore, the manufacturer should blend 77 units of A and 6.15 units of B.
Conclusion
Henceforth, you will be able to use Excel Solver for Linear Programming following the above-described procedures. Keep using them and let us know if you have more ways to do the task. Follow the Excel Demy website for more articles like this. Don’t forget to drop comments, suggestions, or queries if you have any in the comment section below.
