Microsoft Excel is a powerful software. We can perform numerous operations on our datasets using Excel tools and features. There are many default Excel Functions that we can use to create formulas. Many educational institutions and business companies use Excel files to store valuable data. Sometimes, we have to deal with sequencing problems in real life. Doing manually to figure out the desired sequence is a very tough job and that’s tiresome too. The Solver tool in Excel can alleviate the hassle. This article will show you 2 ideal examples of Solving Sequencing Problems Using Excel Solver Solution.
Solving Sequencing Problems Using Excel Solver Solution: 2 Suitable Examples
In every organization or institution, they maintain a work sequence taking multiple things into consideration. Aside from that, individuals also sequence their tasks to have maximum benefit and fewer costs. So, it’s essential to determine an efficient order of the jobs. Excel has an add-in tool named Solver, which specializes in performing this kind of task and outputs the best solution by solving equations in Excel. Therefore, go through the following 2 examples to carry out the operation.
1. Solving Traveling Salesman Sequencing Problem Using Excel Solver Solution
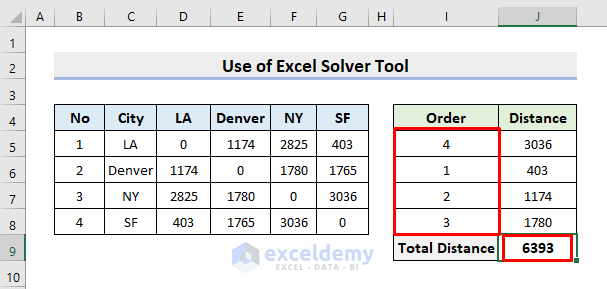
To illustrate, we’ll use a sample dataset as an example. For instance, the below dataset contains 4 Cities and the Distance between them. Here, we’ll find out a sequence of the cities for a traveling salesman so that the total distance covered will be minimal. So, follow the steps below to perform the task.
STEPS:
- First, we’ll set up a random order in the I column as shown below.
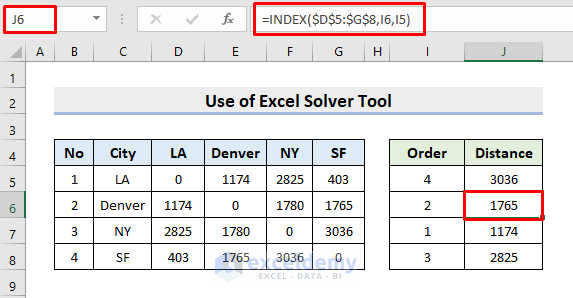
- Then, select cell J6 instead of J5.
- Type the formula:
=INDEX($D$5:$G$8,I6,I5)- Subsequently, press Enter.
- Here, the INDEX function extracts the distance between the cities specified in I6 and I5.
- Use AutoFill to get the other outputs.
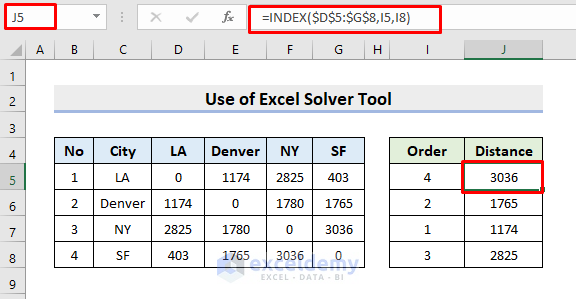
- Now, select cell J5.
- Next, input the formula:
=INDEX($D$5:$G$8,I5,I8)- Click Enter.
- Thus, it’ll give out the distance between the first and the last city.
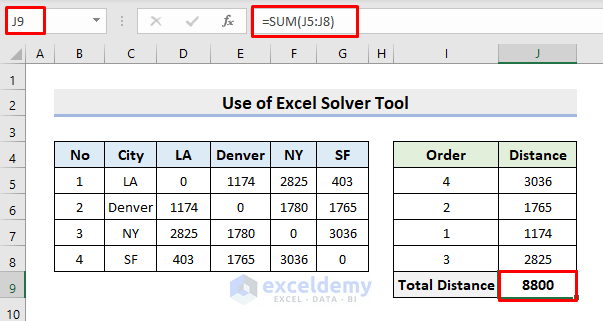
- After that, use the AutoSum feature in cell J9 to calculate the total distance.
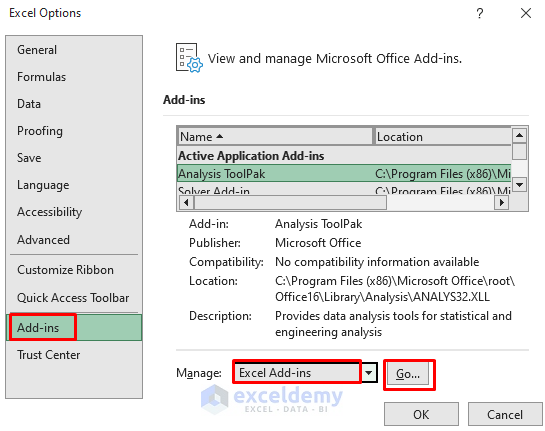
- Again, to add the Solver tool, go to File > Options.
- As a result, the Excel Options box will pop out.
- There, in the Add-ins tab, select Excel Add-ins > Go.
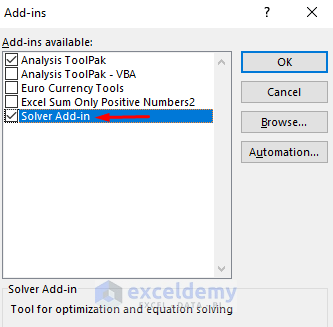
- Check the box for Solver Add-in.
- Press OK.
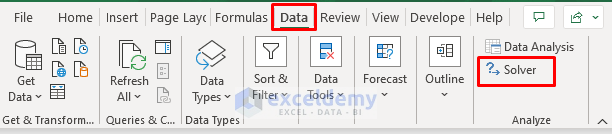
- Now, click Data > Solver.
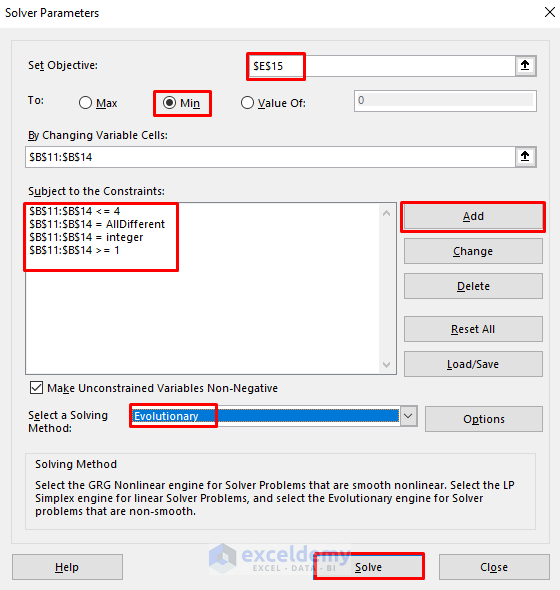
- In the Solver Parameters dialog box, select Set Objective > E15.
- Then, choose Min.
- Select B11:B14 from the data for the By Changing Variable Cells
- Next, we’ll add the constraints by clicking the Add button.
- Our constraints are:
B11:B14 <= 4
B11:B14 = AllDifferent
B11:B14 = integer
B11:B14 >= 1
- Consequently, select Evolutionary as the solving method.
- Lastly, press Solve.
- Hence, it’ll return a new sequence where the total distance is the lowest value possible.
- In this way, we can solve sequencing problems using the Solver tool.
Read More: How to Use Excel Solver for Linear Programming
2. Apply Excel Solver Solution to Solve Job Schedule Sequencing Problem
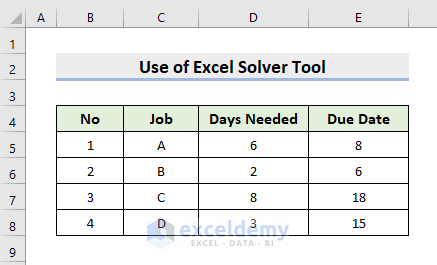
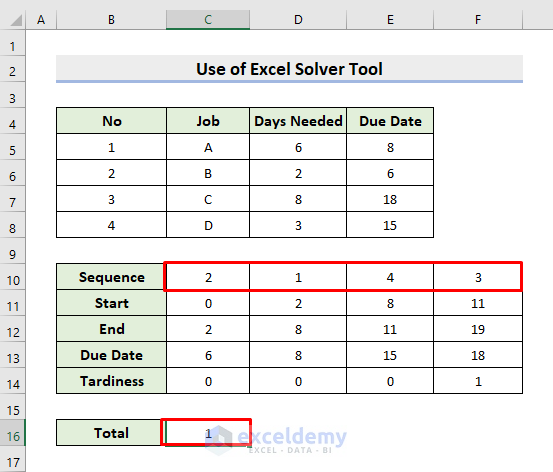
We’ll demonstrate another example of using the Solver tool to solve sequencing problems. The following dataset has 4 types of Jobs, Days Needed, and Due Dates. Here, we’ll make an order of the jobs where the Tardiness will be as little as possible. Therefore, learn the following steps.
STEPS:
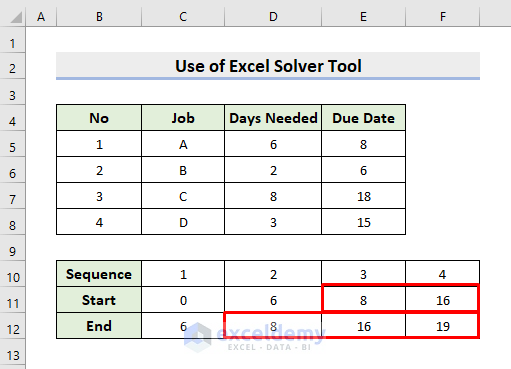
- Firstly, we’ll create a random sequence.
- Then, as a starting day, 0 is placed in cell C11.
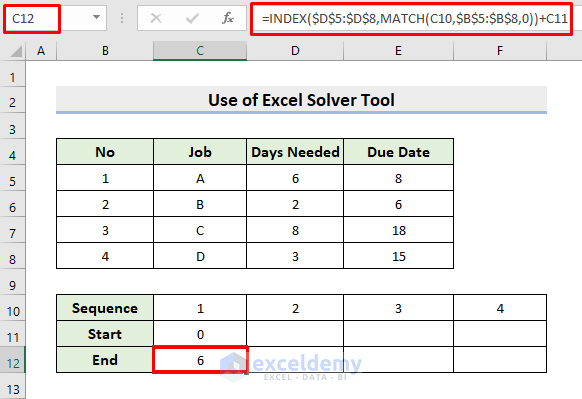
- Now, select cell C12.
- Type the formula:
=INDEX($D$5:$D$8,MATCH(C10,$B$5:$B$8,0))+C11- Next, press Enter to get the result.
- Here, the MATCH function looks for the C10 cell value in the range B5:B8 and returns the position.
- The INDEX function extracts the days needed to complete the specified task.
- Finally, the starting date is added to the function output to get the finishing date.
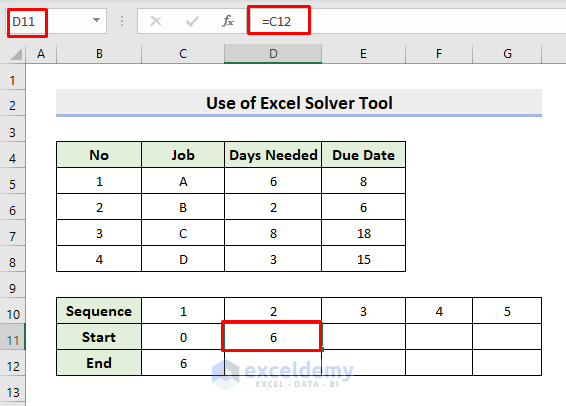
- After that, select cell D11 and input the formula:
=C12- Press Enter to get the starting date of the next task.
- Subsequently, use AutoFill to complete the starting and ending series.
- See the picture below to have a better understanding.
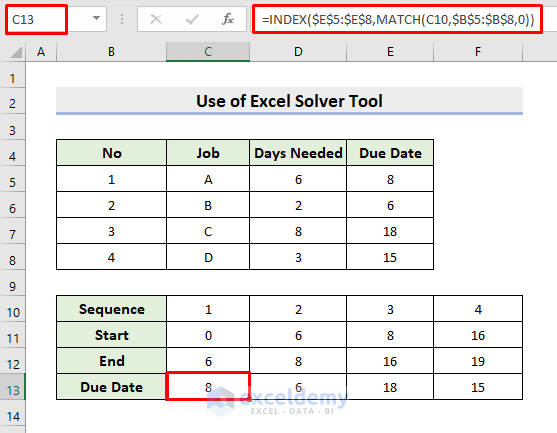
- Afterward, choose cell C13 to insert the formula:
=INDEX($E$5:$E$8,MATCH(C10,$B$5:$B$8,0))- Similarly, the MATCH function extracts the position of a specific task.
- The INDEX function returns the due date for that task.
- Apply AutoFill.
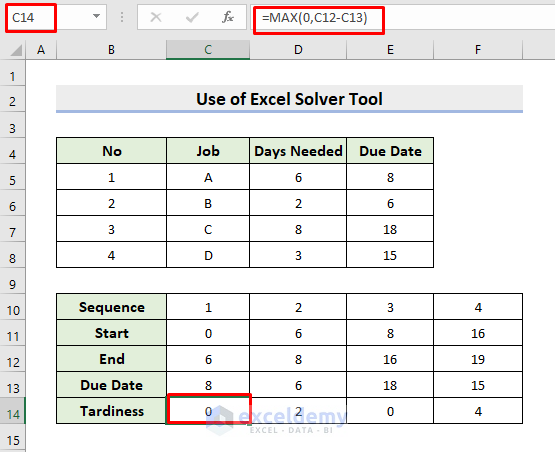
- Finally, we’ll compute the Tardiness.
- In this regard, select cell C14.
- Input the formula:
=MAX(0,C12-C13)- Click Enter.
- The MAX function compares the values and returns the largest.
- Consequently, use AutoFill.
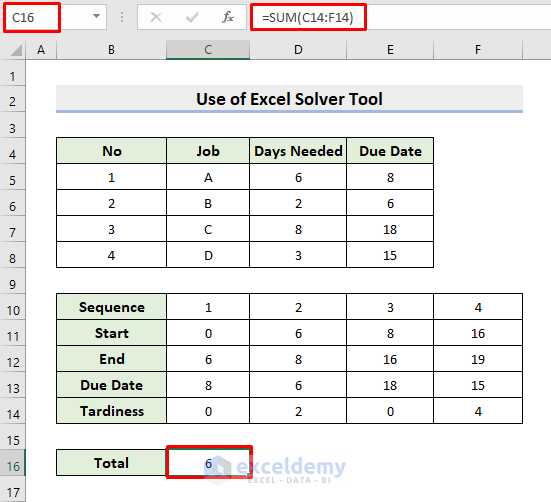
- Now, to calculate the total tardiness, click cell C16.
- Type the formula:
=SUM(C14:F14)- Press Enter.
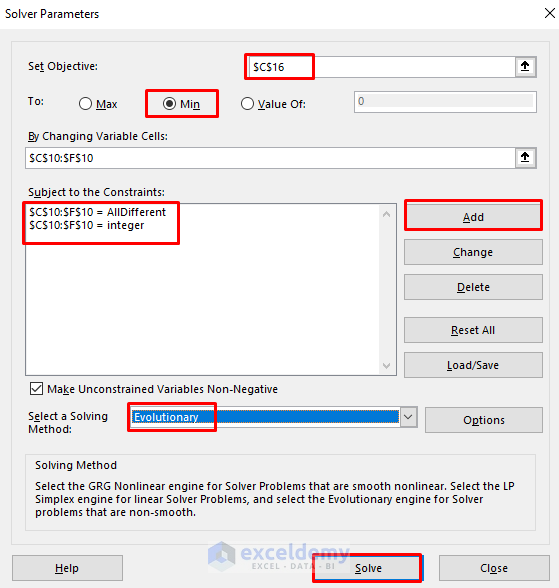
- To solve the sequencing problem, go to Data > Solver.
- In the pop-out dialog box, set C16 as the objective.
- Choose Min.
- We’ll change C10:F10 as the variables.
- The constraints in this problem are:
C10:F10 = AllDifferent
C10:F10 = integer
- Accordingly, choose Evolutionary as the solving method.
- Lastly, click Solve.
- Thus, you’ll get the best sequence with as little as possible tardiness.
- Look at the final result below.
Read More: Example with Excel Solver to Minimize Cost
Download Practice Workbook
Download the following workbook to practice by yourself.
Conclusion
Henceforth, you will be Solving Sequencing Problems Using Excel Solver Solution after learning the above-described examples. Keep using them and let us know if you have more ways to do the task. Don’t forget to drop comments, suggestions, or queries if you have any in the comment section below.
Related Articles
- How to Use Excel Solver to Rate Sports Team
- How to Use Excel Solver to Determine Which Projects Should Be Undertaken?
- Solving Transportation or Distribution Problems Using Excel Solver
- How to Assign Work Using Evolutionary Solver in Excel
- Resource Allocation in Excel
- How to Create Financial Planning Calculator in Excel
- Solving Equations in Excel
- How to Do Portfolio Optimization Using Excel Solver
<< Go Back to Excel Solver Examples | Solver in Excel | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!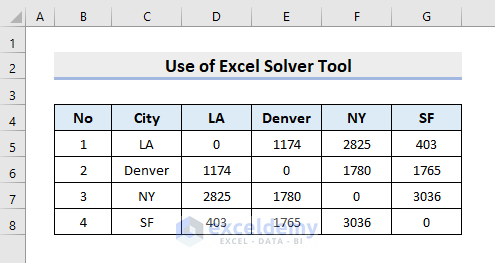



Thank you Professor for the nice and useful illustration. I teach subjects like Operations Management ad Decision Science and use Excel for solving the problems. Your methods are very helpful. Can you kindly explain how to solve sequencing problem using Johnson’s algorithm of scheduling n-jobs on 2-machines?
Greetings, Raja.
I appreciate you asking this question. You can find it here “Sequencing problem using Johnson’s algorithm of scheduling n-jobs on 2-machines”
I will pass your request to the author, Jagadeesh!
Glad to know it helped you!
Thank you for the very informative tutorial.
I would like some advice though to take the shop scheduling problem 1 step further.
How can I do this at a time/hour level – rather than day?
For example – if we have x amount of jobs in queue; varying in duration
We can only turn around jobs during standard work hours (7 AM and 4 PM).
We also need to meet delivery dates.
How do I arrange jobs in a way that maximizes machine utilization?
Greetings, LOIACONO.
I appreciate you asking this question. You have to follow the “3 Shop Scheduling Problem” example from this article. If you wish to do the calculation at a time/hour level instead of a day level, you need to input hours instead of days in the Days needed column. You must then follow the example’s rest of the process to arrange jobs in a way that maximizes machine utilization.
Nice model that can be simplified a bit because the help file for solver stats that:
“A constraint such as A1:A5 = alldifferent, where A1:A5 are decision variable cells, requires that these cells must be integers in the range 1 to N (N = 5 in this example), with each variable different from all the others at the solution.”
So constraints G3:G8=1 and G3:G8 = integer are not needed
Alf
Greetings, ALF.
It was helpful to receive the information you provided.