How to Do Portfolio Optimization Using Excel Solver (2 Easy Ways)

In this example, we’re going to demonstrate how to use Solver to get maximum return from an investment portfolio. A portfolio consists of several investments. Each investment category has its own yield. A portfolio manager can involve some constraints to reduce risk and achieve diversification goals. Without some constraints, a portfolio becomes a no-brainer. If you are curious to know how you can optimize an investment Portfolio using Excel solver, then this article may come in handy for you. In this article, we discuss how you can complete the optimization of an investment Portfolio using an Excel solver with elaborate explanations.

In our example, we have involved a hypothetical credit union. A credit union is a financial institution that takes deposits from members and invests them in loans to other members, bank CDs, and other types of investments. The credit union also distributes part of the return on these investments to the members in the form of dividends, or interest on their deposits.

This hypothetical credit union must follow some regulations regarding its investments, and the board of directors has imposed some other restrictions. These regulations and restrictions are this problem’s constraints.

How to Optimize Portfolio in Excel

The aim of portfolio optimization is to identify the optimal portfolio (asset distribution) among those that are portfolios given a certain objective. In most cases, the objective is to maximize benefits, like predicted return, while minimizing liabilities, such as financial risk.

In order to achieve this, you should build an evenly diversified portfolio for resource allocation between different types of investments. The next step is to strike the right balance between taking risks and reaping rewards with your portfolio’s assets.

An “optimal portfolio” is the goal of portfolio optimization for investors. This indicates it’s producing the maximum feasible return for the level of risk you’re willing to take. (In another, less frequent use, this term can describe a portfolio that takes the fewest possible risks in order to achieve the desired rate of return.

One way to reduce exposure to potential losses is to invest in multiple types of assets. Securities, debt, and equity are all examples of financial asset classes. The potential for return and loss associated with certain assets can also vary widely.

To put it another way, the term “systemic risk,” which characterizes how an asset class reacts to market conditions as a whole, varies significantly among asset categories. Whenever the stock market rises, for instance, commodity and bond prices typically fall. When stock prices fall, however, commodity and bond prices tend to climb.

Since commodities and bonds are high-risk asset classes, most average investors stay away from them entirely. Other options include mutual funds and exchange-traded funds (ETFs) that invest in such assets.

How to Create an Optimal Portfolio in Excel

The problem statement is described below,

The amount that the credit union will invest in new-car loans must be at least three times the amount that the credit union will invest in used-car loans. The reason is: that used car loans are riskier investments. This constraint is represented as C5>=C6*3
Car loans should make up at least 15% of the portfolio. This constraint is represented as D14>=.15
Unsecured loans should make up no more than 25% of the portfolio. This constraint is represented as E8<=.25
At least 10% of the portfolio should be in bank CDs. This constraint is represented as E9>=.10
The total amount invested is $5,000,000.
All investments should be positive or zero.

As we know all the necessary information related to the calculation, we can dive into optimizing the problem. But there is still another important to consider. We need to choose the solver method using which we are going to optimize the problem.

As our problem involves non-linear equations, we need to choose a method that can deal with the non-linearity of the problem. We, therefore, choose the GRG Nonlinear. There is another method to consider, which is known as the Simplex LP. However, this method cannot work with non-linear problems. When comparing the two nonlinear solver algorithms, GRG Nonlinear provides the most time-efficient option. So it’s better to go with the GRG Nonlinear for this problem.

The Downside of GRG Nonlinear

The problem with this approach is that its output is highly sensitive to the initial variables and could not be the best possible answer everywhere. A solution that is not necessarily optimal globally may be found in the solver stops at the locally optimal value close to the initial conditions.
Also, the function needs to be smooth for the GRG nonlinear algorithm to be able to find a decent solution. The IF, VLOOKUP, and ABS functions, among others, introduce discontinuities that will disrupt the operation of this algorithm.

The following figure shows a workbook set up for this problem. The problem has an investment in various sectors, with all the necessary formulas. Based on this problem, we will try to maximize or minimize the Total Yield or Auto Loans values.

1. Optimizing Investment Portfolio Based on Total Yield Using Excel Solver

The credit union is going to invest $5 million in various sectors. How this amount will be allocated is subject to the following constraints.

Steps

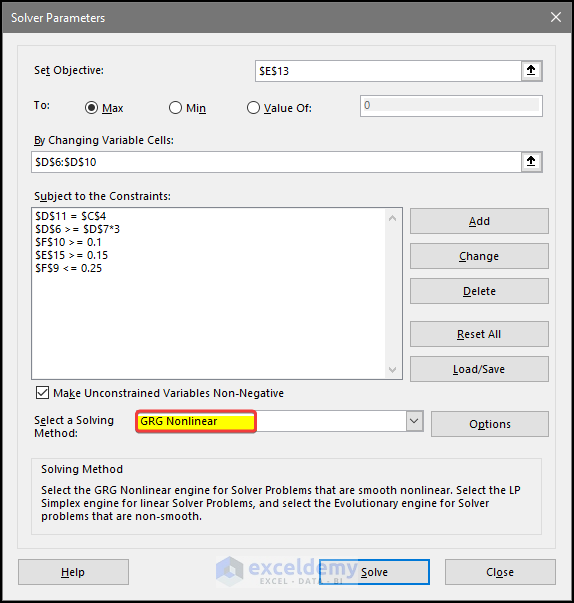
Use the following steps to set up the Solver Parameters dialog box. This dialog box appears when you choose Data ➪ Analysis ➪ Solver.

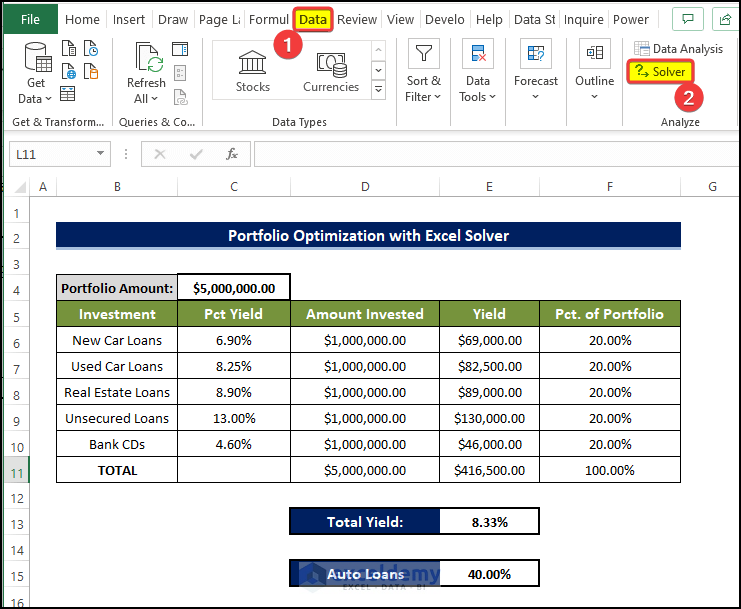
Fill the Set Objective field with this value: $E$13.
Select the radio button for the Max option in To Control.

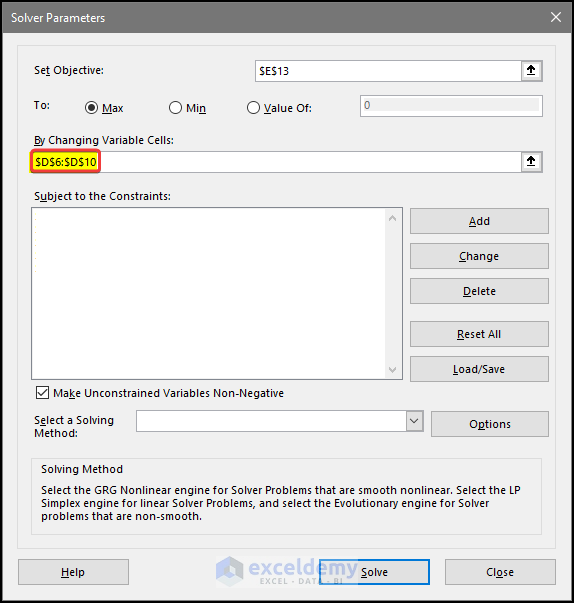
Select cell $D$6 to $D$10 to fill the field By Changing Variable Cells. This field will show then $D$6:$D$10.

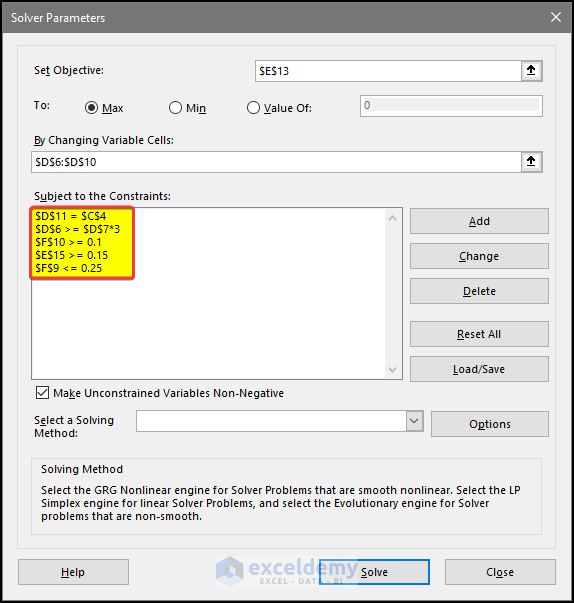
Add constraints one by one. The constraints are: $D$11= $C$4 $D$6 >= $D$7*3, $E$15>= 0.15, $F$9 <= 0.25, $F$10>= 0.1. These constraints will be shown in the Subject to the Constraints field. Click this article to learn more about adding constraints.
Select the Make Unconstrained Variables Non-Negative check box.

Select GRG Nonlinear from the Select a Solving Method drop-down list.

Now click the Solve button. Click OK.
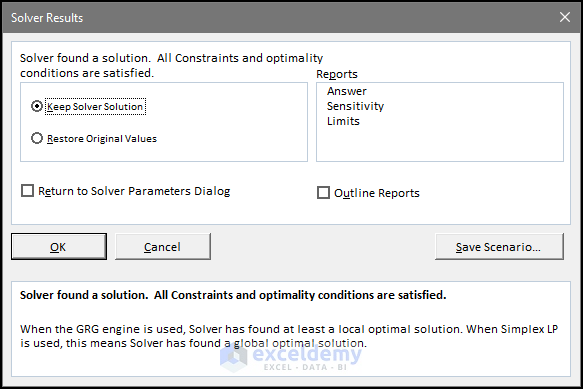
There will be another dialog box in which you need to select the result types.
Meaning, you need to select Keep Solver Solution. Otherwise, the values will revert to the original values.
Then, from the right side of the dialog box, select all the options in the Reports.
Then click OK after this.

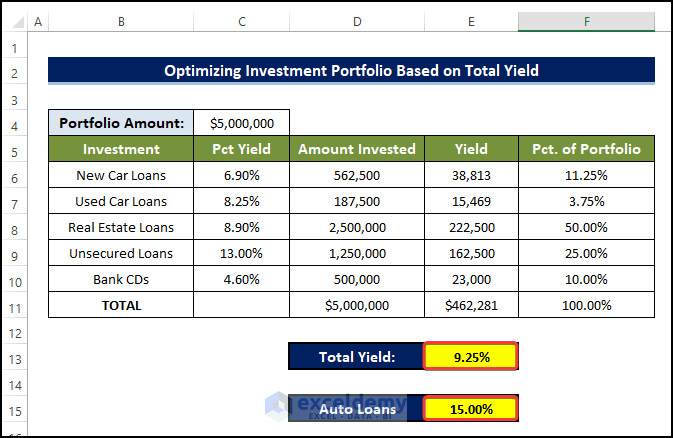
We’ve entered 1,000,000 in the changing cells as the starting values. When you run Solver with these parameters, it produces the solution shown in the following figure which has a total yield of 9.25%.
The Auto Loans values also changed to 15%.
And this is how we got the highest optimization value of Total Yield considering all the constraints.

And this is how we complete the optimization of an investment portfolio using the Excel solver.

2. Optimizing Investment Portfolio Based on Auto Loans with Excel Solver

Now we have solved a problem related to optimizing the Investment amount while trying to maximize the Total Yield value. In the next example, we will try to minimize the Auto Loan in contrast to the Total Yield in the previous example.

Steps

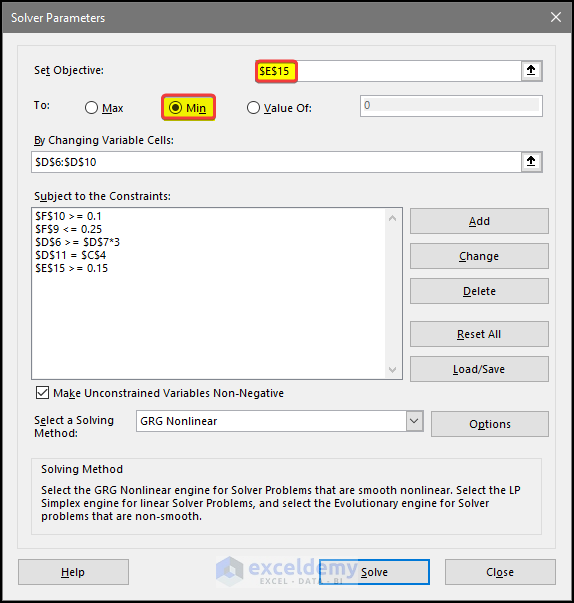
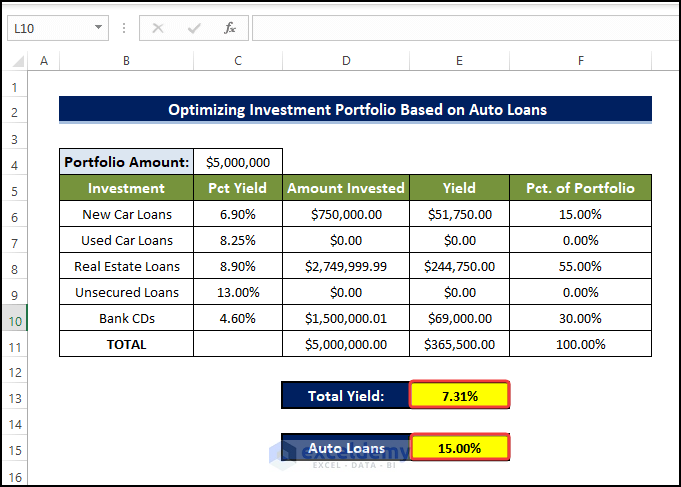
Our main goal would be to try to minimize the Auto Loans.
For this, we will select cell E15. The location of the Auto Loan value as the Objective value.
Next, we will set Min in the To option.
Doing this will make sure that the solution will try to minimize the Auto Loan value while finding a solution.
Keep all the constraints the same as before.
Click OK after this.
Clicking OK will run the Solver.

After clicking Solver, the solver will Run.
After the Solver had finished the calculation, we can see that the minimized Loan value based on all the other criteria is present.
And it also affected the Total Yield value in E13.

Download Practice Workbook

Download this practice workbook below.

Optimize Investment Portfolio.xlsx

Conclusion

To sum it up, the issue of how we can complete the optimization of an investment Portfolio using an Excel solver is answered here by 2 different examples.

For this problem, a macro-enabled workbook is available to download where you can practice these methods.

Feel free to ask any questions or feedback through the comment section.

<< Go Back to Excel Solver Examples | Solver in Excel | Learn Excel

Get FREE Advanced Excel Exercises with Solutions!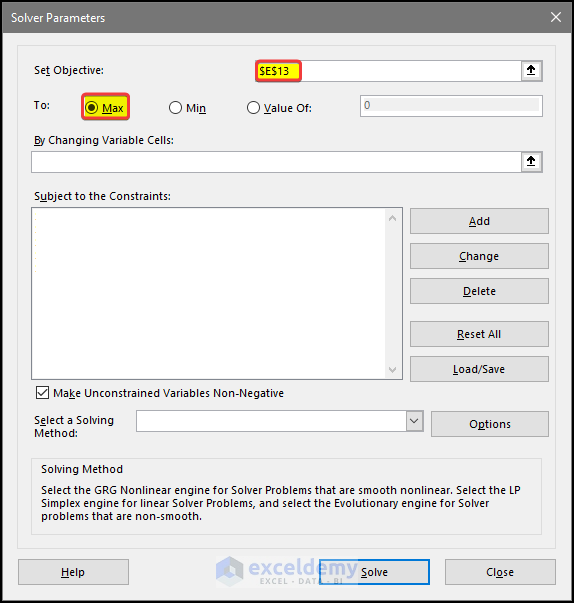

3 Comments

Harrison Delfino May 2, 2017 at 8:47 AM

I am using MarketXLS. It works great for me.
Evangeline Sep 2, 2023 at 11:52 AM

Hi , Great Work !!! Thank you for this informative post ! Do you get these questions from a book or do you write them yourself ? If you use a book would you mind sharing its name if not again wonderful post . All the best.
- Reply
  Shamima Sultana Sep 3, 2023 at 12:16 PM
  
  Dear Evangeline,
  
  Thanks for your appreciation. Our experienced writers write these questions after doing a complete research about the topic.
  
  Regards
  ExcelDemy