Almost two weeks ago, Jagadeesh asked me if I can explain how to solve the sequencing problem using Johnson’s algorithm of scheduling n-jobs on 2-machines. I tried several approaches and found that Excel Solver is still the best approach. However, we may need to change the job sequence returned by Excel solver slightly when there are several possible sequences that can lead to an optimized result.
What is Johnson’s algorithm?
Objective
As for the task of scheduling jobs in two work centers, the primary objective of Johnson’s algorithm is to find an optimal sequence of jobs to reduce both makespan and the amount of idle time between two work centers.
Precondition
This kind of problem has the following preconditions: 1) the time for each job must be constant; 2) Job sequence does not have an impact on job times; 3) all jobs must go through first work center before going through the second work center; 4) There must be no job priorities.
Read More: Deal with Sequencing Problems Using Excel Solver!
Problem
Now I’d like to take an example to explain how Johnson’s algorithm works. Suppose that Andrew and Julie work together to write reports for projects every month. They forgot to check their calendar this month and it turned out that they need to finish as soon as possible. Assume that Andrew writes and edits reports while Julie collates data and draws all the necessary graphs. Julie starts her work on a report as soon as Andrew finishes his part. And Andrew works continuously. Times for the reports (in hours) are as follows. What is the order of the tasks using Johnson’s rule?
| Projects | Andrew | Julie |
| A | 4 | 2 |
| B | 3 | 5 |
| C | 5 | 1 |
| D | 7 | 3 |
| E | 8 | 6 |
Solve using Johnson’s rule
First of all, we need to list the jobs and their times at each work center. Since above table already gives us the required information. I will move forward to the next step.
The smallest time in Work Center B (Julie in our problem) is located in Job C (1 hour). The smallest time in work center A (Andrew in our case) is located in Job B (3 hours) after eliminating Job C. Therefore, job B will be scheduled first and Job C will be scheduled last.

Figure 1.1
Find the next two smallest times after eliminating Job B and C, we will get the below sequence. Please note that this process should be repeated until only one job or no job is left.

Figure 1.2
The only job left to be considered is Job D and the final job sequence is as below.

Figure 1.3
Logic to get target cell for above problem
There are three elements essential for the Excel solver: target cell, by changing cell and constraints. If you have already read this article (Deal with sequencing problems using Excel Solver), you will know that job sequence is our by changing cell and above preconditions can be our constraints. The only left thing is how to get total time or makespan?
The left panel in Figure 2.1 shows you the job sequences of the above problem and their corresponding times. The right panel illustrates the total time. One square represents one hour. For example, Andrew needs 3 hours to finish Job B and I put 3 yellow squares at the beginning of the second row. Since Julie needs 5 hours to finish Job B and she can only start after Andrew finishes Job B, 5 yellow squares were placed after 3 white squares for the third row. White squares represent idle time.
Andrew can only be idle when he finishes all those five jobs and when he is idle, Julie is working. Therefore, the sum of total hours that Julie spends on working and total hours that Julie is idle determines the total time (makespan). We already know the total time that Julie will spend on work per the problem. The question here is that how to calculate Julie’s idle time?
Read More: Use Excel Solver to Determine Which Projects should be Undertaken
First kind of situation
Look at Figure 2.1. When Andrew works on his first job, Julie will be idle. Thus, the time of the first Job for Andrew should be taken into consideration when computing Julie’s idle time. In the 9th hour, Julie is idle again and that state lasts for 3 hours. Since she already finishes her first job and has to wait for Andrew to finish the second job. Well, it seems that time of the second job for Andrew minus the time of the first job for Julie will be the idle time for Julie after she finishes her first job. Similarly, we can use the same logic to get the length of other idle time for Julie.
Second kind of situation
So far, it looks like that we already get the logic and we can set up our model now. But wait, please. What if Andrew starts the nth job while Julie is still working on her (n-1)th job? Figure 2.2 gives you another job sequence.
Look at the job A and job C. 5 hours (that Andrew needs to finish Job C) minus 2 hours (that Julie needs to finish Job A) equals to 3 hours. Per our previous logic, Julie should be idle for 3 hours after she finishes Job A. But if you look at Figure 2.2, you will find that Julie has been idle for only 1 hour. What happened? It’s because that when Andrew starts on job C, Julie is still working on Job E. 4 hours (that Andrew needs to finish Job A) minus 6 hours (that Julie needs to finish Job E) equals to -2 hours. We need to add -2 and 3 together to get the right idle time.
Third kind of situation
Let’s move on and see the last kind of situation. 7 hours (that Andrew needs to finish the 5th job) minus 1 hour (that Julie needs to finish the 1st job) equals to 6 hours. 5 hours (that Andrew needs to finish the 4th job) minus 2 hours (that Julie needs to finish the 3rd job) is 3 hours. We don’t need to add 3 into 6 since 3 is greater than 0 per the first kind of situation. Therefore, the idle time will be 6 hours. But Figure 2.3 tells that Julie should finish Job C 5 hours earlier than Andrew finishes Job D. What’s wrong?
Look at Figure 2.3 again, Julie finishes job A (third job) 1 hour later than Andrew finishes job C (fourth job). It means that Julie’s idle time is -1 hour after she finishes job A. if we add 6 and -1 together, we will get 5 hours. Well, what we need to add is minus idle time.
Let’s start from the beginning. The sum of (-3) and (-1) equals to -4. This is inconsistent with Figure 2.3. Indeed, Julie finishes the second Job 4 hours later than Andrew finishes the third Job. And -4 + 3 equals to -1. This is inconsistent with what we discussed in the previous paragraph.
In summary, there is a chain. We need to start from beginning and compute idle time one after one. When computing, if the previous idle time is less than 0, we need to add previous idle time and results from deduction together.
One more thing that I have to remind you is that minus idle time is only used to compute idle time for the next job. When computing target cell, we need to consider them as 0 since there is no white square. Is that right?
Summary
In summary, here is how to get idle time for work center B (Julie for this problem):
- Time of the first job in work center A (Andrew in our case) is a default idle time
- Calculate Time of nth job in work center A – Time of (n-1)th job in work center B for n >= 2
- Add result from step 2 together with idle time if idle time in work center B after (n-1)th job finishes is less than 0. Otherwise, the result from step 2 will idle time.
- Repeat step 2 and step 3 until we reach the last job in the sequence
- If idle time computed per above logic is less than 0, the idle time will be considered as 0. Otherwise, leave it as it is.
- Add the default idle time and idle time got from step 5 to calculate the total idle time.
Case 1: Get order of the tasks for students who work together to write reports
Problem
The problem here is the same as the above problem which is about writing reports.
Set up model
First of all, we need to list jobs and times in range B2:D7. And in range A3:A7, I will each job a number. These numbers will be values of our by changing cells. Our changing cells are range C10:C14. Formulas “=VLOOKUP ($B10, $A$2: $D$7, 3, FALSE)” were copied from cell C10 into range C11:C14 to get the time of each job for Andrew. Formulas “=VLOOKUP ($B10, $A$2: $D$7, 4, FALSE)” was copied from D10 into range D11:D14 to get the time that Julie needs to finish each job. The formula “=VLOOKUP ($B10, $A$2: $D$7, 2, FALSE)” was copied from A10 into A11:A14 to return the Job name per job number in column B.
The default idle time is C10. Formulas to compute idle time were listed in range G11:G14. The formula in range I10:I14 can return 0 if the idle time is less than 0. The formula “=SUM (D10: D14) + SUM (H10: H14)” in cell D16 is used to get our objective – makespan.
Per Johnson’s rule, C10 and D14 should contain the smallest time for Andrew and Julie respectively. Therefore, SMALL function was used here to retrieve those two smallest times.
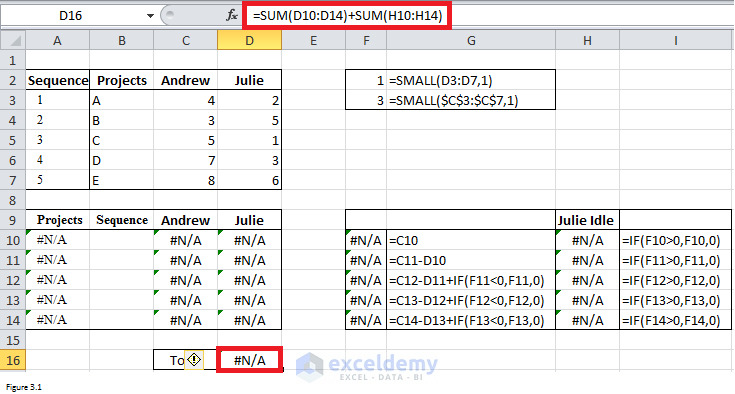
Figure 3.1
Fill Solver Parameter dialog box as shown in Figure 3.2. If you don’t know how to open this dialog box, please read this article. The values in by changing cells should be different from each other. At the same time, they should be integers between 1 and 5. The other two constraints are about two smallest times per Johnson’s rule.
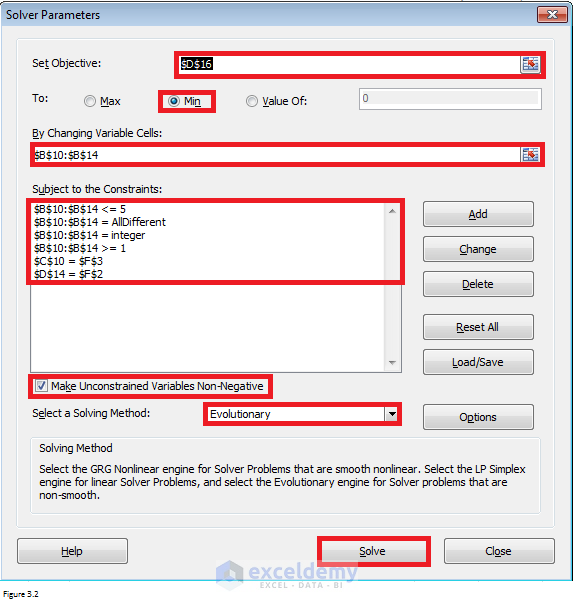
Figure 3.2
Results
After clicking on Solve in Solver Parameter dialog box, Excel will return results as shown in Figure 3.3. If they work to follow the sequence of B ‑> E ‑> D ‑> A ‑> C, they can finish reports using the least time – 28 hours. And there are total 11 hours that Julie will be idle.
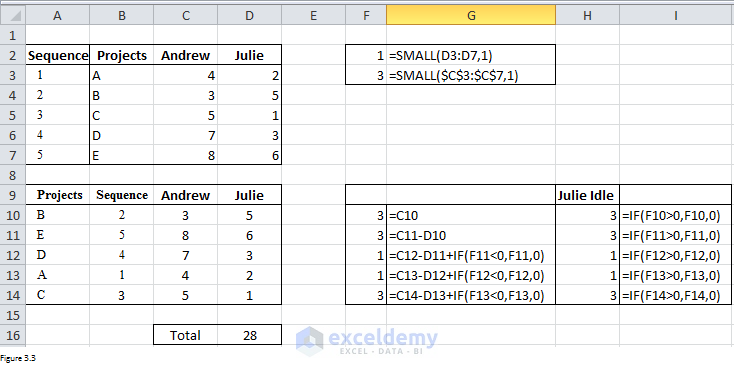
Figure 3.3
By comparing against results in the first part, you will find that results we just got and results got per Johnson’s rule are matched. It looks perfect. Now let’s move forward and see another case.
Read More: How to Use Solver in Excel (Solving Linear Programming Problems)!
Case 2: Get order of the tasks for companies
Problem
A company is faced with seven tasks that have to be processed through two work centers. Assume work “Center I” works continuously and that they are using Johnson’s rule. Data appear below in hours. What is the sequence of tasks?
| Projects | Center I | Center II |
| A | 2.58 | 3.47 |
| B | 1.66 | 5.84 |
| C | 2.71 | 2.41 |
| D | 5.52 | 1.99 |
| E | 3.38 | 7.62 |
| F | 5.22 | 1.73 |
| G | 2.89 | 1.11 |
Set up model
The way to set up a model for this problem is similar to that of case I. Range B12:B18 are ours by changing cells. VLOOKUP function was used to retrieve job names into range A12: A18 per the values of by changing cells. VLOOKUP function was also used to retrieve the time of each job into range C12:C18 and D12:D18 for work center A and work center B respectively.
Formulas used to get idle time were already listed in range G12:G18 and I12:I18. Our target cell is cell D20. SMALL function was used to retrieve two smallest times which will be used as constraints.
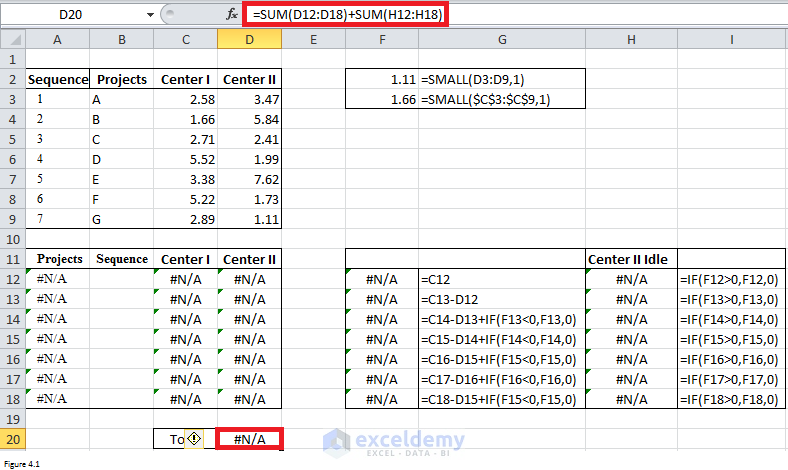
Figure 4.1
Fill Solver Parameter dialog box as shown in Figure 4.2.
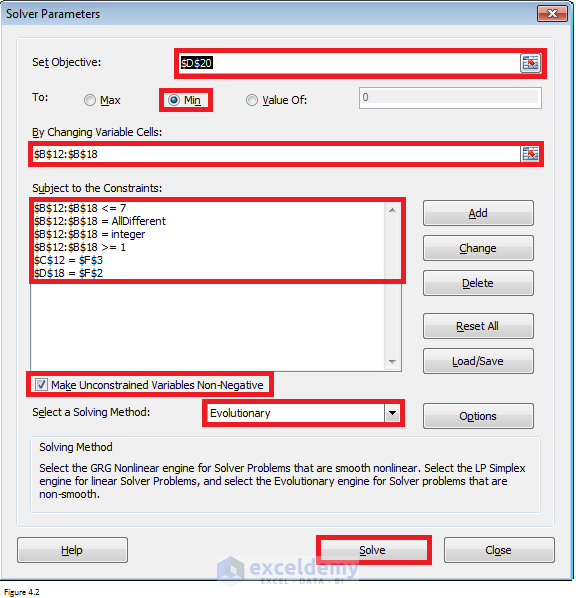
Figure 4.2
Results
After clicking on Solve, Excel will return the results as shown in Figure 4.3. The minimized makespan is 25.83 hours. And the total idle time for work center B is 1.66 hours.
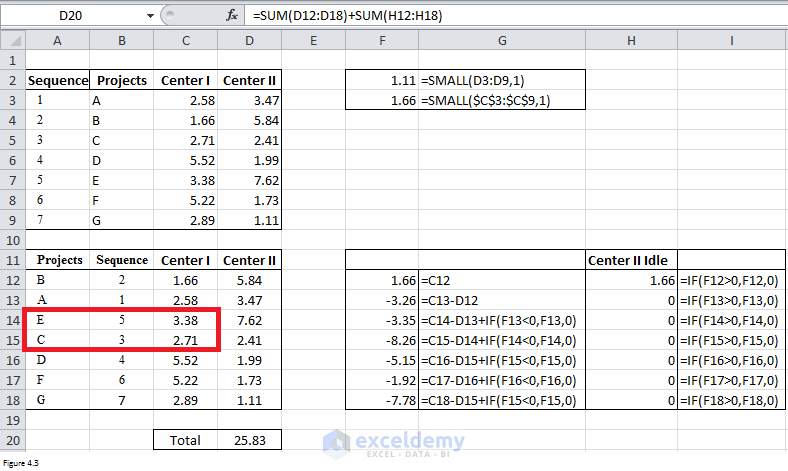
Figure 4.3
Well, if you look at results closely, you will find that value in cell C14 is greater than that in cell C15. This violates Johnson’s rule of putting smaller numbers first for work center A. You can try to add some constraints such as “C13 <= C14”, “C14<=C15”, “D17 <= D16” to force Excel to fix this problem automatically. But I cannot make sure that the constraints are always right or Solver can return a solution. Plus, it will take more time for Excel to return a solution. Therefore, I recommend you to manually change the sequence slightly.
Figure 4.4 shows the final results after I exchange cells C14 and C15. The minimized makespan is still 25.83. It is the final sequence that is the same as that solved per Johnson’s rule.
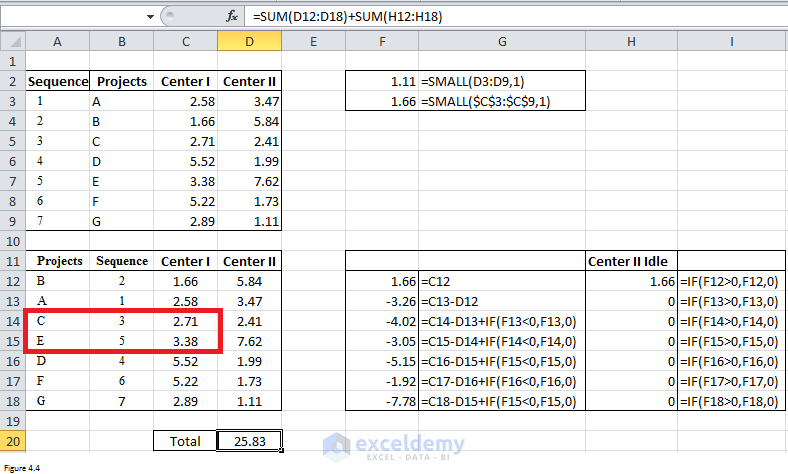
Figure 4.4





