3D Interpolation in Excel (with Easy Steps)

This article demonstrates the process of doing 3D interpolation in Excel. Basically, we have created a customized UDF (User-defined function) based on VBA to do this. More importantly, we have prepared a 3D graph based on the outputs.

3D interpolation in Excel is a powerful technique that enables users to estimate missing values or predict outcomes at unobserved data points within a three-dimensional grid. With its significance in data analysis, this method becomes a valuable tool for dealing with sparse datasets, whether they involve spatial data, time series, or any other three-dimensional data format. By using VBA code, users can bridge the gap between existing data points, gain a comprehensive understanding of their data, and make more informed decisions with confidence.

3D Interpolation in Excel: 4 Easy Steps

Let’s learn how to do 3D interpolation in Excel with 4 easy steps.

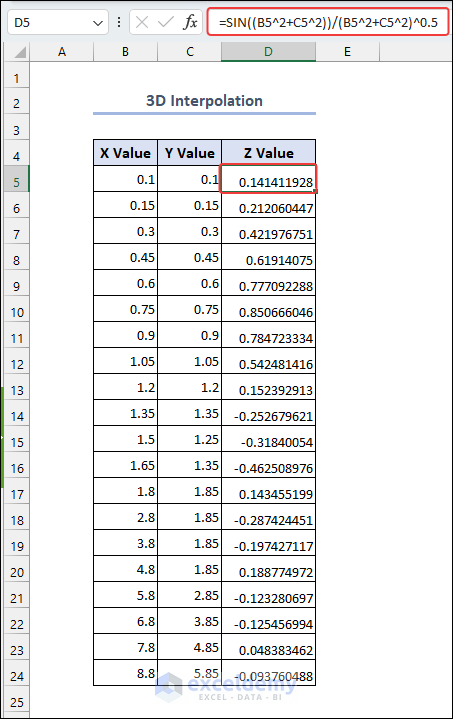
Step 1: Finding the Value of Z

First, we have to find out the value of the Z from the Z = SIN(x²+y²)/√(x²+y²) equation. To apply the equation, we have used the following formula in the D5 cell.

=SIN((B5^2+C5^2))/(B5^2+C5^2)^0.5

Here,

B5= X value
C5=Y value

The formula resembles Mexican Hat function. In the above formula, the SIN function returns the sine of given values.

Step 2: Creating UDF with VBA

Now, we are going to demonstrate how we have written the function.
First, we select Developer >> Visual Basic.

Select Insert >> Module.

We have to write down the code below.

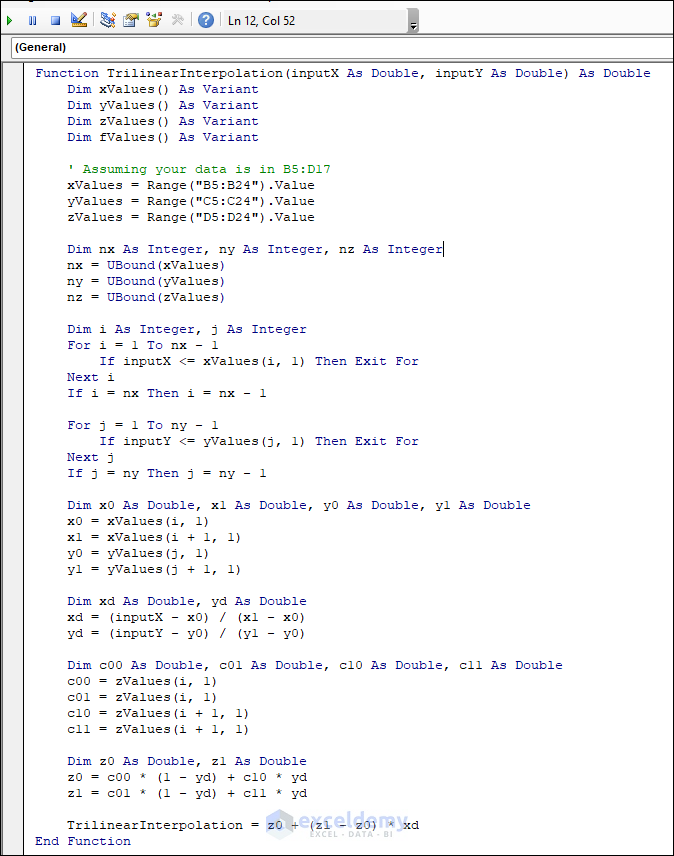
You can copy the code from here.

Function TrilinearInterpolation(inputX As Double, inputY As Double) As Double
    Dim xValues() As Variant
    Dim yValues() As Variant
    Dim zValues() As Variant
    Dim fValues() As Variant
    
    ' Assuming your data is in B5:D17
    xValues = Range("B5:B24").Value
    yValues = Range("C5:C24").Value
    zValues = Range("D5:D24").Value
    
    Dim nx As Integer, ny As Integer, nz As Integer
    nx = UBound(xValues)
    ny = UBound(yValues)
    nz = UBound(zValues)
    
    Dim i As Integer, j As Integer
    For i = 1 To nx - 1
        If inputX <= xValues(i, 1) Then Exit For
    Next i
    If i = nx Then i = nx - 1
    
    For j = 1 To ny - 1
        If inputY <= yValues(j, 1) Then Exit For
    Next j
    If j = ny Then j = ny - 1
    
    Dim x0 As Double, x1 As Double, y0 As Double, y1 As Double
    x0 = xValues(i, 1)
    x1 = xValues(i + 1, 1)
    y0 = yValues(j, 1)
    y1 = yValues(j + 1, 1)
    
    Dim xd As Double, yd As Double
    xd = (inputX - x0) / (x1 - x0)
    yd = (inputY - y0) / (y1 - y0)
    
    Dim c00 As Double, c01 As Double, c10 As Double, c11 As Double
    c00 = zValues(i, 1)
    c01 = zValues(i, 1)
    c10 = zValues(i + 1, 1)
    c11 = zValues(i + 1, 1)
    
    Dim z0 As Double, z1 As Double
    z0 = c00 * (1 - yd) + c10 * yd
    z1 = c01 * (1 - yd) + c11 * yd
    
    TrilinearInterpolation = z0 + (z1 - z0) * xd
End Function

🔎 Code Explanation

Function Definition: The code defines a function called TrilinearInterpolation that takes two input arguments (inputX and inputY) of type Double and returns a Double value as the result of the trilinear interpolation.

Function TrilinearInterpolation(inputX As Double, inputY As Double) As Double

Declaring Variables: Several arrays (xValues, yValues, zValues, and fValues) and other variables are declared to hold the input data and intermediate values during the interpolation process.

Dim xValues() As Variant
    Dim yValues() As Variant
    Dim zValues() As Variant
    Dim fValues() As Variant

Assigning Data: The code assumes that the data for the interpolation is stored in the range B5:D24 of the Excel sheet. The data in columns B, C, and D is copied into the respective arrays (xValues, yValues, and zValues) using the Range().Value method.

   xValues = Range("B5:B24").Value
    yValues = Range("C5:C24").Value
    zValues = Range("D5:D24").Value

Determining Array Sizes: The variables nx, ny, and nz are used to store the upper bound of the arrays xValues, yValues, and zValues, respectively. These values represent the number of data points available along each axis.

Dim nx As Integer, ny As Integer, nz As Integer
    nx = UBound(xValues)
    ny = UBound(yValues)
    nz = UBound(zValues) 
    Dim i As Integer, j As Integer
    For i = 1 To nx - 1
        If inputX <= xValues(i, 1) Then Exit For
    Next i
    If i = nx Then i = nx - 1
    For j = 1 To ny - 1
        If inputY <= yValues(j, 1) Then Exit For
    Next j
    If j = ny Then j = ny - 1

Finding the Interval for X: The code uses a loop to find the interval where inputX falls between xValues(i, 1) and xValues(i+1, 1). It iterates over the array xValues and compares inputX with each element until it finds the interval where inputX lies. It then stores the index i representing the lower bound of the interval. If inputX is greater than or equal to the last element of xValues, i is set to nx – 1.

   Dim x0 As Double, x1 As Double, y0 As Double, y1 As Double
    x0 = xValues(i, 1)
    x1 = xValues(i + 1, 1)

Finding the Interval for Y: Similarly, the code uses another loop to find the interval where inputY falls between yValues(j, 1) and yValues(j+1, 1). It iterates over the array yValues and compares inputY with each element until it finds the interval where inputY lies. It then stores the index j representing the lower bound of the interval. If inputY is greater than or equal to the last element of yValues, we set j to ny – 1.

y0 = yValues(j, 1)
 y1 = yValues(j + 1, 1)

Calculating Interpolation Parameters: The code calculates interpolation parameters xd and yd for inputX and inputY, respectively. xd represents the relative position of inputX within the interval determined by xValues(i, 1) and xValues(i+1, 1). Similarly, yd represents the relative position of inputY within the interval determined by yValues(j, 1) and yValues(j+1, 1).

Dim xd As Double, yd As Double
    xd = (inputX - x0) / (x1 - x0)
    yd = (inputY - y0) / (y1 - y0)
    Dim c00 As Double, c01 As Double, c10 As Double, c11 As Double
    c00 = zValues(i, 1)
    c01 = zValues(i, 1)
    c10 = zValues(i + 1, 1)
    c11 = zValues(i + 1, 1)

Calculating Interpolation for Z: The code uses the trilinear interpolation method to calculate z0 and z1 by combining data from four corners of a cube formed by c00, c01, c10, and c11. These corner values are the zValues corresponding to the positions (x0, y0), (x0, y1), (x1, y0), and (x1, y1) respectively. The z0 and z1 values are calculated using bilinear interpolation in the x-y plane.

 Dim z0 As Double, z1 As Double
    z0 = c00 * (1 - yd) + c10 * yd
    z1 = c01 * (1 - yd) + c11 * yd

Final Trilinear Interpolation: The code calculates the final result using xd to interpolate between z0 and z1. This step combines the interpolated values from the x and y directions to obtain the final interpolated value for the given inputX and inputY. The result is assigned to the function and returned as the output of the TrilinearInterpolation function.

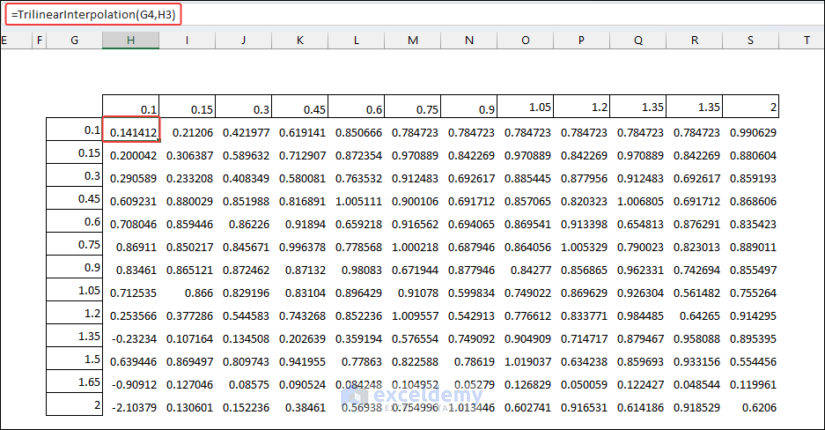
Step 3: Prepare Dataset According to X and Y value

Already we created a TrilinearInterpolation function using VBA to create 3D interpolation from the dataset. Now, it’s time to apply the function. So, the formula will be in the H4

=Trilinearinterpolation(G4,H3)

Here,

G4= X values, and H3=Y values.

Step 4: Create 3D Interpolation Graph

To get a better visualization of the outputs, we can create a 3D graph.

Select the data and click on Recommend Charts.

Next, select All Charts >> choose Surface >> pick 3D Surface chart >> finally, press OK.

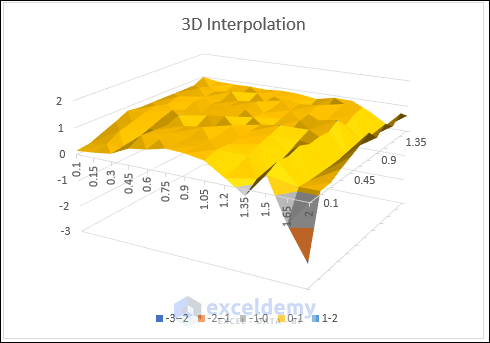
Now, we will get the interpolated 3D graph.

Things to Remember

Take more data points for your function so it can predict all the data well.
Whenever possible, compare the interpolated results with actual data points to validate the accuracy of your interpolation. This step is essential to ensure the reliability of your predictions.

Frequently Asked Questions

1. What are the benefits of 3D interpolation in Excel?

3D interpolation allows users to fill in missing data points within a dataset, enabling a more complete analysis and visualization. It helps in making accurate predictions and provides a smoother representation of the data, particularly when dealing with sparse datasets.

2. How can I deal with outliers or noisy data in 3D interpolation?

Handling outliers or noisy data is crucial for accurate 3D interpolation. Preprocessing techniques such as data smoothing, data filtering, or outlier removal, we can apply before interpolation to improve the reliability of results.

Download Practice Workbook

3d Interpolation.xlsm

Conclusion

In conclusion, the use of VBA code for 3D interpolation in Excel represents a significant achievement in data analysis and visualization. By enabling the estimation of missing values and predicting outcomes within a three-dimensional dataset, this customized and dynamic approach adds a valuable tool to the Excel user’s repertoire. The ability to perform advanced interpolation empowers users to gain deeper insights and make more informed decisions, making it an essential asset for data analysts and researchers.

<< Go Back to Excel Interpolation | Excel for Statistics | Learn Excel

Get FREE Advanced Excel Exercises with Solutions!