How to Apply Cubic Spline Interpolation in Excel (with Easy Steps)

When it comes to software, Microsoft Excel is in a league of its own. Thanks to its many useful features, we may fully use any data. This article will cover how we can use Excel VBA to interpolate Cubic Spline from start to finish here. Cubic Spline Interpolation is a curve-fitting method to interpolate a smooth curve between discrete data points. We use this Interpolation in various applications due to its ability to model smooth and continuous curves that pass through all the data points while being computationally efficient and easy to implement. 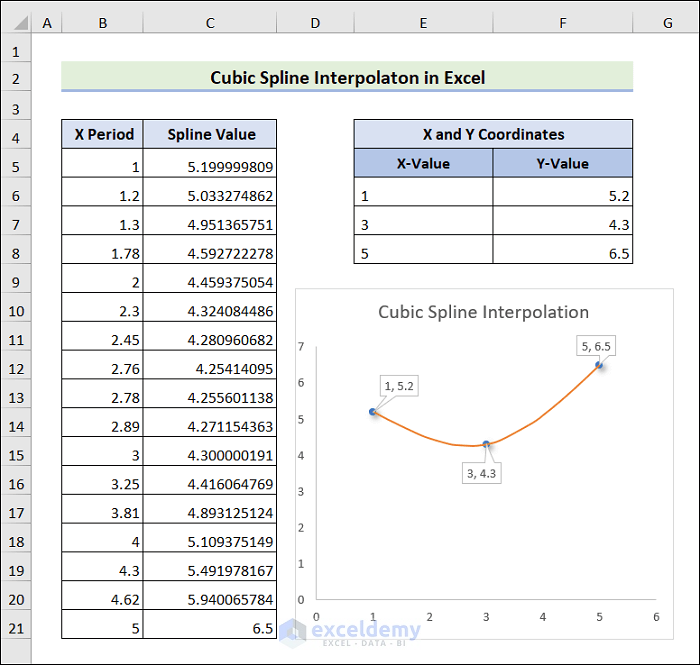Keeping this in mind, we’ll look at the specific steps for using Cubic Spline Interpolation in Excel.

What Is Cubic Spline Interpolation?

Cubic Spline Interpolation is constructing a smooth curve that passes through a given set of data points. It uses a set of cubic polynomials to represent the curve, ensuring that the resulting curve is smooth and has continuous first and second derivatives. We need cubic spline interpolation because we often have a set of discrete data points that need to be transformed into a continuous function in real-world applications. Cubic spline interpolation provides a smooth curve representing this continuous function and making predictions or estimates at unavailable data.

Cubic Spline Interpolation in Excel: Step-by-Step Procedure

If we know the proper steps, it can be easy to interpolate Cubic Spline in Excel. This post will show how you can use the VBA language to display the Interpolation of Cubic Spline in 5 steps. In the first step, we will organize the Data Model. Later, we will insert the required value into the model. We’ll write VBA code throughout the following step to create a User-Defined function to determine the interpolated values. In the next step, we’ll discuss plotting the graph using the values produced from the user-defined function. Follow these steps carefully to figure out how to do something quickly.

Step 1: Set up Data Model for Cubic Spline Interpolation

The first and foremost step is to create a dataset for illustration purposes. In this article, we will consider the dataset having two columns titled X Period, Spline Value. We also have two sub-columns named X-Value and Y-Value. These belong to X and Y Coordinates. Please follow the steps below to make the model.

First, build X Period and Spline Value columns throughout B and C.
Later, take another section called X and Y Coordinates in the E and F columns.
Here, column E represents X-Value, and column F contains Y-Value.

Step 2: Input Required Data into Cubic Spline Model

In this context, we will insert the necessary values into the model. Firstly, we input the X-Value and Y-Value columns. We also have to provide the data for X Period.

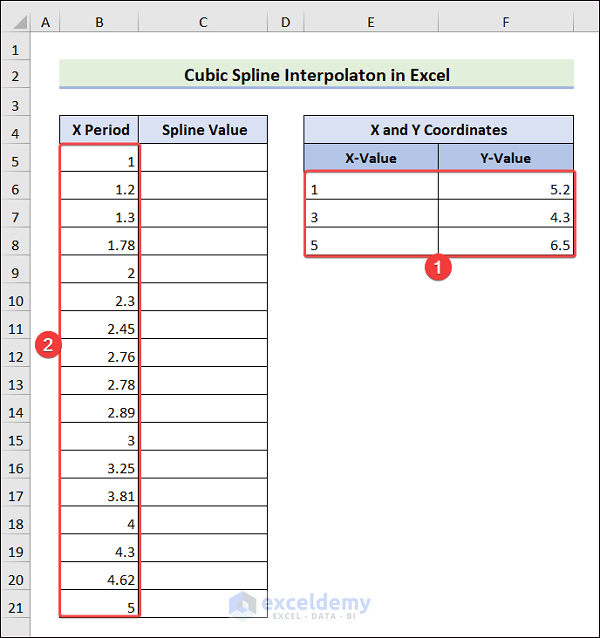
Initially, insert the intended values in the X-Value and Y-Value columns.
After that, input the desired values for the X Period column like the following.

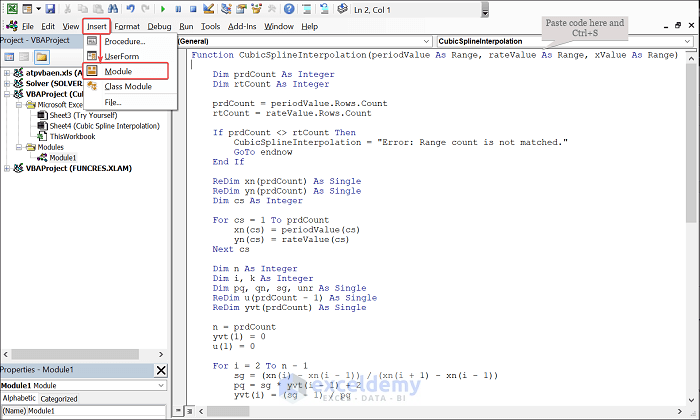
Step 3: Utilize Excel VBA Code to Build a User-Defined Function

The acronym VBA stands for Visual Basic for Application, and Microsoft created VBA as its programming language. Users can access Excel-incompatible functionalities by utilizing the VBA programming language. In this section, we will use the VBA to make a User-Defined function in Excel called CubicSplineInterpolation. Please read the instructions carefully and follow them to accomplish the task.

First, press ALT + F11 to open VBA Editor.
Next, choose Insert followed by Module and paste the below code.

Function CubicSplineInterpolation(periodValue As Range, rateValue As Range, xValue As Range)

Dim prdCount As Integer
Dim rtCount As Integer

prdCount = periodValue.Rows.Count
rtCount = rateValue.Rows.Count

If prdCount <> rtCount Then
CubicSplineInterpolation = "Error: Range count is not matched."
GoTo endnow
End If

ReDim xn(prdCount) As Single
ReDim yn(prdCount) As Single
Dim cs As Integer

For cs = 1 To prdCount
xn(cs) = periodValue(cs)
yn(cs) = rateValue(cs)
Next cs

Dim n As Integer
Dim i, k As Integer
Dim pq, qn, sg, unr As Single
ReDim u(prdCount - 1) As Single
ReDim yvt(prdCount) As Single

n = prdCount
yvt(1) = 0
u(1) = 0

For i = 2 To n - 1
sg = (xn(i) - xn(i - 1)) / (xn(i + 1) - xn(i - 1))
pq = sg * yvt(i - 1) + 2
yvt(i) = (sg - 1) / pq
u(i) = (yn(i + 1) - yn(i)) / (xn(i + 1) - xn(i)) - (yn(i) - yn(i - 1)) / (xn(i) - xn(i - 1))
u(i) = (6 * u(i) / (xn(i + 1) - xn(i - 1)) - sg * u(i - 1)) / pq

Next i

qn = 0
unr = 0
yvt(n) = (unr - qn * u(n - 1)) / (qn * yvt(n - 1) + 1)

For k = n - 1 To 1 Step -1
yvt(k) = yvt(k) * yvt(k + 1) + u(k)
Next k

Dim kl, kh As Integer
Dim hn, bcs, asp As Single

kl = 1
kh = n

Do
k = kh - kl
If xn(k) > xValue Then
kh = k
Else
kl = k
End If
k = kh - kl
Loop While k > 1
hn = xn(kh) - xn(kl)
asp = (xn(kh) - xValue) / hn
bcs = (xValue - xn(kl)) / hn
yFinal = asp * yn(kl) + bcs * yn(kh) + ((asp ^ 3 - asp) * yvt(kl) + (bcs ^ 3 - bcs) * yvt(kh)) * (hn ^ 2) / 6

CubicSplineInterpolation = yFinal

endnow:
End Function

Now, press Ctrl + S or click the Save icon.

Step 4: Determine Interpolate Y Value Using User-Defined Function in Excel

At this point, we will call the function we previously developed and determine the Interpolated Y value (Spline Value) to plot a smooth graph. Please read the directions thoroughly and stick to them to complete the work.

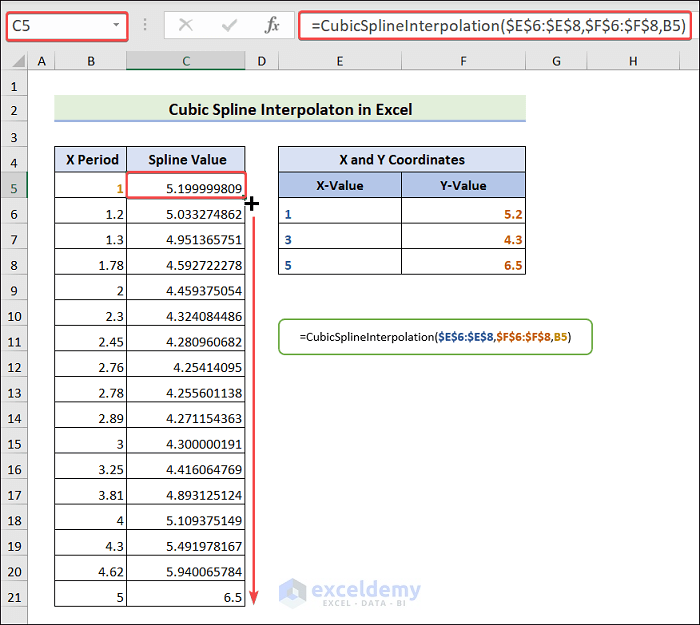
Select the C5 cell and apply the equation below in the Formula bar.

=CubicSplineInterpolation($E$6:$E$8,$F$6:$F$8,B5)

After that, hit the Enter key and drag the Fill Handle icon to C21.
As a result, we get the desired output like the below one.

Step 5: Display Chart Data for Cubic Spline Interpolation in Excel

Finally, we can plot the intended graph after getting the Spline Value. Here, we will consider the Scatter with Smooth Lines to graph the values.

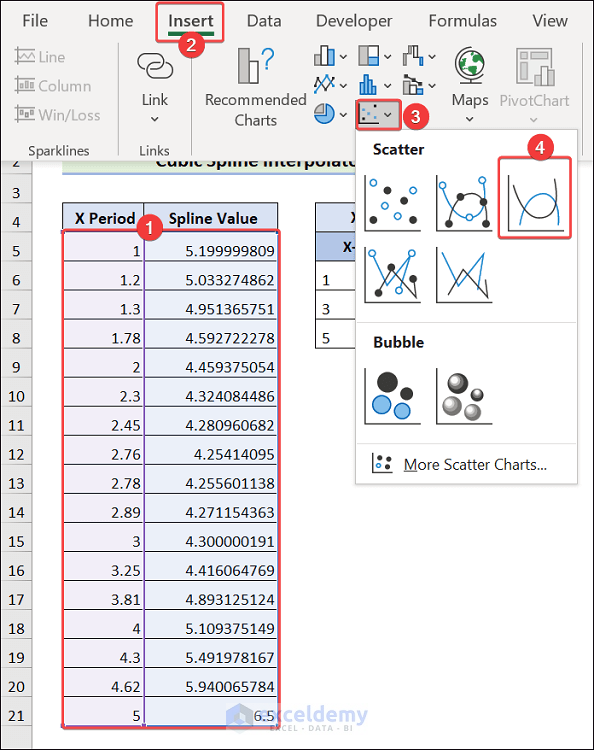
To begin, select range B5:C21 and go to the Insert tab.
Now click on the Scatter Chart followed by Scatter with Smooth Lines.

As a result, it will display the Cubic Spline Interpolation like the following.

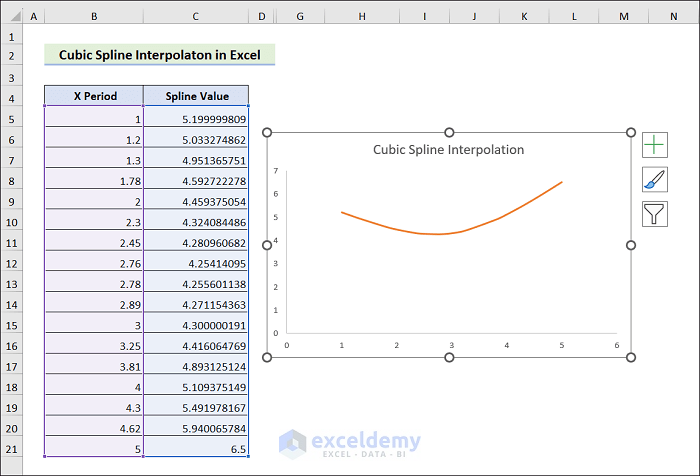
Insert the X and Y Coordinates into the previous chart to verify the interpolation.

Things to Remember

The User-Defined function can malfunction if the X Period columns contain a value that crosses the upper and lower boundaries of the X-Value.
While saving the workbook, ensure to keep it as the macro-enabled workbook.

Download Practice Workbook

Please click the link below this section if you’d like a free copy of the sample workbook discussed in the presentation.

Cubic Spline Interpolation.xlsm

Conclusion

Following the above instructions will allow you to use the Cubic Spline Interpolation in Excel. Please share any additional recommendations or enhanced methods as you continue to apply them. Include your opinions, questions, and requests in the allocated area.

Get FREE Advanced Excel Exercises with Solutions!

6 Comments

jay dee Apr 8, 2023 at 2:06 AM

interest in robotic math in excell
- Reply
  Shamima Sultana Apr 9, 2023 at 9:32 AM
  
  Dear Jay Dee,
  
  That’s good to hear. We are interested to know more from you.
  
  Regards
  ExcelDemy
Torsten Apr 15, 2023 at 1:40 PM

This interpolation is not correct! The orange Line has to hit the given dots of the blue line as aminimum requirement! Otherwise its not an interpolation at all!

Please check the formulas! Seems to be a mistake somewhere.
- Reply
  Alif Bin Hussain Apr 25, 2023 at 3:37 PM
  
  Hello Torsten,
  
  Thank you for bringing this matter to our attention. We will look into the VBA function to see if it can be updated to minimize the deviation of the orange line from the given points.
  
  Besides, I would like to address your concern regarding interpolation methods. There are some interpolation methods that go through all the given points such as Lagrange interpolation or polynomial interpolation etc. However, interpolation method such as cubic spline interpolation does not necessarily pass through all the given data points.
Dustin Oct 20, 2023 at 4:26 PM

How would you add a smoothing option, either directly into the VB code or via function, with the option to define “p”. For example

https://www.mathworks.com/help/curvefit/smoothing-splines.html
- Reply
  Lutfor Rahman Shimanto Oct 22, 2023 at 2:44 PM
  Hello DUSTIN
  
  Thanks for reaching out and posting your query. You want to add a smoothing option while interpolating. You can achieve the goal with Excel formulas. However, I am presenting an Excel VBA User-defined function where you can add a smoothing option.
  
  Assume you have two user-defined functions for applying the Cubic Spline and Cubic Hermite Spline interpolations. You want to create another user-defined function that will have the same parameters as before, including another extra parameter for choosing the smoothing option. Let’s say if p is provided, it will apply the Cubic Spline interpolation. And if q is provided, it will apply the Hermite Spline interpolation. If the Choose Parameter is not provided, it will raise a warning.
  
  Excel VBA Code:
```
Function InterpolateWithChoice(periodValue As Range, rateValue As Range, xValue As Range, choice As String) As String
    
    If choice = "p" Then
        InterpolateWithChoice = CubicSplineIntrp(periodValue, rateValue, xValue)
    ElseIf choice = "q" Then
        InterpolateWithChoice = HrmtSplines(periodValue, rateValue, xValue)
    Else
        MsgBox "Invalid Choice! Please use 'p' for Cubic Spline or 'q' for Hermite Spline.", vbExclamation, "Invalid Choice"
        InterpolateWithChoice = "#Invalid Choice"
    End If

End Function

Function CubicSplineIntrp(periodValue As Range, rateValue As Range, xValue As Range)
    CubicSplineIntrp = "Cubic Spline"
End Function

Function HrmtSplines(periodValue As Range, rateValue As Range, xValue As Range)
    HrmtSplines = "Hermite Spline"
End Function
```
  OUTPUT:
  
  1. Cubic Spline
  Here, we are providing p as the Choose Parameter.
  
  2. Hermite Spline
  We are providing q as the Choose Parameter.
  
  3. Error Handling
  Now, we are not providing any of the Choose Parameters. As a result, a Warning Window appears.
  
  Press OK => You will get an output like the following image.
  
  Hopefully, the idea will help you. Good luck!
  
  Regards
  Lutfor Rahman Shimanto