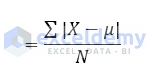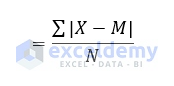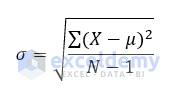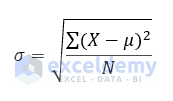In Excel, Deviation is a measure of how spread out your data is. A large deviation means that your data is more spread out; a small deviation means it’s more clustered. There are many kinds of deviation in Excel. In this article, I am going to show how to calculate the mean and standard deviation in Excel. I hope it will be very helpful for you if you are searching for the process of mean and standard deviation calculation.
Introduction to Mean Deviation
What Is Mean Deviation?
Mean Deviation is a statistical measure of variability. It is calculated as the average of the absolute deviations of the data from the mean. To calculate the mean deviation in Excel, first, calculate the mean of your data set using the AVERAGE function.
Then, use the ABS function to take the absolute value of the difference between each data point and the mean. Finally, take the average of those absolute values using the AVERAGE function.
The data values are concentrated closer together when the mean absolute deviation has a low value. A high mean absolute deviation score indicates that the data values are more widely distributed.
Arithmetic Formula to Calculate Mean Deviation
The mean deviation can be calculated as the mean deviation from the mean or the mean deviation from the median. If in your calculation the arithmetic mean is subtracted from the individual values then it is called the mean deviation from the mean. If the subtracted item is the median then it is called the mean deviation from the median. The formulas for calculating the mean deviation are given below.
Mean Deviation from Mean
Where,
- X is each observation
- μ is the arithmetic mean
- N is the total number of observations
Mean Deviation from Median
Where,
- X is each observation
- M is the Median of the observations
- N is the total number of observations
Introduction to Standard Deviation
What Is Standard Deviation?
Standard Deviation is a statistical measure of dispersion, or how spread out data is. It is calculated as the square root of the variance. The variance is the average of the squared differences from the mean. Its symbol is σ (the greek letter sigma).
Arithmetic Formula to Calculate Standard Deviation
To calculate the standard deviation, you need to calculate the variance first as the standard deviation is the square root of the variance. The standard deviation can be of 2 kinds. They are population standard deviation and sample standard deviation. The formula for calculating the standard deviation is given below.
Population Standard Deviation
Sample Standard Deviation
Here for both equations,
- μ is the arithmetic mean
- X is the individual value
- N is the size of the population
- σ is the standard deviation
Basic Examples to Calculate Mean and Standard Deviation in Excel
Mean Deviation Calculation with Formula
In order to calculate Mean Deviation in Excel, we just need to follow the following steps sequentially.
Steps:
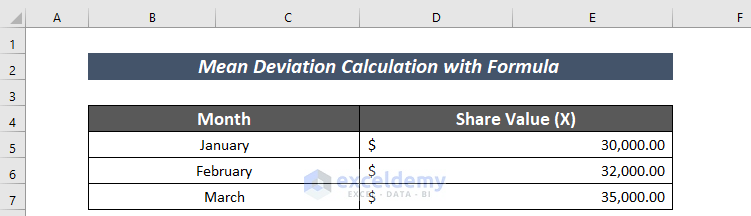
- Organize a dataset first. Here, I have taken a dataset on share values in different months of the year.
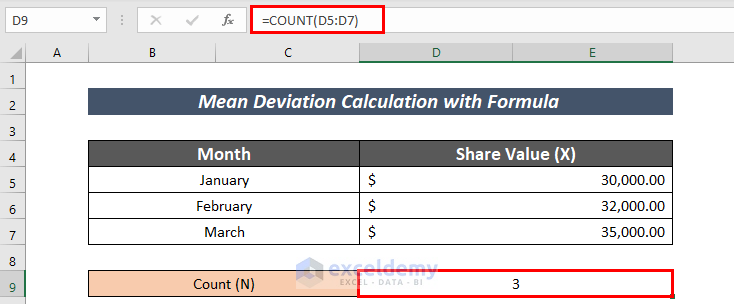
- Next, apply the following formula to count the number of values.
=COUNT(D5:D7)Here, The COUNT function counts the number of values in cell D5:D7.
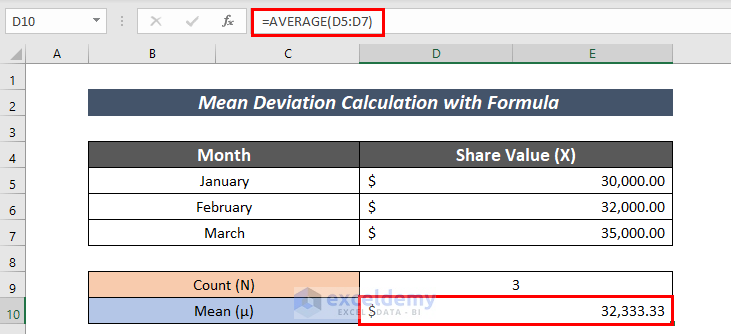
- Input the following formula to calculate the Mean.
=AVERAGE(D5:D7)Here, the AVERAGE function calculates the mean in the range D5:D7.
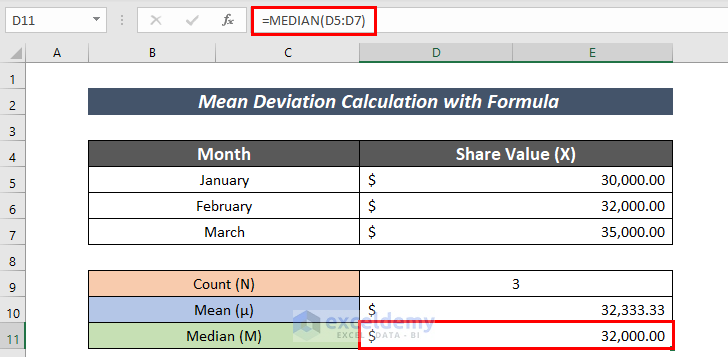
- Calculate the Median using the following formula:
=MEDIAN(D5:D7)Here, the MEDIAN function calculates the median in the range D5:D7.
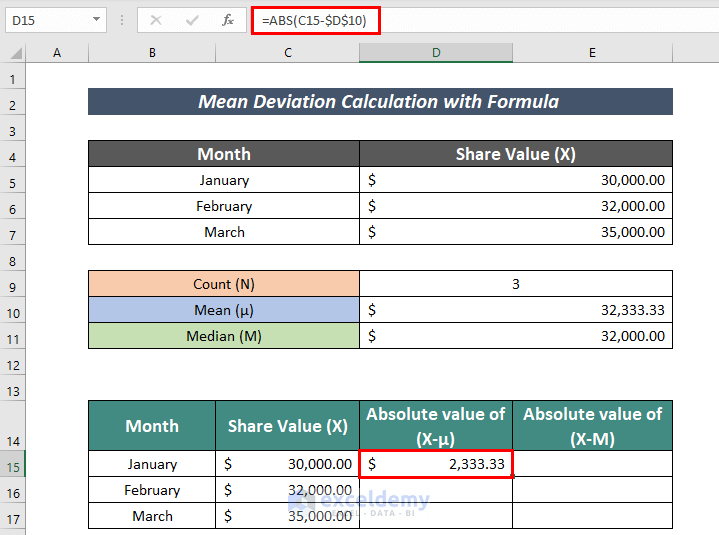
- Now, calculate the absolute value of the difference between the share value and the mean value.
=ABS(C15-$D$10)Here,
C15 = Share value
D10 = Mean Value
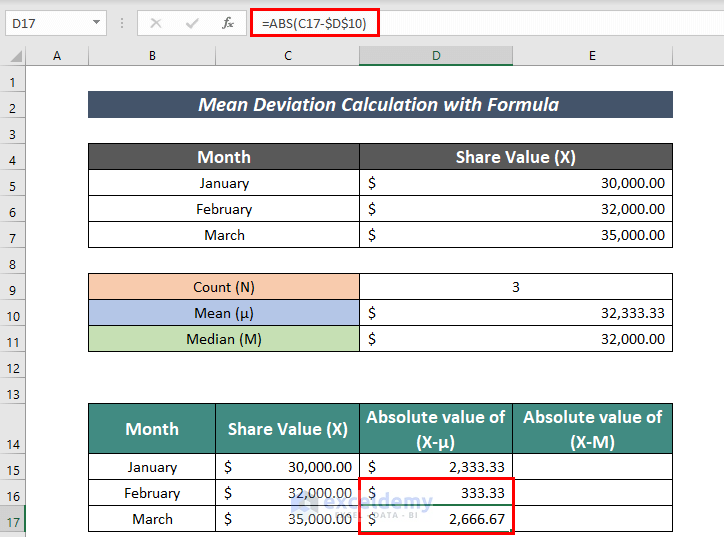
- Use Fill Handle to AutoFill the rest cells.
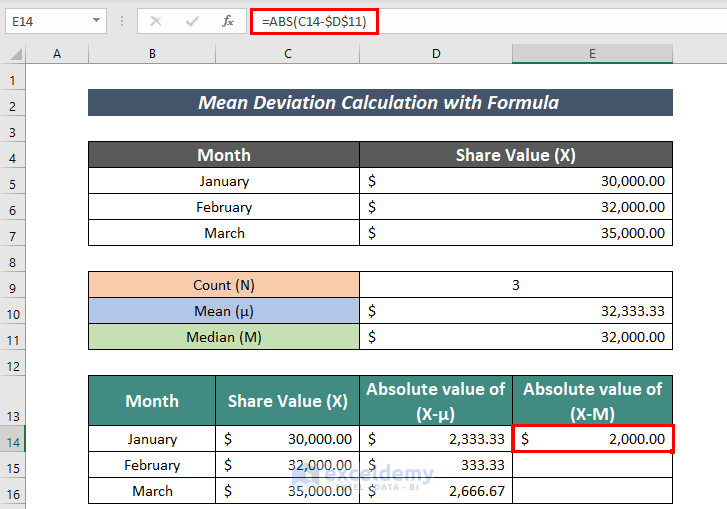
- Similarly, calculate the absolute value of the difference between the share value and the median value.
=ABS(C14-$D$11)Here,
C14 = Share value
D11 = Median Value
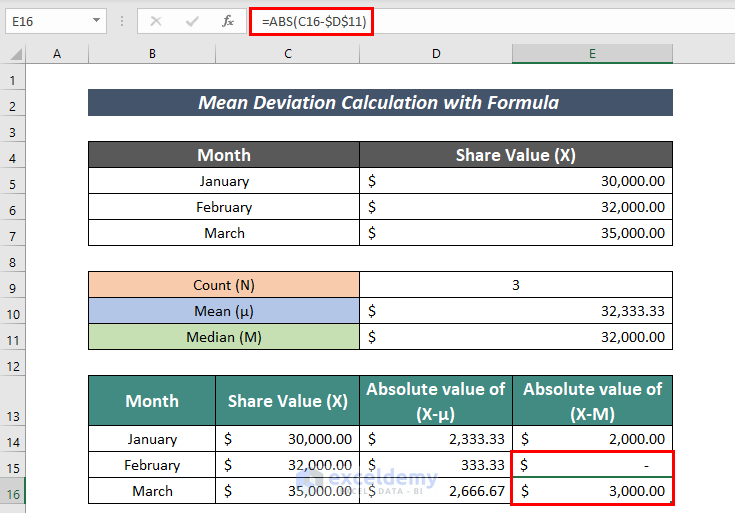
- AutoFill the rest cells.
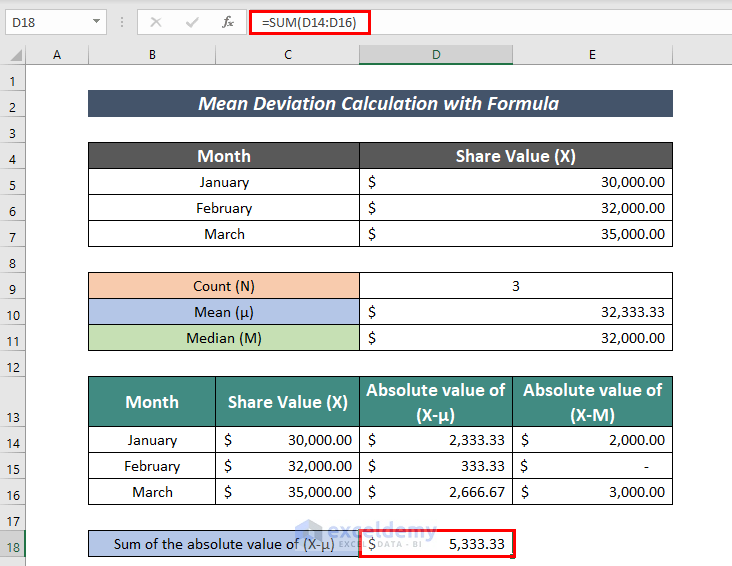
- After that, calculate the Sum of the absolute value of (X-μ). For that, the formula is:
=SUM(D14:D16)The SUM function here adds the value in the cells D14:D16.
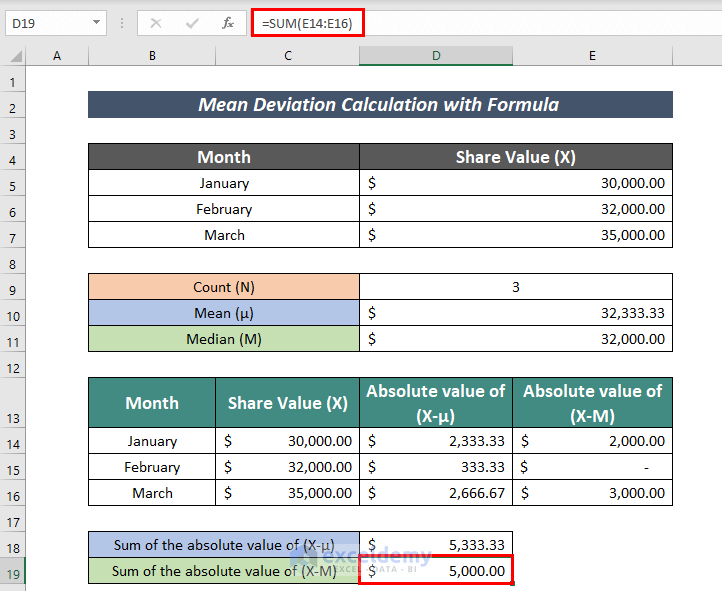
- Next, calculate the Sum of the absolute value of (X-M) using the below-mentioned formula:
=SUM(E14:E16)The SUM function here adds the value in the cells E14:E16.
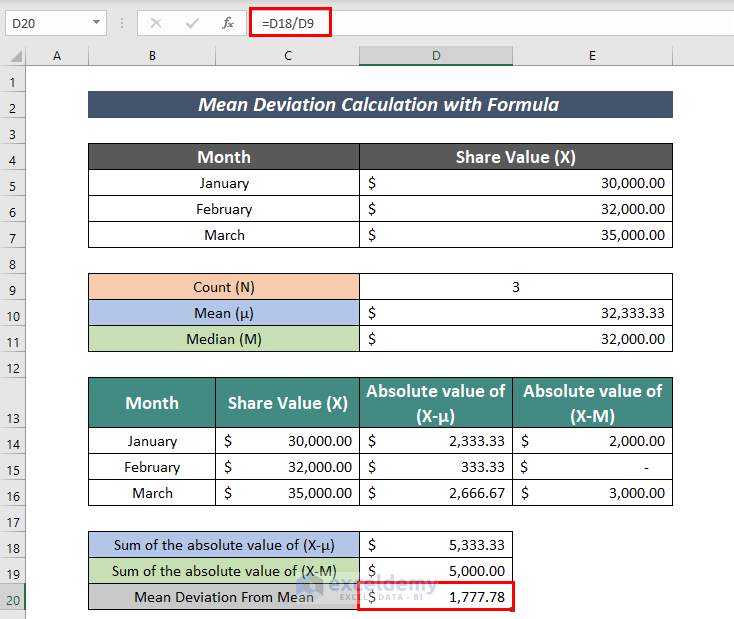
- Along with this, apply the following formula to calculate Mean Deviation From Mean:
=D18/D9Here,
D18 = Sum of the absolute value of (X-μ)
D9 = Number of Share Values
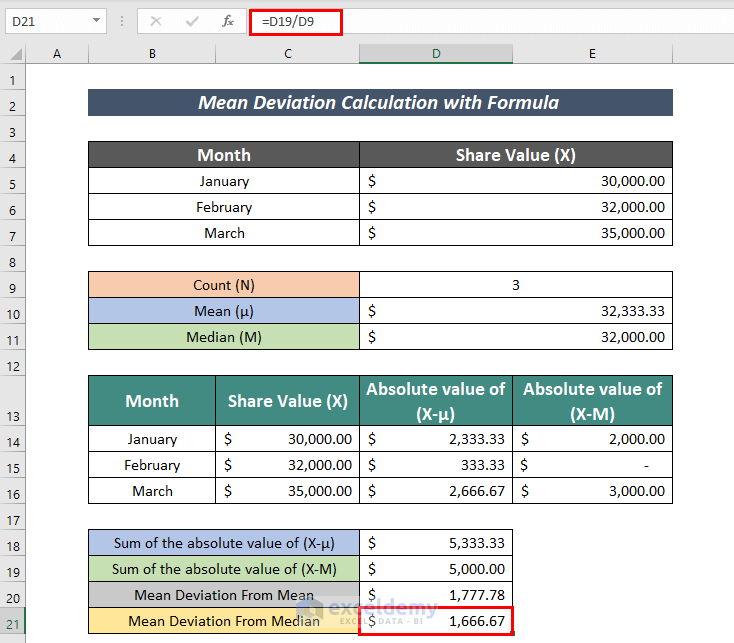
- Lastly, apply the following formula to calculate the Mean Deviation From the Median:
=D19/D9Here,
D19 = Sum of the absolute value of (X-M)
D9 = Number of Share Values
Thus, we can calculate both Mean Deviation from Mean and Median.
Standard Deviation Calculation with Formula
We just need to follow the following steps sequentially in order to calculate Standard Deviation in Excel.
Steps:
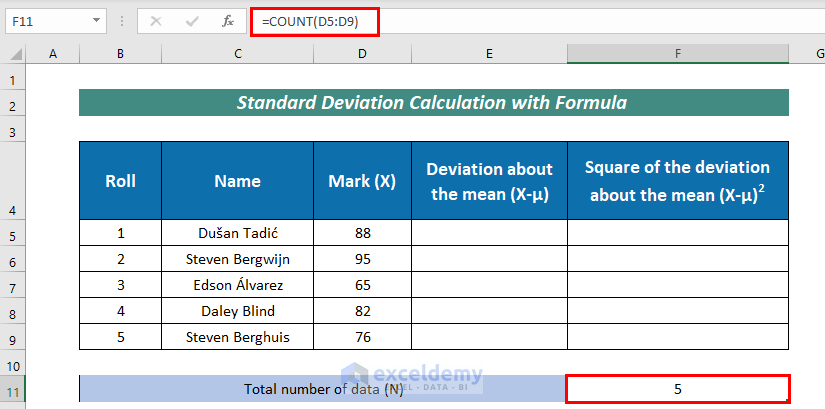
- Firstly, organize a dataset with related information. Here, I have arranged examination marks in Roll, Name, and Mark (X) columns.
- Next, apply the following formula to calculate Total number of data (N):
=COUNT(D5:D9)Here, the COUNT function returns the number of frequencies in cell D5:D9.
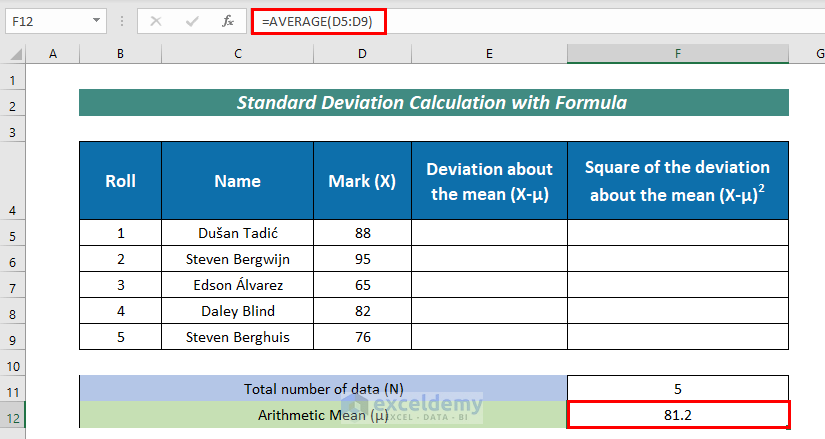
- Now, apply the following formula to calculate the Arithmetic Mean (μ):
=AVERAGE(D5:D9)Here, the AVERAGE function calculates the mean in the range D5:D9.
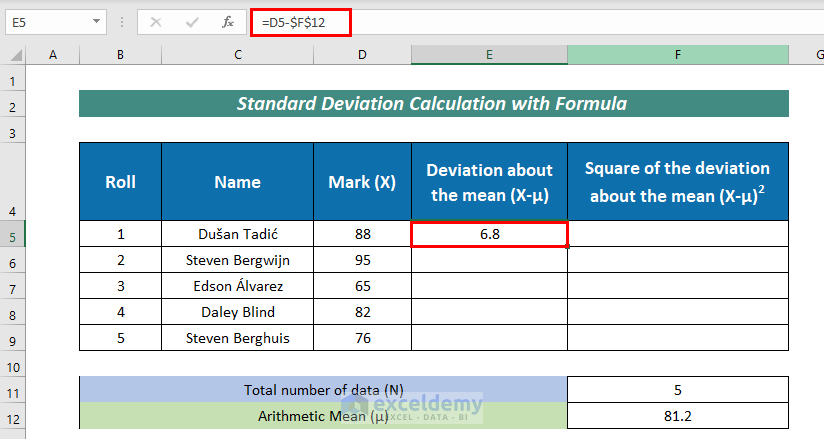
- After that, calculate the Deviation about the mean (X-μ) with the formula mentioned below:
=D5-$F$12Here,
D5 = frequency value
F12 = Arithmetic Mean
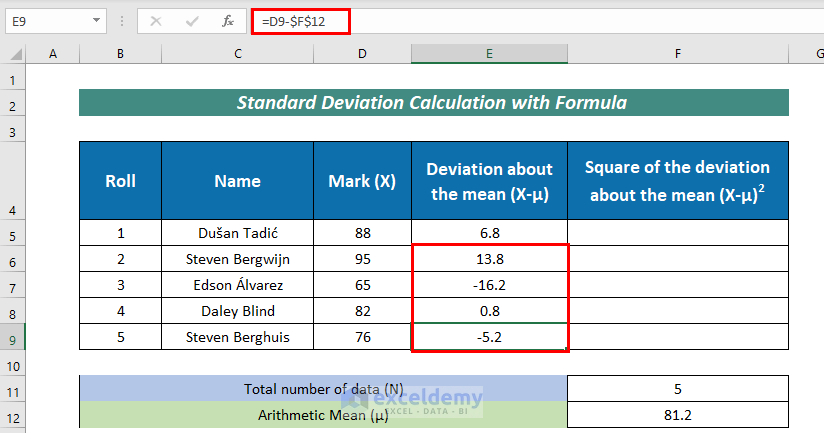
- Then, AutoFill the remaining cells.
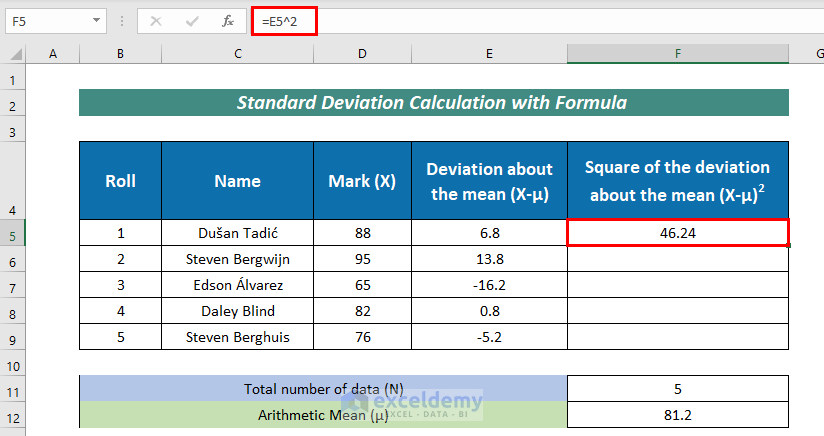
- Again, calculate the Square of the deviation about the mean (X-μ)^2 with the formula mentioned below:
=E5^2Here, I simply squared the value in cell E5 which is a Deviation of the mean (X-μ).
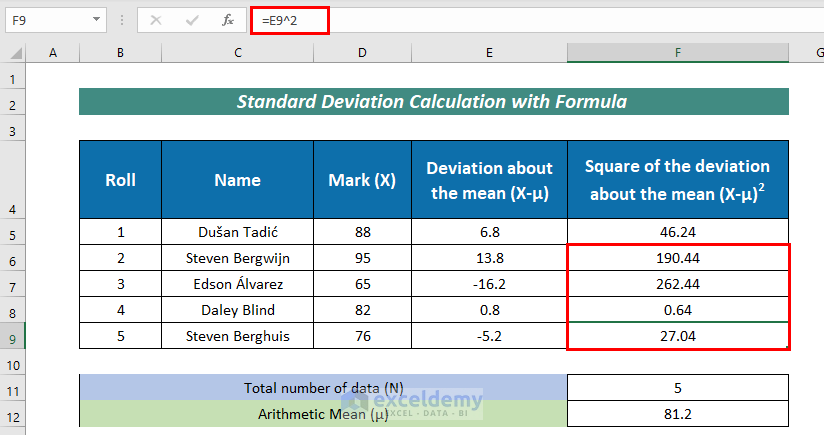
- AutoFill the rests.
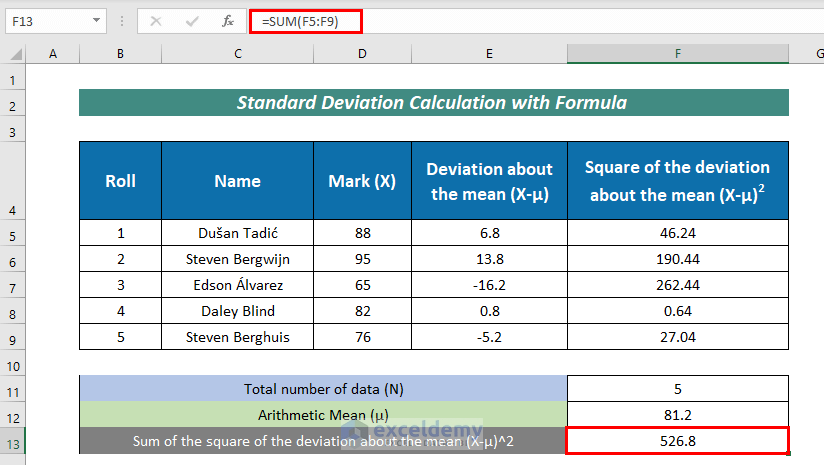
- Afterward, find the Sum of the square of the deviation about the mean (X-μ)^2 with the formula:
=SUM(F5:F9)Here, The SUM function added the value in cells F5:F9.
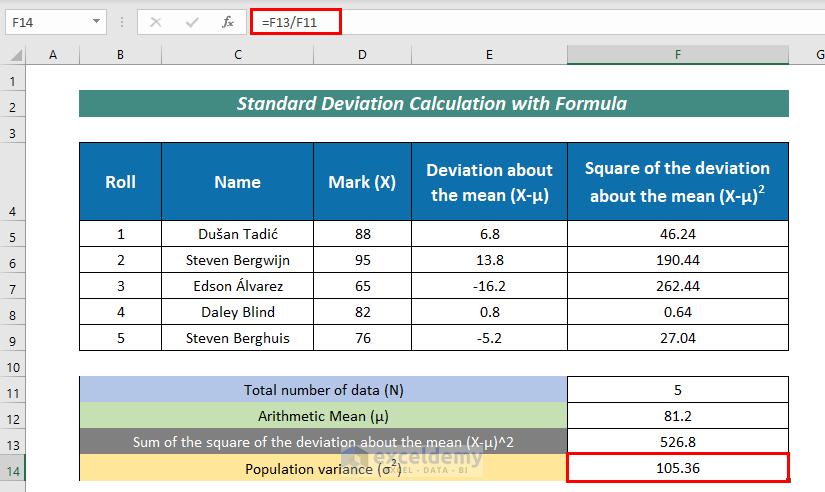
- Along with that, measure Population variance (σ^2) with the following formula:
=F13/F11Here,
F13 = Sum of the square of the deviation about the mean (X-μ)^2
F11 = Total number of data
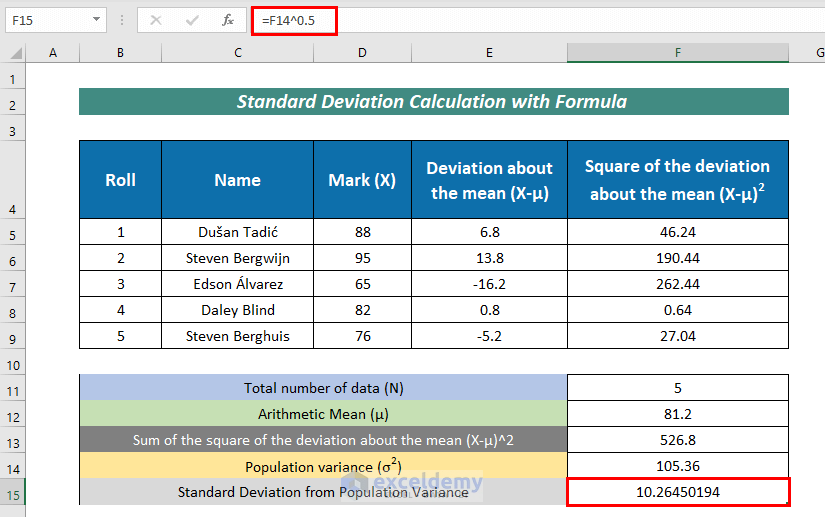
- Next, apply the following formula to calculate Standard Deviation from Population Variance:
=F14^0.5Here, F14 defines Population variance.
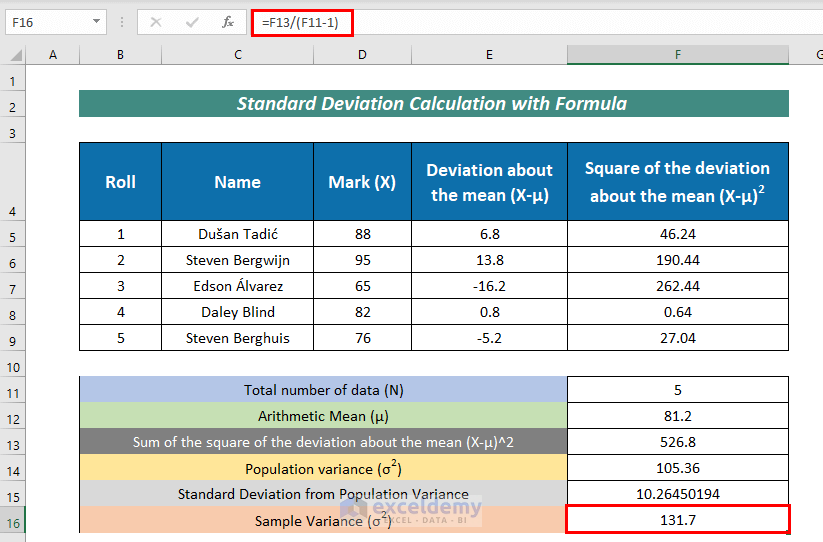
- To find Sample Variance (σ^2), input the following formula:
=F13/(F11-1)Here,
F13 = Sum of the square of the deviation about the mean (X-μ)^2
F11 = Total number of data
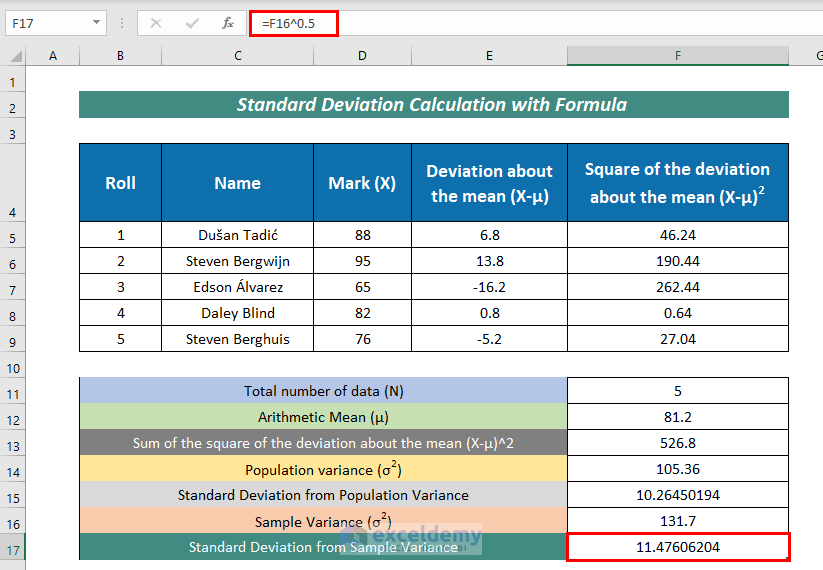
- Finally, input the following formula to have Standard Deviation from Sample Variance:
=F16^0.5Here, F16 represents Sample Variance.
Read More: How to Calculate Standard Deviation with IF Conditions in Excel
Calculating Mean and Standard Deviation Using Built-in Excel Functions
There are some built-in functions in Excel to calculate Mean and Standard Deviation. They are shown below:
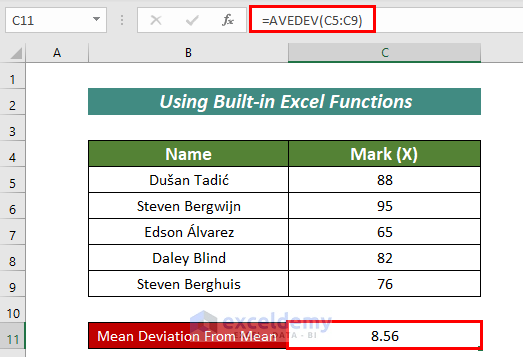
1. Mean Deviation From Mean
We can calculate the Mean Deviation From the Mean with the AVEDEV function.
The formula is:
=AVEDEV(C5:C9)
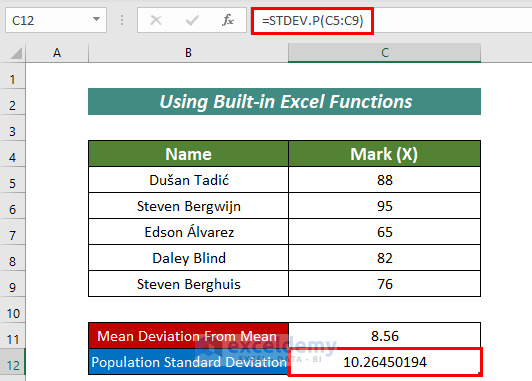
2. Population Standard Deviation
With the STDEV.P function, we can calculate the Population Standard Deviation.
The formula is:
=STDEV.P(C5:C9)3. Sample Standard Deviation
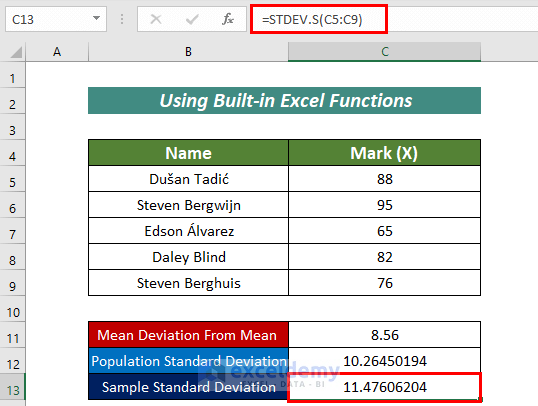
With the STDEV.S function, we can calculate Sample Standard Deviation.
The formula is:
=STDEV.S(C5:C9)Thus, with the help of the built-in functions, we can simply calculate Mean and Standard Deviation in Excel.
Calculating Different Types of Standard Deviations in Excel
There are a few functions that can be used to calculate Standard deviations. They are:
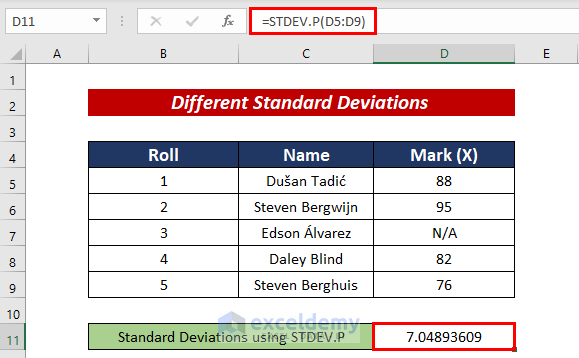
1. STDEV.P Function
We can calculate Standard deviations with the STDEV.P function. In order to calculate the entire population, the STDEV.P Function is used.
For this, we need to follow the following formula:
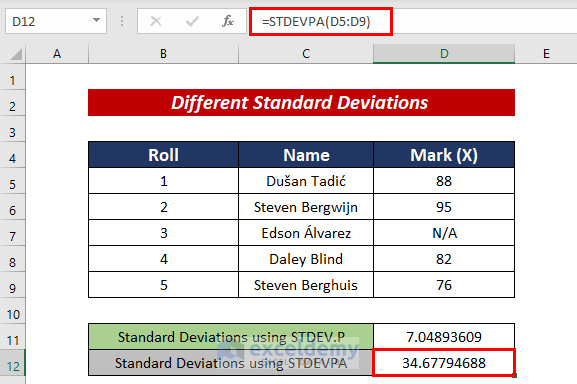
=STDEV.P(D5:D9)2. STDEVPA Function
We can also calculate Standard deviations with the STDEVPA function.
For this, we need to follow the following formula:
=STDEVPA(D5:D9)Read More: How to Calculate Standard Deviation of y Intercept in Excel
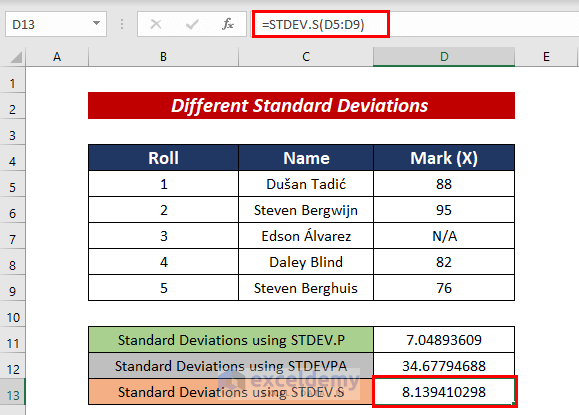
3. STDEV.S Function
With the help of the STDEV.S function, we can calculate Standard deviations too. This is used for the sample dataset, not the entire population.
For this, we need to follow the following formula:
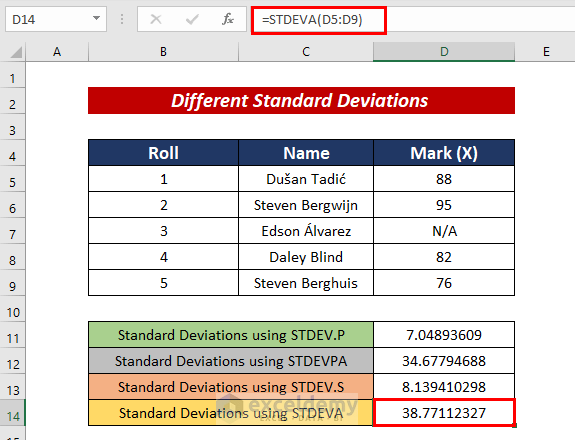
=STDEV.S(D5:D9)4. STDEVA Function
Using the STDEVA function, we can calculate Standard deviations too. It takes into account logical values too.
For this, we need to follow the following formula:
=STDEVA(D5:D9)Practice Section
For more expertise, you can practice here.
Download Practice Workbook
Conclusion
In this article, I have tried to explain how to calculate the mean and standard deviation in Excel. It will be a matter of great pleasure for me if this article could help any Excel user even a little. For any further queries, comment below. You can visit our site for more articles about using Excel.
Related Articles
- How to Calculate Standard Deviation of a Frequency Distribution in Excel
- Calculate Percentile from Mean and Standard Deviation in Excel
- How to Calculate Uncertainty in Excel
<< Go Back to Standard Deviation Formula in Excel | Excel for Statistics | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!