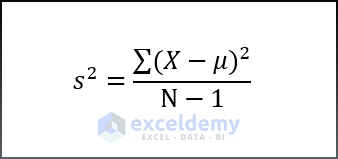Both Variance and Standard Deviation are popular terms in statistical analysis. Do you know Excel provides multiple opportunities to calculate those in your Excel workbook, even without knowing any mathematical jargon? This article focuses on diverse methods of how to calculate Variance and Standard Deviation in Excel.
Basics of Variance and Standard Deviation
Before delving into today’s discussion, let’s have a quick overview of Variance and Standard Deviation. Instead of utilizing more general mathematical procedures like grouping numbers into quartiles, statisticians employ Variance to examine how distinct numerical values relate to one another within a data collection. In addition, Variance has the benefit of treating all values that have deviated from the mean equally, regardless of their direction. On the other hand, Standard Deviation provides a brief overview of how the values are distributed over a given dataset.
There are two types of Variance statisticians usually take into account, and the corresponding formula can be described as follows,
- Population variance
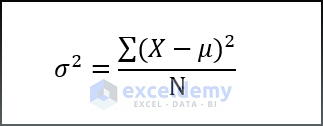
- Sample variance
Where,
- X= Value of each data point,
- μ= Mean value,
- N= Sample Size.
On the contrary, the formula of Standard Deviation is nearly identical to that of the Variance. All you need to do is square root each Variance to get the corresponding Standard Deviation.
Diverse Methods to Calculate Variance and Standard Deviation in Excel
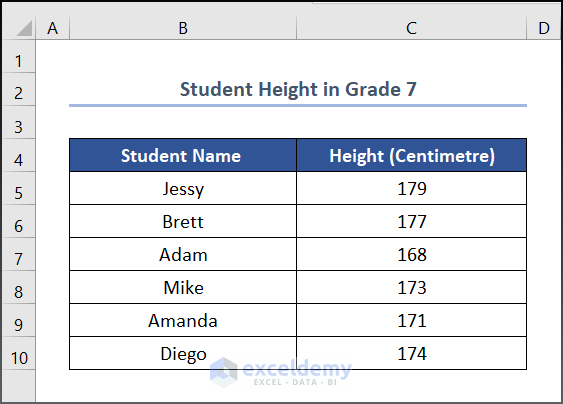
Let’s assume we have a dataset, namely “Student Height in Grade 7”. You can use any dataset suitable for you.
Here, we have used the Microsoft Excel 365 version; you may use any other version according to your convenience.
1. Calculating Variance
To calculate the Variance of our given dataset, we will use three possible methods, such as the arithmetic formula, VAR, and VARA functions. We will find both Sample and Population Variance at the same time. So let’s take a deep dive.
1.1 Using Arithmetic Formula
📌 Steps:
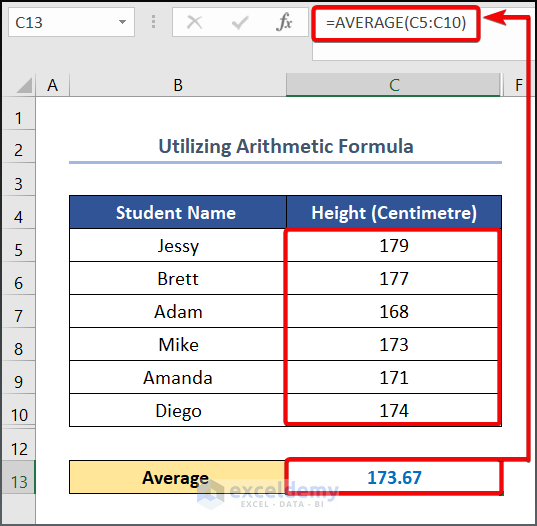
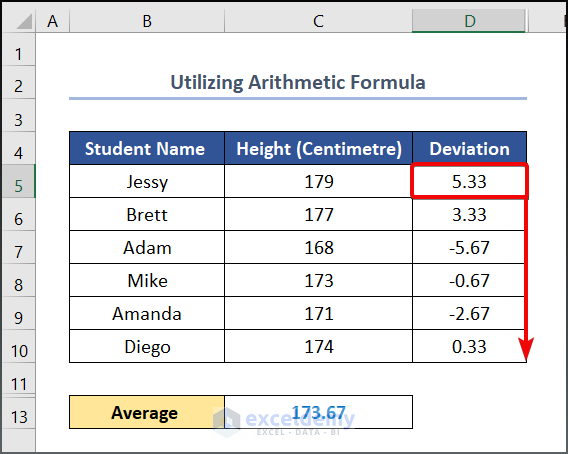
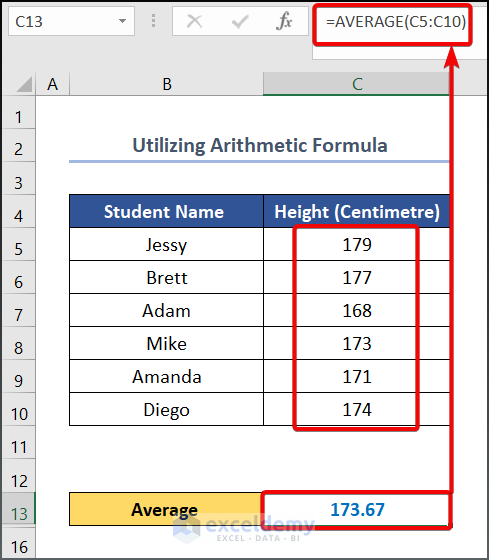
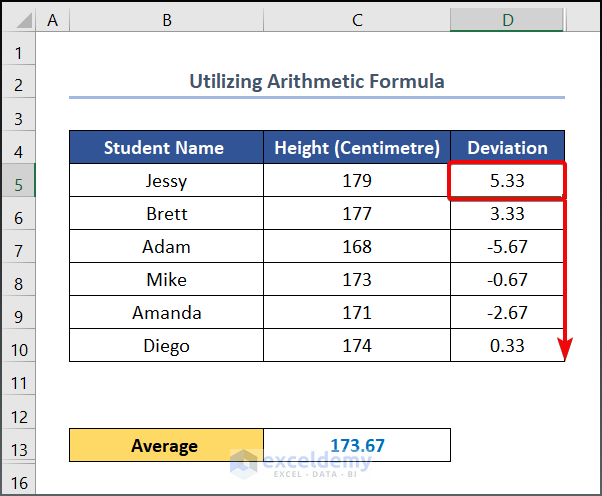
- To begin with this method, enter the following formula in cell C13.
=AVERAGE(C5:C10)- Press on the ENTER button to see the output.
Alt Text: Using Arithmetic Formula to Calculate Variance in Excel
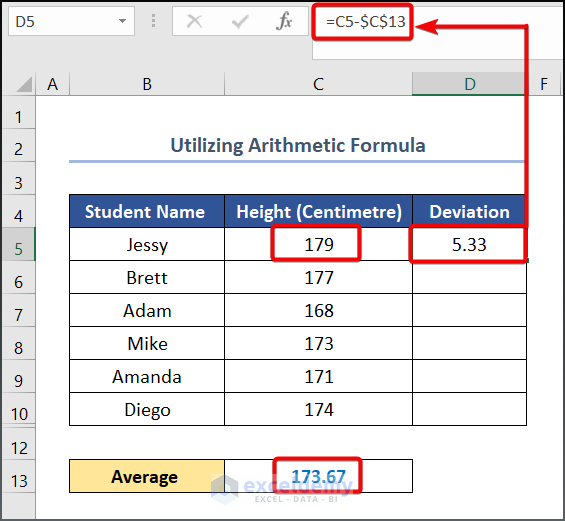
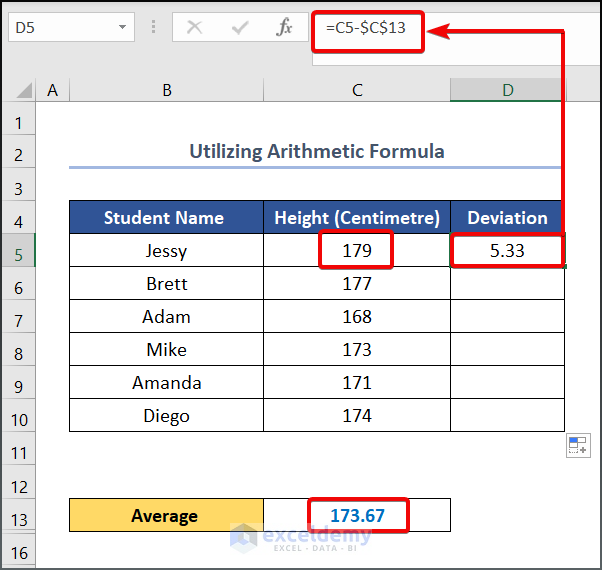
- Write the following formula in cell D5.
=C5-$C$13
Here, C5 and C13 cells refer to the student’s Height and Average values respectively.
- Drag the Fill Handle tool to get the other values.
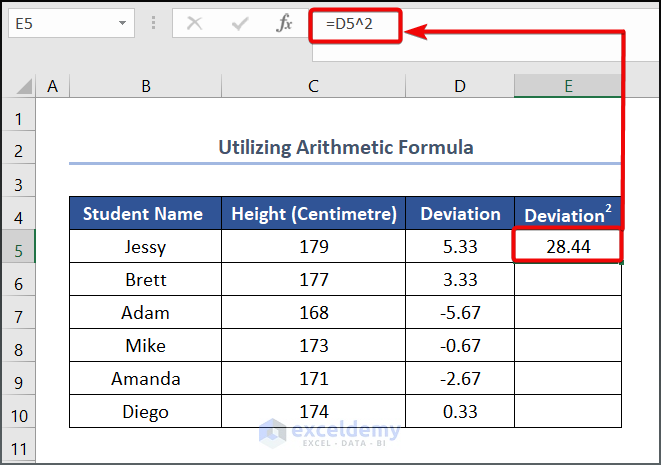
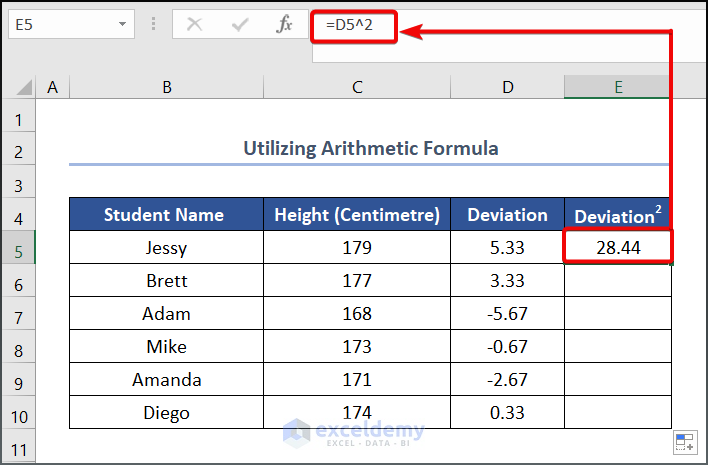
- To get the squared value of Deviation, write the following formula in cell E5.
=D5^2
Here, D5 refers to the Deviation.
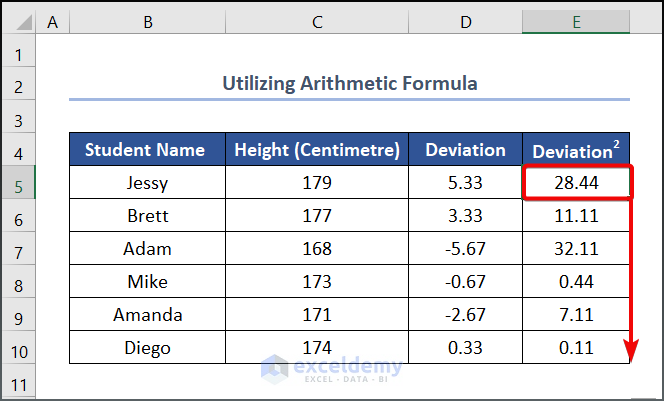
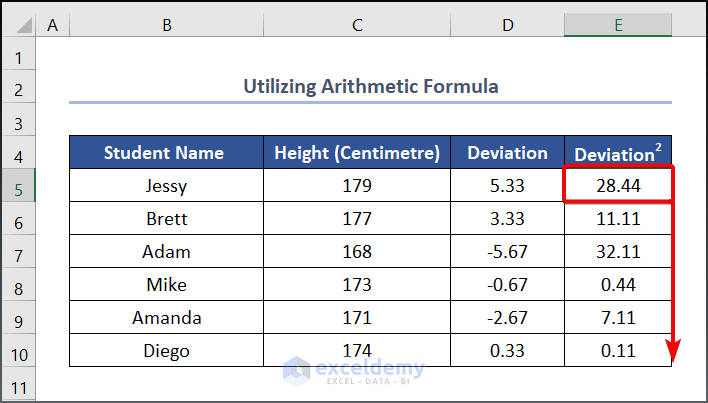
- To get the other value, drag the Fill Handle tool from E5 to E10.
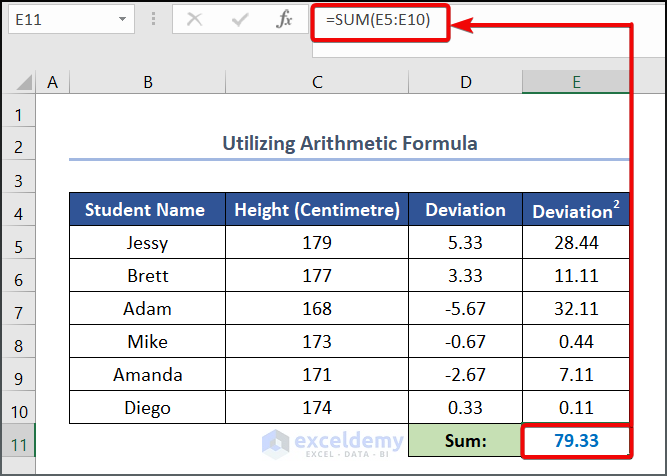
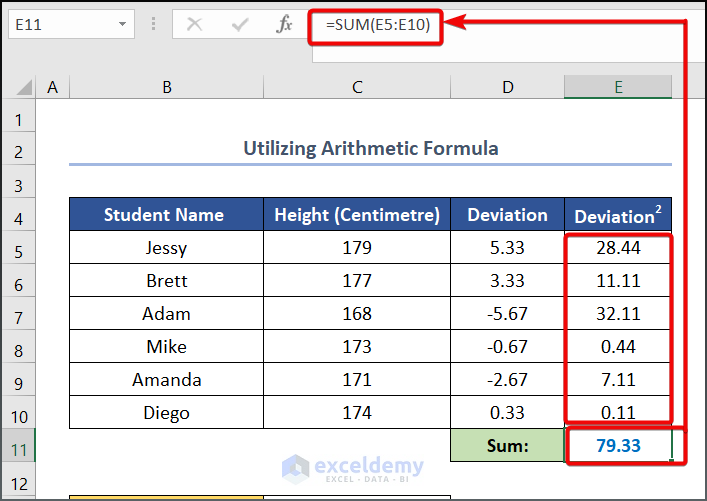
- Write the following formula in cell E11 to calculate the sum of the squared deviation value.
=SUM(E5:E10)
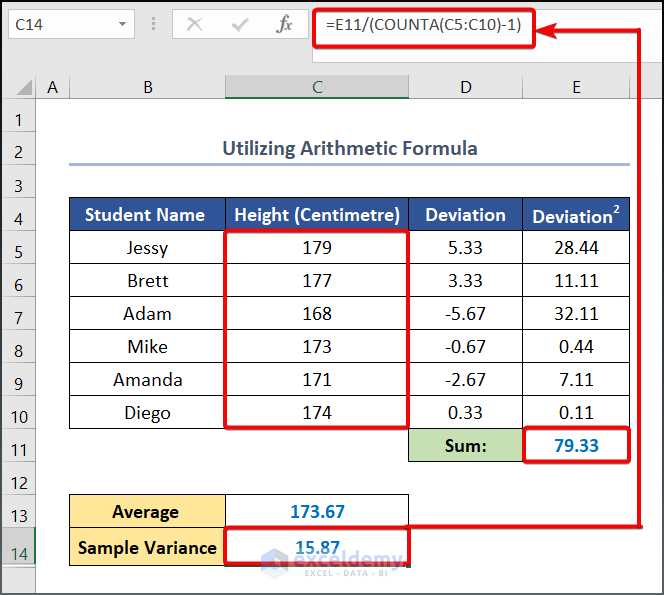
- Now, to calculate the Sample Variance, enter the following formula in cell C14.
=E11/(COUNTA(C5:C10)-1)
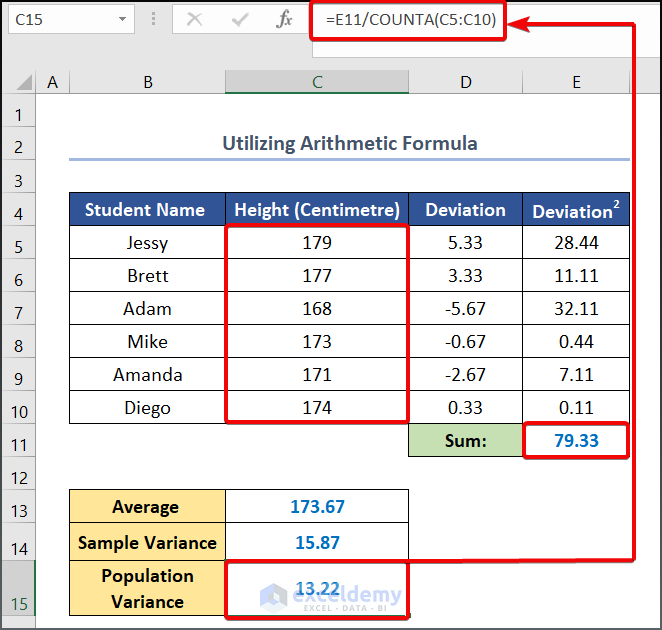
- Similarly, write the following formula in cell C15 to calculate the Population Variance.
=E11/COUNTA(C5:C10)
1.2 Using VAR Function
Another way to accomplish the previous task is to incorporate the VAR function into the formula bar. To get hands-on experience with how to do this, follow the steps that we are going to describe below.
📌 Steps:
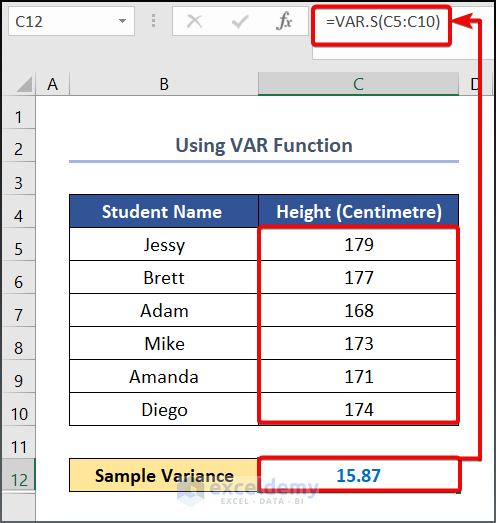
- Write the following formula in cell C12.
=VAR.S(C5:C10)
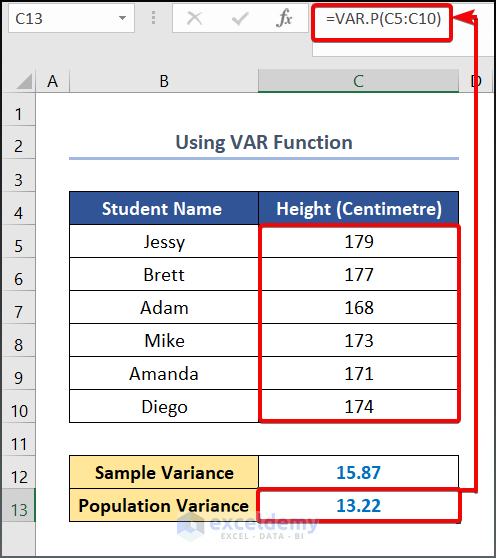
- Similarly, enter the following formula in cell C13, to calculate Population Variance.
=VAR.P(C5:C10)
1.3 Applying VARA Function
Both VARA and VAR functions are the same in terms of the output they return. Follow the steps given below to get an idea about it.
📌 Steps:
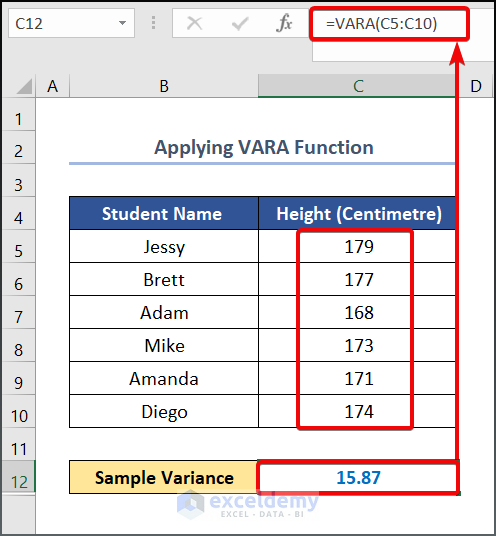
- Write the following formula in cell C12.
=VARA(C5:C10)
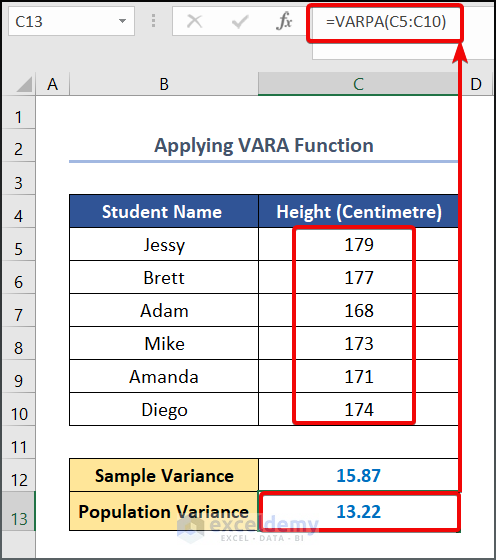
- Enter the following formula in cell C13.
=VARPA(C5:C10)
Read More: How to Calculate Quartile Deviation in Excel
2. Calculating Standard Deviation
As we did previously, we will now calculate the Standard Deviation of our given dataset in a similar fashion. However, other than the arithmetic formula that we have given in our introduction, we will use the STDEV.P, STDEV.S, STDEVA, and STDEVPA functions to accomplish the task.
2.1 Utilizing Arithmetic Formula
📌 Steps:
- First of all, enter the following formula in cell C13.
=AVERAGE(C5:C10)
- Press the ENTER button to see the output.
- Write the following formula in cell D5.
=C5-$C$13
- Drag the Fill Handle tool to get the other values.
- Write the following formula in cell E5.
=D5^2
- To get the other value, drag the Fill Handle tool.
- Write the following formula in cell E11 to calculate the sum of the squared deviation value.
=SUM(E5:E10)
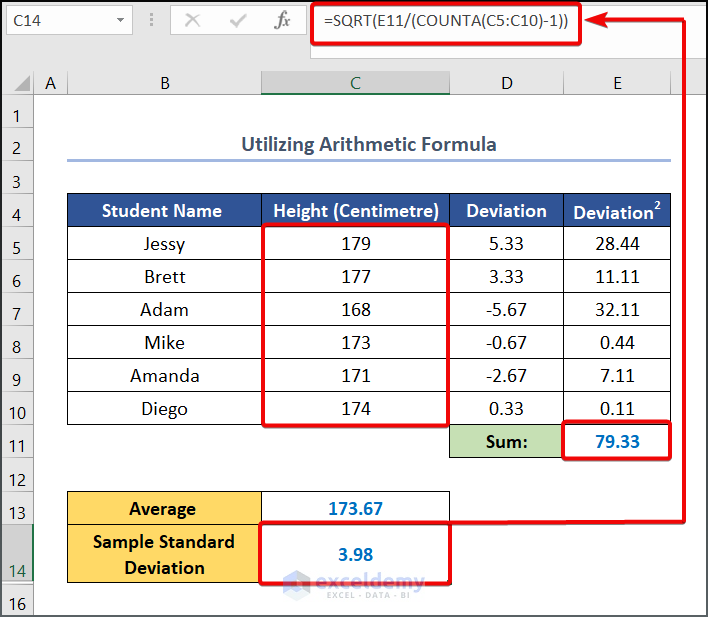
- Now, to calculate the Sample Standard Deviation, enter the following formula in cell C14.
=SQRT(E11/(COUNTA(C5:C10)-1))
Formula Breakdown
- COUNTA(C5:C10) → Here the COUNTA function counts the number of cells in a range that are not empty. Here, the C5:C10 is the value1 argument that refers to the Height.
- Output → 6
- SQRT(E11/(COUNTA(C5:C10)-1)) →The given SQRT function divides the E11 cell value to COUNTA(C5:C10)-1 and returns the square root output to cell C14.
- Output → 3.98
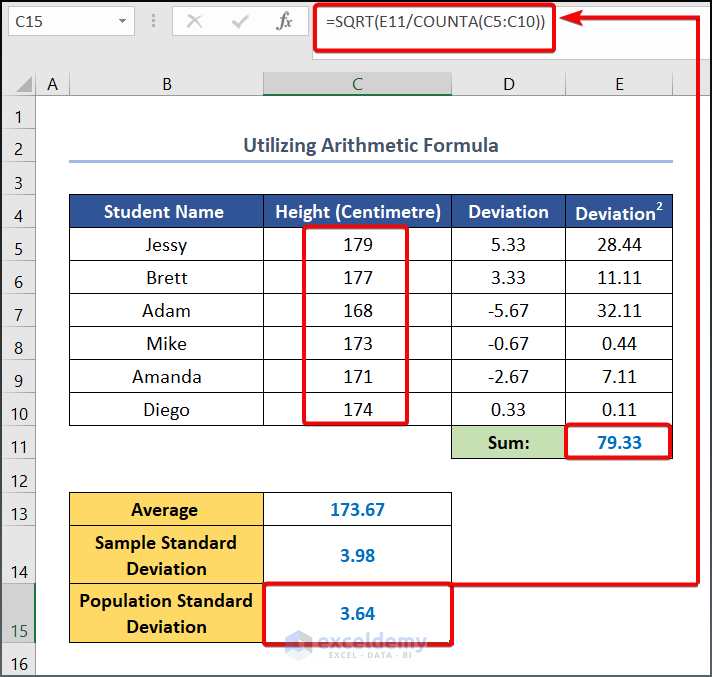
- Similarly, write the following formula in cell C15 to calculate the Population Standard Deviation.
=E11/COUNTA(C5:C10)
2.2 Applying STDEV Function
Excel is always open to providing various functions to minimize your effort. Like, you can employ the STDEV function if you want to avoid the arithmetic formula.
📌 Steps:
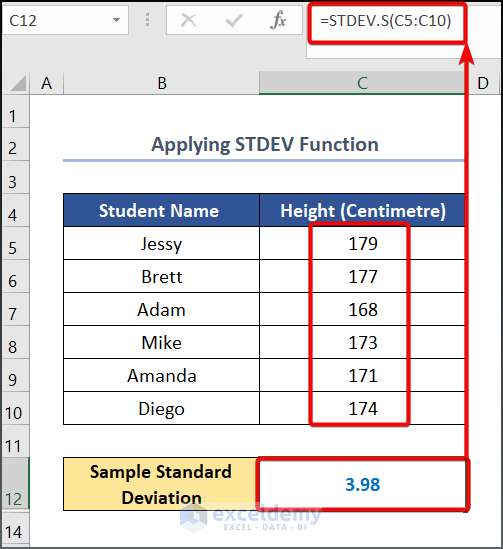
- Write the following formula in cell C12.
=STDEV.S(C5:C10)
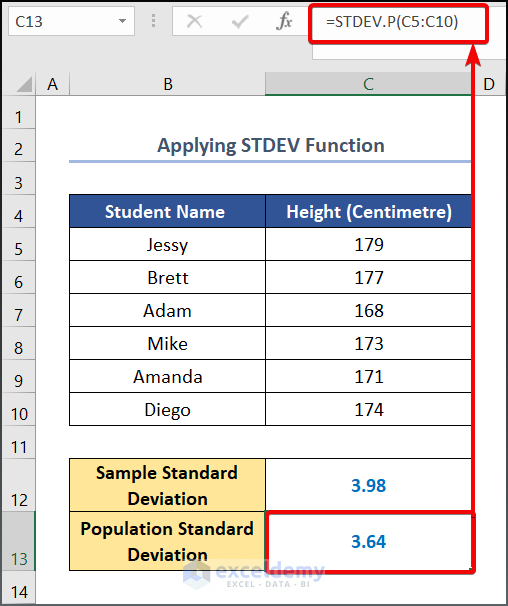
- Similarly, type the following formula to get the Population Standard Deviation.
=STDEV.P(C5:C10)
2.3 Employing STDEVPA Function
So far, so good. The last resort we are going to employ is the STDEVPA function to get the Standard Deviation.
📌 Steps:
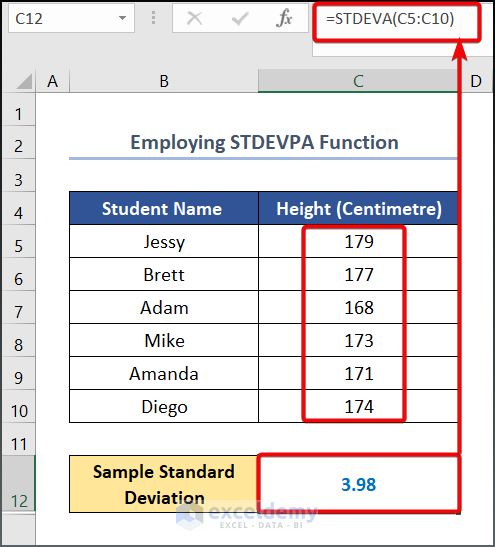
- First, input the following formula in cell C12.
=STDEVA(C5:C10)
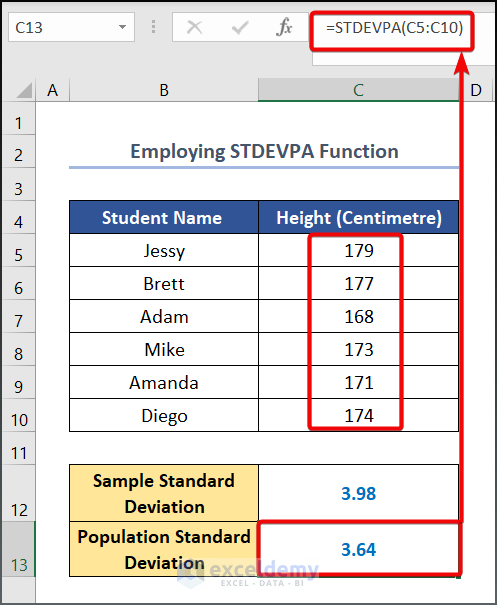
- Next, copy and paste the following formula in cell C13.
=STDEVPA(C5:C10)
Practice Section
We have provided a Practice section on the right side of each sheet, so you can practice yourself. Please make sure to do it yourself.
Download Practice Workbook
You can download and practice the dataset that we have used to prepare this article.
Conclusion
In this article, we have discussed how to calculate Variance and Standard Deviation in Excel. As you have already understood, there are plenty of ways to accomplish this task. Further, if you have any queries, feel free to comment below, and we will get back to you soon.
