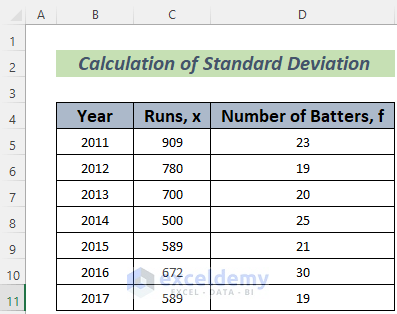
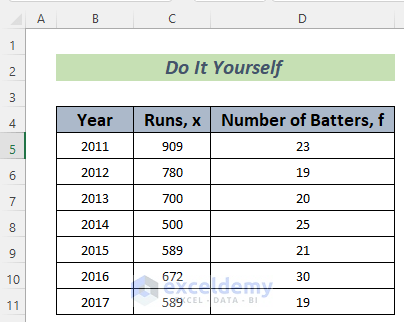
How to Calculate Standard Deviation of a Frequency Distribution in Excel

We have the batting statistics across Years. We’ll determine the deviation between years.

What Is Standard Deviation?

The term Standard Deviation is a measurement of the scattering of a set of values from their mean. If the Standard Deviation of a set of values is high, we can say that the data highly deviates from its mean or average, which implies that the values are independent. If the Standard Deviation is low, we can say that the data stays close to its mean and there is a greater possibility of them being related to each other. The mathematical formula for Standard Deviation is given below.

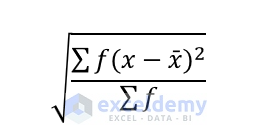
f = Frequency of the Data

x = Each Value of the Data

x̄ = Mean of the Data

How to Calculate the Standard Deviation of a Frequency Distribution in Excel: 2 Ways

Method 1 – Using a Mathematical Formula to Calculate the Standard Deviation of a Frequency Distribution

We’ll determine the Standard Deviation of the Runs that these batters scored using the mathematical formula. The Frequency of this data is the number of players that scored a certain amount of runs each year.

Steps:

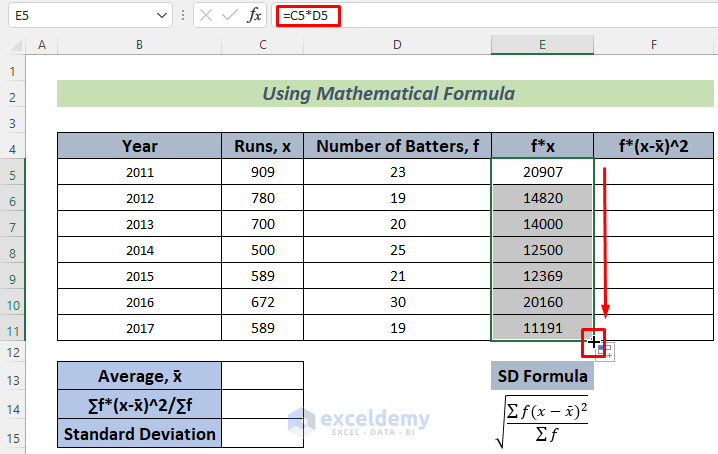
Use the following formula in cell E5.

=C5*D5

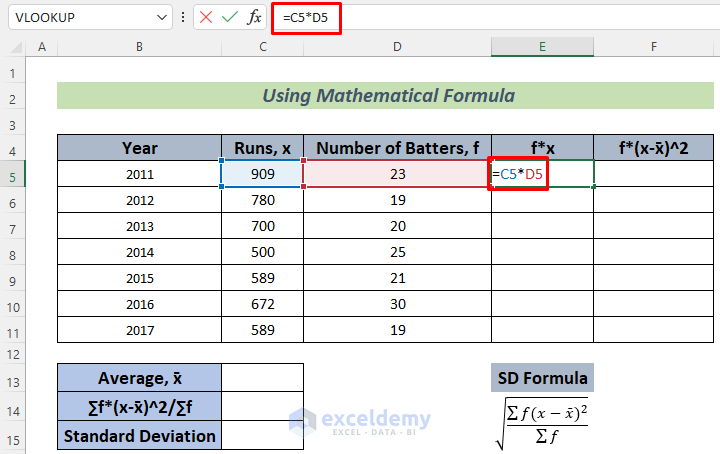
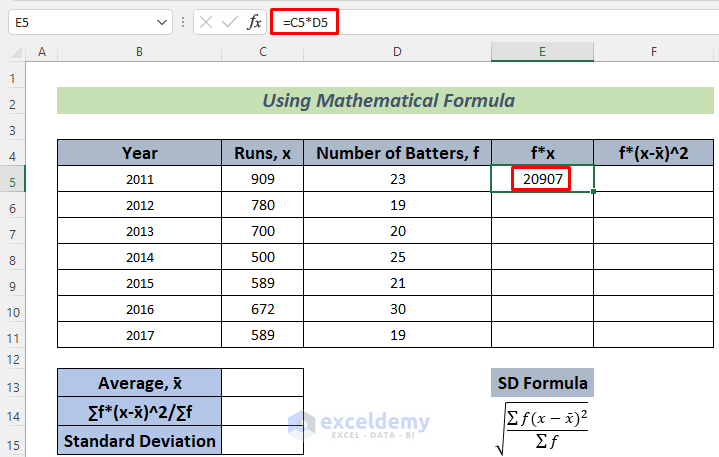
This formula will store the total runs scored by the batters in 2011.

Hit the Enter button and you will see the total runs that these players scored together in 2011.

Use the Fill Handle to AutoFill down.

Use the formula below in cell C13 and press Enter.

=SUM(E5:E11)/SUM(D5:D11)

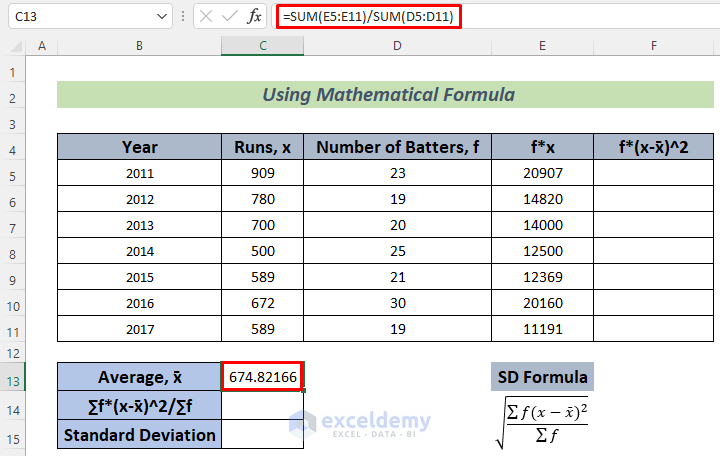
The formula will return the Average runs per year of a Batter with the help of the SUM function.

Use the following formula in cell F5, press Enter, and use Fill Handle to AutoFill.

=D5*(C5-$C$13)^2

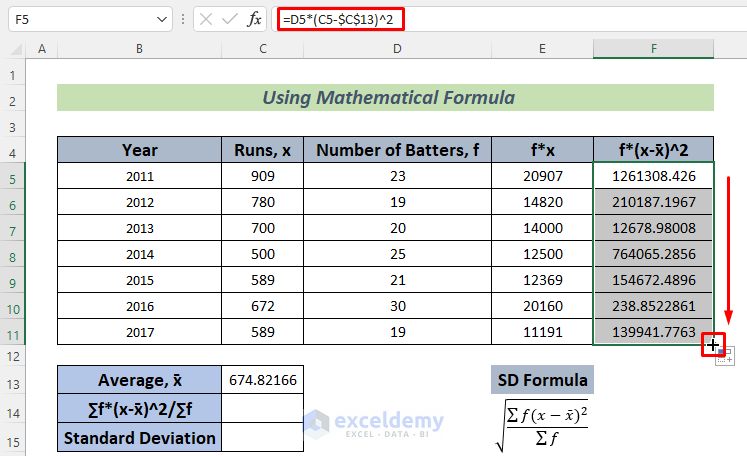
This formula will store the f*(x-x̄)^2 value for each year.

Use the following formula in cell C14 and press Enter.

=SUM(F5:F11)/SUM(D5:D11)

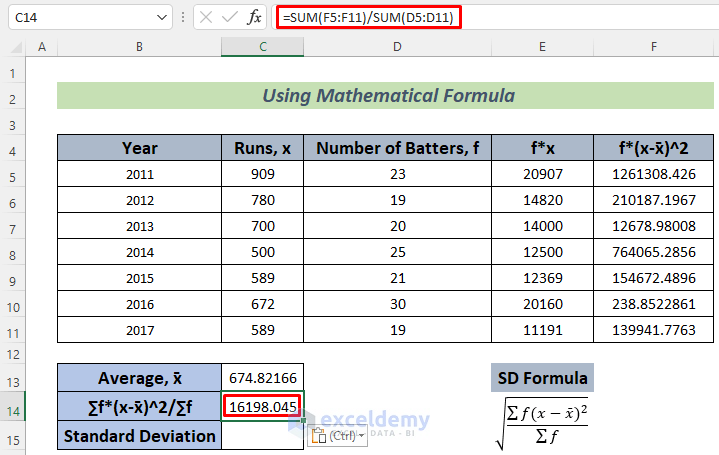
This will calculate the Variance of this data.

Use the following formula in cell C15 and press Enter.

=SQRT(C14)

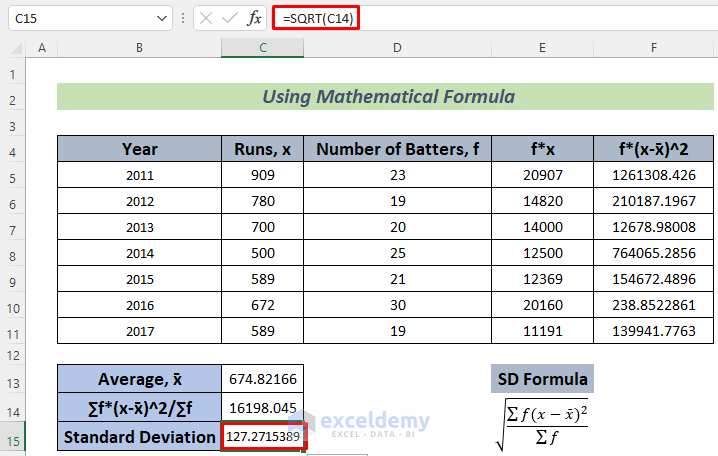
As Standard Deviation is the square root of Variance, we use the SQRT Function to determine the square root of the value in C14.

Method 2 – Applying the SUMPRODUCT Function to Calculate a Standard Deviation of a Frequency Distribution

Steps:

Use the following formula in cell C13.

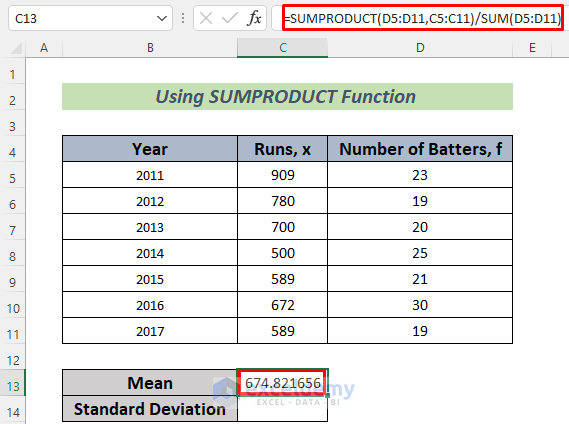
=SUMPRODUCT(D5:D11,C5:C11)/SUM(D5:D11)

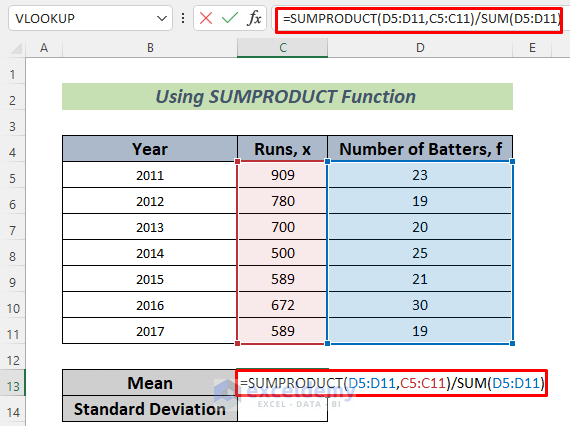
The SUMPRODUCT function will return the total runs over the 7 years. We want the average runs scored by each batter in a year, so we divided it by the total number of batters. We used the Excel SUM Function to input the number of total batters.

Press Enter to see the result.

Use the following formula in cell C14.

=SQRT(SUMPRODUCT((C5:C11-C13)^2,D5:D11)/SUM(D5:D11))

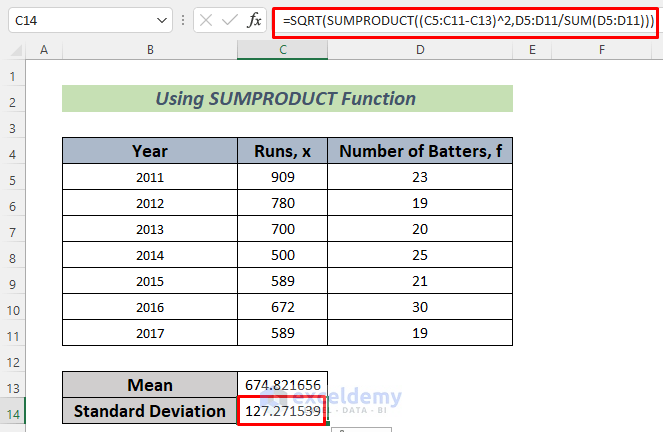
We used the SQRT Function to determine the square root of Variance and hence calculate the Standard Deviation

Formula Breakdown

SUM(D5:D11) —-> returns the total number of batters
- Output: 157
(C5:C11-C13)^2 —-> returns a range of values which are squares of the difference between the data (runs) and mean.
SUMPRODUCT((C5:C11-C13)^2,D5:D11) —-> results in the summation of the products between the range (C5:C11-C13)^2 and D5:D11
- Output: 2543093.00636943
SUMPRODUCT((C5:C11-C13)^2,D5:D11)/SUM(D5:D11) —-> becomes
2543093.00636943/157
- Output: 16198.0446265569
SQRT(SUMPRODUCT((C5:C11-C13)^2,D5:D11)/SUM(D5:D11)) —-> turns into
SQRT(16198.0446265569)
- Output: 127.271538949432