We often need to measure standard deviation in statistical datasets. We can calculate the standard deviation of the y intercept in Excel. In this article, we have discussed two easy steps for how to calculate the standard deviation of the y intercept in Excel.
What Is the Standard Deviation of y Intercept?
The concept of standard deviation is typically used to describe the spread or variability of a set of data points around a central value or average. It is a statistical calculation that gives an idea of how spread out the data is from the average value. In a linear regression model, the y-intercept represents the predicted value of the dependent variable (y) when the independent variable (x) is equal to zero. We can calculate the standard deviation of the y-intercept by using different functions in Excel.
How to Calculate Standard Deviation of y Intercept in Excel: With Easy Steps
There are two steps to calculating the standard deviation of the y-intercept. At first, we will calculate y intercepts from the dataset. Then, we will look for the standard deviation of the y-intercepts.
Here in the dataset, we have the Sales Quantity (independent variable or x value) and the Profit (dependent variable or y value) of a company for the entire year. We will divide the annual year into three quarters (Quarter 1, Quarter 2, and Quarter 3). From these three quarters, we will find three y-intercepts, respectively. Then, we will measure the standard deviation of the y-intercepts.
Step 1: Find y Intercept to Calculate Standard Deviation in Excel
In the first step, we need to find the y-intercept of the given dataset. We can use various functions to find the y-intercept in Excel.
We can find the y-intercept by simply using the INTERCEPT function in Excel. Follow the steps below:
- Select a cell where you want to see the y-intercept. Here, we are selecting cell C19 to see the y-intercept for the first quarter. Enter the following formula into the cell:
=INTERCEPT(D5:D8,C5:C8)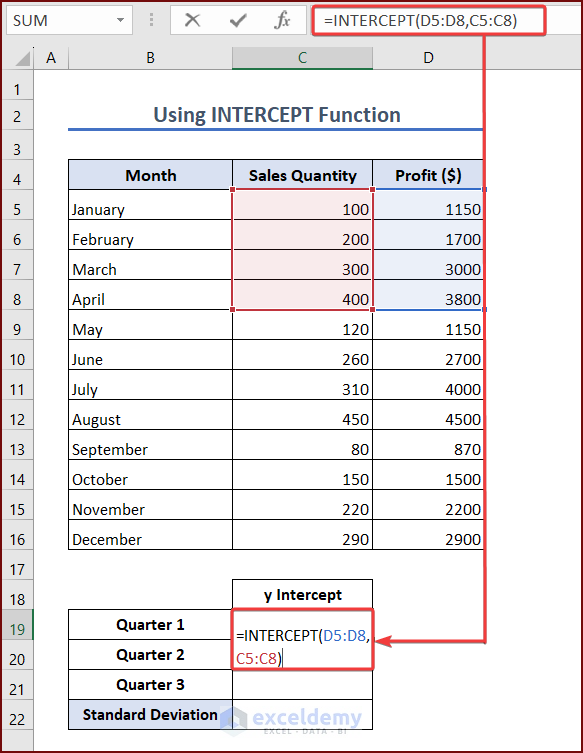
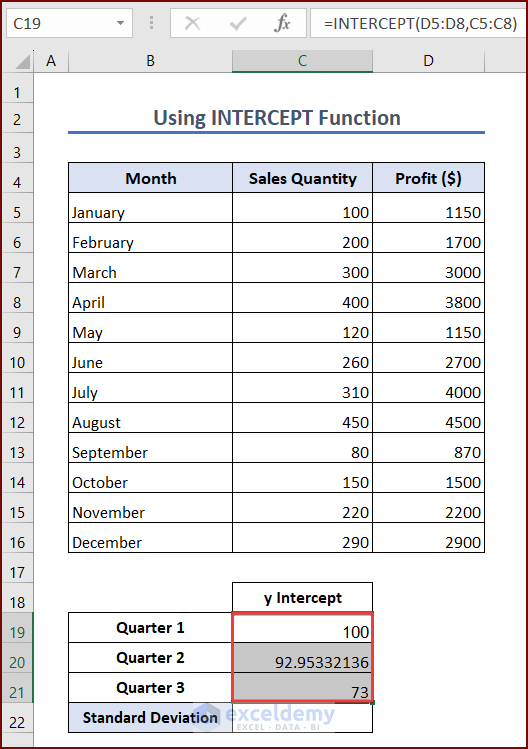
- Press Enter and you will see the y-intercept for the first quarter in cell C19. Now enter the following formulae in cells C20 and C21 to get the y-intercepts for the second and third quarters respectively:
=INTERCEPT(D9:D12,C9:C12)=INTERCEPT(D13:D16,C13:C16)
2. Combine AVERAGE and SLOPE Functions
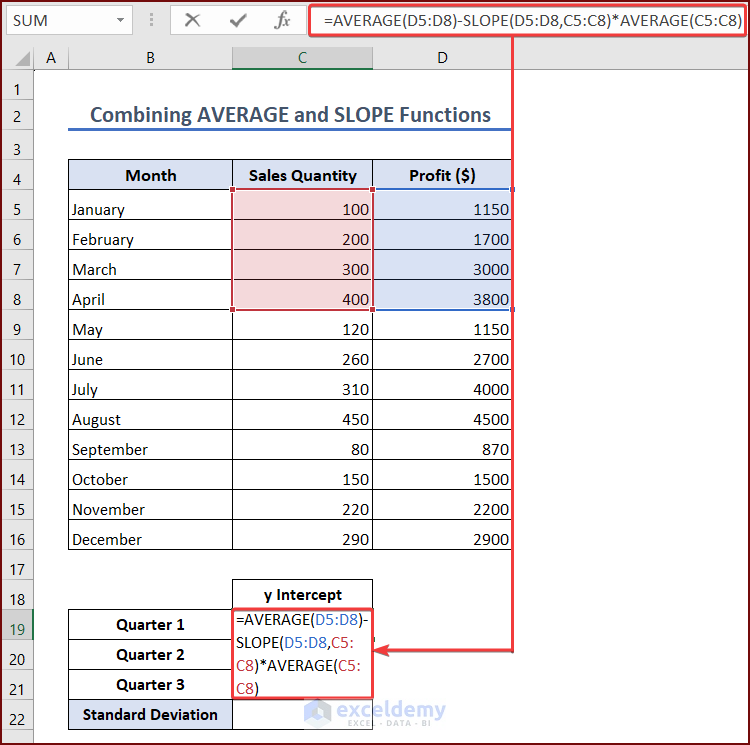
We can combine the AVERAGE and SLOPE functions to calculate the y intercept. Just follow these steps:
- Select cell C19 to see the y-intercept for the first quarter. Enter the following formula into the cell:
=AVERAGE(D5:D8)-SLOPE(D5:D8,C5:C8)*AVERAGE(C5:C8)
Formula Breakdown
- AVERAGE(D5:D8): In the first portion we have used the AVERAGE This function will take the values of cells D5:D8 and will calculate the arithmetic mean or average of these values accordingly.
- SLOPE(D5:D8,C5:C8): In this portion, the SLOPE function takes two inputs. The first input is the range of cells that represent y values and the second input is the range of cells that represent x values. This function returns the slope of the input data points.
- AVERAGE(D5:D8)-SLOPE(D5:D8,C5:C8)*AVERAGE(C5:C8): This whole formula calculates the y-intercept of the input data points.
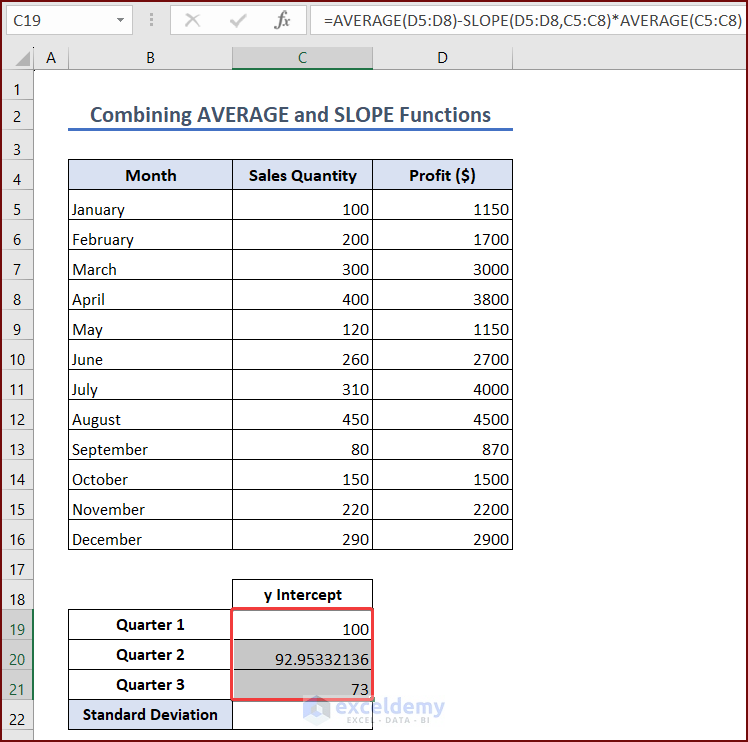
- Press Enter and you will see the y-intercept for the first quarter in cell C19. Now enter the following formulae in cells C20 and C21 to get the y-intercepts for the second and third quarters respectively:
=AVERAGE(D9:D12)-SLOPE(D9:D12,C9:C12)*AVERAGE(C9:C12)=AVERAGE(D13:D16)-SLOPE(D13:D16,C13:C16)*AVERAGE(C13:C16)
3. Use the LINEST Function
We can use the LINEST function to find the value of the y-intercept in Excel. The LINEST is an array formula. So, it returns multiple outputs, and each output signifies different values. Just follow the steps below:
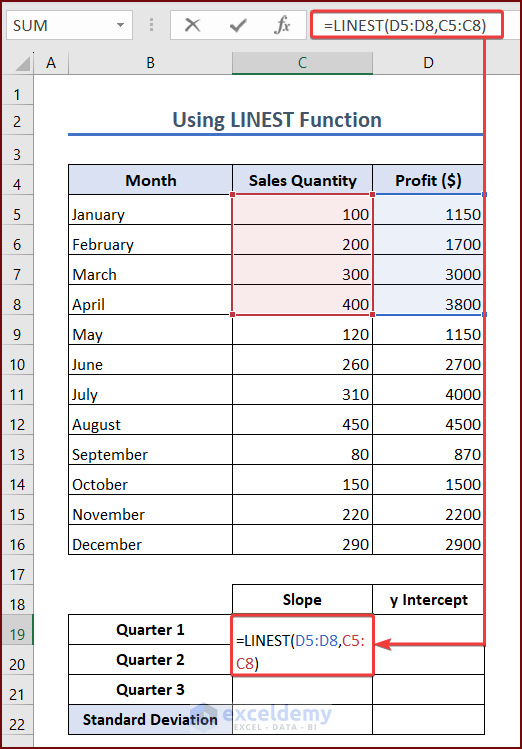
- Select cell C19 and enter the formula into the cell:
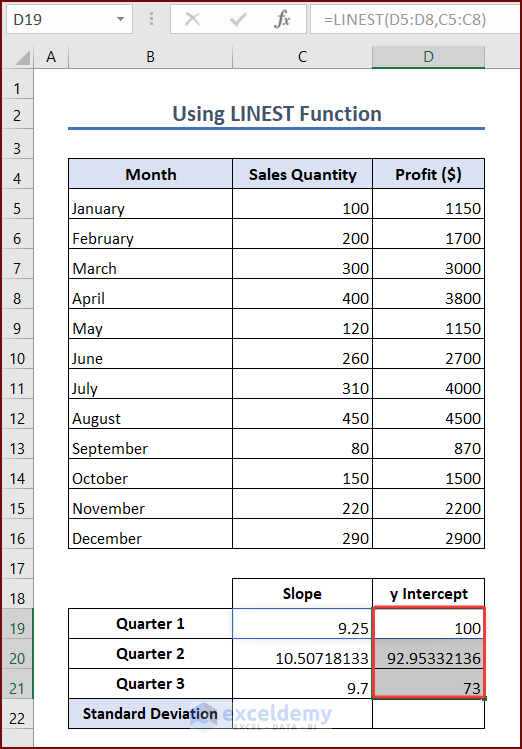
=LINEST(D5:D8,C5:C8)
- Press Enter, and the LINEST function will return two values in two consecutive cells. The first one is the slope and the second one is the y-intercept. So, the y-intercept for the first quarter will be in cell D19.
- Now enter the following formulae in cells C20 and C21. You will get the y-intercepts for the second and third quarters in cells D20 and D21 respectively:
=LINEST(D9:D12,C9:C12)=LINEST(D13:D16,C13:C16)
Read More: How to Calculate Population Standard Deviation in Excel
Step 2: Using STDEV and STDEV.S Functions to Calculate Standard Deviation of y Intercept in Excel
We can use multiple functions to calculate the standard deviation in Excel. The STDEV or STDEV.S functions are used to calculate the standard deviation of a sample dataset. We can also use the STDEV.P function to calculate the standard deviation of an entire population. As we have a small sample data set, we can use the STDEV or STDEV.S function to calculate the standard deviation of the y-intercept.
1. Use STDEV Function
We can use the STDEV function to calculate the standard deviation of the y-intercept in Excel. This formula is compatible with Excel 2007 and earlier. Follow the steps below:
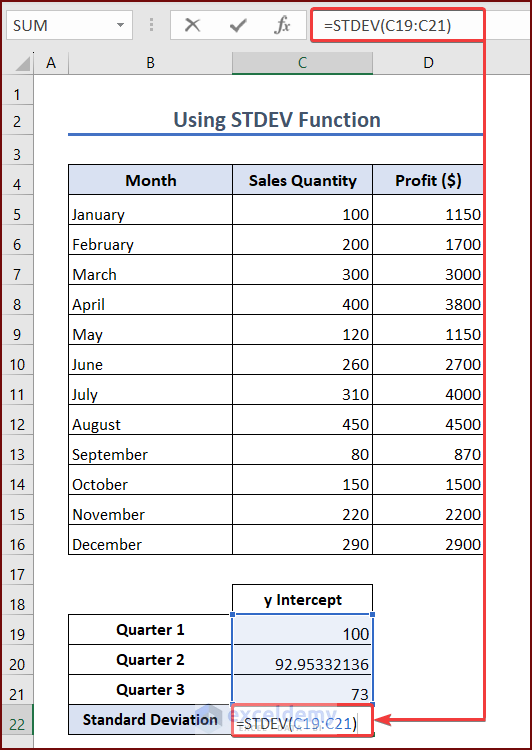
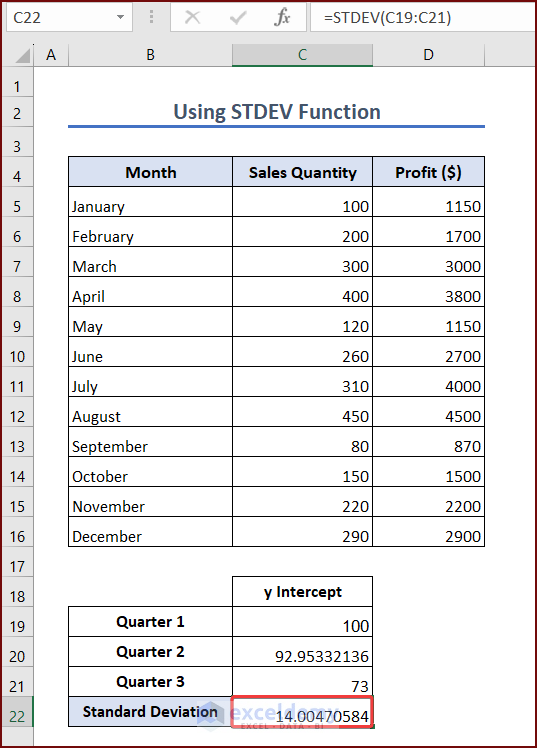
- Select a cell where you want to see the standard deviation of the y-intercept. We are selecting cell C22. Enter the formula into the cell:
=STDEV(C19:C21)
- Press Enter, and you will see the standard deviation of the y-intercept in cell C22.
2. Use STDEV.S Function
We can use the STDEV.S function as well to calculate the standard deviation of the y-intercept. Just follow these steps:
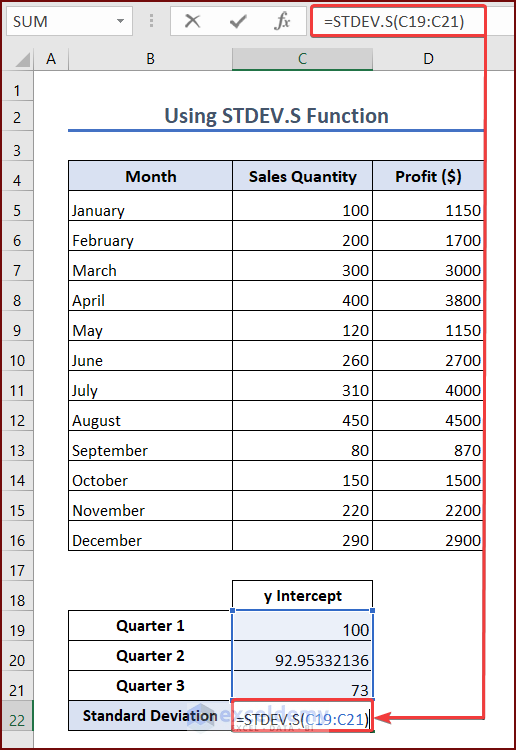
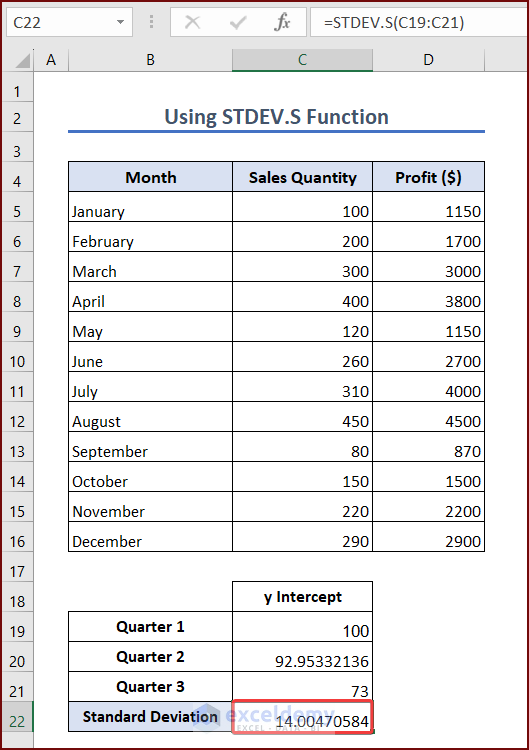
- Select a cell where you want to see the standard deviation of the y-intercept. We are selecting cell C22. Enter the formula into the cell:
=STDEV.S(C19:C21)
- Press Enter, and you will see the standard deviation of the y-intercept in cell C22.
Read More: How to Calculate Standard Deviation with IF Conditions in Excel
Error in Intercept in Excel
The standard error represents how much the data may deviate from a standard or mean value. We can find the standard error of the y-intercept by using the LINEST function. The LINEST function returns an array of outputs, and you will find a standard error there. You need to follow the steps below:
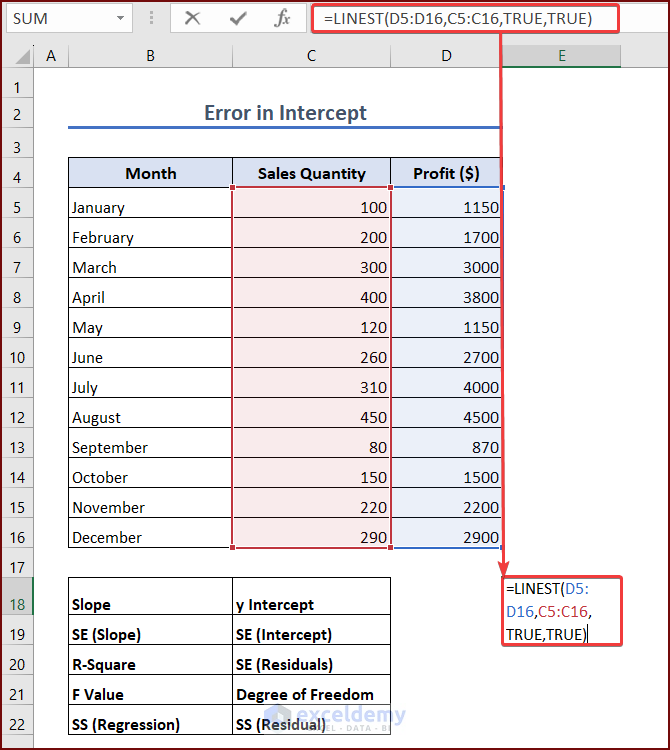
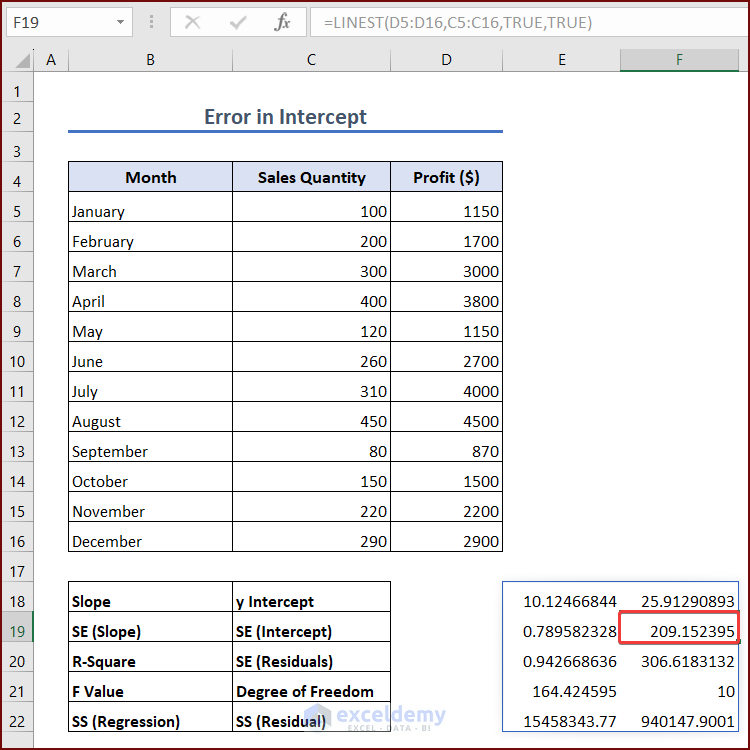
- Select a cell to enter the formula. We are selecting cell E18:
=LINEST(D5:D16,C5:C16,TRUE,TRUE)
- Press Enter and you will see an array of outputs. Cells B18:C22 represent the output values of cells E18: F22. It is visible that the standard error of y-intercept is the value in cell F19.
Things to Remember
There are a few things to remember while calculating the standard deviation of the y-intercept in Excel:
- Use the correct formula. If the data set is a sample dataset, use S and if it is a population dataset use the STDEV.P function.
- The LINEST function returns multiple outputs. Carefully choose the value you want from the array of outputs.
Frequently Asked Questions
1. What does a high or low standard deviation mean?
A high standard deviation indicates that the data points are spread out widely from the mean, whereas a low standard deviation means that the data points are clustered closely around the mean.
2. Can the standard deviation be negative?
No, the standard deviation cannot be negative. It is always either a positive number or zero.
3. Can the standard deviation be greater than the mean?
Yes, the standard deviation can be greater than the mean if the data points are spread out widely from the mean.
Download Practice Workbook
You can download the practice workbook while going through this article.
Conclusion
In this article, we have demonstrated two easy steps on how to calculate the standard deviation of y intercept in Excel using different functions. This article will allow users to use Excel more efficiently and effectively. Â If you have any questions regarding this essay, feel free to let us know in the comments.
Related Articles
- How to Calculate Standard Deviation of a Frequency Distribution in Excel
- Calculate Percentile from Mean and Standard Deviation in Excel
- How to Calculate Uncertainty in Excel
Hi,
I have a question. I see that you used the “standard error” directly as “standard deviation of the y intercept”. I think they are different terms, so strictly speaking, are they supposed to be different values?
Thanks.
Hello Z L
Thank you very much for your response. We have modified this article and introduced some new statistical concepts and functions. Would you please go through it again?
If you have any more questions, let us know in the comment section.
Thanks
Md. Abu Sina Ibne Albaruni
Team ExcelDemy