The LINEST function is a built-in function in Excel that is categorized as a Statistical Function. It is one of those essential functions. In this tutorial, you will learn every detail of the LINEST function in Excel. This tutorial will be on point with suitable examples and proper illustrations.
The Excel LINEST function returns statistics for a reasonably fit linear line through supplied x and y values. The values produced by LINEST contain slope, intercept, standard error values, and more. To discover the best fit of a line to the data, LINEST uses the “least squares” procedure. The equation for the line is:
y = mx + b (for single range of x)
y = m1x1 + m2x2 + … + b (multiple ranges of x)
It returns an array of values. So you have to enter this as an array formula.
The above screenshot is an overview of the article. It represents a simplified application of the LINEST function in Excel. You’ll learn more about the dataset as well as the methods and procedures under different criteria in the following sections of this article.
Introduction to LINEST Function
⏺ Function Objective
Find the least-squares method to compute the statistics for a straight line and return an array describing that line.
⏺ Syntax
⏺ Arguments Explanations
| Argument | Required/Optional | Explanation |
|---|---|---|
| known_y’s | Required | The set of y-values that we already know in the relationship y = mx + b.
|
| [known_x’s] | Optional | A set of x-values that we may already know in the relationship y = mx + b.
|
| [const] | Optional | A logical value specifying whether to force the constant b to equal 0.
|
| [stats] | Optional | A logical value defining whether to return additional regression statistics.
|
The following table will describe additional regression statistics:
| Statistics | Description |
|---|---|
| se1,se2,…,sen | The standard error values for the coefficients m1,m2,…,mn. |
| seb | The standard error value for the constant b (seb = #N/A when const is FALSE). |
| r2 | The coefficient of determination. Compares estimated and actual y-values, and ranges in value from 0 to 1. If it is 1, there is a perfect correlation in the sample — there is no difference between the estimated y-value and the actual y-value. At the other extreme, if the coefficient of determination is 0, the regression equation is not helpful in predicting a y-value. |
| sey | The standard error for the y estimate. |
| F | The F statistic, or the F-observed value. Use the F statistic to determine whether the observed relationship between the dependent and independent variables occurs by chance. |
| df | The degrees of freedom. Use the degrees of freedom to help you find F-critical values in a statistical table. Compare the values you find in the table to the F statistic returned by LINEST to determine a confidence level for the model. |
| ssreg | The regression sum of squares |
| ssresid | The residual sum of squares. For information about how ssreg and ssresid are calculated, see “Remarks,” later in this topic. |
⏺ Returns
The LINEST function returns an array of numeric values.
⏺ Available in
Excel for Office 365, Excel 2019, Excel 2016, Excel 2013, Excel 2011 for Mac, Excel 2010, Excel 2007, Excel 2003, Excel XP, Excel 2000.
How to Use LINEST Function in Excel
As this is an array formula, sometimes pressing Enter won’t work. For that, you have to press Ctrl+Shift+Enter. After that, it will return an array of numeric values. After pressing that, our LINEST formula will have brackets ({}).
Look at the following screenshot. It will give you a clear idea.
As you can see, we have entered the LINEST function in cell E5. As this is an array formula, our function has brackets. Here, we got two values including Slope(m) and Intercept(b).
LINEST Function: 4 Practical-life Examples
In the following sections, we will provide you with four suitable and useful examples that will clear your idea about this function. We recommend you learn and practice all these examples to enrich your Excel knowledge.
1. Simple Linear Regression Using the LINEST Function
In statistics, linear regression is a linear approach for modeling the relationship between a scalar reaction and one or more descriptive variables (also known as dependent and independent variables).
A linear regression line has an equation of the form Y = b + mX, where X is the explanatory variable, and Y is the dependent variable. The slope of the line is m, and b is the intercept (the value of y when x = 0).
Take a look at the following screenshot:
Here, we have a dataset of Age and Salary. Our goal is to find the slope and intercept.
📌 Steps
- First, select the range of cells E5:F5.
- Then, type the following formula:
=LINEST(C5:C10,B5:B10,TRUE,FALSE)Here, Age = x and Salary = y
- After that, press Ctrl+Shift+Enter.
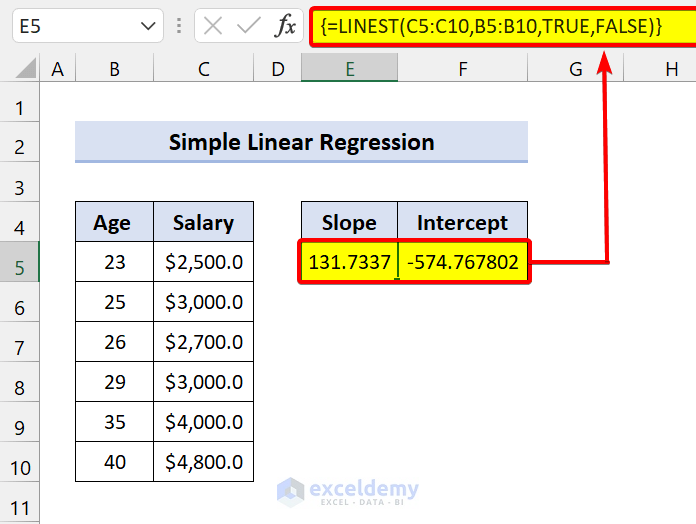
Here, you can see we have a slope of 131.7337. It means that when Age increases by 1, salary increases by $131.7337.
So, if the Age is 24, the salary will be:
Salary = $131.7337*24+(-574.7678)
= $2586.842
So, we have successfully used the LINEST function of Excel here.
2. Multiple Linear Regression in Excel
In Statistics, Multiple linear regression is used to estimate the relationship between two or more independent variables and one dependent variable.
Take a look at the following screenshot:
Here, our equation will be y = m2x2 + m1x1+ b
Where,
y= Salary
m2 = Slope of Experience
m1 = Slope of Age
x2 = Experience
x1= Age
Now, follow these simple steps to find the slopes and intercepts.
📌 Steps
- First, select the range of cells F5:H5.
- Then, type the following formula:
=LINEST(D5:D10,B5:C10,TRUE,FALSE)- After that, press Ctrl+Shift+Enter.
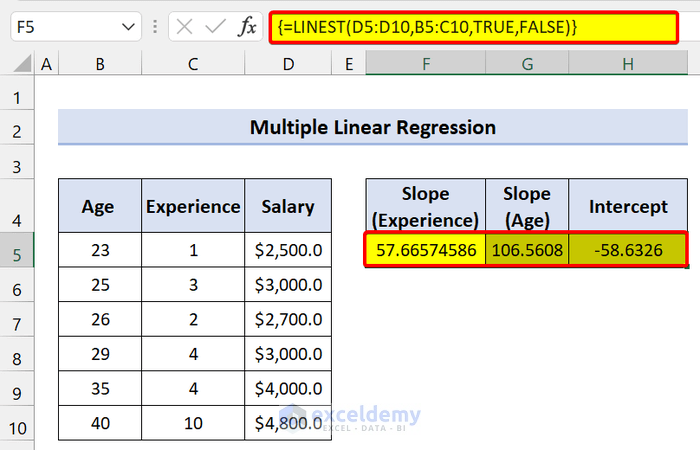
As you can see, we have successfully found all the values using the LINEST function in Excel.
3. LINEST Function to Predict Dependent Variable for Simple Linear Regression in Excel
Apart from computing the slope and intercept for the regression equation, we can use the LINEST function to predict the dependent variable (y) based on the known independent variable (x). To perform this, we can use the LINEST function with the SUM function or the SUMPRODUCT function.
Take a look at the screenshot:
Suppose you want to know the Salary of a person who is 37 years of Age based on previous data. Follow the simple steps to accomplish this.
📌 Steps
- First, type any of the following formulae in cell G5:
=SUM(LINEST(C5:C10,B5:B10,TRUE,FALSE)*(E5:F5))
Or,
=SUMPRODUCT(LINEST(C5:C10,B5:B10,TRUE,FALSE)*(E5:F5))
Or,
=SUMPRODUCT(LINEST(C5:C10,B5:B10,TRUE,FALSE)*{37,1})
- Then, press Enter or Ctrl+Shift+Enter.
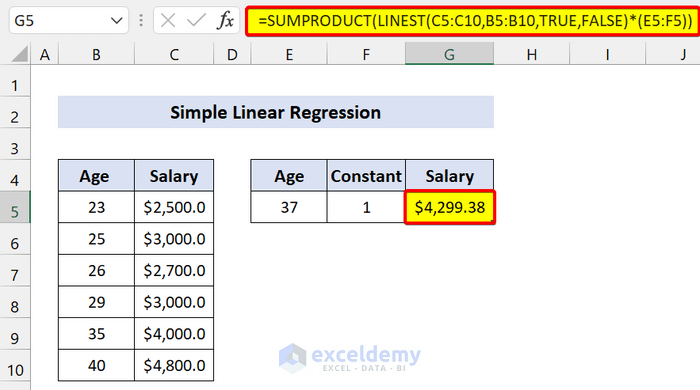
As you can see, we have successfully found the dependent variable salary based on Age using the LINEST function.
To verify this, we are using the y=mx + b formula. Find the Slope and intercept as we showed earlier. Then, type the following formula:
=E8*37+F8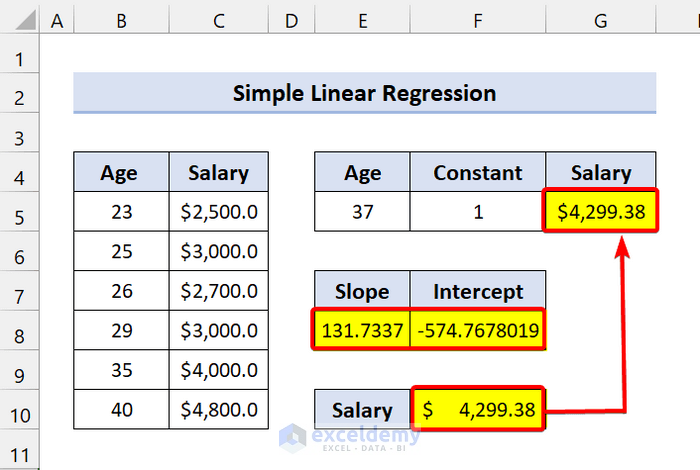
As you can see, the result is the same as before.
4. LINEST Function to Predict Dependent Variable for Multiple Linear Regression in Excel
If you have multiple independent variables (x), you can also find the dependent variable based on this. Here, we are also going to use the LINEST function with the SUM function or the SUMPRODUCT function.
Here, our goal is to find the Salary of a person who is 28 years of age and has 5 years of experience.
📌 Steps
- First, type any of the following formulae in cell I5:
Regular Formula:
=SUMPRODUCT(LINEST(D5:D10,B5:C10,TRUE,FALSE)*(F5:H5))
Or,
Array Formula:
=SUM(LINEST(D5:D10,B5:C10,TRUE,FALSE)*(F5:H5))
Or,
=SUM(LINEST(D5:D10,B5:C10,TRUE,FALSE)*{5,28,1})
- Then, press Enter or Ctrl+Shift+Enter.
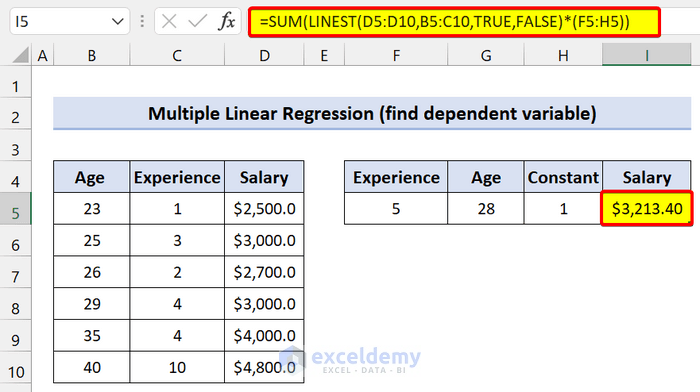
As you can see, we have successfully used the LINEST function to find the Salary based on Experience and Age.
To verify this, we are using the formula: y = m2x2 + m1x1 + b
Find the Slope and intercept as we showed earlier. Then, type the following formula in cell G10:
=F8*5+G8*28+H8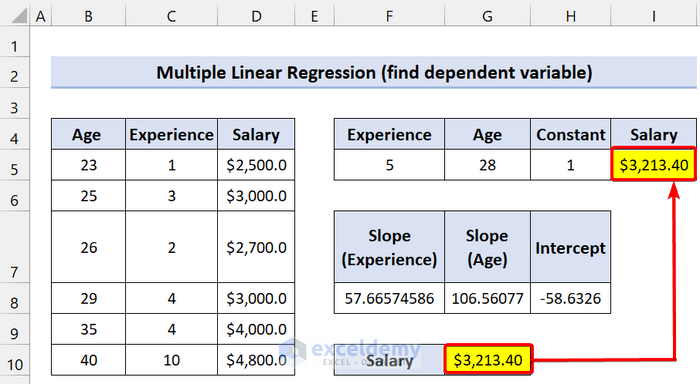
Here, you can see our LINEST function gave the exact result like using the Linear Regression formula.
Additional Regression Statistics by LINEST Function in Excel
If you have read the previous sections, you have noticed that we set the [stats] to FALSE. We did it because we didn’t want additional statistics. If you want the regression analysis, then set it to TRUE.
For simple linear regression, use the following formula:
=LINEST(C5:C10,B5:B10,TRUE,TRUE)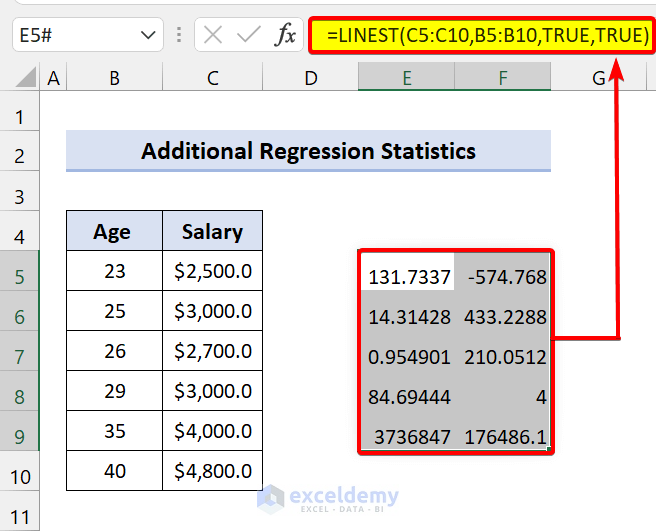
For multiple linear regression, type the following formula:
=LINEST(D5:D10,B5:C10,TRUE,TRUE)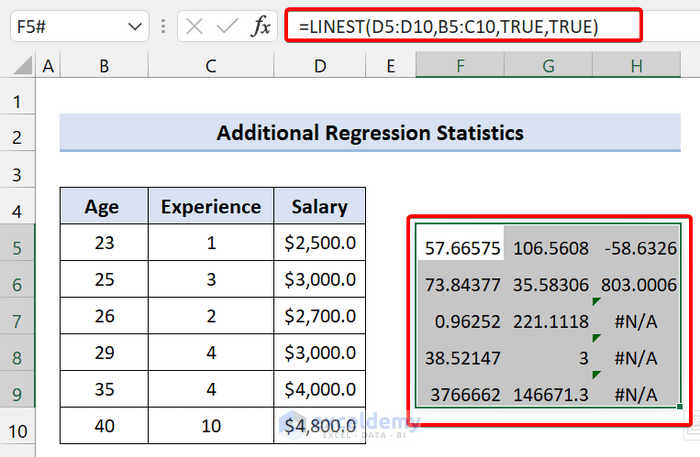
To remove the #N/A error, type the following formula:
=IFERROR(LINEST(D5:D10,B5:C10,TRUE,TRUE),"")Now, look at the following screenshot to know the meaning:
Read More: How to Find Uncertainty of Slope in Excel
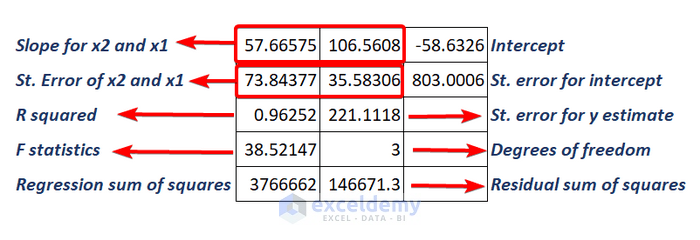
💬 Things to Remember
✎ If you omit the [const] argument, it will be considered TRUE. And our equation will be y=mx+b. But if you set it to FALSE, it will consider the constant 0. And equation will be y=mx.
✎ If the known_x’s and known_y’s ranges have different dimensions, it will show #REF! Error
✎ If known_x’s or known_y‘s contains at least one blank cell, text value, or a text representation of a number, it will show #VALUE! Error
✎ Also, if the const or stats argument cannot be evaluated as TRUE or FALSE, it will show the #VALUE error.
Download Practice Workbook
Download this practice workbook.
Conclusion
To conclude, I hope this tutorial has provided you with a piece of useful knowledge to use the LINEST function in Excel. We recommend you learn and apply all these instructions to your dataset. Download the practice workbook and try these yourself. Also, feel free to give feedback in the comment section. Your valuable feedback keeps us motivated to create tutorials like this.
Keep learning new methods and keep growing!
<< Go Back to Excel Functions | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!
