How to Calculate Volatility in Excel (2 Suitable Ways)

Volatility is a very common term to the investors of the share market. It’s a way to get an idea to invest in a new company. It defines the risk of any stock or security. The higher volatility increases the risk of investment and vice-versa.

In this article, we will discuss the volatility and how to calculate this in Excel with proper explanations.

What Is Volatility?

Volatility is the measure of the fluctuations of return of any stock or security over a time period is called volatility. Volatility is calculated based on the standard deviation or variance of returns over a time period. In the financial market, when the stock index increases or decreases more than 1% over a limited time that is called a volatile market. Simply, volatility is the measure of risk or uncertainty in the stock market.

Types of Volatility:

Volatility is classified into two types. Those are discussed in the below section.

• Historical Volatility:

This calculates volatility based on past information. It predicts the future by analyzing past values. It does not consider future trends, market conditions, or needs. But It is not forward-looking. It is also called historical volatility.

• Implied Volatility:

The implied volatility is forward-looking. It does not care the past performance and considers future expectations. It is also called projected volatility.

How to Calculate Volatility in Excel? (Both Historical and Implied Volatility)

We already discussed two types of volatility. We will explain the calculation of those two kinds of volatility in Excel with explanations.

1. Calculation of Historical Volatility in Excel

Here, we will explain the whole process of calculating the historical volatility. For this, we need to calculate the Standard Deviation. We can calculate the deviation subtraction or LN function of Excel. We will collect stock data from Yahoo Finance. Let’s have a look at the below section for details.

📌 Steps:

• We collected the following sample data.

• We added a row on the right side.
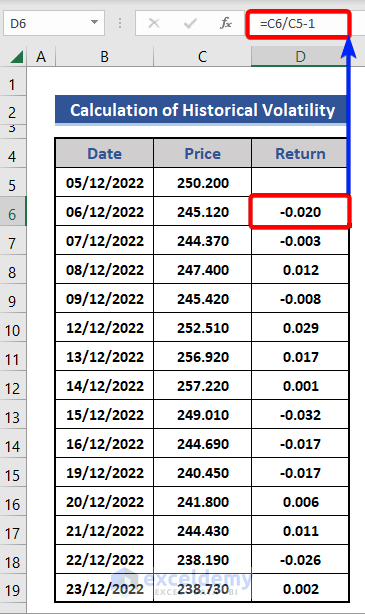
• Use the following formula on cell D6.

Here, we compared the price of the present day with the previous day and subtracted 1. We can also use the following formula based on the LN function.

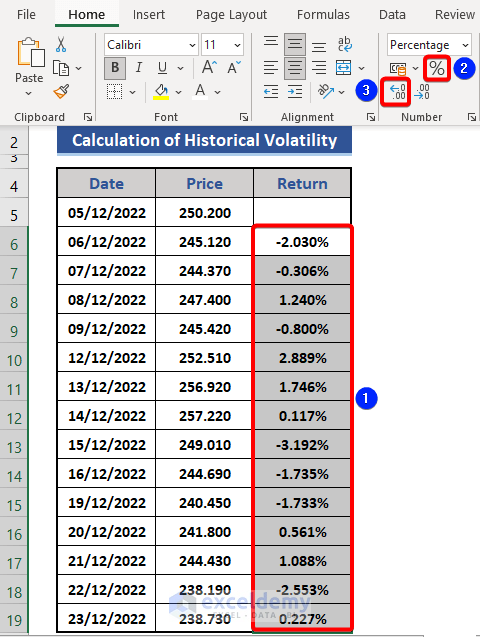
• We need to present the data in percentile form. Select range D6:D19.
• Choose Percentage from the Number group of the Home tab.

Now, increase or decrease the decimal points.

• After that, we will add two new columns to the dataset.

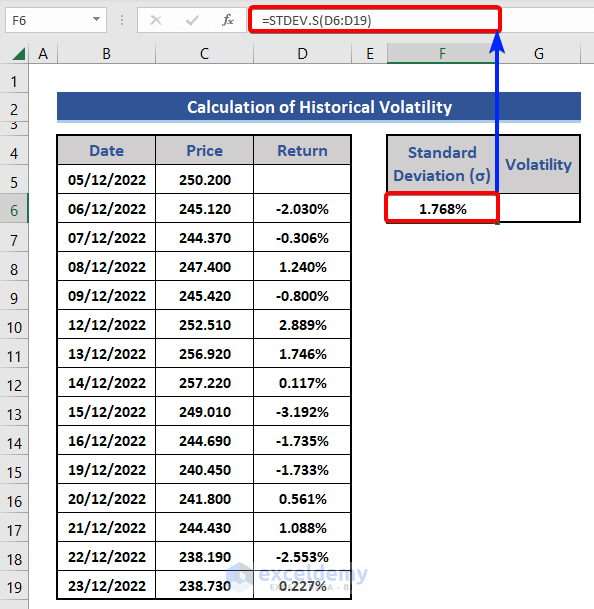
• Put the following formula on cell F6 for standard deviation.

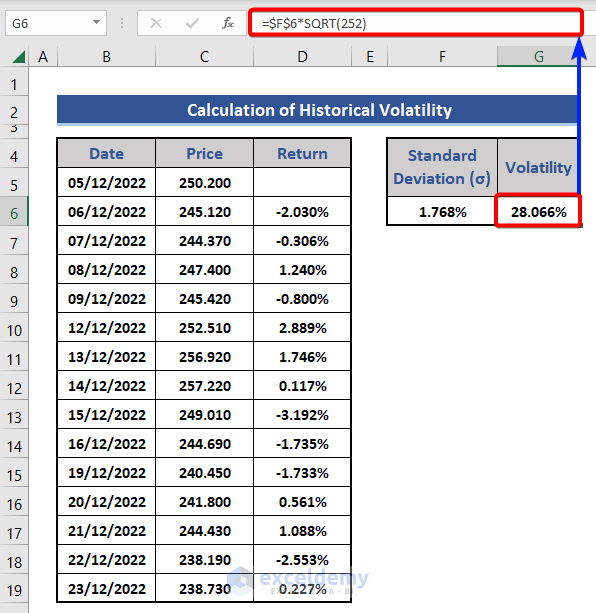
• Finally, we will use the standard deviation to calculate volatility. We will apply the following formula to cell G6.

We calculated the historical volatility. This volatility is also called annualized volatility as we used 252 in the equation. Here, the value of standard deviation is also called daily volatility. If we want to get monthly volatility, we need to use 22. The formula will look like this:

2. Calculation of Implied Volatility

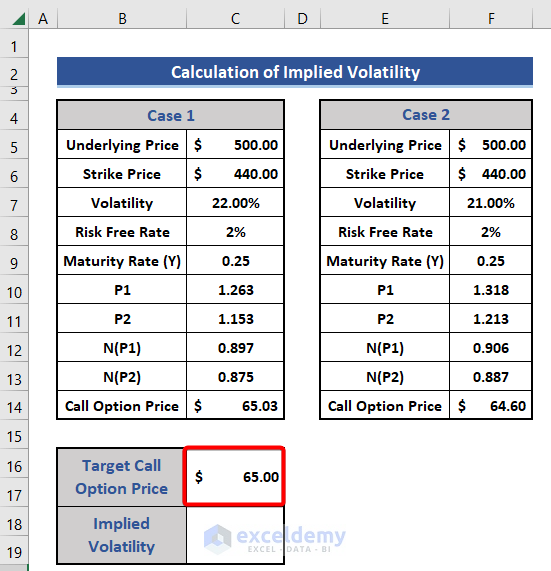
To calculate implied volatility, we need to follow the Black Scholes Model. Using this model, we will calculate the call option price based on the assumed volatility. Further, we will modify the implied volatility until the call option price matches our expectations.

We will use the following based on the Black Scholes Model:

📌 Steps:

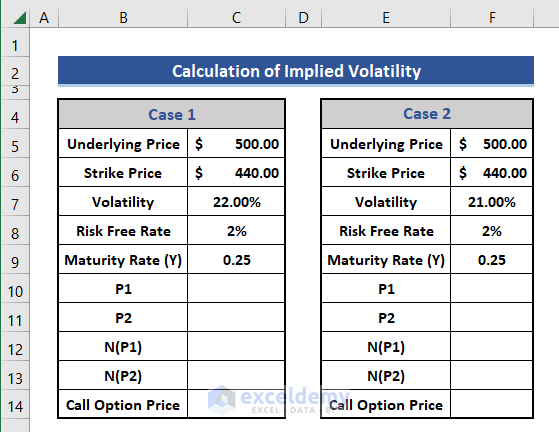
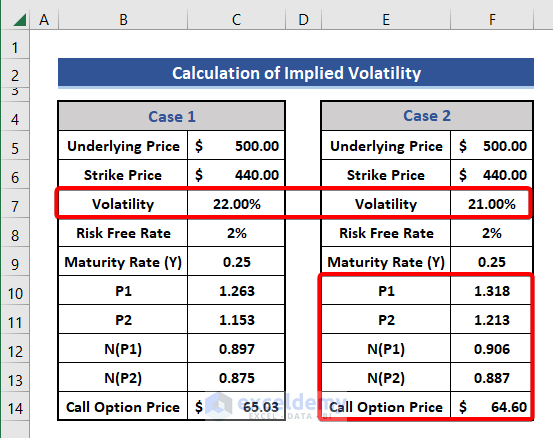
• First, we insert data on Underlaying Price, Strike Price, Volatility, Maturity Time, and Risk-Free-Rate in the dataset for two cases.

The value of volatility is different in the two cases, and the rest are the same.

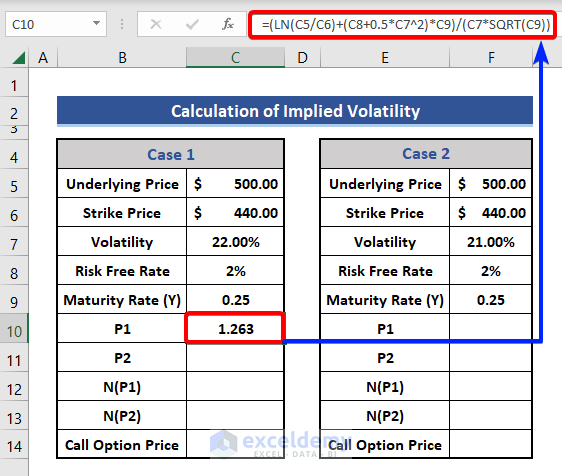
• Now calculate conditional probability, P1 using the following formula.

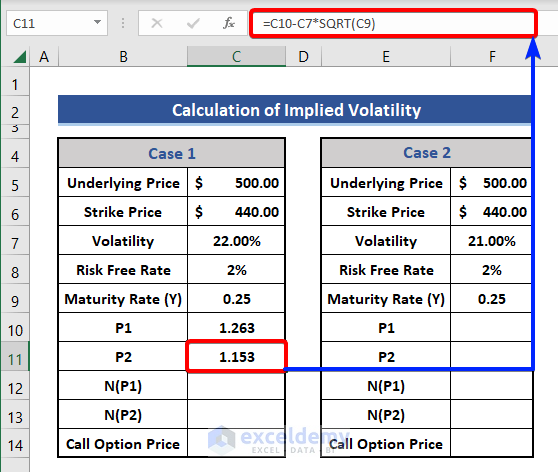
• Now, we will use the SQRT function to calculate probability, P2.

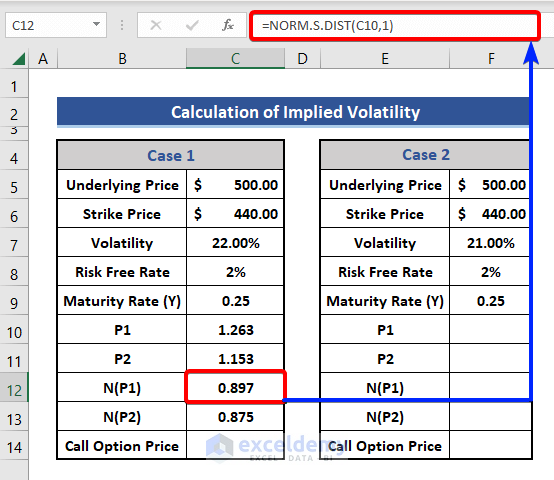
• Now, we will calculate the normalized distribution on cells C12 and C13 using the following formulas.

For Cell C12:

For Cell C13:

We will use the NORM.S.DIST function to calculate the normal distribution in Excel.

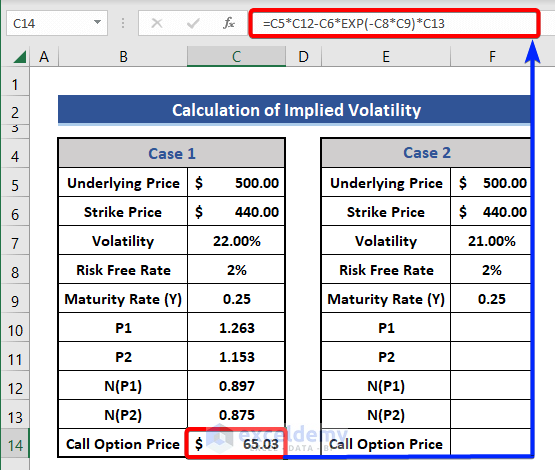
• After that, we will calculate the Call Option Price using the formula.

• Similarly, we perform calculations for Case 2.

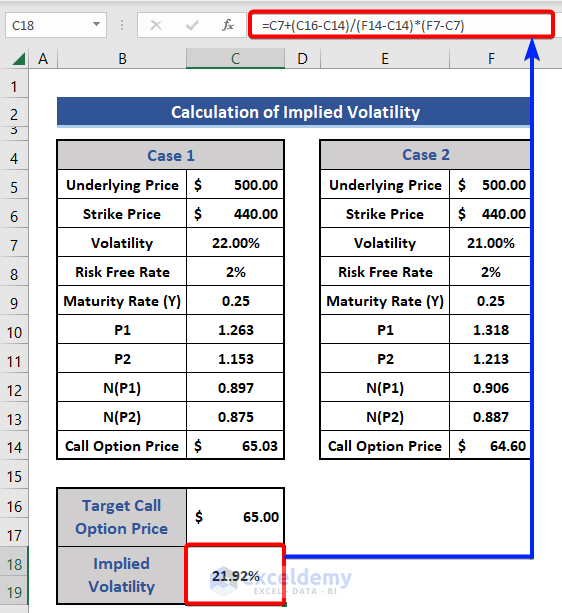
• Now, we add two new rows and set the Target Call Option Price as $65.

• Use the following formula to get the implied volatility based on the Black Scholes Model.

How to Calculate the Volatility of a Portfolio in Excel

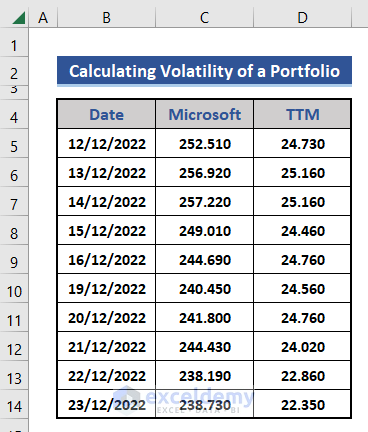
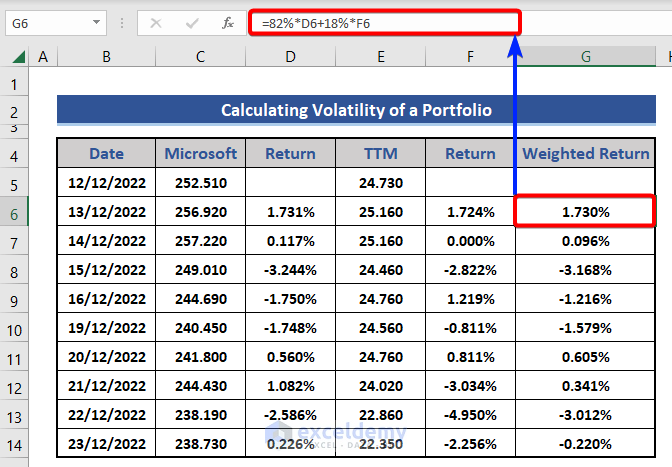
In this section, we will calculate portfolio volatility. For this, we will consider the closing stock price of Microsoft and Tata Motors for the last 10 days. Also, add that weight of Microsoft is 82%, and Tata Motors is 18%. Have a look at the below section.

📌 Steps:

• First, we insert data from Microsoft and Tata Motors into the dataset.

• Then, we add two new columns in the dataset for calculating returns.
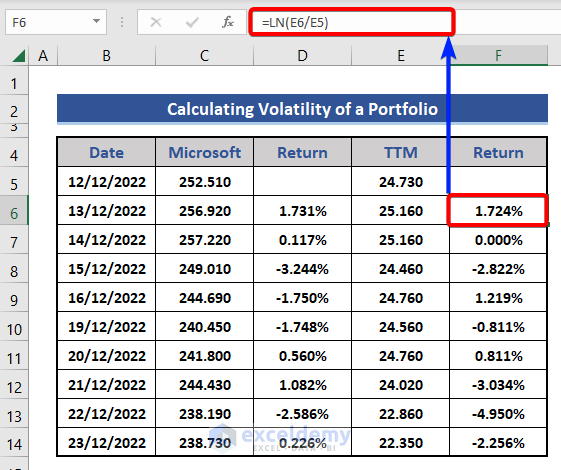
• We will apply the formula based on the LN function to get a return.

For Cell D6:

For Cell F6:

• Now, we will calculate the weighted return. We will multiply the returns by their weight and sum them.

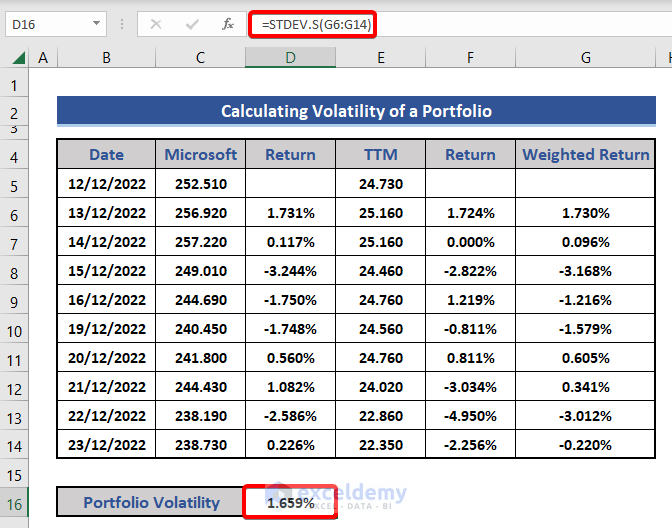
• Then add a new row in the dataset for Portfolio Volatility. Insert the following formula on cell D16.

Finally, we get the portfolio volatility. This is also called daily portfolio volatility. If we want monthly or annualized volatility, then we need to multiply by the square root of 22 and 252 respectively.

Download Practice Workbook

Download this practice workbook to exercise while you are reading this article.

Conclusion

In this article, we described the calculation of two types of volatility in Excel. We also discussed how to calculate portfolio volatility. I hope this will satisfy your needs.

Volatility In Excel: Knowledge Hub

• How to Calculate Volatility for Black Scholes in Excel
• How to Calculate Realized Volatility in Excel
• How to Generate Volatility Surface in Excel

<< Go Back to Excel for Finance | Learn Excel