How to Do Simple Linear Regression in Excel (4 Simple Methods)

When product sellers or producers try to predict amounts or values of future outcomes depending on two or multiple criteria have to conduct Regression Analysis in Excel. To do simple Linear Regression in Excel deal with a single Dependent and Independent variable. There are multiple ways to conduct a Linear Regression Analysis in Excel.

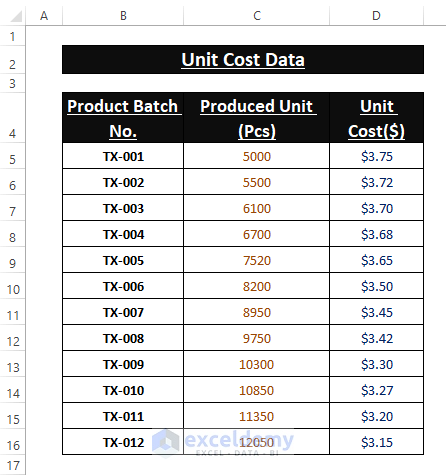
Let’s say we have Unit Cost vs Produced Unit data, and we want simple Linear Regression to identify what criteria really matter.

In this article, we’ll use Add-ins such as Analysis Toolpak and Solver, Excel Graph, and Formulas to do simple Linear Regression in Excel.

What Is Linear Regression?

Regression Analysis comes from Statistics and deals with predicting values that depend on two or more variables. Therefore, Linear Regression estimates values when single dependent and independent variables are concerned. It has an equation of Y=mX+C+E and the variables are

Y = Dependent Variable

m = Slope of the Regression Formula

X = Independent Variable

Ε = Error Term, the difference between the actual value and predicted value.

The error term, E is in the formula because no prediction is never 100% correct. Though some Add-ins calculate errors off-screen, we mention it to clarify the analysis. However, the Linear Regression formula becomes Y=mX+C, if we ignore the error term (i.e., E).

How to Do Simple Linear Regression in Excel: 4 Simple Methods

Method 1: Doing Simple Linear Regression Using Analysis Toolpak in Excel

To conduct Regression Analysis, at 1^st we have to enable Analysis Toolpak. Afterward, we are good to run it.

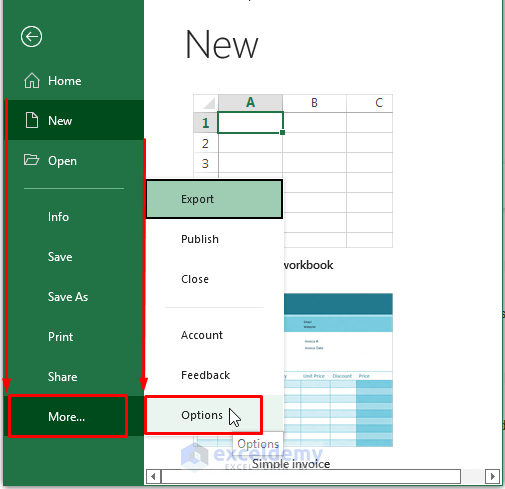
Step 1: Go to Worksheet’s File > Options.

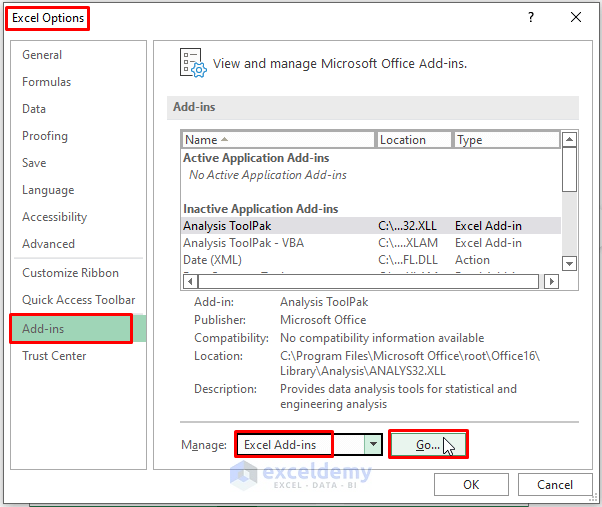
Step 2: In the Options window, Select Add-ins (on the left side of the window) > Choose Excel Add-ins (inside the Manage option) > Click on Go.

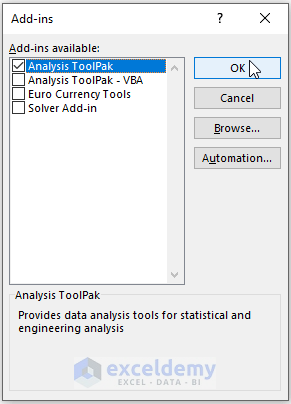
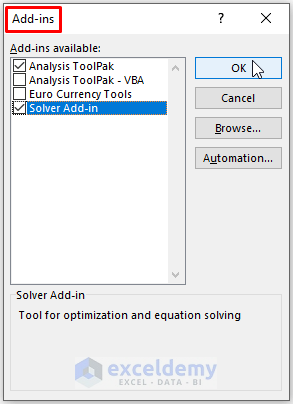
Step 3: The Add-ins window appears. Tick Analysis Toolpak > Click OK.

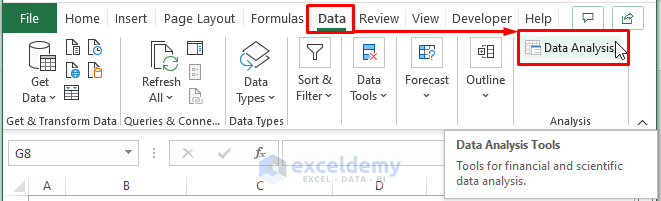
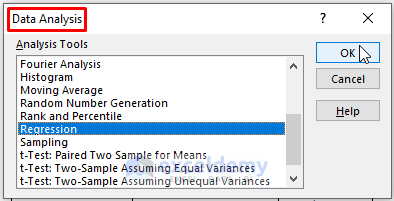
Step 4: After returning to the worksheet, execute Data > Data Analysis (within the Analysis section).

Step 5: Excel brings the Data Analysis command box. Select Regression under the Analysis Tools then click OK.

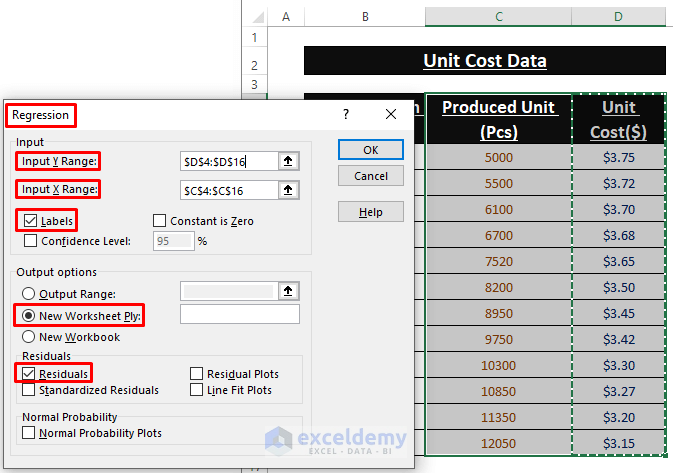
Step 6: In the Regression dialog box, assign cell values to Input Y (i.e., D Column) and X (i.e., C Column) Ranges. Also, tick or choose other preferred options as depicted in the below image.

Linear Regression Analysis Outcome

Conducting a Linear Regression Analysis in Excel is quite easy as Excel does all calculations by itself. Excel results in 4 major parts of analyzed data that hold different values of real-life usage.

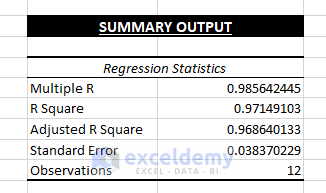
1. Regression Statistics: Regression Statistics is an array of different parameters that indicate how well the measured Linear Regression describes the data model.

⧭ Multiple R: It’s a Correlation Coefficient parameter that indicates a correlation between variables. Its value ranges from -1 to 1. The bigger positive the value, the strong correlative the relationships are. The values indicate:

➤ 1; indicates strong positive bonding or relationship.

➤ -1; indicates strong negative bonding or relationship.

➤ 0; indicates no bonding or relationship.

⧭ R Square: It implies the Coefficient of Determination. It indicates the scale by how well the data model fits the Regression Analysis. Also, it depicts the number of points that fall on the Regression Equation Line. It is calculated using the Total Sum of Squares. As the R² value is 0.9714.., it implies 97.14% of the data value falls in the Regression model and the same percentages of dependent variables are relatable by independent variables. The R² value of more than 95% is taken as a good fit.

⧭ Adjusted R Square: The adjusted value of R² is used in multiple variables Regression Analysis.

⧭ Standard Error: Another parameter that shows a healthy fit of any Regression Analysis. The smaller the Standard Error the more accurate the Linear Regression equation. It shows the average distance of data points from the Linear equation.

⧭ Observations: The iteration number of the data model.

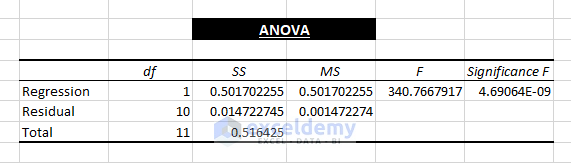
2. ANOVA Outcome: It’s the variance analysis that displays the variability of a data model.

ANOVA divides the Sum of Squares portion into parameters that give information about the shifting within the Regression Analysis. The parameters and their meaning are:

⧭ df: It’s the number of degrees of freedom (i.e., nDOF) related to the variance sources.

⧭ SS: Sum of Squares; SS is considered the good to fit parameter. The less the Residual value of SS against the Total SS value.

⧭ MS: The Mean Square is known as MS.

⧭ F: F statistic or F-test refers to the Null Hypothesis. It tests the overall significance of the regression model.

⧭ Significance F: The P-Value of F.

The ANOVA calculation is less important than conducting a Linear Regression Analysis. However, parameters like Significance F are important for statistically suggesting any data model whether it’s OK or Not. Significance F value less than 5% or 0.05 indicates the healthiness of a data model.

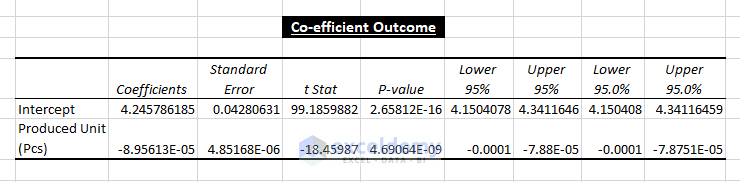
3. Co-efficient Outcome: The most useful part of Regression Analysis is the Coefficient outcome. You can simply use the coefficients to calculate Y values.

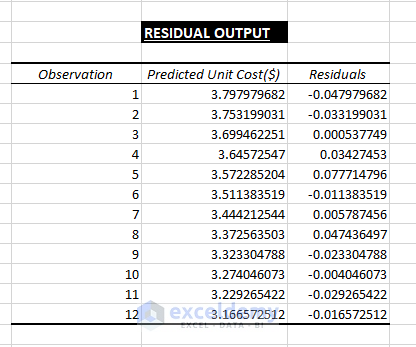
4. Residual Output: It compares the calculated values with the estimated values as depicted in the picture below.

To understand the results more generic way you can visit this result interpretation article.

Method 2: Displaying Linear Regression Equation in Excel Chart

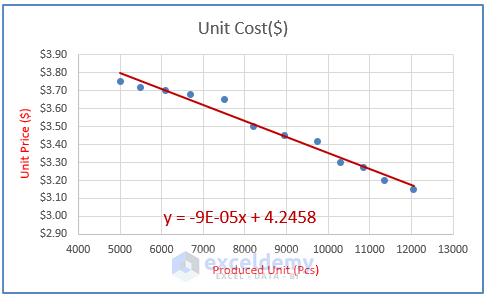
There is a simpler way to depict the relationship between dependent and independent variables; Excel Chart (i.e., Scatter).

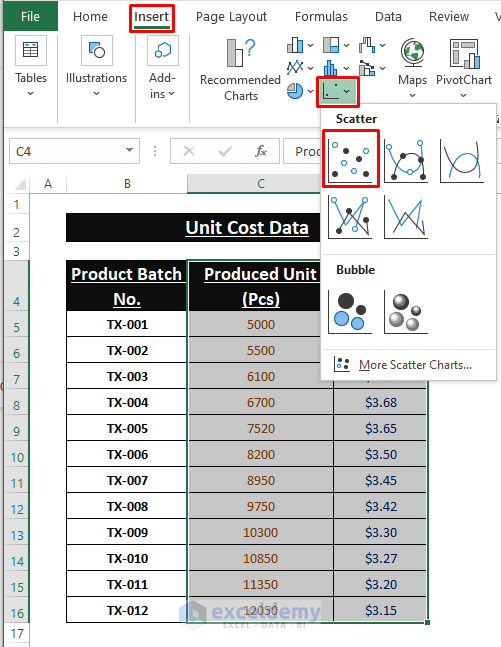
Step 1: Highlight the columns (i.e., Columns C and D), go to Insert > Click on Scatter (inside the Charts section).

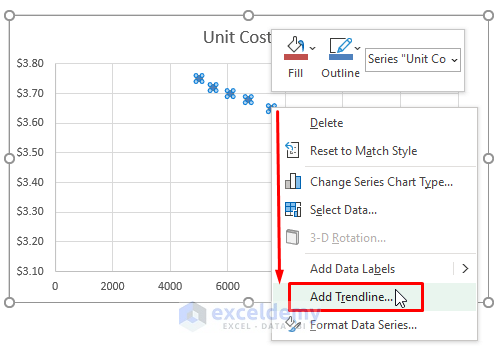
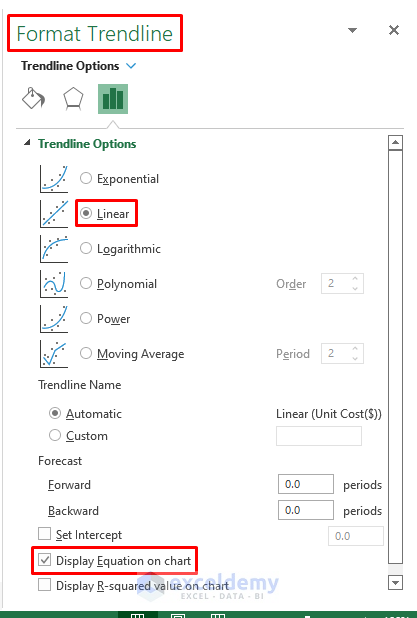
Step 2: Excel immediately inserts the Chart with scatter points. Right-click on one of the points. Select Add Trendline from the Context Menu options.

Step 3: Clicking on Add Trendline fetches the Format Trendline window. Mark and Tick Linear and Display Equation on Chart options respectively.

Step 4: Apply other preferred options from the Format Trendline dialog box. Also, use the Chart Element feature to furnish the Chart as shown in the below picture.

Now, you get the Linear Regression equation from the Chart and its component’s (i.e., m and C) values as expected.

Method 3: Conducting Linear Regression Using Multiple Functions in Excel

Excel’s Statistics functions such as LINEST, SLOPE, INTERCEPT and CORREL calculate components of Linear Regression’s equation.

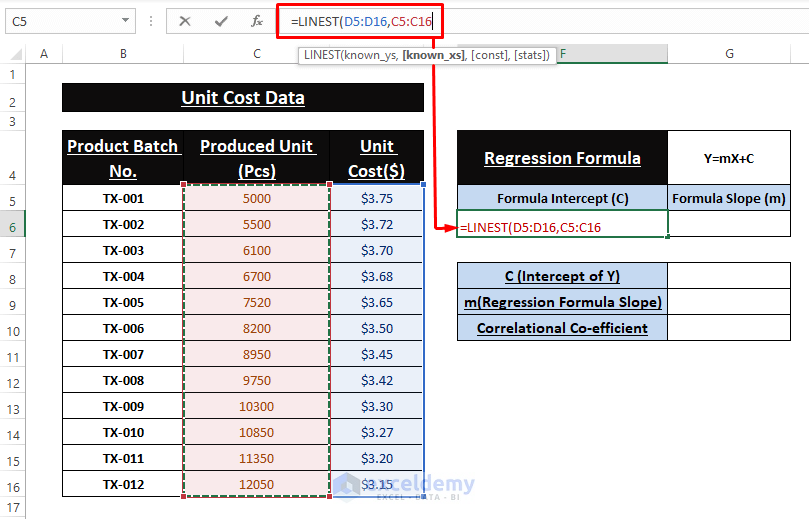
LINEST Function: To describe the relationship between variables, the LINEST function follows the Least Square Regression method. It’s an array function and returns variables (i.e., m and C) of the Linear Regression equation (i.e., Y=mX+C).

🔼 Type the following formula in cell F6.

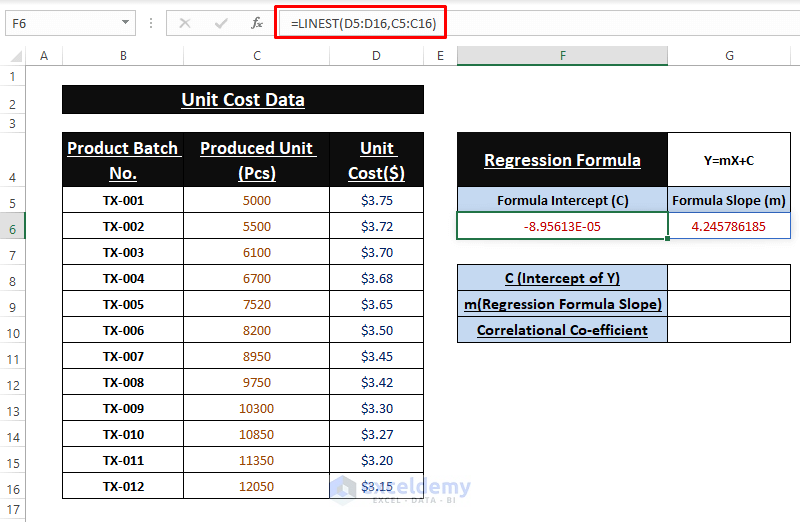
=LINEST(D5:D16,C5:C16)

🔼 As it’s an array formula, use CTRL+SHIFT+ENTER to execute it.

Alternatively, we can use other functions to individually calculate the components of Linear Regression equations.

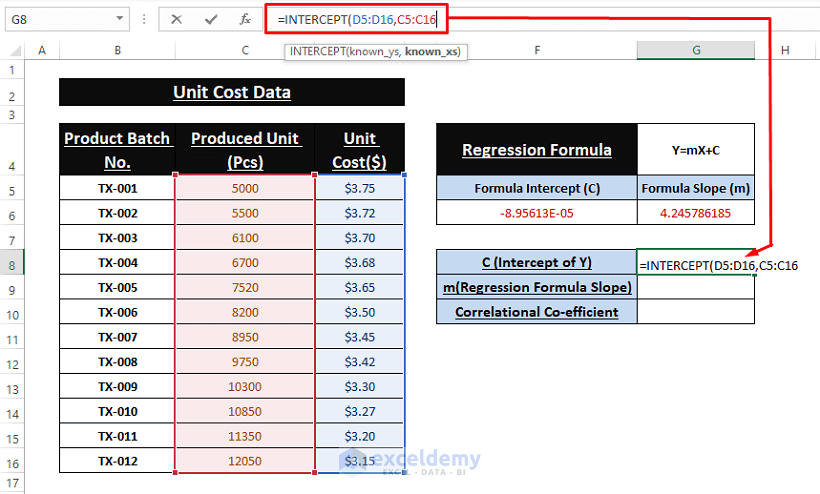
INTERCEPT Function: The INTERCEPT function finds the intercept of Y-axis for the Linear Regression equation. Write the below equation in cell G8 to find the value.

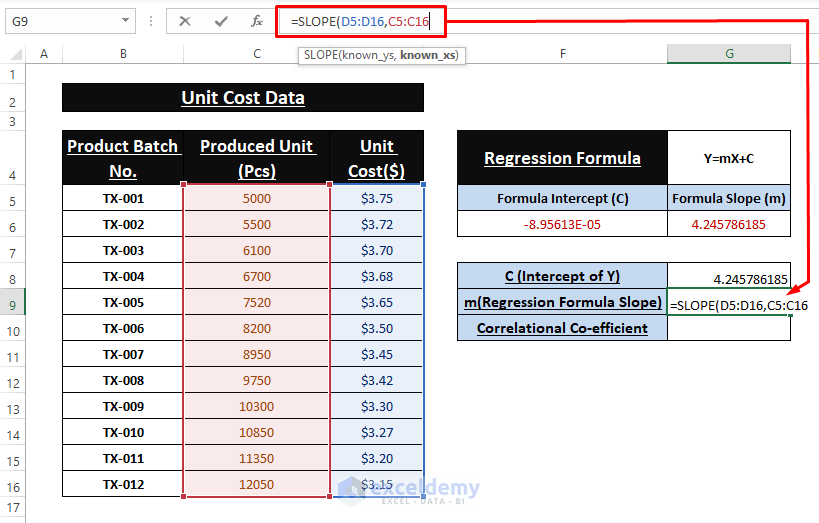
=INTERCEPT(D5:D16,C5:C16)

SLOPE Function: The inclination of the Linear Regression equation is depicted by the slope. Use the below formula to calculate the slope.

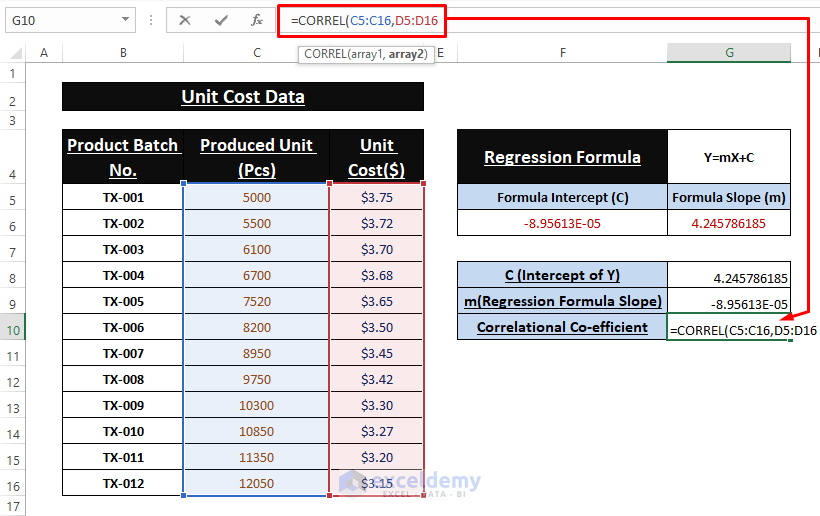
=SLOPE(D5:D16,C5:C16)

CORREL Function: We can find an additional parameter to depict how strongly those two variables are connected. Paste the following formula in cell G10.

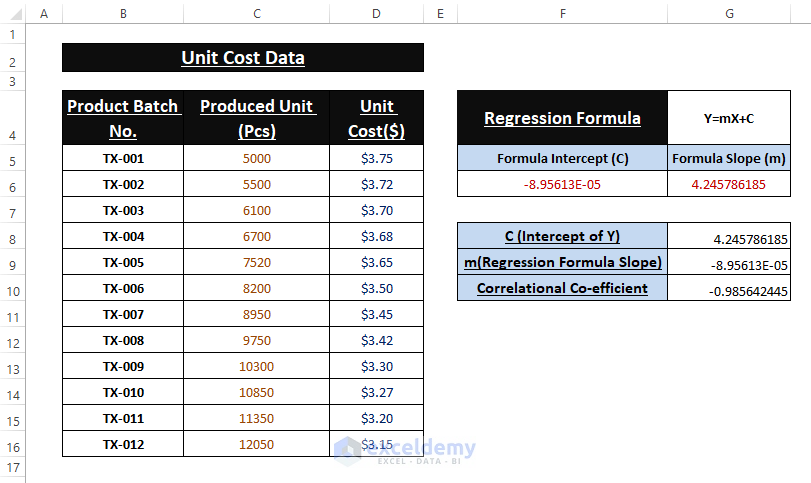
🔼 The latter image displays all the outcomes of the used formulas and thus calculating the Linear Regression.

Read More:

Method 4: Using Solver Add-in to Trial-Error Test Linear Regression Outcomes

This method is complex comparing previous ones. However, this method will clarify what Linear Regression Analysis really means. This method includes some pre-calculation approach before conducting Solver Add-in. The pre-calculation includes:

Use “assumed-value” for the slope (m) and intercept (C) components.
Calculate Ys using those assumed values.
Find the error amount between the newly calculated Ys and Y values.
Use the Solver Add-in to minimize the error.

Follow the latter section for further description.

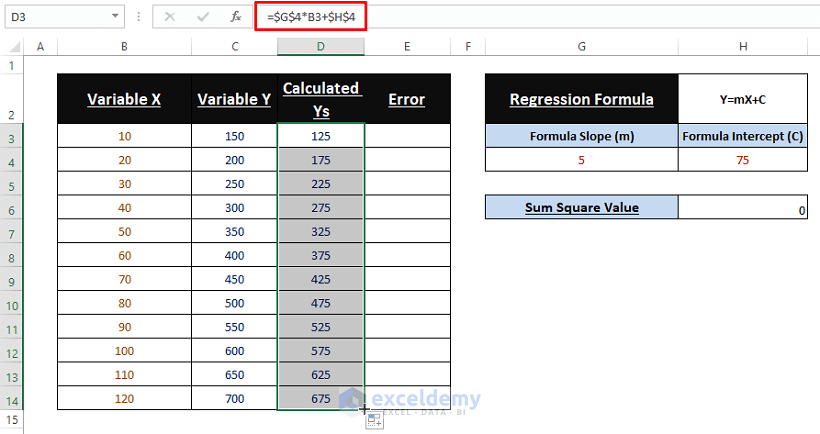
1. Using Assumed Values for Slope (m) and Intercept (C): Input any desired values as Slope (i.e., 5) and Intercept (i.e., 75).

2. Calculating Ys Values: Calculate the new Ys using assumed values as shown in the below image. Use the below formula.

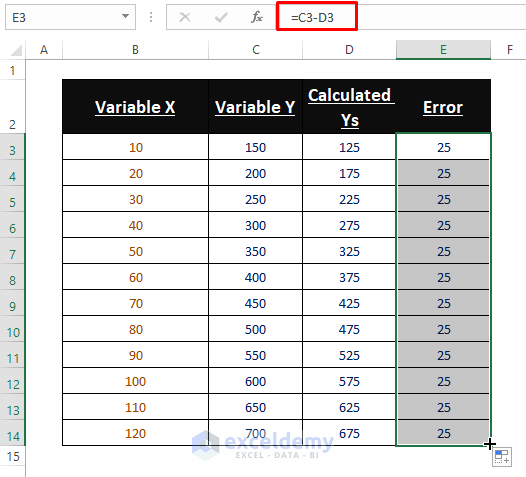
=$G$4*B3+$H$4

3. Error Amounts between Y Values: Execute Arithmetic Operation (i.e., Subtraction) to find error amounts between Ys.

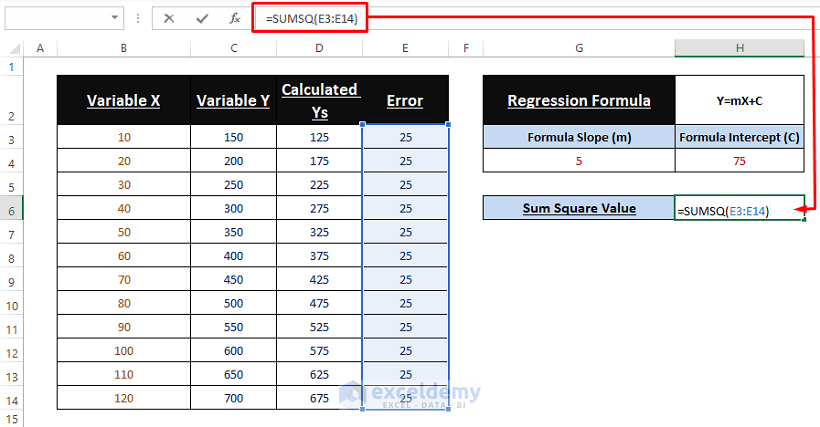
🔼 Also, find the Sum of Squares of the error column. Here, the SUMSQ function is used as a tool in Solver Add-in to minimize the error not wholly drive out. Use the following formula in cell H6.

=SUMSQ(E3:E14)

4. Using Solver Add-in: Now, 1st enable the Solver Add-in following Method 1 instructions.

🔼 Afterward, go to Data > Click on Solver (inside the Analysis section).

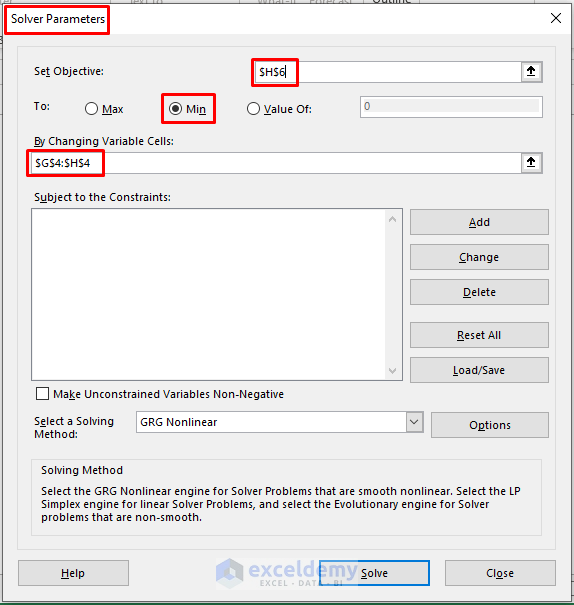
🔼 In a moment, the Solve Parameters dialog box opens. In the dialog box,

➤ Assign Set Objective as H6 (where the Sum of Square value resides).

➤ Mark Min as To.

➤ Insert Slope (m) and Intercept (C) variable values under By Changing Variable Cells.

➤ Click on Solve.

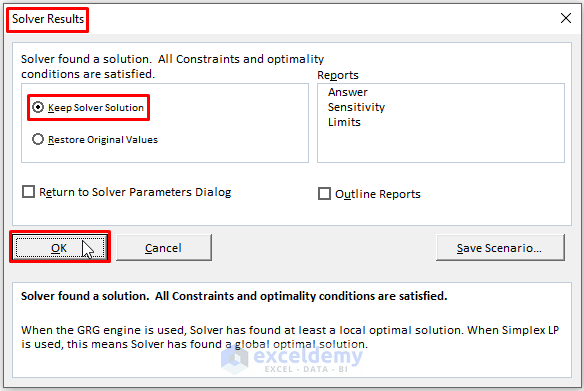
🔼 Instantly, Excel shows the Solver Results window. Mark the Keep Solver Solution option then Click on OK.

The outcome includes estimated Y values after conducting Linear Regression Analysis.

Download Excel Workbook

Linear Regression Analysis.xlsx

Conclusion

In this article, we demonstrate multiple methods to do simple Linear Regression in Excel. However, each mentioned methods have its own convenience. Hope these above-mentioned methods provide you, with your desired one to go by. Comment, if you have further inquiries or have anything to add.

<< Go Back to Regression Analysis in Excel | Excel for Statistics | Learn Excel

Get FREE Advanced Excel Exercises with Solutions!