How to Interpret Multiple Regression Results in Excel

Often you may execute Multiple Regression Analysis in Excel. But you may get troubled to understand the terms used in the regression analysis. In this article, I’ll discuss in detail how to interpret multiple regression results in Excel with a real-life example.

What Is Multiple Regression?

When the number of independent variables is two or more while doing linear regression, it is called multiple linear regression analysis. The equation for calculating multiple regression analysis is as follows.

y=b+b₁X₁+b₂X₂+....b_nX_n

Where

Y is the dependent variable

b is the intercept

X₁ and X₂ are the independent variables

b₁ and b₂ are coefficients of the corresponding independent variables.

How Can You Do Multiple Regressions in Excel

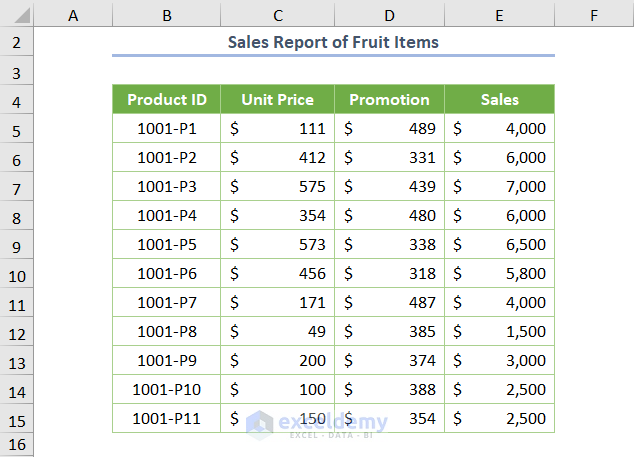
Let’s say, you have the following dataset where Sales Report is given with Unit Price, Promotion (for advertisement), and Sales.

Now, you need to run the multiple regression model to find the relationship between the dependent variable (Sales) and the independent variables (Unit Price and Promotion).

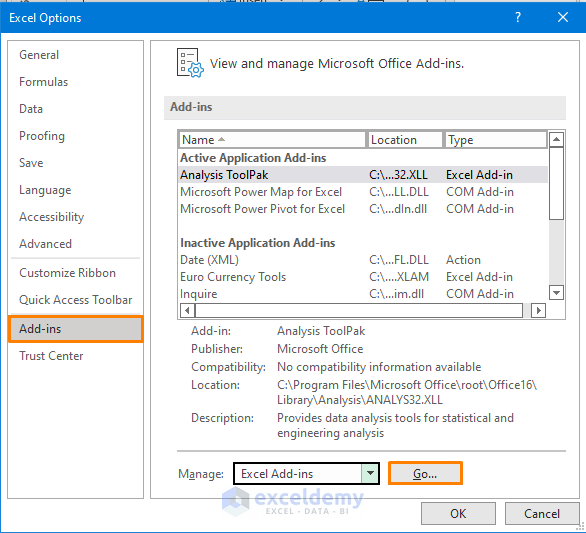
Whatever, to run the regression model, you need the Data Analysis command in Excel. If you don’t have it in the ribbon by default, you may add it the following way.

Firstly, go to File > Options.
In the Excel Options, navigate to the Add-ins and press the Go button.

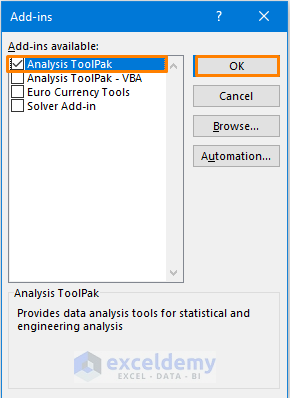
Next, check the Analysis ToolPak and press OK.

Now, you’re ready to run the regression model for the above dataset in Excel.

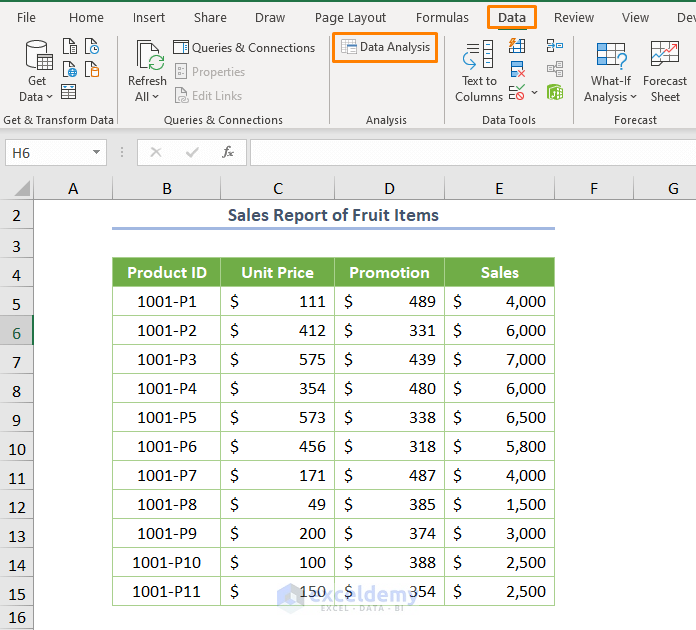
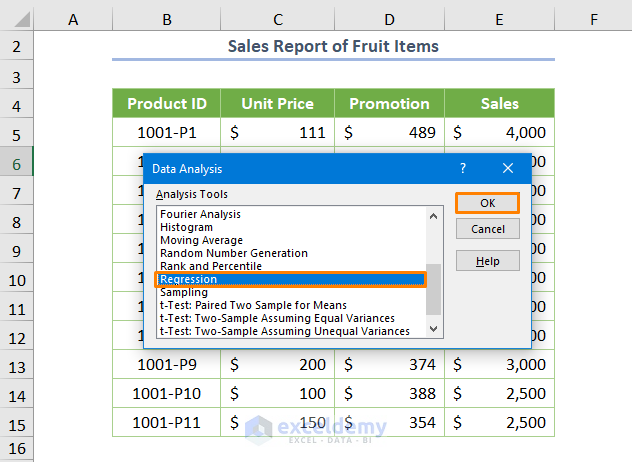
Initially, select the Data Analysis command from the Data tab.

And, pick the Regression tool.

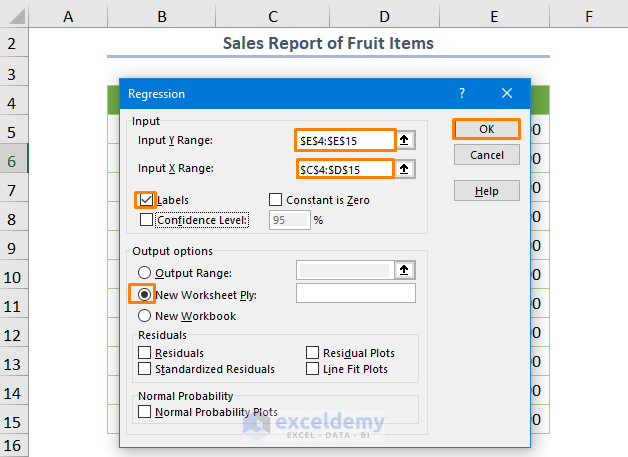
Later, specify the Input Y Range as $E$4:$E$15 and Input X Range as $C$4:$D$15. Also, check the box before Labels and press OK.

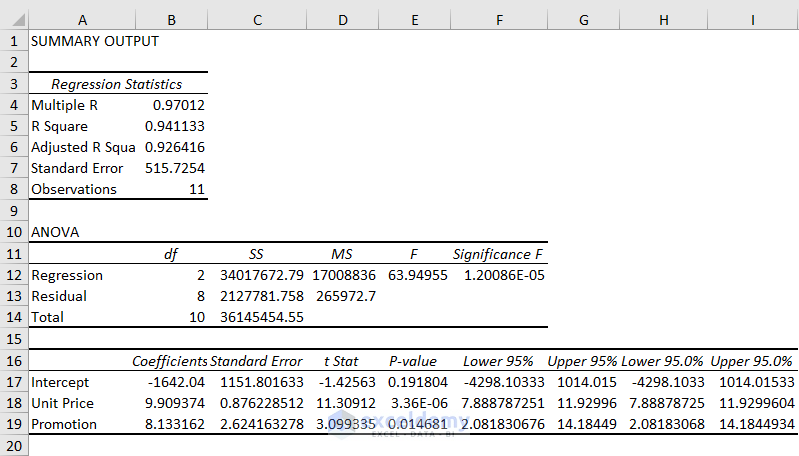
Eventually, you’ll get the following output.

1. Interpreting Results of Multiple Regression Statistics Table in Excel

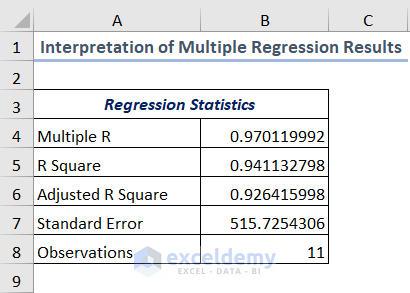
If you closely look at the upper portion of the regression output, you’ll get a table titled Regression Statistics as shown in the below screenshot.

Now, let’s try to understand the terms.

Multiple R (Correlation Coefficient): Multiple R refers to the degree of linear relationship among the variables. The following table may help you to understand the term better.

Value of Multiple R	Refers to
1	Strong positive relationship
0	No relationship
-1	Strong negative relationship

R Square (Coefficient of Determination): R Square reveals the goodness of fit. That means how many points fit with the regression line. The higher the value of R Square, the better-fitted the regression line you’ll get. Here, the value of R Square represents an excellent fit as it is 0.94. It means that 94% variation in the dependent variable can be explained by the independent variable. In the case of multiple regression relationships, you have to keep attention to the Adjusted R square.
Adjusted R Square: Adjusted R Square is fruitful when you have two or more independent variables. As it provides the comparison among the variables which one is more important than the other. The value will be higher than the R Square if a new independent variable improves the model or vice versa. In this dataset, the value of the Adjusted R Square is 0.92. That means 92% of the points fit the regression line.
Standard Error: Simply, the Standard error tells about the precision of your multiple regression analysis.
Observations: It shows the number of products which is 11.

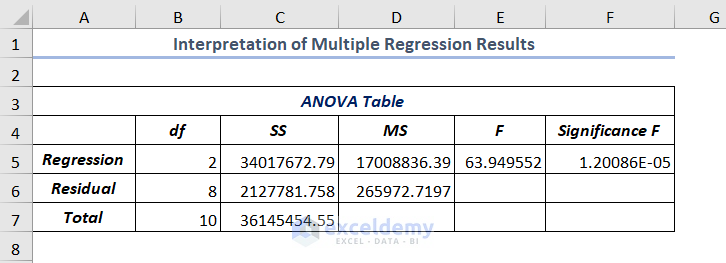
2. Interpreting Regression Results of ANOVA Table in Excel

Moreover, in the middle of the output, you’ll see the ANOVA (Analysis of Variance) Table.

The terms used in the table are as follows.

df (degrees of freedom): df refers to degrees of freedom. It can be calculated using the df=N-k-1 formula where N is the sample size, and k is the number of regression coefficients.
SS (Sum of Squares): The Sum of Squares is the square of the difference between a value and the mean value. The higher the value of the Sum of Squares refers to higher variation in the values or vice-versa.
MS (Mean Squares): Mean Squares is mainly the mean of the square of the variation of an individual value and the mean value of the set of observations.
F (F-test): F or F statistic provides the overall importance of the regression model for the null hypothesis. If you divide the MS of regression by the MS of Residual, you’ll get the F-test.
Significance F: Significance F is a crucial term to find the output of your model whether it is statistically significant or not. When the value of the Significance F is not greater than 0.05, the independent variables have a statistically significant relationship with the dependent variable. Here, it is 0.00001 which represents there is a significant relationship between the Unit Price and Promotion (x values) and Sales (y values).

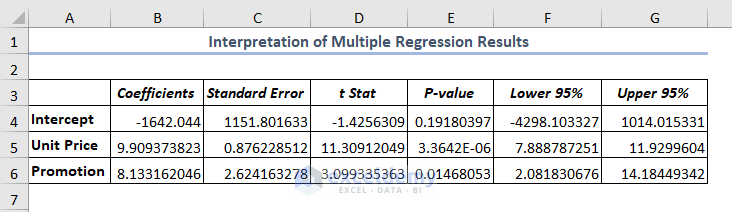
3. Interpreting Results of Multiple Regression Coefficients Table in Excel

Let’s have a look at the last portion where you have to know the following terms.

Coefficients: Coefficients are calculated using the least square method. In this example, the regression equation will be-

y(Sales)=-1642.04 + 9.91*Unit Price + 8.13*Promotion

Standard Error: Simply it is the standard deviation of least square estimates.
t Stat: t Stat refers to the coefficient being equal to zero in the case of the null hypothesis.
P-value: The P-value shows the statistically significant relationship between the independent and dependent variables. Here, P-value for Unit Price is 0.000003 which is below 0.05. So, Unit Price is statistically significant with the Sales.
Lower 95%: It means the lower limit when the confidence interval is 95%.
Upper 95%: It is the upper limit of the confidence interval.

Download Practice Workbook

Interpretation of Multiple Regression Results.xlsx

Conclusion

That’s the end of today’s session. I firmly believe this article will be highly beneficial for you to interpret the multiple regression results found in Excel. Anyway, don’t forget to share your thoughts.

<< Go Back to Regression Analysis in Excel | Excel for Statistics | Learn Excel

Get FREE Advanced Excel Exercises with Solutions!