Naimul Hasan Arif
Sometimes we try to predict the future outcome based on the past records. Regression Analysis is exactly the one which helps to predict the future. In this article, we are going to discuss on how to do Linear Regression in Excel.
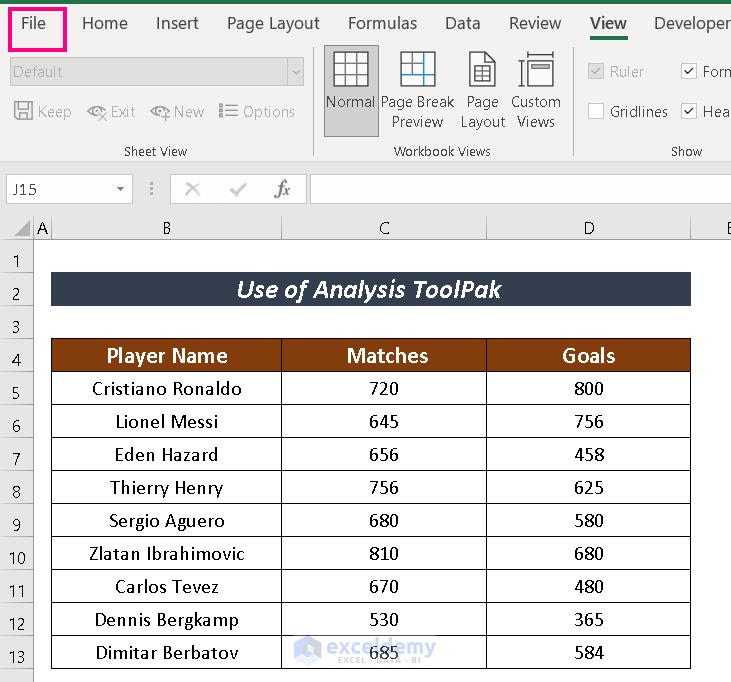
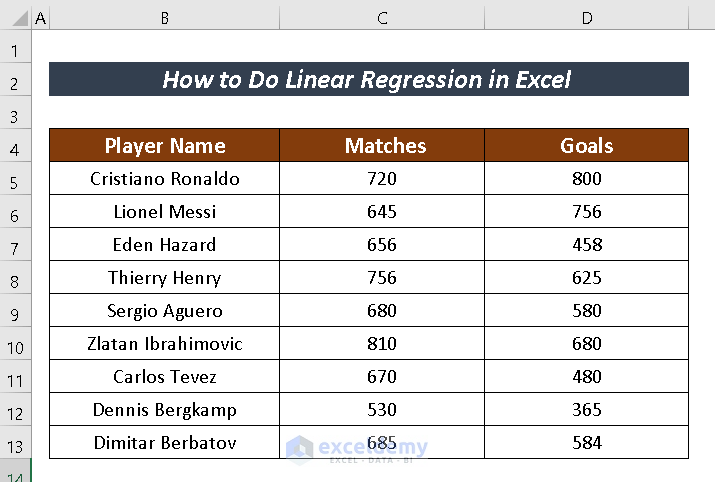
For more clarification, I am going to use a Dataset containing Player Name, Matches, and Goals columns to find the Linear Regression between Matches vs Goals.
Download Practice Workbook
Basics of Linear Regression
Regression Analysis is a part of Statistics which helps to predict values depending on two or more variables. Linear Regression helps to estimate values between a single independent and dependent variable.
The equation used here is :
Y = mX + C + EWhere,
Y = Dependent Variable
m = Slope of the Regression Formula
X = Independent Variable
Ε = The Error which is the difference between the actual value and predicted value.
The error term, E is in the formula because no prediction is fully accurate. Though some Add-ins calculate errors off-screen, we mention it to clarify the analysis. However, the Linear Regression formula becomes Y=mX+C, if we ignore the error term.
4 Simple Ways to Do Linear Regression in Excel
1. Using Analysis ToolPak to Do Linear Regression
Analysis ToolPak is the best tool to do Linear Regression.
Steps:
- Go to File.
- Then, select Options.
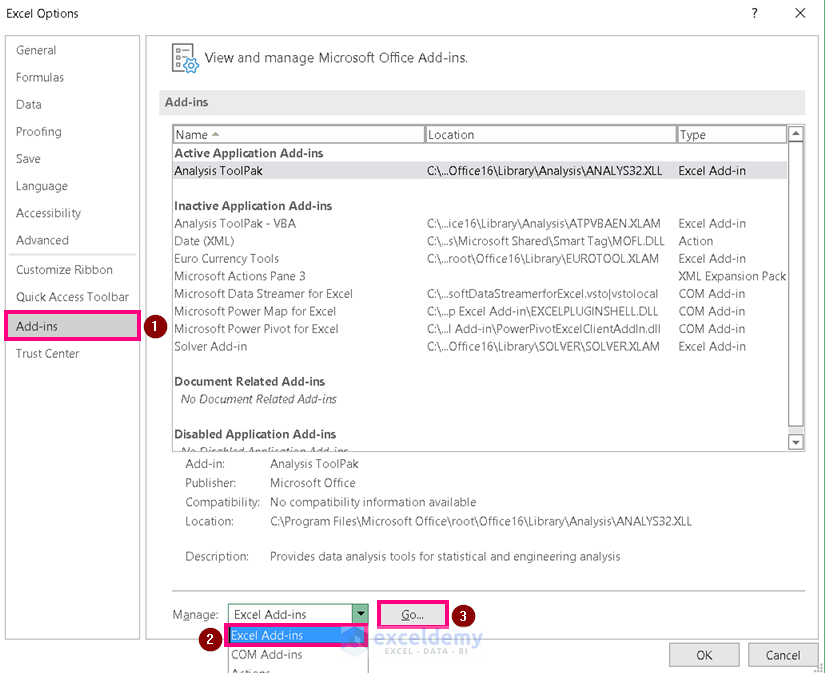
- Click on Add-ins.
- Then, choose Excel Add-ins and click on Go.
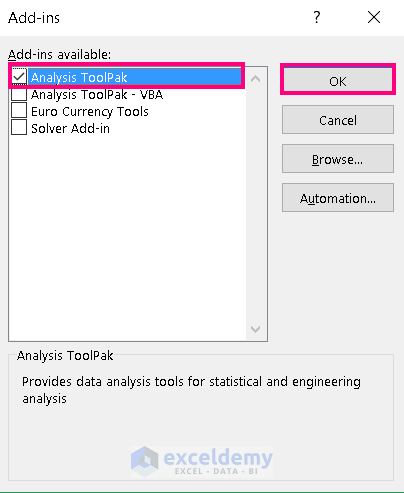
- Check one Add-in at a time and press OK.
- Now, go to Data —> Data Analysis.
- From Analysis Tools, choose Regression and press OK.
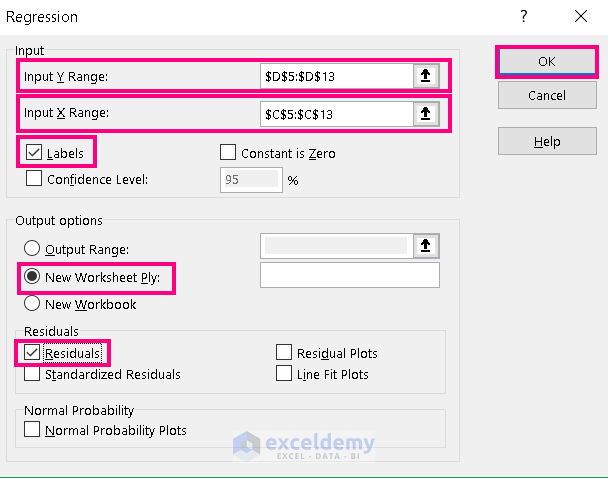
- Now, Assign values in the Input Y Range ( e. D5:D13), Input X Range (i. e. C5:C13).
- Check the boxes named Labels, New Worksheet Ply, and Residuals.
- Finally, hit OK.
Then, we will have 4 major Linear Regression Analysis Outcomes in a new window.
4 Major Linear Regression Analysis Outcomes
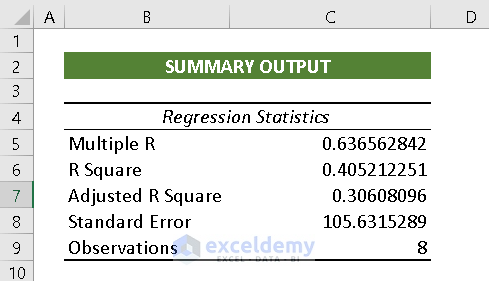
- Regression Statistics: Regression Statistics is an array of various parameters that describe how well the measured Linear Regression is.
Multiple R: Multiple R is a Correlation Coefficient parameter that indicates the correlation between variables. Its value ranges from -1 to 1. The bigger positive the value, the stronger correlative the relationships are.
R Square: It symbolises the Coefficient of Determination. It indicates the scale by how well the data model fits the Regression Analysis.
Adjusted R Square: The value of R^2 is used in multiple variables Regression Analysis.
Standard Error: Another parameter that shows a healthy fit of any Regression Analysis. The smaller the Standard Error the more accurate the Linear Regression equation. It shows the average distance of data points from the Linear equation.
Observations: The number of iterations in the data model.
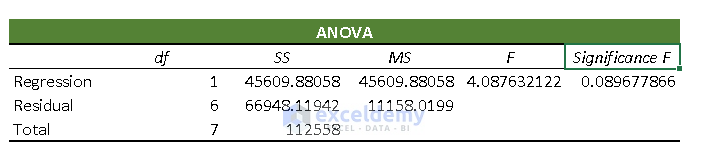
- ANOVA: It analyses the variance of the data model.
df: df expresses the Degrees of Freedom.
SS: SS (Sum of Squares) symbolizes the good to fit parameter.
MS: It means the Mean Square.
F: F refers to the Null Hypothesis. It tests the overall significance of the regression model.
Significance F: The P-Value of F.
- Co-efficient Outcome: It helps to calculate the Y values quite easily.
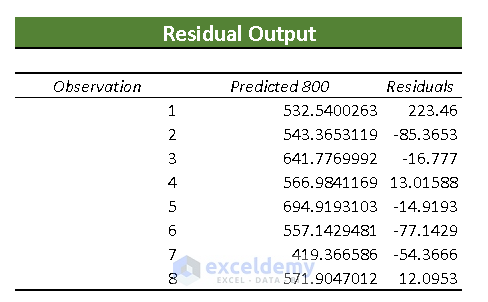
- Residual Output: It compares the estimated value with the calculated value.
Read More: Multiple Linear Regression on Excel Data Sets (2 Methods)
2. Applying Excel Chart to Do Linear Regression
Excel Chart is quite simple to do Linear Regression.
Steps:
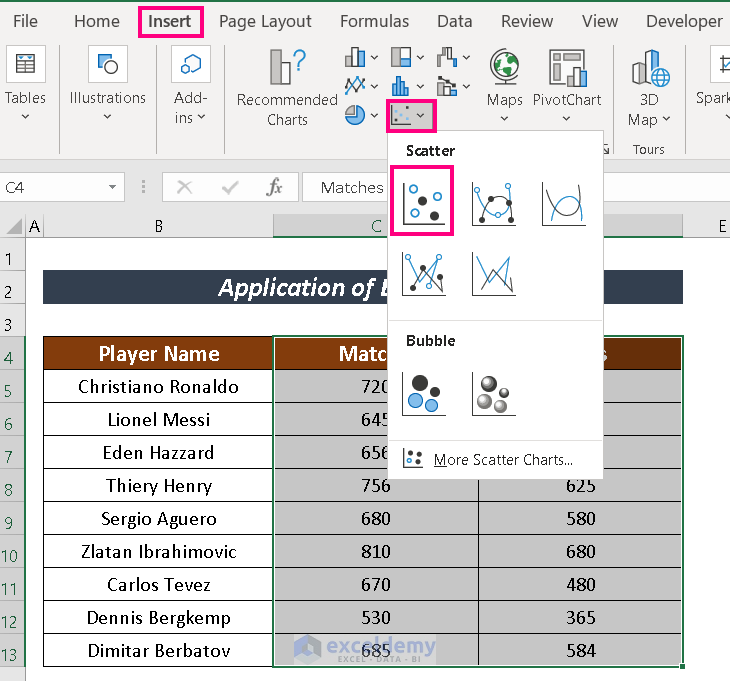
- Select the cells to analyze. Here, I selected cells C4:D13.
- Go to Insert and click on Scatter.
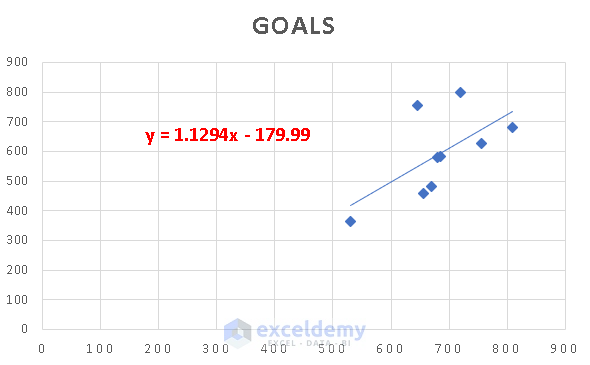
Excel will show the scattered point.
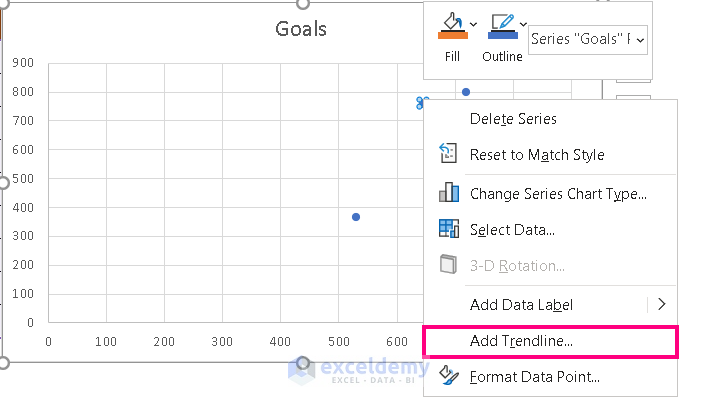
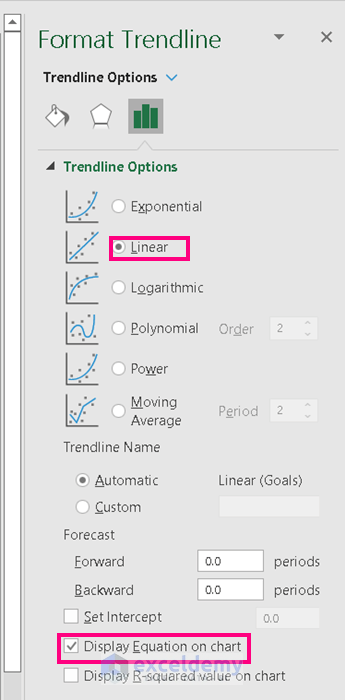
- Now, Right-click on the scattered point and choose Add Trendline.
- From the Format Trendline box, check Linear and Display Equation on chart.
Finally, we have the Regression Line along with the equation.
Similar Readings
- How to Do Multiple Regression Analysis in Excel (with Easy Steps)
- How to Interpret Regression Results in Excel (Detailed Analysis)
3. Formulas to Do Linear Regression
We can also employ Formulas to have Linear Regression. We are going to apply the INTERCEPT Function and SLOPE Function to find out the unknown
Steps:
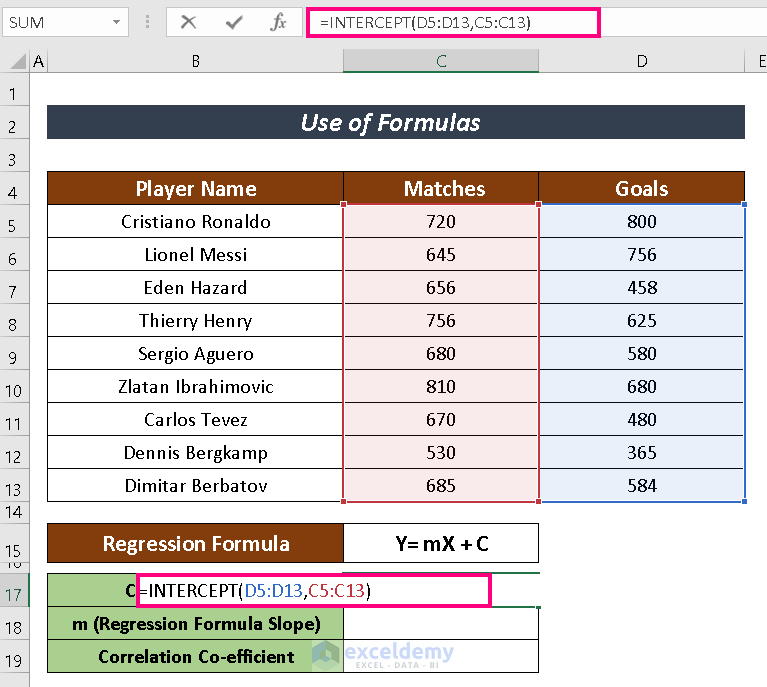
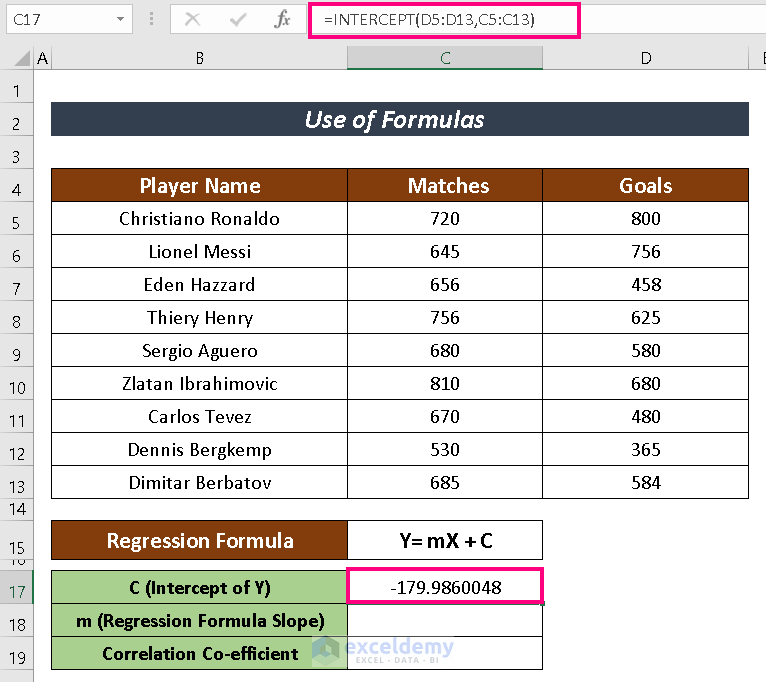
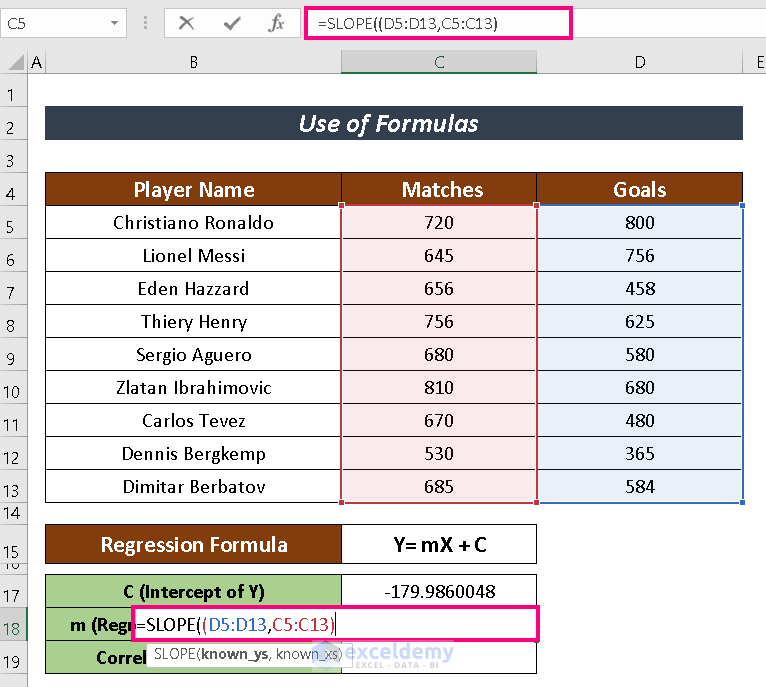
- Input the following formula in a selected cell to have the value of C which represents the intercepted value of Y-axis.
=INTERCEPT(D5:D13,C5:C13)
- Hit ENTER to have the result.
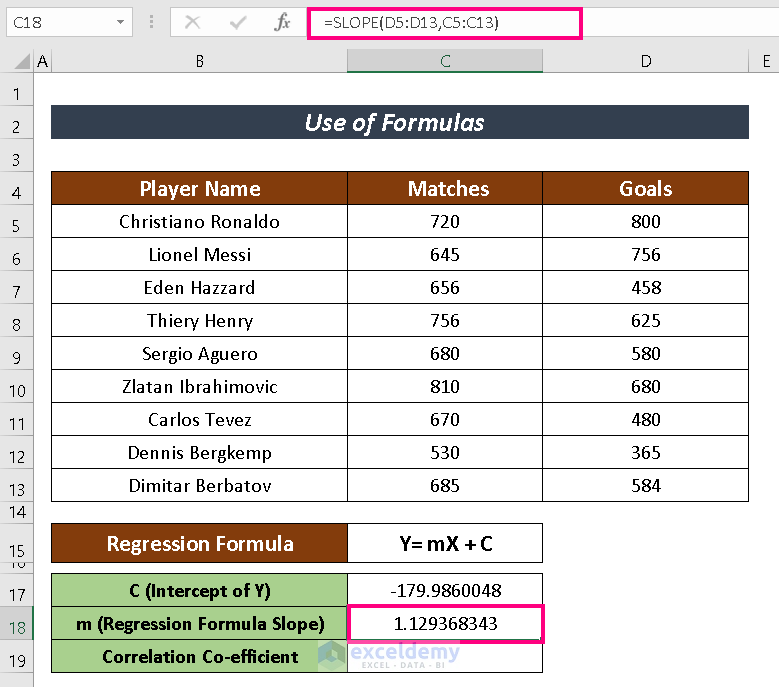
- Again, input the following formula in a selected cell to have the value of the slope m.
=SLOPE(D5:D13,C5:C13)
- Now, press ENTER.
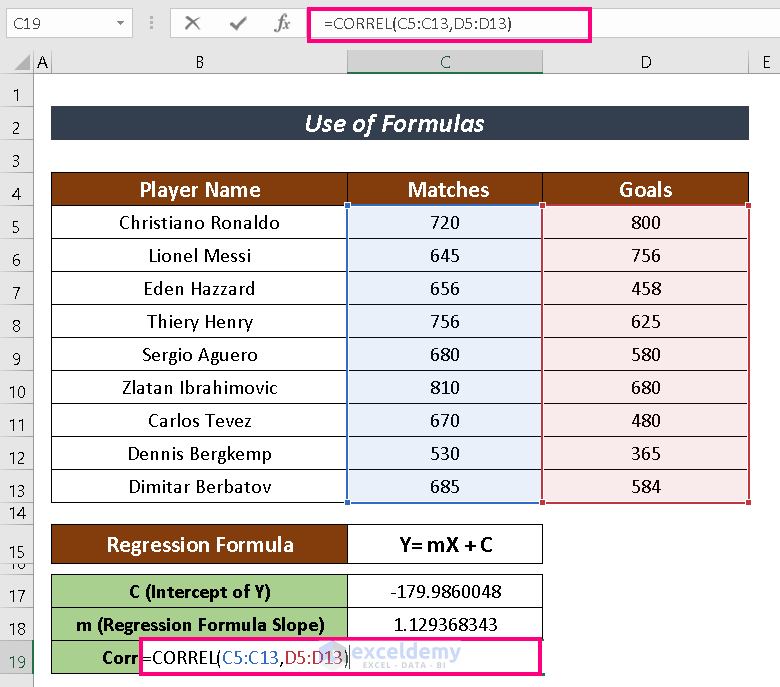
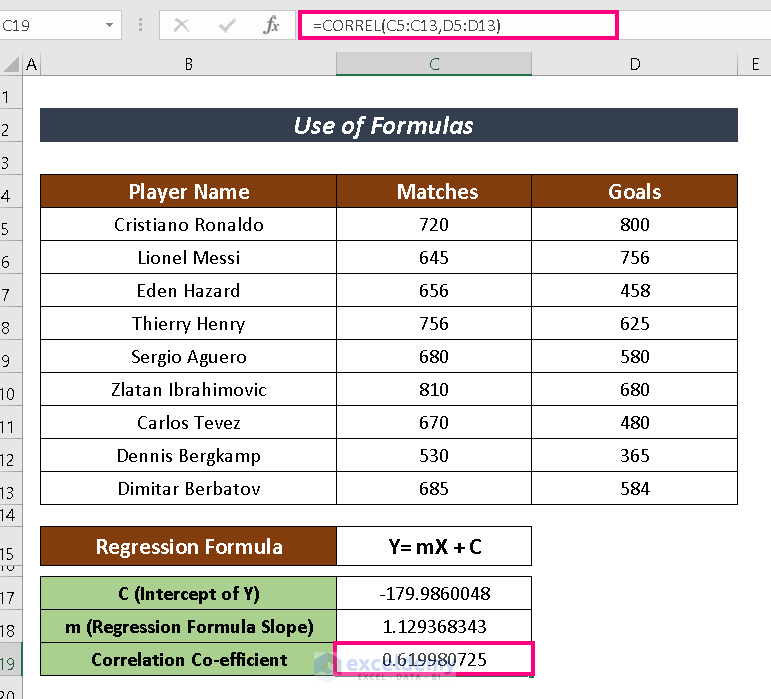
We are going to depict how strongly those two variables are connected with the CORREL Function.
- Write down the following formula to have the CORREL Function:
=CORREL(C5:C13,D5:D13)
- Now, click on ENTER to finish the process.
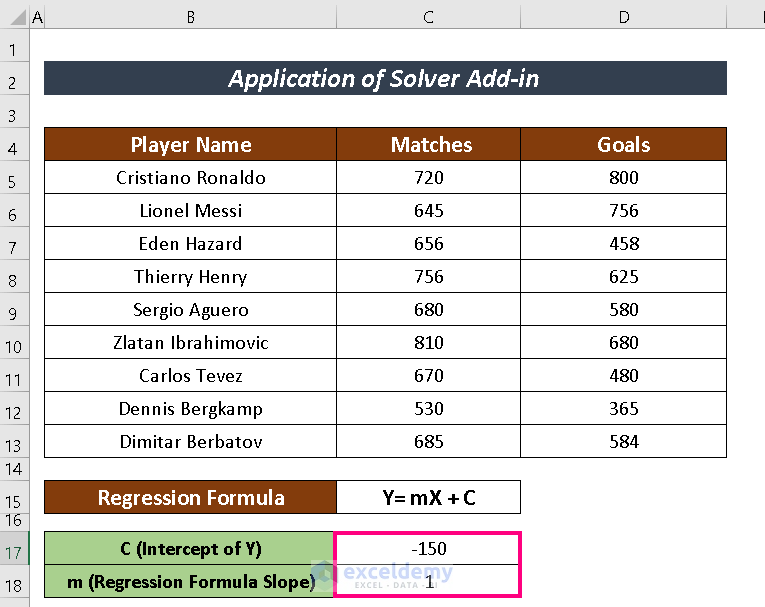
4. Linear Regression with Solver Add-in
Using Solver Add-in to do Linear Regression is complex compared to the previous procedures. This method includes some pre-calculation approach before conducting Solver Add-in. The pre-calculation includes:
- Assumption of values for the slope (m) and intercept (C) components.
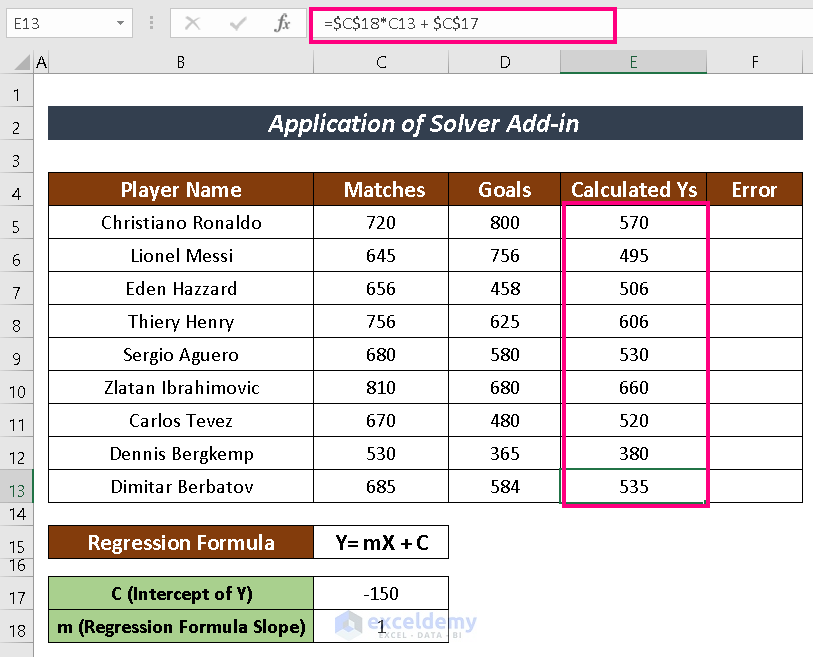
- Calculation of Ys using those assumed values.
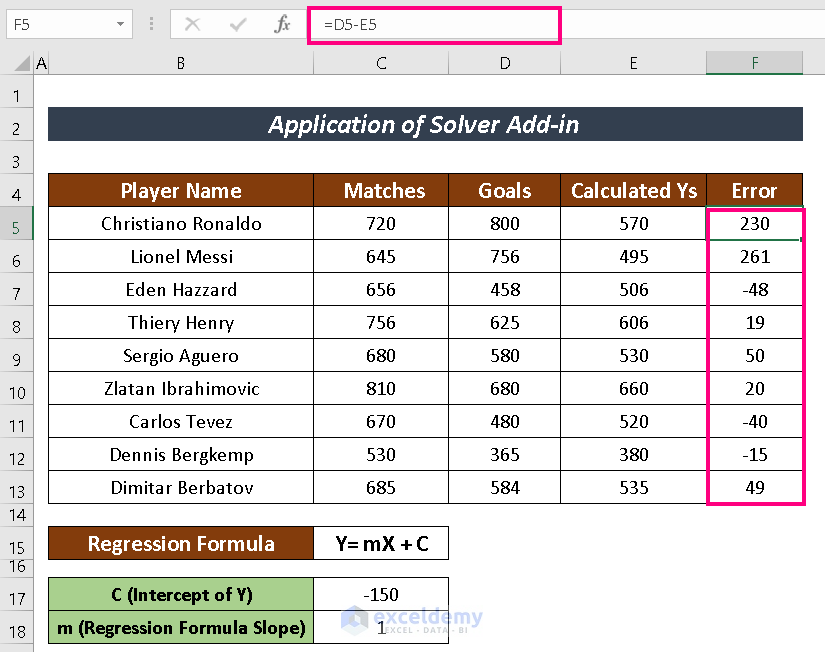
- Error finding between the newly calculated Ys and Y
- Use the Solver Add-in to minimize the error.
Steps:
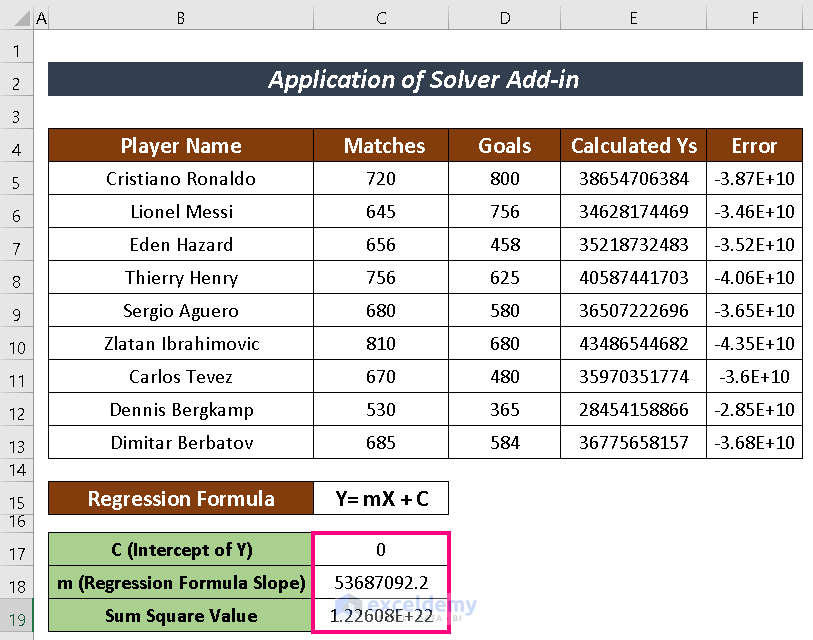
- Input the assumed value as Intercept of Y (e. -150) and Slope (i.e. 1).
- Calculate the value of Ys using the regression formula with the assumed value. The formula used here is:
=$C$18*C5 + $C$17
- Find the Error by subtracting the calculated Ys from the actual Ys.
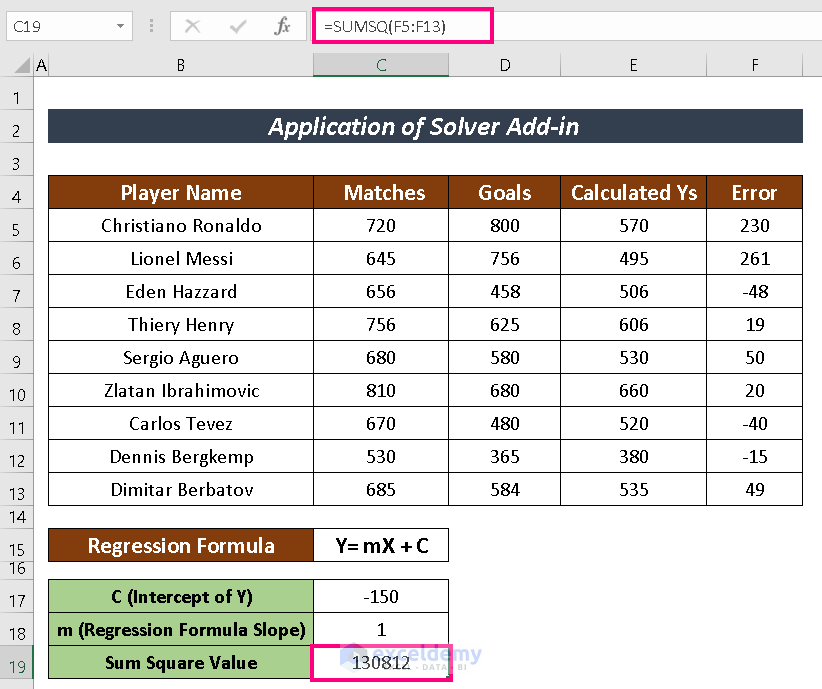
- Now, find the Sum Square value using the SUMSQ Function.
=SUMSQ(F5:F13)
Now, open the Add-ins box using the previously mentioned process and check the box Solver Add-in.
- Go to Data —> Solver.
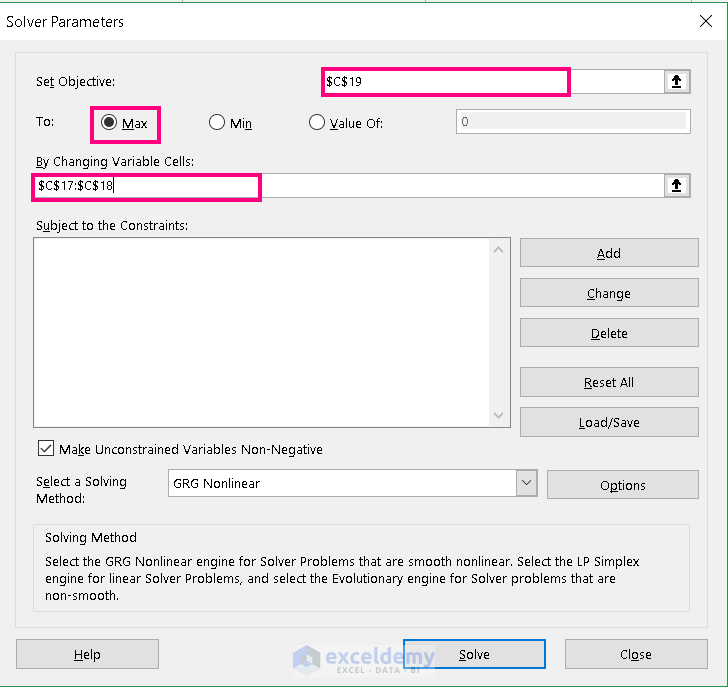
- From the Solver Parameters box, input Set Objective (i.e. C19).
- Check the box Max/Min/Value of depending on the dataset.
- Input Slope and Intercept cell numbers in the By Changing Variable Cells.
- Finally, press on Solve.
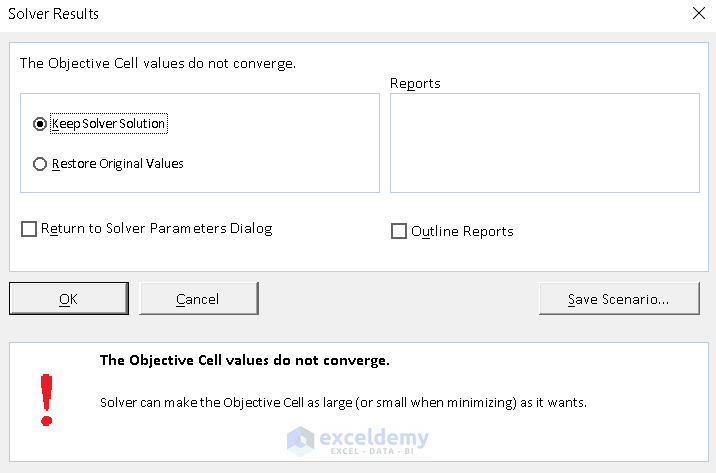
- Now, check the Keep Solver Solution and press OK.
The outcome includes estimated Y with the Linear Regression Analysis.
Read More: How to Interpret Linear Regression Results in Excel (with Easy Steps)
Practice Section
For further expertise, you can practice here.
Conclusion
I have tried to articulate 4 simple ways to do Linear Regression in Excel. I hope it will be helpful for Excel users. For any more questions, comment below.
