Method 1 – Using LOG Function in Excel with Default Base Argument (Log10)
Apply the LOG function without specifying the base argument; then it is assumed to be 10 by default.
The following formula in cell D5 will return a 10-based log value of the number in cell B5.
=LOG(B5)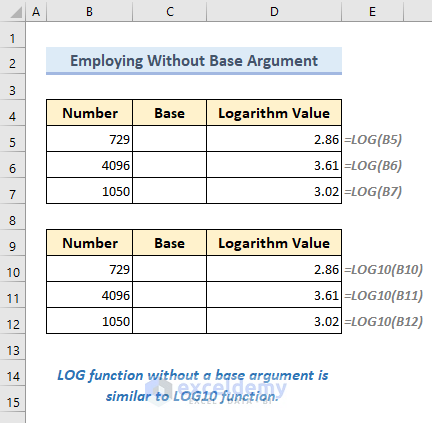
Note:
In Cell D10, we can attain the same results by applying the LOG10 function also as it returns 10-based logarithm values.
=LOG10(B10)Method 2 – Using LOG Function with a Custom Base
If we apply the LOG function with both number and base arguments, it returns the exponent to which the base argument must be raised to produce the number argument.
We have calculated the Log Values of some numbers in the following image. The bases are specified beside the numbers. Insert the following formula in cell D5, and copy this formula to the remaining cells of Column D by using the Fill Handle icon.
=LOG(B5,C5)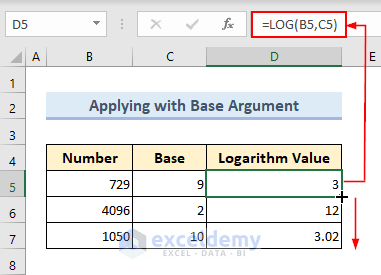
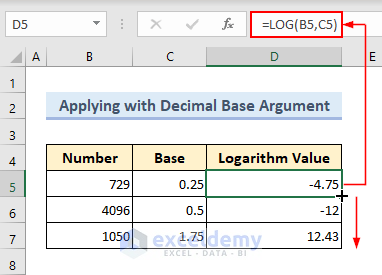
Method 3 – Applying a Decimal Base with LOG Function in Excel
The arguments of the LOG function can vary widely. For example, we can use decimal base arguments in the LOG function.
Method 4 – Combining Excel LOG and EXP Functions to Calculate the Natural Logarithm of a Number
Calculating natural logarithms requires the irrational number “e” as the base argument. This can be accomplished by combining the EXP function with the LOG function.
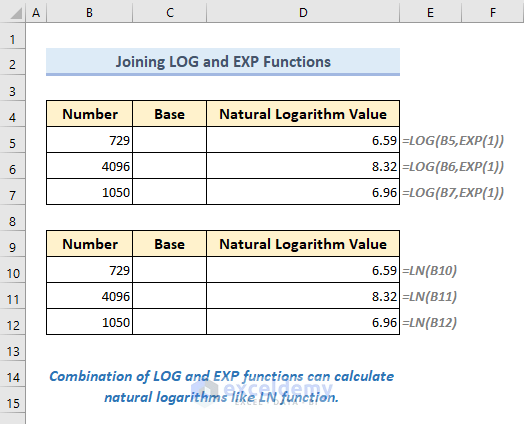
In Cell D5, insert the following formula and get the required output by pressing the Enter key.
=LOG(B5,EXP(1))The EXP function returns the exponential of 1 i.e. the irrational number “e”, which works as the base for the LOG function. Next, the LOG function returns the natural logarithm of the provided number.
Note:
We can apply the LN function as a better alternative to this formula. The formula to return the natural logarithm of a number by using the LN functions is given below:
=LN(B10)Method 5 – Applying Excel Log Function in VBA
Implement the LOG function in Excel VBA to calculate the logarithm of a given number with a specified base. In the following dataset, we have a number and a base value stored in Cells B5 and C5.
- To calculate the logarithm of these values, first, we have to go to the Developer tab and select the Visual Basic.
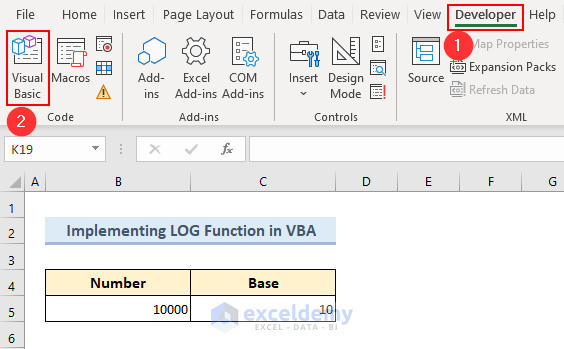
- If the Developer tab is not installed in your Excel, you can install it from File > Options > Customize Ribbon > Main Tabs directory.
- Open the window for inserting VBA code to use the keyboard shortcut ALT + F11.
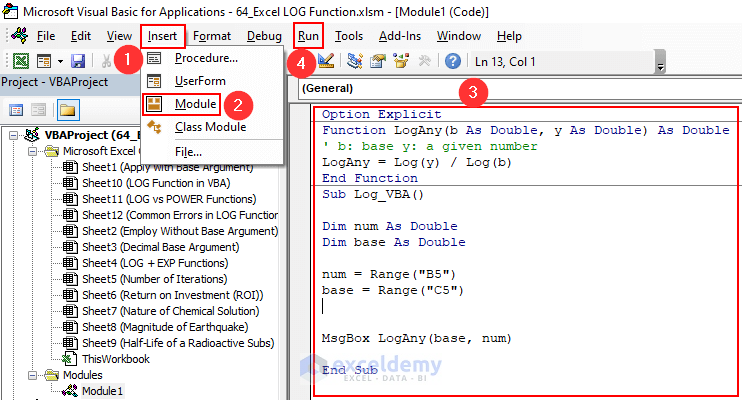
- The Microsoft Visual Basic for Applications window opens, from the Insert ribbon, select the Module option and then insert the following code.
Option Explicit
Function LogAny(b As Double, y As Double) As Double
' b: base y: a given number
LogAny = Log(y) / Log(b)
End Function
Sub Log_VBA()
Dim num As Double
Dim base As Double
num = Range("B5")
base = Range("C5")
MsgBox LogAny(base, num)
End Sub- Save and Run the module.
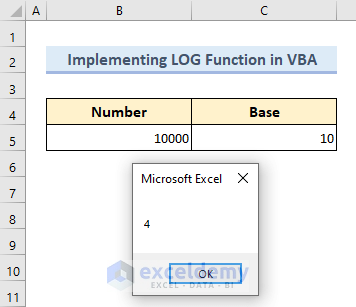
- A message box like the following will appear where we can see the required output.
LOG Function in Excel: 5 Real-Life Applications
Method 1 – Use LOG Function to Calculate the Number of Iterations Required to Find a Number (Binary Search)
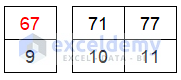
Consider the following sorted array of 12 numbers:

Suppose we want to search for the number 67 from the array.
- The number of iterations required to find this number by using the binary search method is-
Iteration-1:

Iteration-2:

Iteration-3:
- These number of iterations could have been calculated by using a simple Excel formula-
=ROUND(LOG(12,2),0)- This formula simply returns how many times we have to divide the array into halves.
- Let’s have a look at the following dataset where we have item counts for a list of arrays.
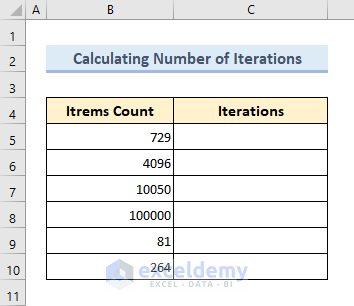
- To calculate the number of iterations required to find any item from these arrays by using a combination of the LOG and ROUND functions.
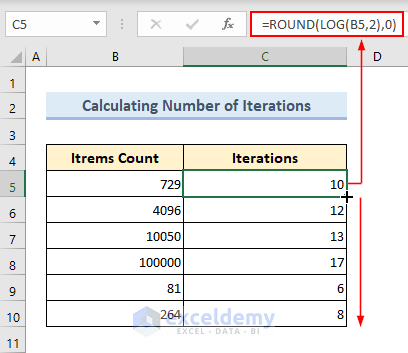
- Type in the following formula in Cell C5 and press Enter key to get the required result.
=ROUND(LOG(B5,2),0)- Use the Fill Handle tool to copy the formula in other cells of Column C.
Formula Explanation:
- LOG(B5,2)
The LOG function returns the 2-base logarithm of the specified items count value.
- ROUND(LOG(B5,2),0)
If the LOG function returns a decimal number, then the ROUND function rounds the number to 0 decimal digits.
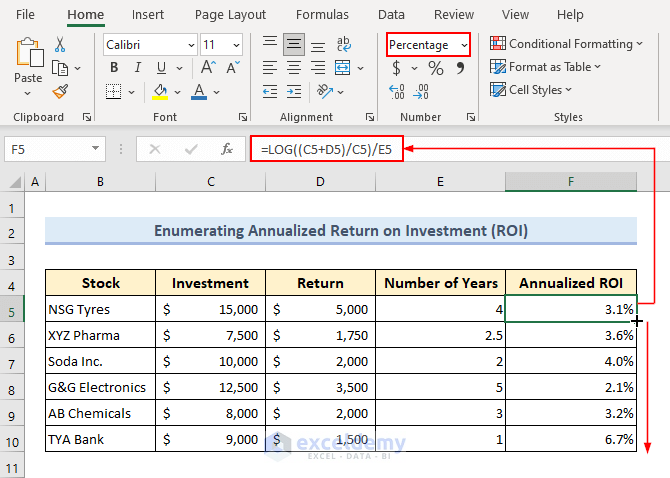
Method 2 – Apply LOG Function in Evaluation of Annualized Return on Investment (ROI) for Continuous Compounding
Return on Investment (ROI) is a financial parameter that enumerates the profitability of an investment relative to its cost.
The annualized ROI value under continuous compounding can be described as below-
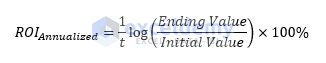
The Initial Value represents the Investment made on any stock and the Ending Value represents the summation of the Investment made and the value returned from the investment after t years.
The following dataset where we have investment, return, and number of years to get the return listed for several stocks.
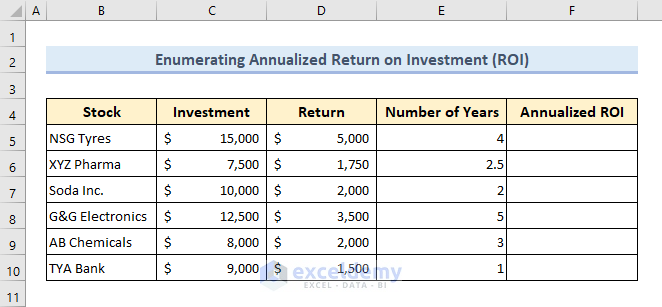
To enumerate the annualized ROI value for each stock so that we can find potential stocks for investment.
- Insert the following formula in Cell F5 and press the Enter key.
=LOG((C5+D5)/C5)/E5- Drag the Fill Handle icon down to copy the formula in the remaining cells of Column F.
Method 3 – Find the Nature of Chemical Solutions Using IF, LOG and POWER Functions
The nature of any chemical solution can be determined from its PH value and the PH values can be calculated using the LOG function in Excel.
If the PH < 7, then the solution is of acidic nature, if the PH > 7, then the solution is of alkaline nature, and if PH = 7, then the solution is of neutral nature.
We have the concentration of Hydrogen ions for a list of chemical solutions. We want to calculate the PH value and nature of these solutions.
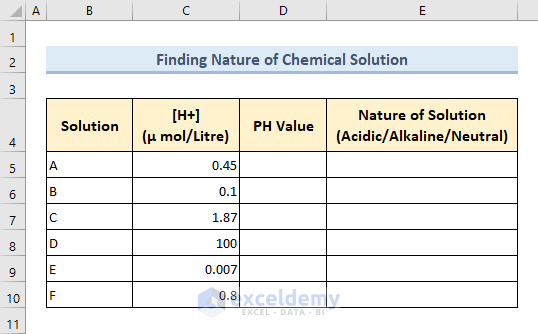
Since the concentration values are provided in μmol/Litre units, we have to multiply these concentration values by 10-6 while calculating PH values. We require the POWER function along with the LOG function for this purpose.
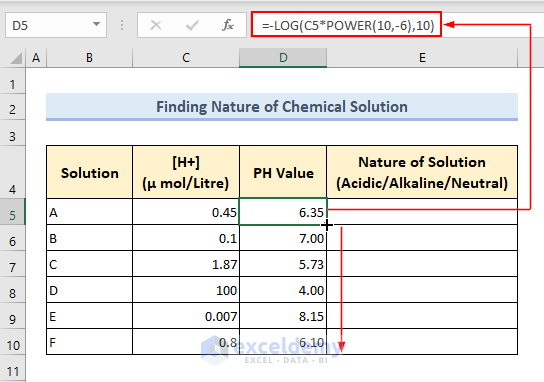
- To calculate the PH values of the solutions, first, type in the following formula in Cell D5 and press Enter key.
=-LOG(C5*POWER(10,-6),10)- Use the Fill Handle tool to copy the formula in other cells of Column D.
Formula Explanation:
- POWER(10,-6)
The POWER function here is used for returning the value 10-6 (10 raised to the power -6).
- -LOG(C5*POWER(10,-6),10)
This formula returns the negative 10-based logarithm of the Hydrogen ion concentration values i.e. PH values.
- Determine the nature of the solutions based on these PH values.
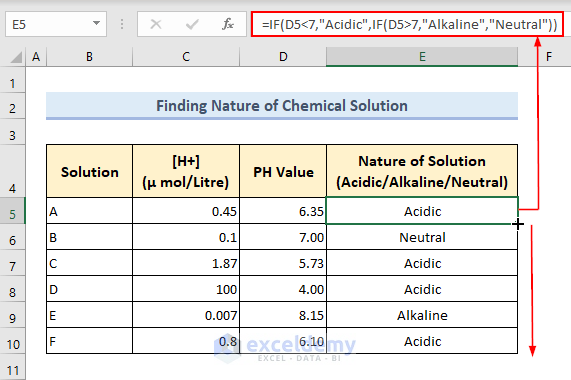
- Type the formula below in Cell E5 and press Enter key to get the required nature of the solution. Then copy this formula down.
=IF(D5<7,"Acidic",IF(D5>7,"Alkaline","Neutral"))Formula Explanation:
- The first IF function checks whether the PH value is less than 7. If the criterion is true, then it returns “Acidic”.
- The second IF function is executed, which checks whether the PH value is greater than 7. If this criterion is true, then the second IF function returns “Alkaline”. It returns “Neutral”.
Method 4 – Measuring the Magnitude of Earthquakes with LOG Function
The magnitude of an earthquake is a measure of the size or strength of the earthquake. This measure is an important factor in assessing the potential impact and damage of an earthquake. There are several different scales used to measure earthquake magnitude. Here, we’ll use the formula below which is provided by Seismologist Dr. Hiroo Kanamori.
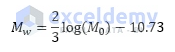
M0 is the Seismic Moment and Mw is the Moment Magnitude of any earthquake.
To calculate the magnitude of earthquakes, we’ll use the following dataset, which lists the Seismic Moments of several earthquakes in column C.
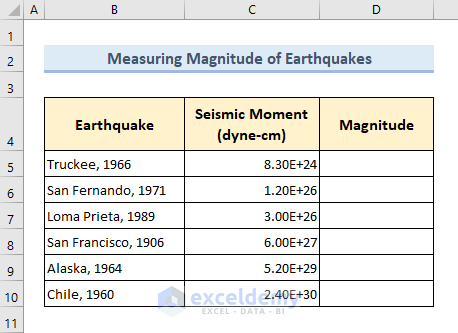
The values of Seismic Moments are measured in dyne-cm units and categorized in Scientific format. Now, let’s calculate the magnitude of the listed earthquakes.
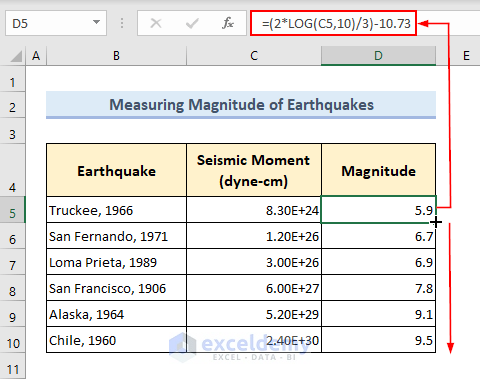
- In Cell D5, type in the following formula and press Enter key to get the required output.
=(2*LOG(C5,10)/3)-10.73- Drag the Fill Handle icon to copy the formula for the remaining earthquakes.
Method 5 – Using LOG Function to Calculate the Half-Life of Radioactive Substances
The half-life of a radioactive substance is the amount of time it takes for half of the original radioactive atoms to decay. This is an important parameter for understanding the behavior and properties of radioactive materials.
This parameter is widely used in the Nuclear Power Sector, Medical science, Geology, etc. fields. To calculate this parameter, we first have to calculate the decay constant (k) by utilizing the variables initial amount (N0), remaining amount (N), and decay period (t).
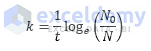
After calculating the decay constant, we can enumerate half-life (T1/2) by using the formula below-
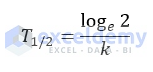
We have got the initial amount (Column C), the remaining amount (Column D), and the decay period (Column E) for several elements listed here.
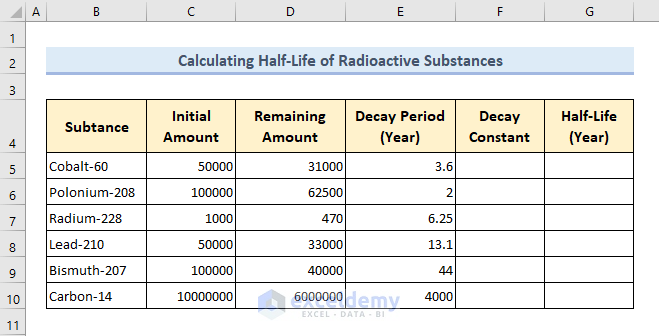
Calculate the half-lives for these radioactive elements.
- Insert the following formula in Cell F5 and press Enter key to calculate the decay constant.
=LOG(C5/D5,EXP(1))/E5- Drag the Fill Handle icon down to copy the formula in other cells of Column F.
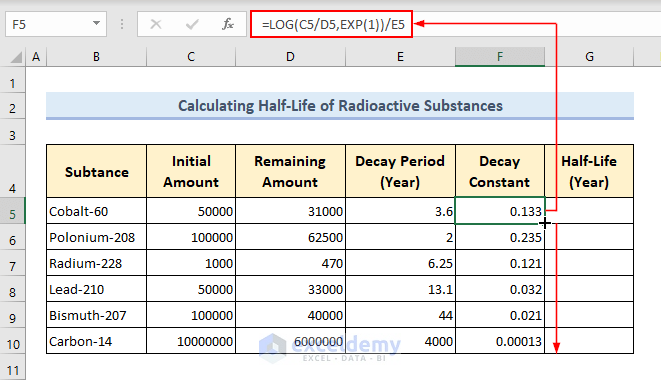
Formula Explanation:
- EXP(1)
The EXP function returns the exponential of 1 i.e. the irrational number “e”, which works as the base for the LOG function.
- LOG(C5/D5,EXP(1))/E5
This formula calculates the natural logarithm of the ratio of the initial amount and the remaining amount of the radioactive substance and divides it by the decay period to calculate the decay constant.
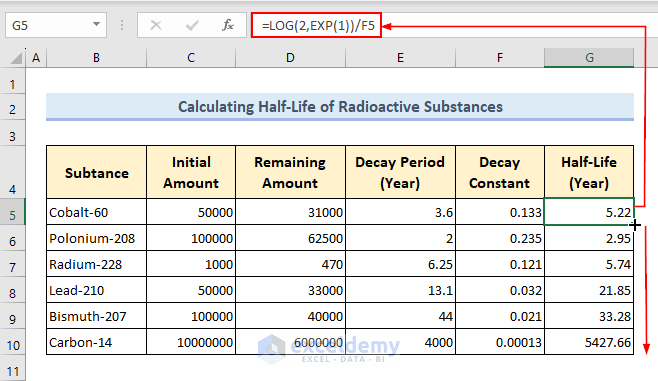
- Get the half-life value by inserting the formula in Cell G5 and pressing the Enter key.
=LOG(2,EXP(1))/F5- Use the Fill Handle tool to copy this formula for the remaining radioactive substances.
Common Errors with Excel LOG Function
The execution of the Excel LOG function may seem simple, but some common errors can occur if the users provide wrong arguments. Three different types of errors can occur for providing irrelevant arguments.
- Negative or Zero Arguments Return #NUM! Error
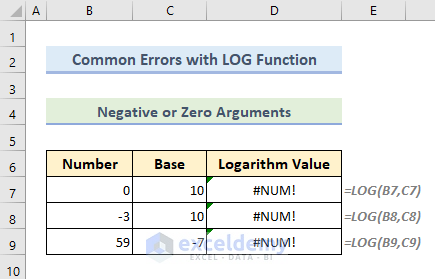
The number and base arguments in the LOG function must be greater than zero. If a negative or zero value is used for any argument, the LOG function returns a #NUM! error.
- Non-Numeric Arguments Cause #VALUE! Error
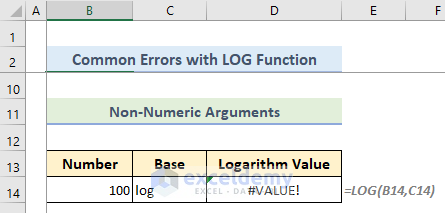
The arguments of the LOG function can’t be text values, either. If a text value is used for any argument, then the LOG function returns #VALUE! error.
- #DIV/0! Error Occurs If Base Argument Value Is Equal to 1
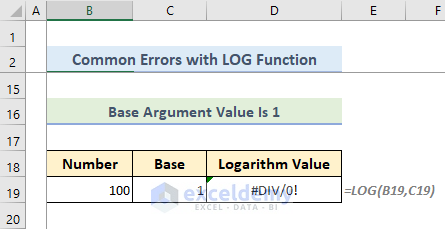
The base argument value can’t be equal to 1. If we set the base argument to 1, then the LOG function will return #DIV/0! Error.
Excel LOG vs POWER Function: What Is the Difference?
The LOG function is the reverse of the POWER function. The POWER function is used to raise a number to a given exponent, the LOG function can be used to return the same exponent.

- Apply the following formula using the POWER function to raise the base to the given exponent.
=POWER(B5, C5)- Use the output of the POWER function as the number argument for the LOG function, we can return the exponent value. The formula is given below for this operation-
=LOG(D5,B5)Things to Remember
- If the base argument is omitted while applying the LOG function, then it is assumed to be 10.
- The arguments of the LOG function can’t be negative, zero, or non-numeric.
- The base argument of the LOG function can’t be equal to 1.
Frequently Asked Questions
1. Can the LOG function be used to calculate the natural logarithm?
Answer: Yes, the LOG function can calculate natural logarithms. The base argument has to be set to the irrational number “e” for this. We can apply the following formula to calculate the natural logarithms of any number.
=LOG(number, EXP(1))
Provide the number for which you want the natural logarithm value.
2. What is the difference between the LOG, LOG10, and LN functions in Excel?
Answer: The syntax and purpose of using the LOG, LOG10, and LN functions are listed below-
| Function | Syntax | Output |
|---|---|---|
| LOG | LOG(number, [base]) | The logarithm of a number based on the specified base |
| LOG10 | LOG10(number) | 10-base logarithm values |
| LN | LN(number) | e-base logarithm values |
The main difference between these three functions is the base of the logarithm that they use. The LN function calculates the natural logarithm (base e), the LOG10 function calculates the logarithm to base 10, and the LOG function allows us to specify the base value.
3. How do I troubleshoot errors that occur when using the LOG function in Excel?
Answer: Here are some tips for troubleshooting errors in formulas that may occur when using the LOG function in Excel:
- Check your syntax: Make sure that you have entered the correct syntax for the LOG Make sure that the syntax is correct and that there are no missing or extra parentheses, commas, or other syntax errors.
- Check your arguments: Make sure that the arguments you have provided to the LOG function are valid.
- Check for errors in the source data.
- Check your settings: Check your Excel options and make sure that the calculation settings are set to automatic.
By following these tips, you should be able to troubleshoot most errors that occur when using the LOG function in Excel.
Download Practice Workbook
You may download the following file and practice yourself.
Excel LOG Function: Knowledge Hub
<< Go Back to Excel Functions | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!


