How to Calculate Alpha and Beta in Excel (Easy Steps)

Overview of Alpha and Beta in the Stock Market

Alpha and Beta are two important measures used in finance to evaluate the performance of an investment compared to its standard.

Alpha is a measure of an investment’s performance that cannot be attributed to the performance of the market as a whole. A positive alpha indicates that the investment has performed better than its standard, while a negative alpha indicates that the investment has underperformed.

Beta measures how much an investment’s returns move in response to changes in the standard returns. A beta of 1 indicates that an investment’s returns move in line with the standard returns, while a beta greater than 1 indicates that the investment is more volatile than the standard, and a beta less than 1 indicates that the investment is less volatile than the standard.

Formula for Calculating Alpha:

Alpha= Average portfolio return of the investment – (Risk-free rate + Beta * (Average market returns of the benchmark – Risk-free rate))

Formula for Calculating Beta:

Beta= Covariance of the portfolio returns with the expected returns / Variance of the portfolio returns

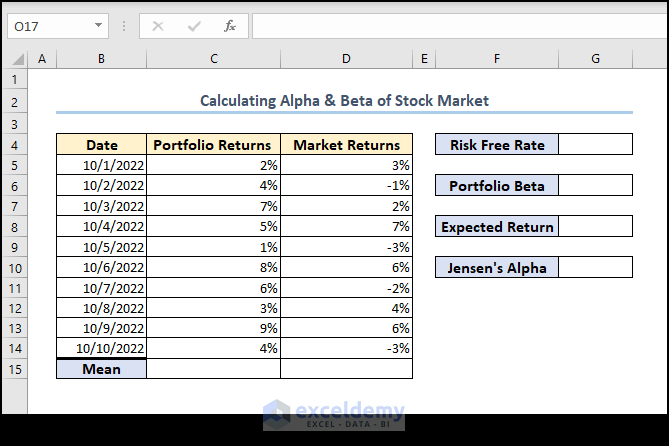
Step 1 – Prepare Outline and Dataset

Create a dataset containing Portfolio Returns (standard returns) and Market Returns.

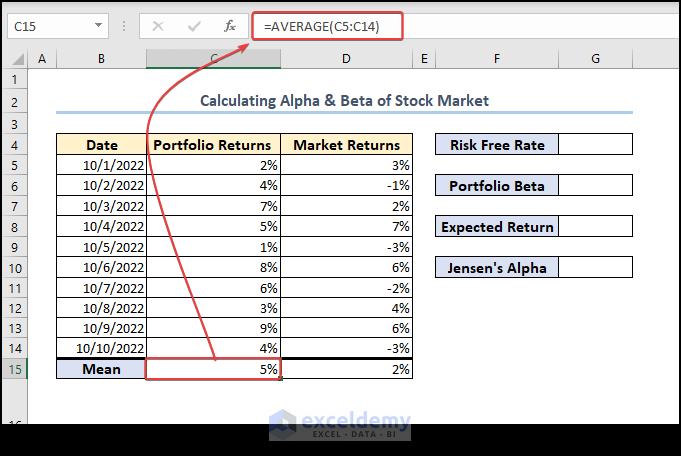
Use the AVERAGE function in Excel to find the average of Portfolio Returns:

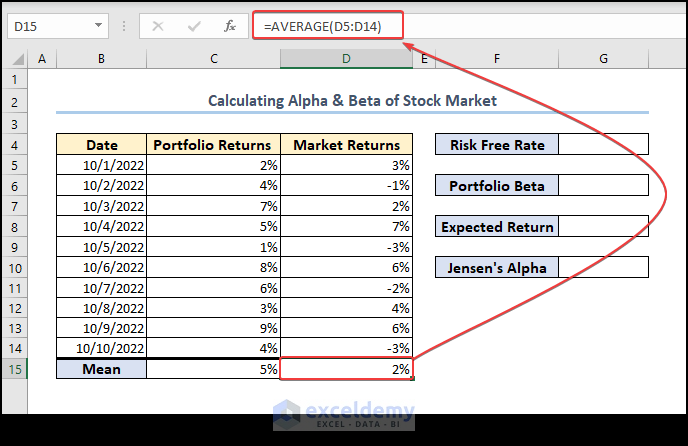
=AVERAGE(C5:C14)

Similarly, calculate the average of Market Returns:

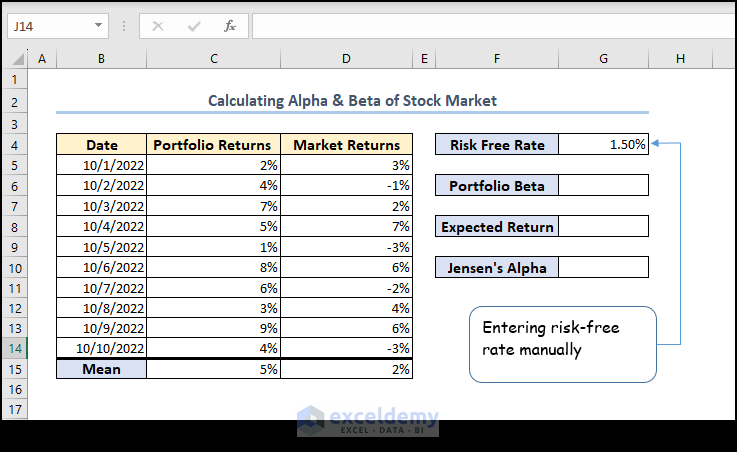
=AVERAGE(D5:D14)

Step 2 – Define a Risk-Free Rate

Manually insert the Risk-Free Rate. Let’s assume a risk-free rate of 1.5%.

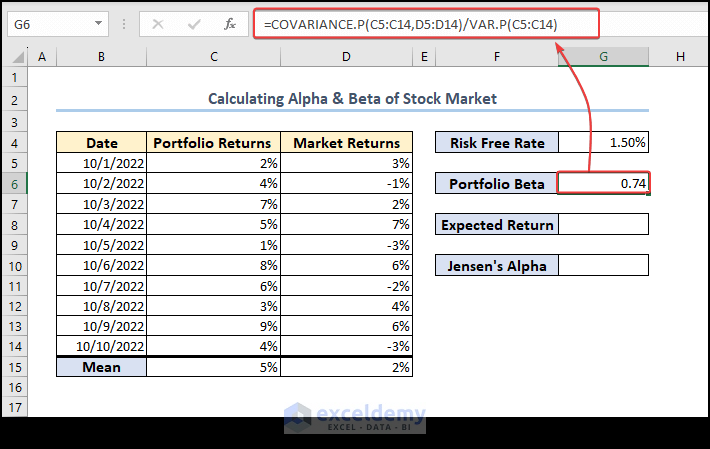
Step 3 – Calculate Beta Using COVARIANCE.P and VAR.P Functions

Calculate Beta using the following formula in cell G6:

=COVARIANCE.P(C5:C14,D5:D14)/VAR.P(C5:C14)

Explanation: The COVARIANCE.P function computes the covariance between the two data sets (Portfolio Returns (C5:C14) and Market Returns (C5:C14 )), and VAR.P calculates the variance of Portfolio Returns. We divided the covariance result with the variance result to get Beta.

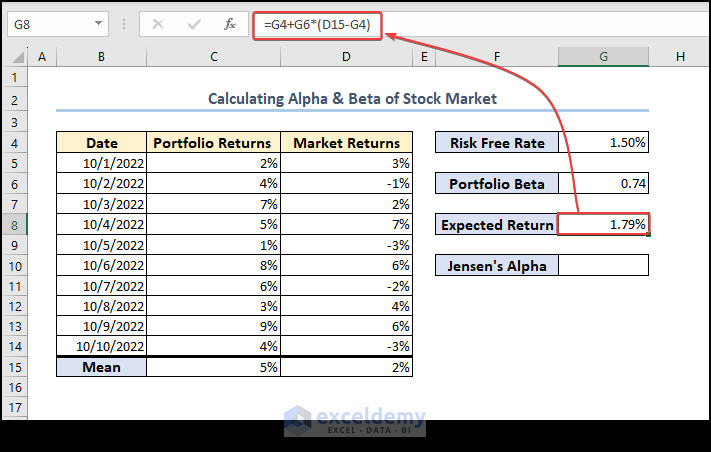
Step 4 – Determine Expected Return

Calculate the Expected Return using the following formula in cell G8:

=G4+G6*(D15-G4)

Explanation: Expected Return = (Risk-free rate + Beta * (Average market returns of the benchmark – Risk-free rate))

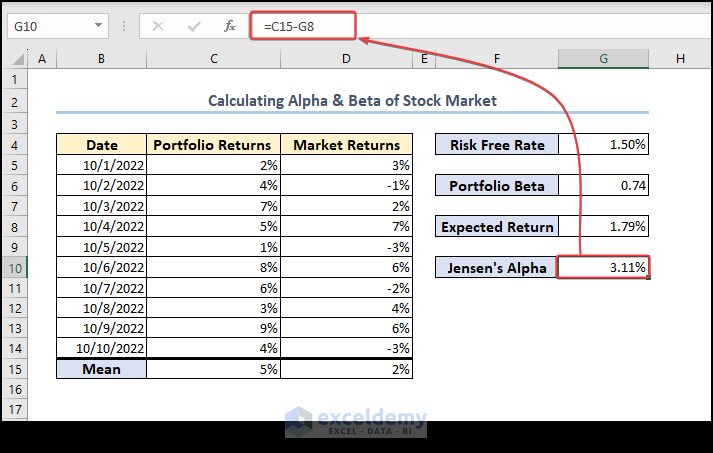
Step 5 – Calculate Jensen’s Alpha

Compute Alpha using the following formula in cell G10:

=C15-G8

Explanation: Alpha = Average portfolio return of the investment – Expected Return

Frequently Asked Questions

Interpreting Alpha and Beta:
- A positive alpha means the investment outperformed its standard, while a negative alpha indicates underperformance.
- Beta of 1 implies returns move in line with the standard, >1 means higher volatility, and <1 means lower volatility.

Calculating Daily Returns:
- Use the formula: (Price today - Price yesterday) / Price yesterday.

Limitations of Alpha and Beta:
- Historical data-based; may not predict future performance.
- Ignores management quality, industry trends, and macroeconomic conditions.
- Not suitable for all investment types.

Remember

To handle cell references carefully (consider absolute references with “$” sign).
Adjust the Risk-Free Rate as needed.