How to Use Excel Evolutionary Solver (With Easy Steps)

In this tutorial, I am going to show you how to use the Evolutionary solver in Excel to solve complex optimization problems. You can use this solver in numerous real-life cases where other Excel Solvers may not be applicable. Also, throughout this tutorial, you will learn some important topics like scatter charts, various functions, etc.

How to Use Evolutionary Solver in Excel: Step-by-Step Procedures

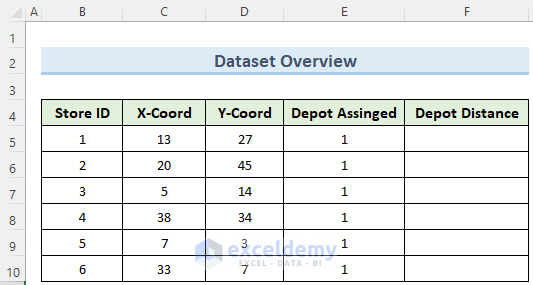
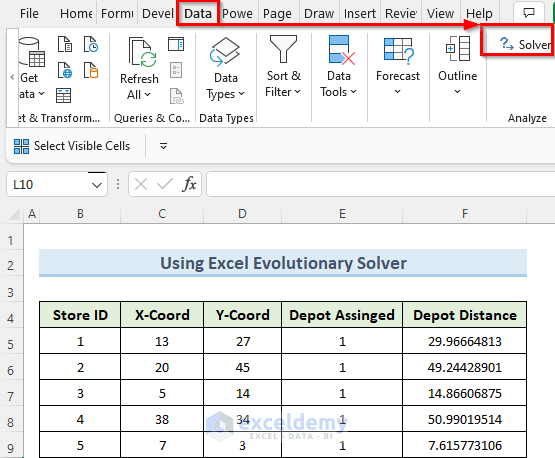
We have taken a concise dataset to explain the steps of this tutorial. This dataset has 6 rows and approximately 11 columns. Here we want to distribute the depots in a way so that the Total Distance becomes minimum.

Step 1: Creating Data Tables

In this first step, we will insert the data in a table format which the Excel Evolutionary solver will need to perform calculations.

• First, insert the data of columns Store ID, X-Coord, Y-Coord, and Depot Assigned manually from the keyboard.
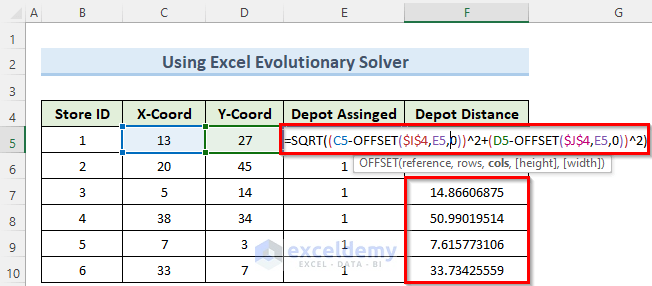
• Then, click on cell F5 and enter the following formula:

• Next, copy this formula to all the cells below using Fill Handle which will give the Depot Distances for all the stores.

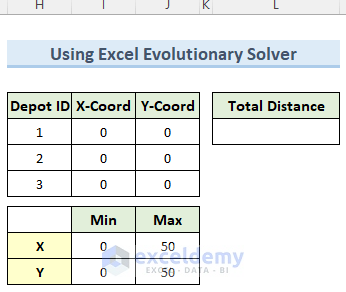
• Now, insert the data in the other tables as shown in the image below.

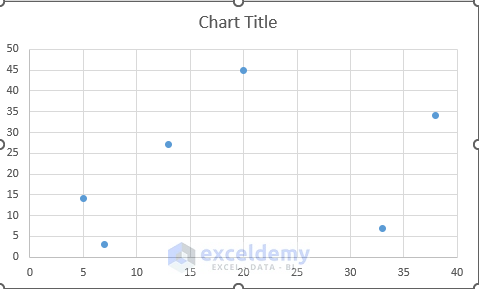
Step 2: Generating Scatter Plot

To get a visual idea of the locations of the stores, we will plot them on an Excel scatter chart. Follow the steps below to do this.

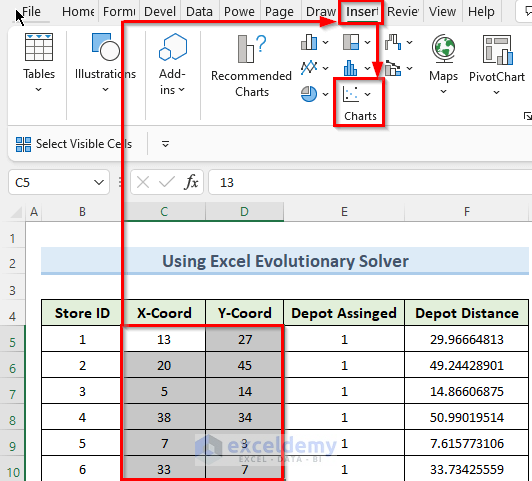
• To begin this step, select the cells from C5 to D10.
• Now, navigate to the Insert tab and select Scatter Chart.

• As a result, this will generate a 2D Scatter Plot showing the relative position of the stores.

Read More: Where Is Solver in Excel

Step 3: Setting Up Solver

We need to set up the solver to perform the calculations properly. Here, we will set the objective cell, the changing cells, and all the other constraints.

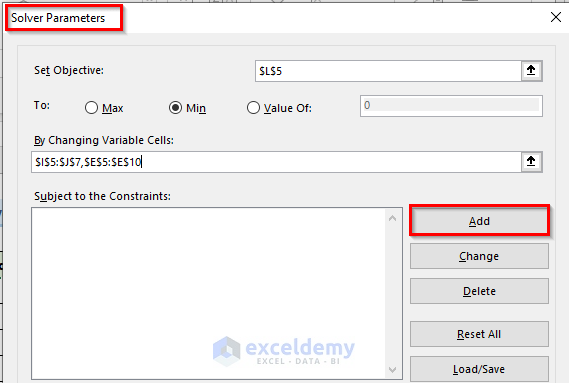
• For this, go to the Data tab and click on Solver.

• Immediately, the Solver Parameters window will now open.
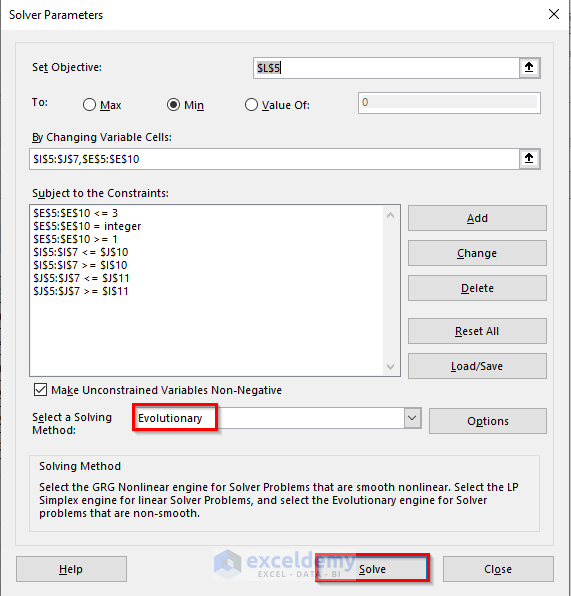
• Next, insert the Set Objective, To, and By Changing Variable Cells fields as in the image below.
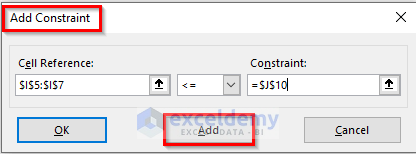
• Now, to add necessary constraints, click on Add.

• Here, in the new Add Constraint window, fill the 3 required fields and click Add after entering a constraint.
• Then, once you have entered all the constraints, click OK.

Read More: How to Use Solver in Excel 

Step 4: Finding Solution

Once we have set up all the parameters, now we are ready to perform the calculations. We will choose the Evolutionary method to solve this problem.

• Now, you can see that we have entered all the necessary 7 constraints as below.
• Then, set Evolutionary as the Solving Method and click Solve.

• Consequently, this will give you the required solution and show the window below.

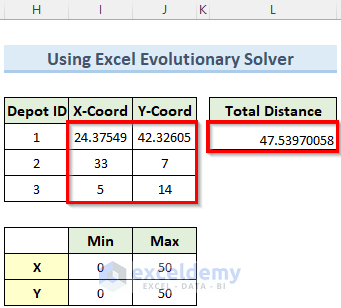
• So, as you can see, the solver calculated the Total Distance and coordinates of the Depots.

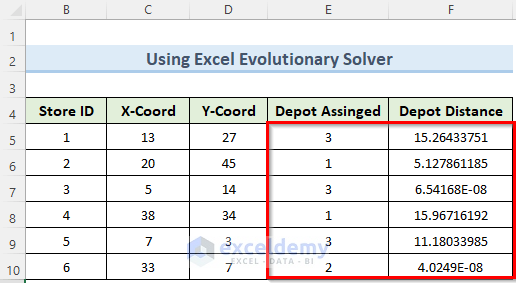
• Similarly, the solver should calculate the data of the first table as well.

Comparing Evolutionary and GRG Nonlinear Solvers in Excel

The GRG Nonlinear solver in Excel works by trying to find a point at which the slope of the function is zero. This is to make sure that the function reaches either a maximum or a minimum value at that point. But if there are any non-smooth functions in the target cell like MAX, MIN, SUMIF, COUNTIF, etc, then for them we can’t use the GRG Nonlinear solver.

On the other hand, the Evolutionary solver doesn’t rely on finding slope. So it can not determine whether a given solution is optimal or not. It only knows that a new candidate solution is better than previous ones. So it stops calculation when a certain set criterion is achieved.

Download Practice Workbook

You can download the practice workbook from here.

Conclusion

I hope that you were able to apply the above steps to solve a problem using the Evolutionary solver in Excel. Although we have used a relatively simple problem for this tutorial, you can use these steps to solve more complex real-life problems as well. If you get stuck at any steps, I recommend going through the steps a few times to clear up any confusion.

<< Go Back to Solver in Excel | Learn Excel