Correlation and the correlation coefficient are often discussed in many financial sectors such as the stock market and investment portfolio analysis. This mainly determines the relationship between two variables. In this article, I will discuss correlation and show you 3 simple ways to find a correlation between two variables in Excel.
What Is Correlation?
Correlation is a statistical measure that indicates whether there is a relationship between two variables. Correlation measures the strength of the relationship between two variables, as well as whether or not there is a positive or negative relationship between the two variables.
The discussion of correlation is prevalent in many financial sectors. Financial papers and analysts often evaluate the correlation between the price of gold and let’s say a certain stock.
A positive correlation basically means that as one variable increases, so does the other, whereas a negative correlation refers to a situation where one variable increases, and the other decreases. This is mainly determined by the correlation coefficient value.
Correlation Coefficient Interpretation
The values for the correlation coefficient, r fall in the range of +1.0 to -1.0, depending on the strength of the relationship between the two variables.
- An r of 0 indicates that there is no relationship between the two variables.
- An r of +1.0 describes a perfect positive correlation between two variables whereas an r of -1.0 describes a perfect negative correlation.
Notes:
- There is one main issue to note with the correlation coefficient and that is that it should not be used to denote a cause and effect relationship. For example, smoking causes an increase in the risk of lung cancer, whereas smoking and alcoholism are correlated (one does not cause the other in this scenario).
- It is very important to note that there may be another variable affecting the relationship between two variables and therefore not use correlation as a causation indicator.
Find Correlation Between Two Variables in Excel: 3 Easy Ways
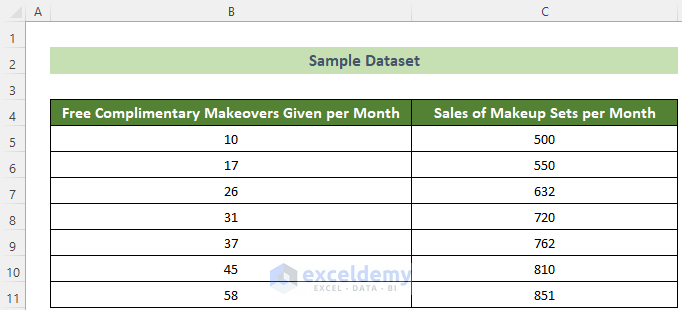
Say, a store manager working at a hypothetical department store is looking at the relationship between the monthly number of free complimentary makeovers given by the beauty department and the monthly sales of makeup sets in that specific department. The sample dataset is given below.
You can follow any of the 3 ways given below to find the correlation between these two variables in Excel.
1. Using the CORREL Function in Excel 2007 | 2010 | 2016 or More
The simplest way to find the correlation between two values is to use the CORREL function. Follow the steps below to do this.
📌 Steps:
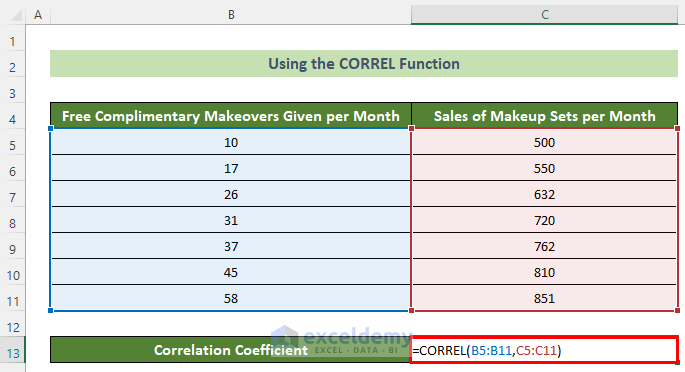
- First and foremost, click on the C13 cell and insert the following formula.
=CORREL(B5:B11,C5:C11)- Subsequently, press the Enter button.
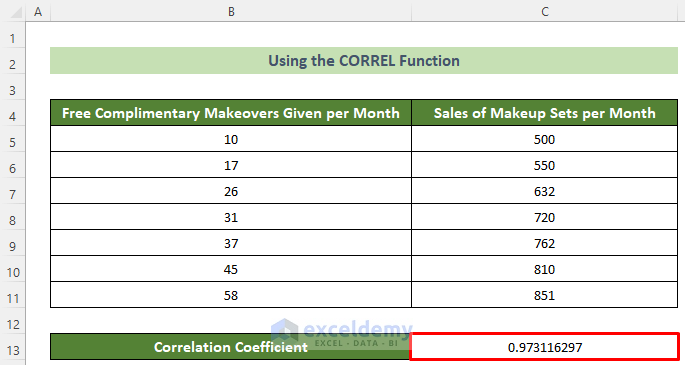
Thus, you will be able to calculate the correlation coefficient of the two selected variables dataset. And, thus you can say they are positively related to each other. For instance, the result sheet would look like this.
Read More: How to Make a Correlation Table in Excel
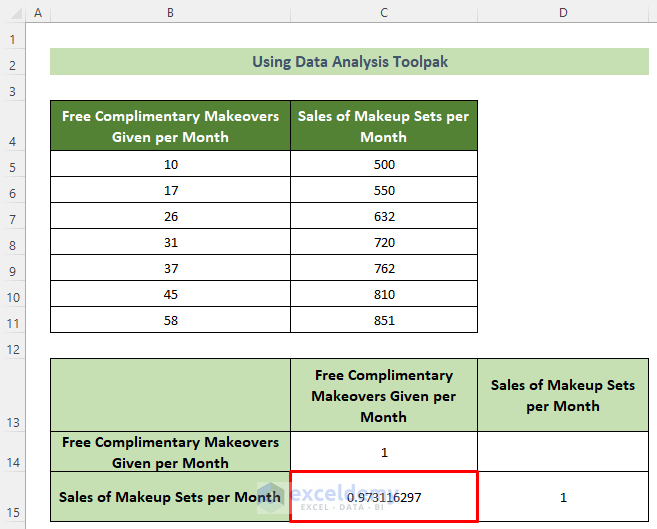
2. Use Data Analysis ToolPak to Find Correlation Between Two Variables
Another famous and frequent way to find correlation coefficients is to use the Excel Data Analysis ToolPak. Go through the steps below to achieve your target in this way.
📌 Steps:
- At the very beginning, go to the File tab from your Excel ribbon.
- Afterward, choose Options from the expanded File tab.
- As a result, the Excel Options window will appear.
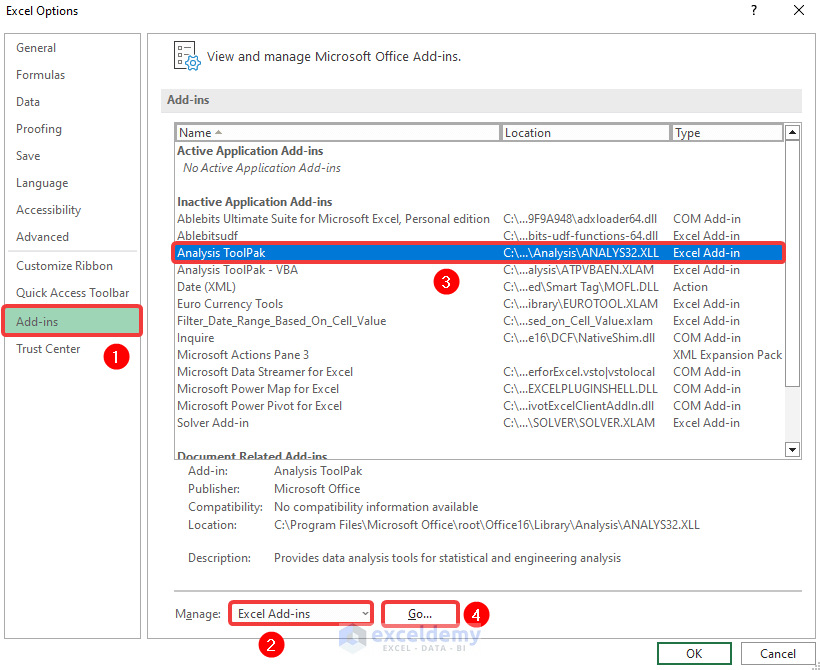
- Following, go to the Add-ins tab of this window >> choose Excel Add-ins at the Manage: options list >> choose the Analysis ToolPak from the Inactive Applications Add-ins list >> click on the Go… button.
- Consequently, the Add-ins window will appear.
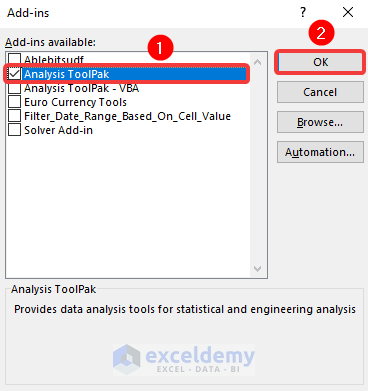
- Subsequently, choose the option Analysis ToolPak and click on the OK button.
- Thus, you will see there will be a new tool named Data Analysis in the Data tab.
- Now, go to the Data tab >> Data Analysis tool.
- As a result, the Data Analysis window will appear.
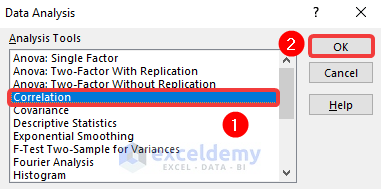
- Following, click on the Correlation option and click on the OK button.
- At this time, the Correlation window will appear.
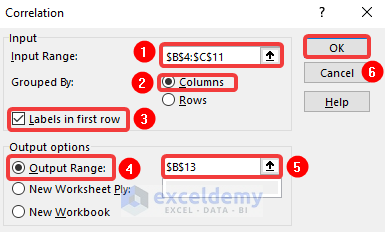
- Subsequently, choose the Input Range: as B4:C11 >> choose Columns option in the Grouped By: options >> tick on the Labels in first row option.
- Following, from the Output options group, put the radio button on the Output Range: option and refer to cell B13.
- Last but not least, click on the OK button.
As a result, the correlation matrix will appear on the B13 cell and you will get your desired correlation coefficient for these variables. And, the final outcome should look like this.
Read More: How to Calculate Cross Correlation in Excel
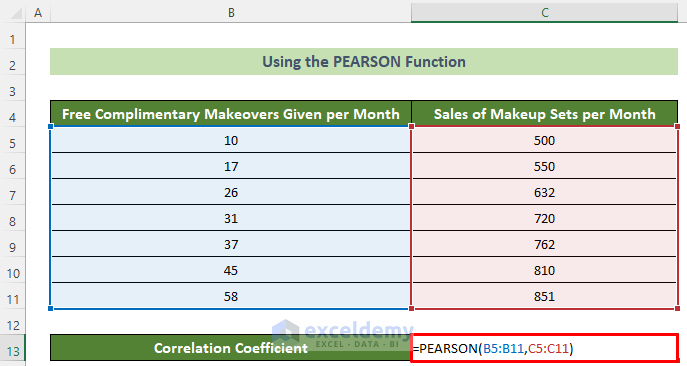
3. Use PEARSON Function in Excel to Find Correlation
Moreover, you can use the PEARSON function to calculate the correlation coefficient. Follow the steps below to accomplish this.
📌 Steps:
- First, click on the C13 cell and write the following formula.
=PEARSON(B5:B11,C5:C11)- Afterward, hit the Enter button.
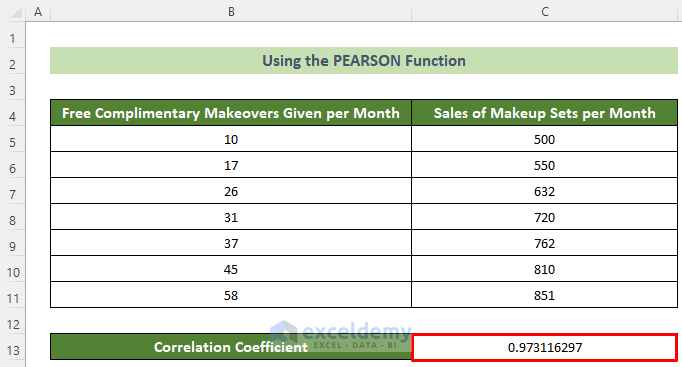
As a result, you will get the correlation coefficient for these two arrays and thus, you can find the correlation between two variables in Excel. For instance, the final output should look like this.
Read More: How to Calculate Autocorrelation in Excel
Calculate Correlation Coefficient in Excel Graph
Calculating and displaying correlation coefficients in Excel graphs is a frequent need for many of us. You can easily accomplish this by following the steps below.
📌 Steps:
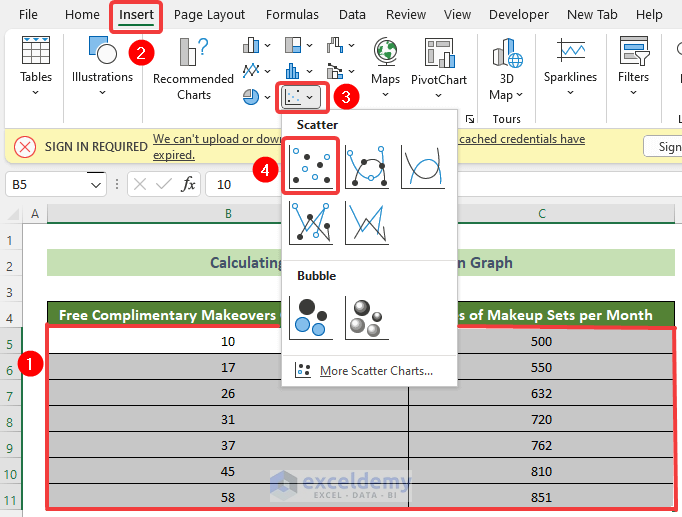
- First and foremost, select the variables’ dataset (B5:C11 here).
- Subsequently, go to the Insert tab >> Insert Scatter (X,Y) or Bubble Chart tool >> Scatter option.
- As a result, you will get the scatter chart for your selected dataset.
- For a cleaner and better look, click on the Chart Elements icon >> tick on the Axes option and the Trendline option.
- Afterward, click on the Chart Elements icon >> Rightward arrow beside the Trendline option >> More Options… option.
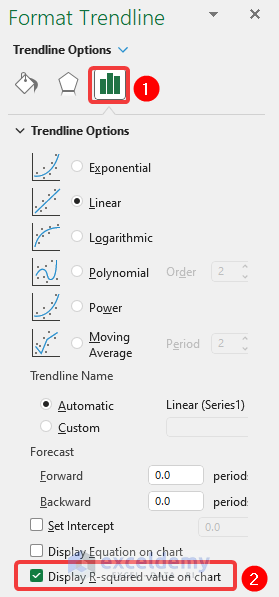
- As a result, the Format Trendline pane will appear on the right side of the Excel.
- Here, go to the Trendline Options group >> tick on the Display R-squared value on chart option.
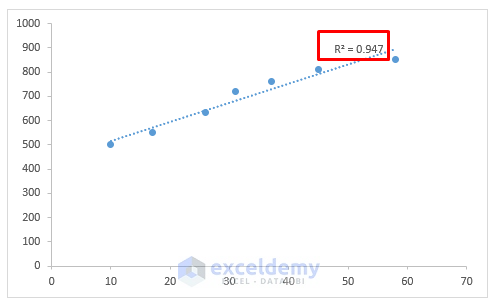
As a result, you will see that the R-squared value is shown inside the graph. This is the correlation coefficient squared value. So, the final output should look like this.
Read More: How to Make Correlation Graph in Excel
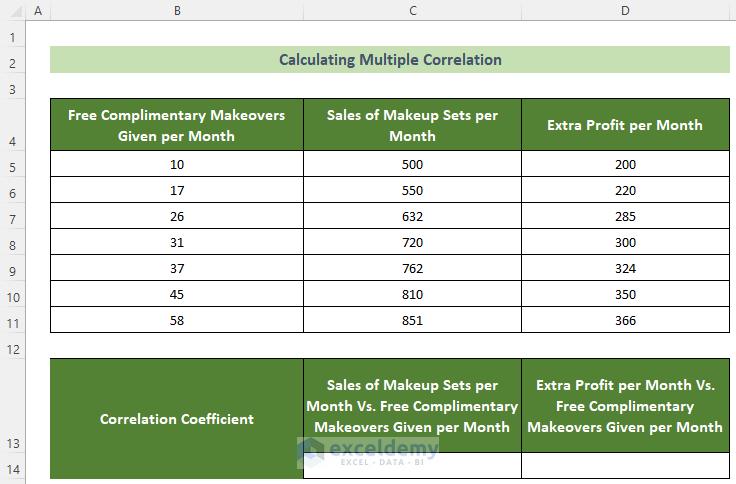
Multiple Correlation in Excel: Correlation Among More Than Two Variables
Now, it might happen that you have more than two variables in your dataset. And, you need to find the correlation between each pair of variables.
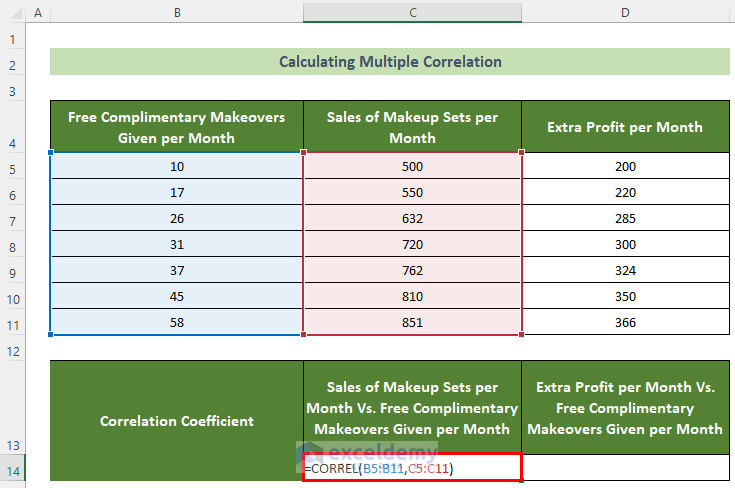
So, you have to find multiple correlations here. One is between the Sales of Makeup Sets per Month and the Free Complimentary Makeovers Given per Month. Another one is between the Extra Profit per Month and the Free Complimentary Makeovers Given per Month. To achieve this target, follow the steps below.
📌 Steps:
- Initially, click on the C14 cell and insert the following formula for the first and second variable’s correlation.
=CORREL(B5:B11,C5:C11)- Subsequently, hit the Enter button.
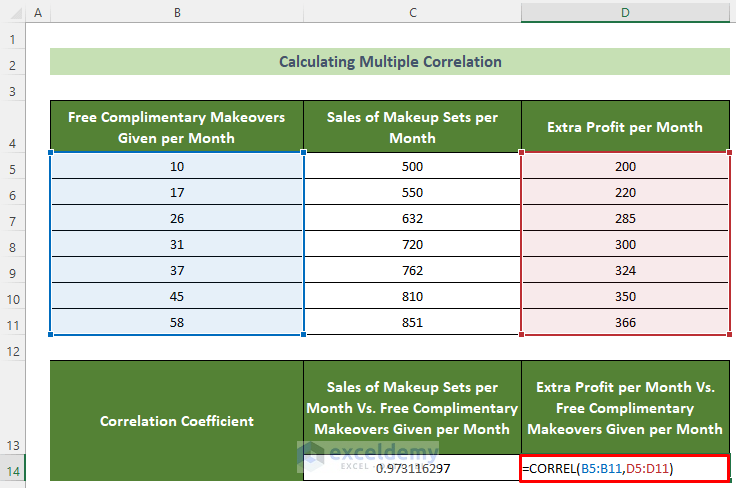
- Similarly, for the first and third variable’s correlation, click on the D14 cell and insert the following formula.
=CORREL(B5:B11,D5:D11)- Following, press the Enter button.
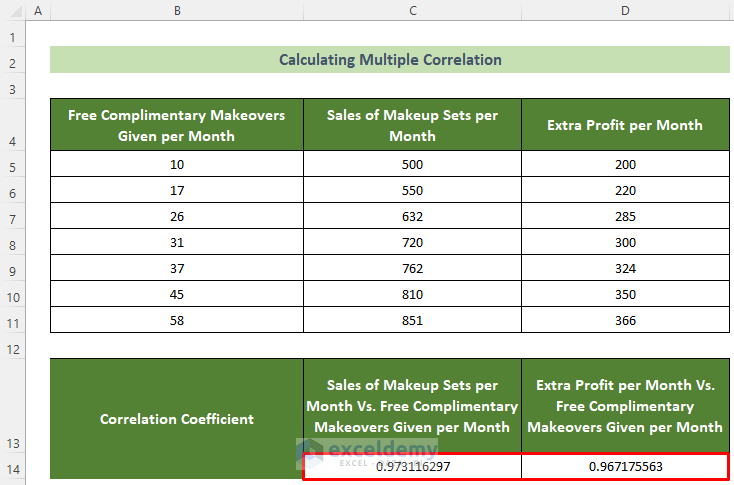
Thus, you have found multiple correlations between multiple variables and the final result should look like this.
Note:
You can also use the other 2 ways stated above to find multiple correlations in Excel.
💬 Things to Remember
- We cannot use these correlation results to indicate a cause and effect relationship, since the increase in sales of makeup sets per month may also be influenced by other factors such as an increase in ads in print media advertising the makeup sets for example.
- If you want to find the exact cause and effect relationship, you will have to use linear regression.
Download Practice Workbook
You can download our practice workbook from here for free!
Conclusion
So, in this article, I have shown you 3 simple and suitable ways to find correlations between two variables in Excel. I suggest you read the full article carefully and practice accordingly to understand better. I hope you find this article helpful and informative. You are very welcome to comment here if you have any further questions or recommendations.
Thank you!
Related Articles
- How to Make a Correlation Scatter Plot in Excel
- How to Calculate Correlation between Two Stocks in Excel
- How to Do Correlation and Regression Analysis in Excel
- How to Interpret Correlation Table in Excel
- How to Make Correlation Heatmap in Excel
- How to Calculate Partial Correlation in Excel