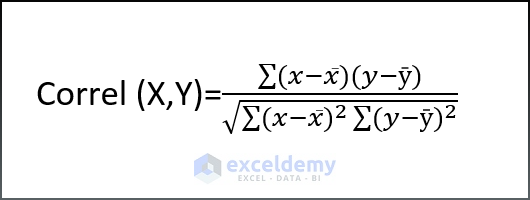Mohammad Shah Miran
In statistical analysis, performing Correlation and Regression calculations is the popular way to analyze and predict future events. However, there are several ways to calculate Correlation and Regression for a specific set of data. In this article, we will show a simple demonstration of how to do Correlation and Regression Analysis in Excel.
The below image depicts a complete output of Linear Regression analysis which you will get upon completion of the task.
Download Practice Workbook
You can download and practice the dataset that we have used to prepare this article.
Introduction to Correlation and Regression
Correlation is an expression of how closely two variables are linearly related to each other. It is a typical technique for describing apparent connections without explicitly stating any cause and consequence.
In statistical analysis, Correlation is measured by a coefficient denoted by “r”.
Let’s assume a set of data labeled by two variables X and Y. Thus the Correlation Coefficient can be formulated such as
Where,
- x̄ and ȳ are the sample means AVERAGE of X variable and AVERAGE of Y variable respectively.
On the other hand, Regression analysis is a statistical technique devoted to estimating the connection between one dependent and two or more independent variables. It can be used to simulate the long-term link between variables and evaluate the future outcome of the dependent variable. For Linear Regression Analysis, a linear line equation can be formulated as below,
Where,
- Y is the dependent variable, and X is the independent variable. m is the slope of the straight line.
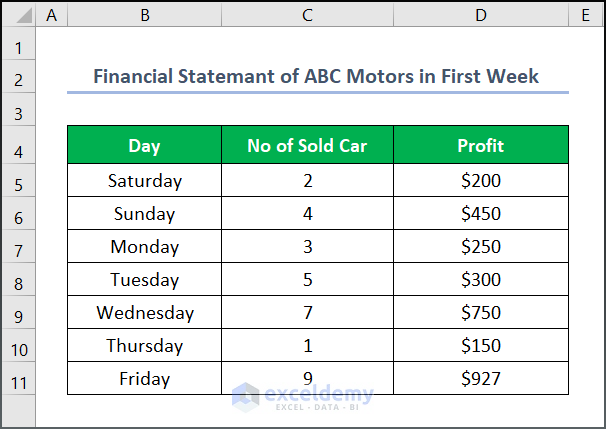
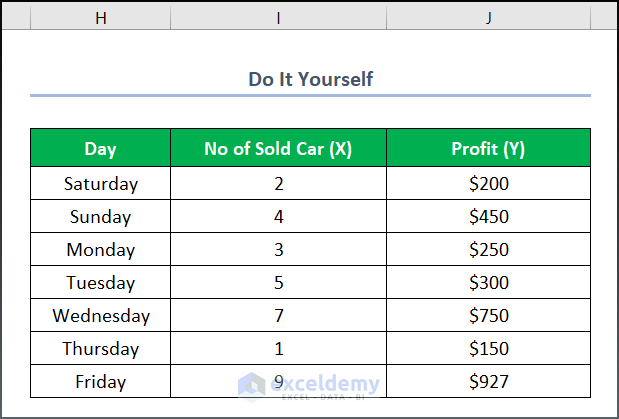
Here, we have chosen a dataset named “Financial Statement of ABC in First Week” to accomplish our task. However, you may select any dataset that is suitable for you.
Here, we have used the Microsoft Excel 365 version; you may use any other version according to your convenience.
Read More: How to Calculate Intraclass Correlation Coefficient in Excel
2 Quick Steps to Perform Correlation and Regression Analysis in Excel
In Excel, there are several methods to perform Correlation and Regression analysis, such as using the CORREL, PEARSON, INTERCEPT, SLOPE functions, or utilizing Scatter Chart, Analysis ToolPak Add-in, etc. However, as our primary objective is to make an Excel sheet with both Correlation and Regression analysis for one specific dataset, we will incorporate two different methods to accomplish the task. However, in the following section, we will add one more method to help you understand the relevant methods and functions.
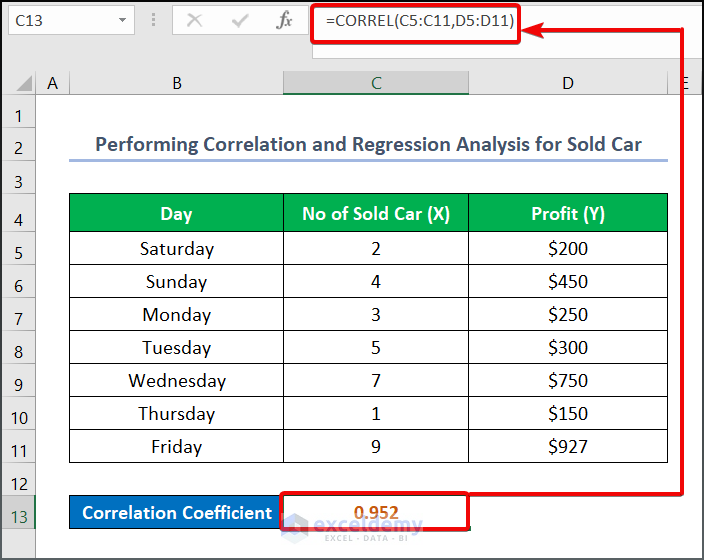
Step 1: Calculate the Correlation Coefficient
- Write the following formula in cell C13.
=CORREL(C5:C11,D5:D11)- Press the ENTER button to see the output.
Read More: How to Calculate Partial Correlation in Excel (3 Suitable Ways)
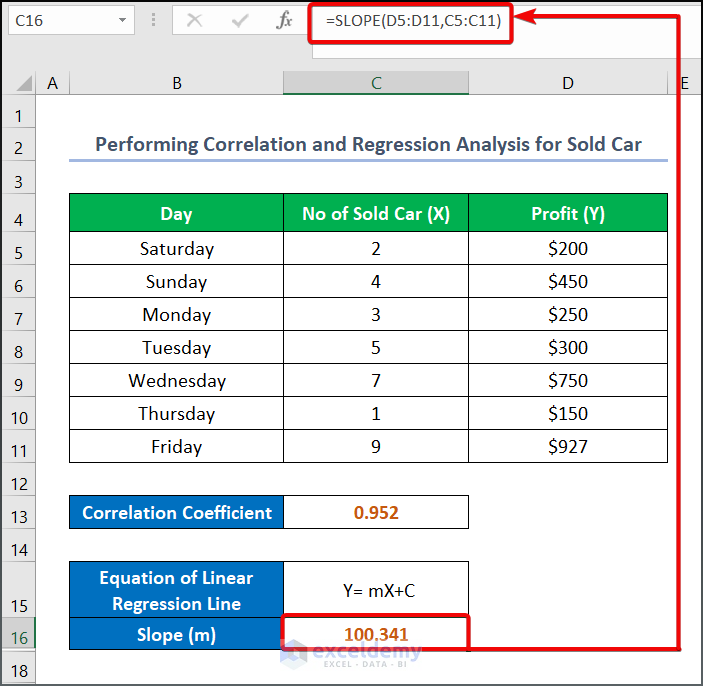
Step 2: Compute the Constant and Intercepting value for Regression Line
- Enter the following formula in cell C16 to calculate the slope value.
=SLOPE(D5:D11,C5:C11)- Hit the ENTER button to see the output.
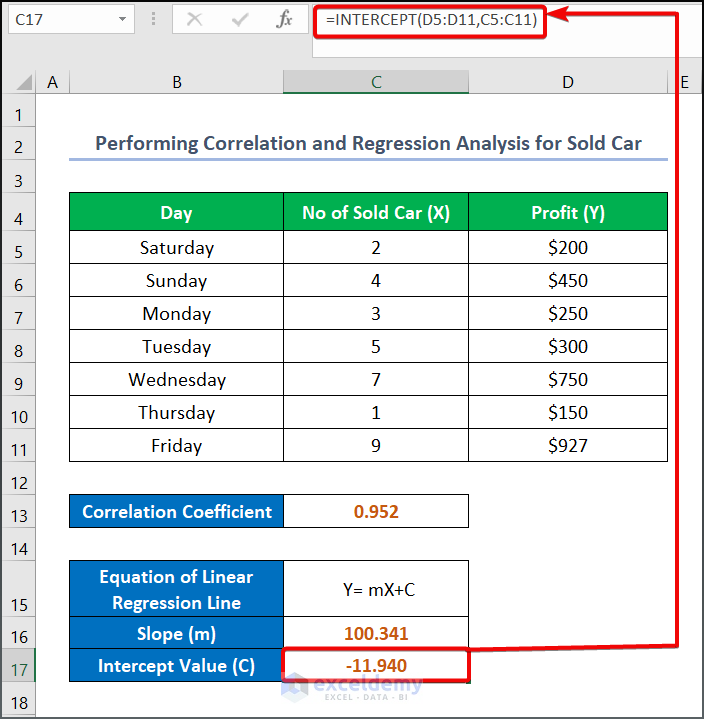
- Following that, write the following formula in cell C17 to compute the intercepting value of the Regression line.
=INTERCEPT(D5:D11,C5:C11)- Hit the ENTER button afterward.
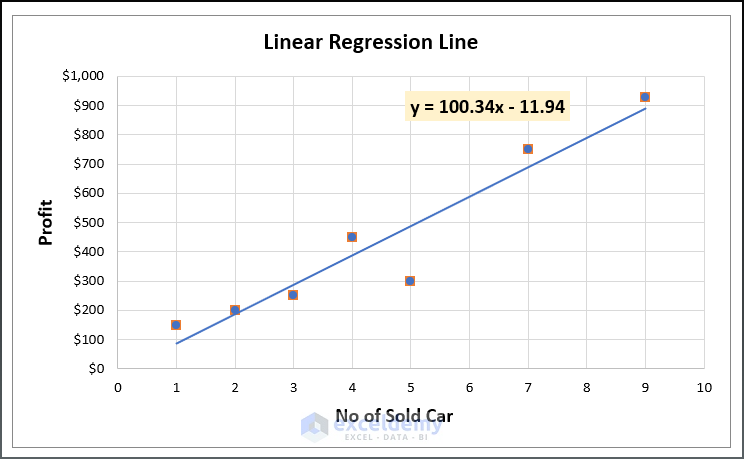
Here, the Correlation Coefficient indicates how closely the data point aligns with the Regression line. The given dataset’s correlation coefficient value of 0.952 indicates that the data points are closely aligned with the created trendline. However, the Slope value of the Regression line shows the amount of profit change per the number of cars sold. The intercept value indicates that the profit will be -11.940 when the number of cars sold is zero.
Similar Readings
- How to Make a Correlation Matrix in Excel (2 Handy Approaches)
- Calculate P Value for Spearman Correlation in Excel
- Find Correlation Between Two Variables in Excel (3 Easy Ways)
How to Do Correlation Analysis in Excel
Although we have seen one of the ways to find the Correlation Coefficient for a set of data in the previous method, here we are adding one more method at your disposal for your better understanding. Other than the CORREL function, here we will use the PEARSON function to accomplish the task.
📌 Steps:
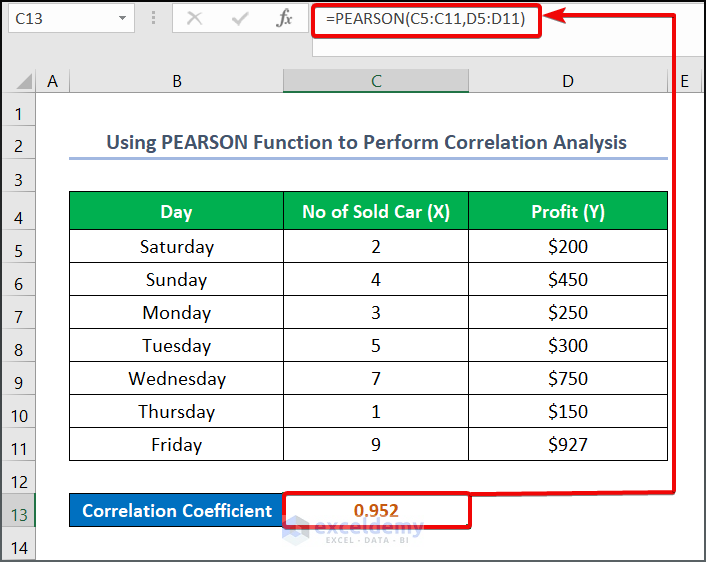
- Go to the C13 cell >> enter the formula as given below >> press the ENTER key.
=PEARSON(C5:C11,D5:D11)
Read More: How to Calculate Pearson Correlation Coefficient in Excel (4 Methods)
How to Accomplish Regression Analysis in Excel
There are several methods to perform a Regression analysis in Excel. Here, we will see how to do Regression analysis by using an Excel Chart.
📌 Steps:
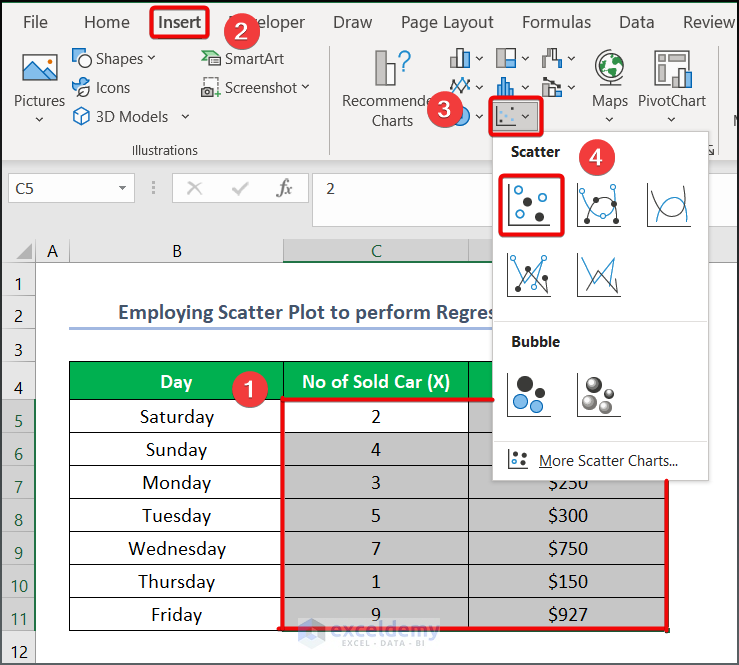
- Select the range of the dataset from C5:D11, then navigate to the Insert tab >> Charts group >> Insert Scatter or Bubble Chart group >> Scatter.
You will get an output as given below
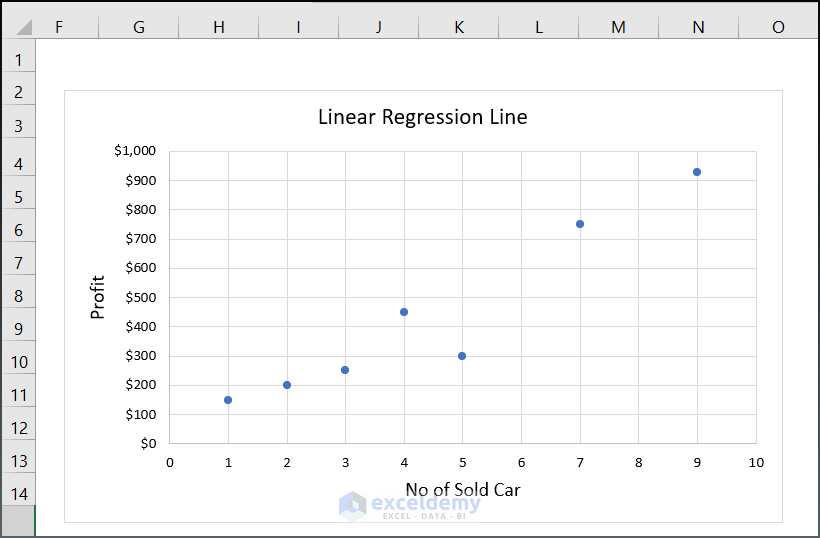
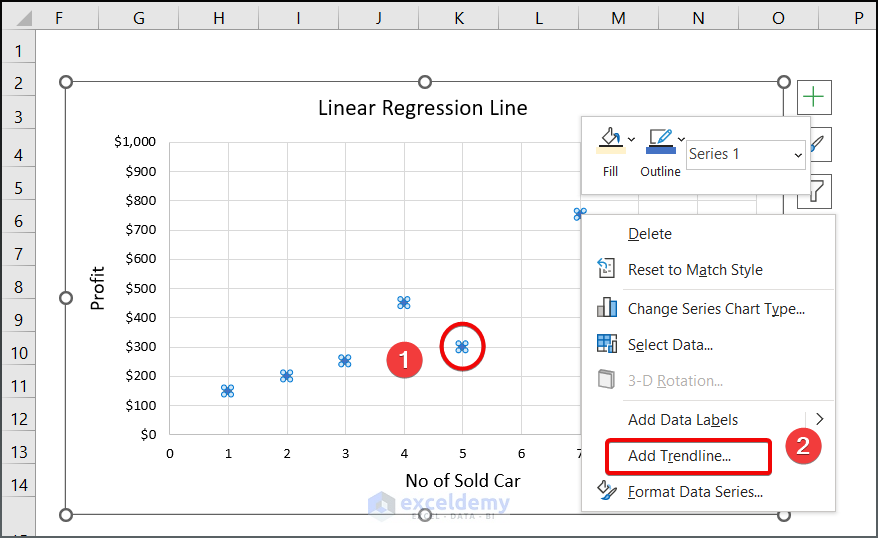
- After that, click one of the data points on your chart, then do Right-click on your mouse.
- Press on the Add Trendline option.
- Now on the right side of your Excel interface, a wizard will appear.
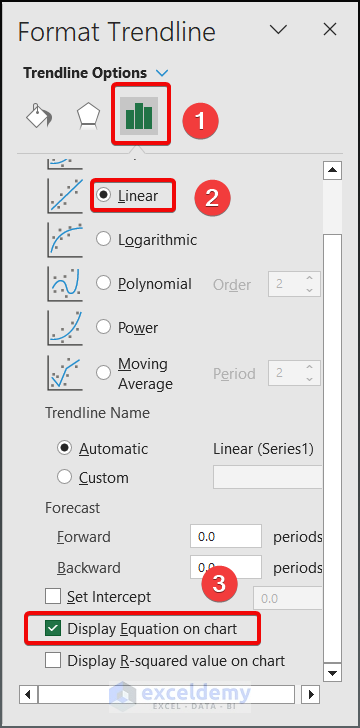
- Select Linear as your Trendline option.
- Later, select Display Equation on Chart.
Finally, you will get the final output along with the Trendline as given below.
Read More: How to Make a Correlation Scatter Plot in Excel (2 Quick Methods)
Practice Section
We have provided a Practice section on the right side of each sheet so you can practice yourself. Please make sure to do it yourself.
Conclusion
In this article, we have discussed how to do Correlation and Regression Analysis in Excel. As you have already understood, there are plenty of ways to do this task. So before going through a specific method, ensure the method you choose aligns with your work. Further, If you have any queries, feel free to comment below and we will get back to you soon.
Related Articles
- How to Make Correlation Graph in Excel (with Easy Steps)
- Find Spearman Rank Correlation Coefficient in Excel (2 Ways)
- How to Calculate Cross Correlation in Excel (2 Suitable Ways)
- Calculate Autocorrelation in Excel (2 Ways)
- How to Calculate Spearman Correlation in Excel (3 Easy Methods)
- Interpret Correlation Table in Excel (A Complete Guideline)
