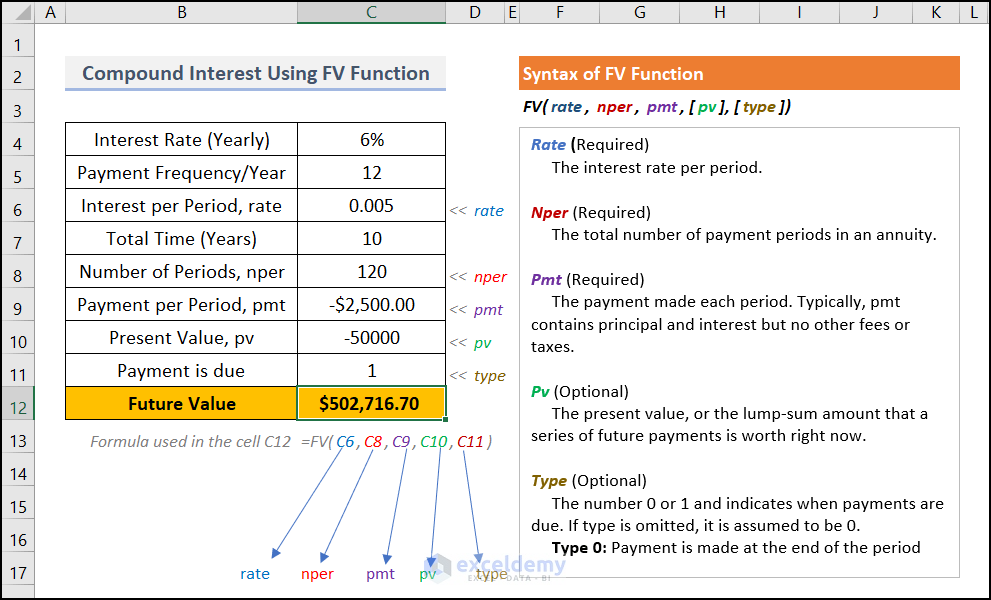
The following image provides an overview of the calculation process of compound interest in Excel using the FV function.
Calculate Compound Interest Using Excel Formula with Regular Deposits: 2 Methods
Say, you’re going to run a savings scheme with one of your trusted banks. You want to know what your total amount after a certain period (years) will be.
Method 1 – Using the FV Function
The FV function returns the future value of an investment based on periodic, constant payments and a constant interest rate.
Steps:
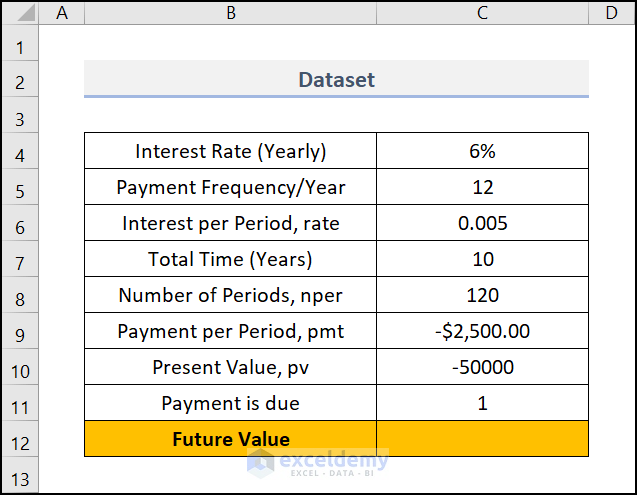
- Make sure to input all the values in the appropriate cells.
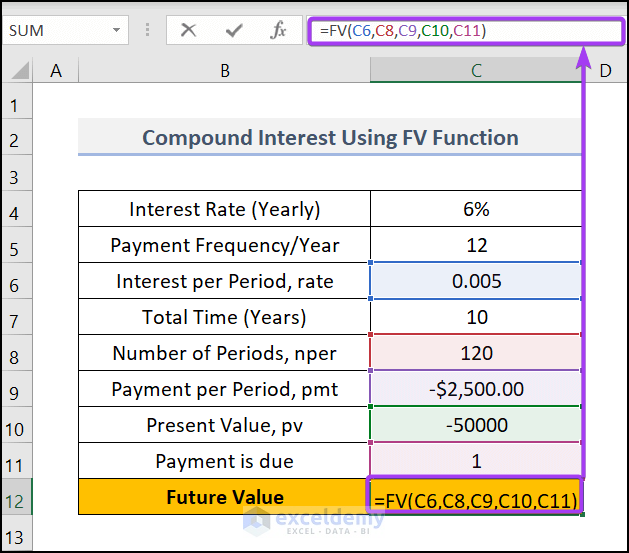
- Select cell C12 and insert the following formula.
C6=Interest Per Period, (rate)
C8=Numbers pet periods, (nper)
C10=Payment per period, (pmt)
C11=Present Value, (pv)
The syntax FV(C6,C8,C9,C10,C11) returns the future value by compound calculation.
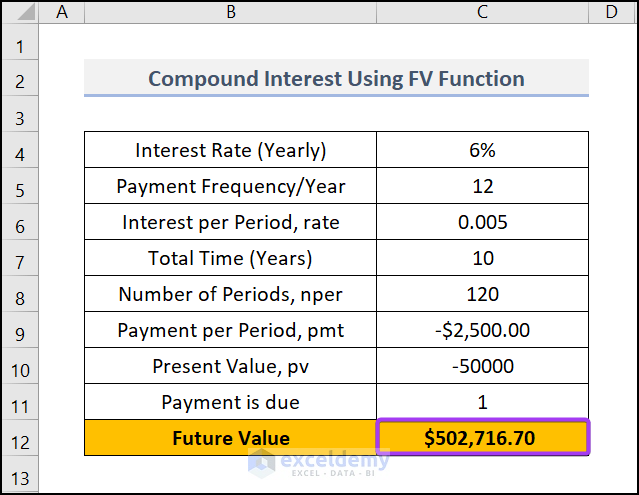
- Press Enter and the formula will display the future value.
Read More: Formula for Monthly Compound Interest in Excel
Method 2 – Calculate Compound Interest with Regular Deposits Using a Manual Formula
Steps:
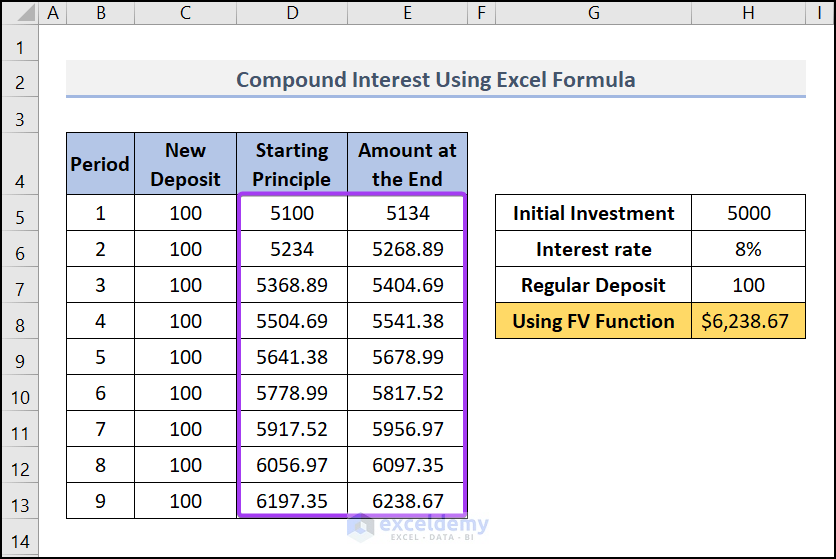
- We have put only 9 months or periods (under the Period column). Add more periods under this column if necessary and apply the formulas from the above row.
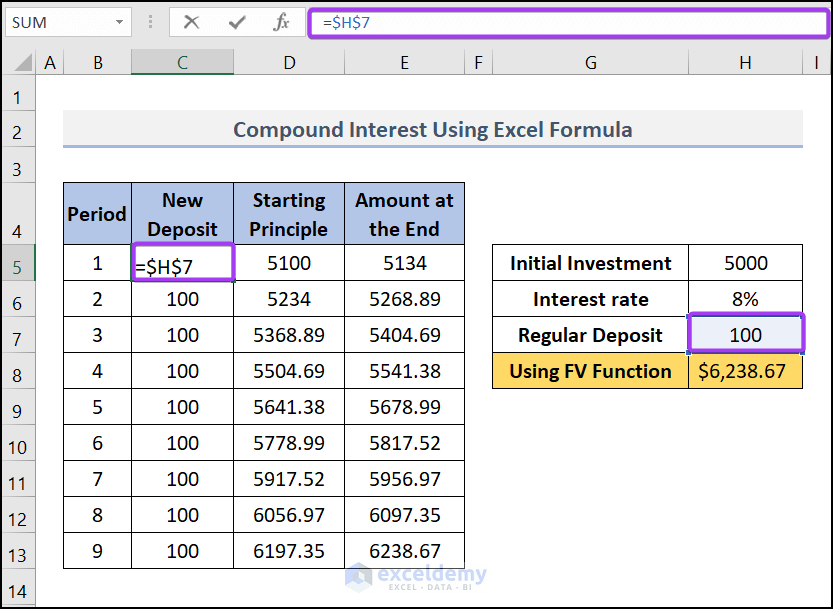
- In cell C5 (under the column “New Deposit”), use this formula, C5=$H$7.
- Apply this formula to other cells in the column.
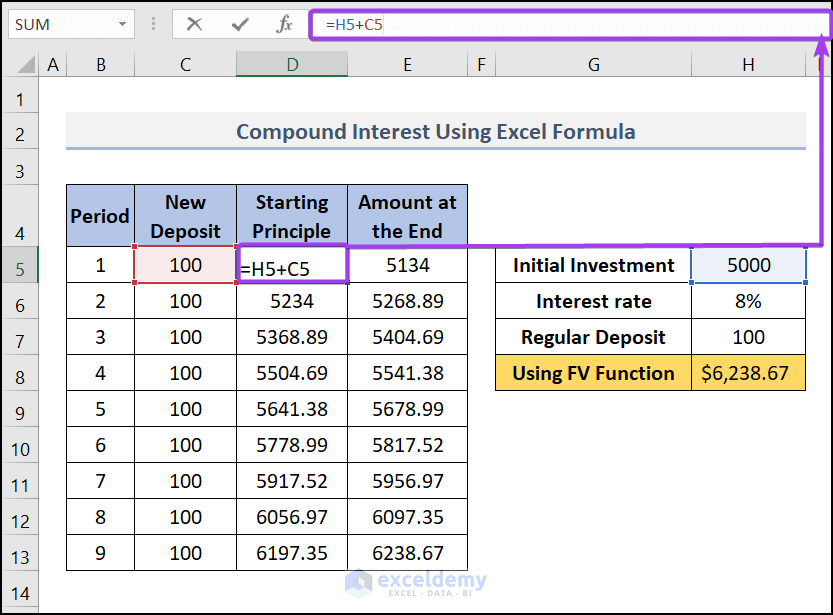
- In cell D5 (under the column Starting Principle), use this formula, D5=H5+C5.
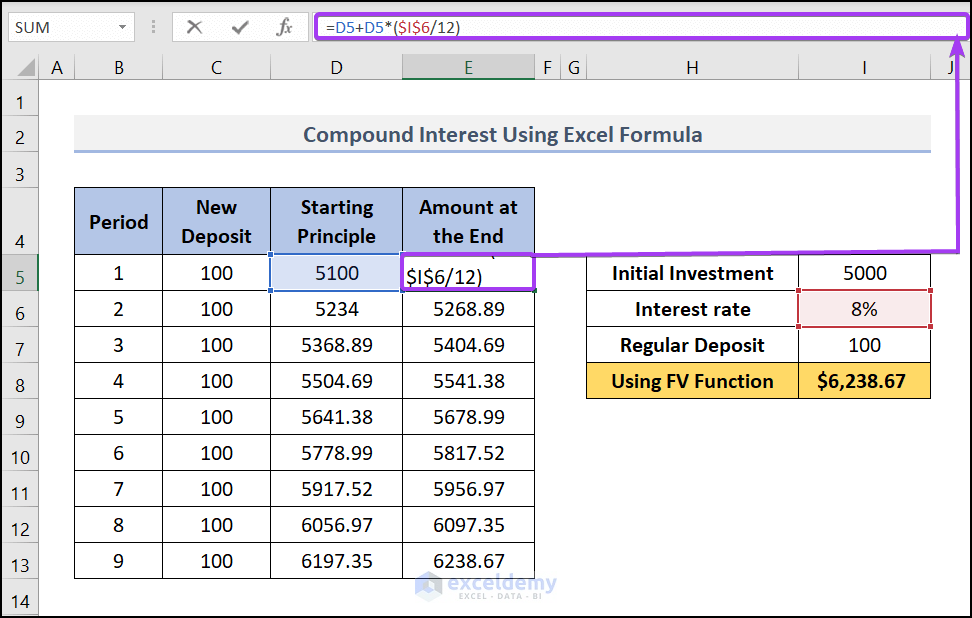
- In cell E5 (under the column Amount at the End), use this formula, E5=D5+D5*($I$6/12)
This formula will add the Starting Principle (D5) to the interest earned (D5*($I$6/12)) for the period. We are dividing the yearly interest rate $I$6 by 12 as the regular deposit is made monthly. Copy the formula and apply it to the cells below.
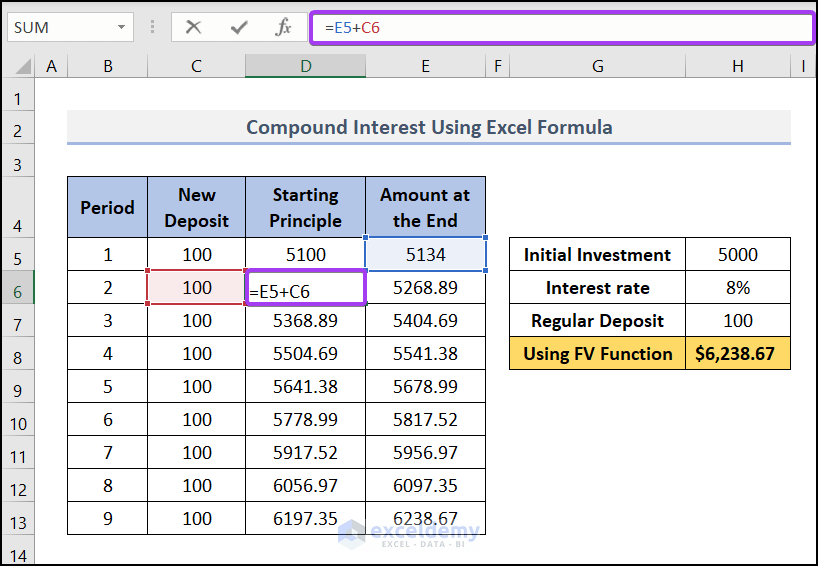
- In cell D6 (under the column Starting Principle), use this formula, D6=E5+C6. This formula will add the new deposit to the amount at the end of the previous period. Then we copied down this formula for other cells in the column.
- Drag down the Fill Handle tool for other cells and your result will look like this.
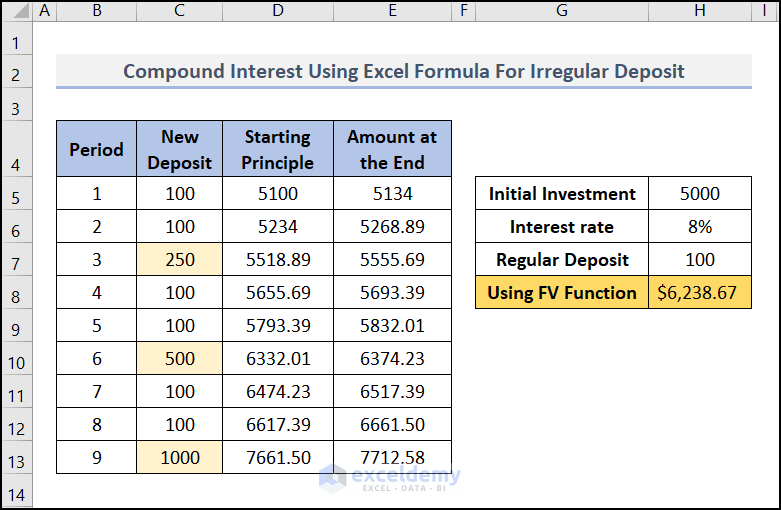
Using the Template to Calculate the Compound Interest with Irregular Deposits
We can extend the previous template to calculate compound interest with irregular deposits. Insert your irregular deposits manually in the “New deposit” column like the image below.
Read More: Methods to Apply Continuous Compound Interest Formula in Excel
Practice Section
Here, we have provided a Practice section on each sheet on the right side for your practice.
Related Articles
<< Go Back to Compound Interest in Excel | Excel for Finance | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!


Kawser, excellent tutorial. You have a gift for clear explanation.
May I ask guidance setting up a “statement” for an 18-year-old grandson who has not yet learned to handle money.
I no longer want him to receive a birthday gift = his age x $100, instead to hold it in the “Bank of Grandpa” until he has demonstrated some maturity or has a valid need (rent, car, etc) for his money. (Yes, it’s occurred to me to not change the plan, to let him squander his money and then feel regret later, but I would feel more regret than him.)
I know the basics of Excel but can’t figure out how to set up a spreadsheet showing irregular deposits ($1900, then $2000, and so on, along with random gifts throughout the year) earning 2% annually with quarterly compounding.
The spreadsheet would be his “statement,” like the statement our bank gives us once a month, to let him see how much money he has with us.
Can you provide me a sample spreadsheet with the needed formulas, please?
Many thanks.
— Steve K.
At first, Create a dataset having Age in Column B, Fixed Amount in Column C and Principle At the Start of the period in Column D.
Then, insert the following formula in cell D5 and use the Fill Handle option to apply it to all cells of column D.
=B5*C5
Finally, insert the following formula in cell E6 and use the Fill Handle option to apply it to all cells of column E to get the desired result.
=E5*(1+0.02)+D6
The excel file is added here according to your wish.
Compound Interest Statement.xlsx
Thanks and happy helping.
Zehad
I was wondering if you ever do projects for people? I would like to have a couple of spreasheets built out and I’m curious what you would charge. My email is [email protected]
Thank you
Bo Thibaut
Dear Bo Thibaut,
We are willing to do any Excel-related projects. Kindly share your requirements through this Email: [email protected]
Regards
Shamima Sultana
Project Manager | ExcelDemy