Akib Bin Rashid
Excel is the most widely used tool for dealing with massive datasets. We can perform myriads of tasks of multiple dimensions in Excel. In this article, I will show you how to plot Weibull Distribution in Excel.
Download Practice Workbook
Download this workbook and practice while going through the article.
Introduction to Weibull Distribution
The Weibull Distribution is a continuous probability distribution that is used to analyze life data, model failure times, and assess the reliability of access products. This distribution can be used largely in different fields to analyze data.
Reliability Function R(t) = e^-[{(t-γ)/α}^β]
Where,
β = Shape Parameter
α = Scale Parameter
γ = Location Parameter. This is usually 0.
From R(t), we can get the Failure function F(t)
F(t) = 1-R(t)
After calculation, we get
ln(ln(1/(1-F(t))) = βlnt-βlnα
This resembles the y=mx+c equation
4 Quick Steps to Plot Weibull Distribution in Excel
This is the dataset for today’s article. We have the instances of failure and the number of days for the failure. For example, the 1st failure occurs after 400 days, 2nd one after 820 days.
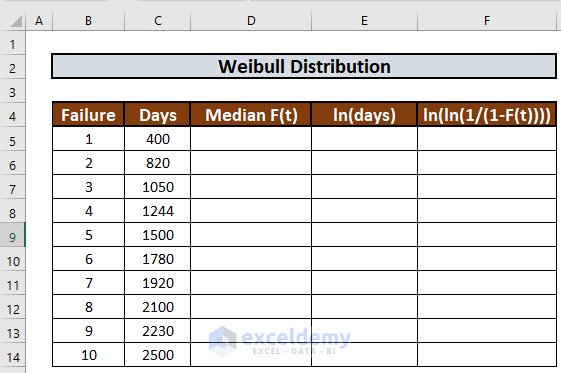
I will use this data to get the Weibull Distribution and understand the failure rate.
Step 1: Calculate Median Rank
The first step is to calculate the median rank. To calculate this, we will use Bernard’s approximation.
- Go to D5 and write down the following formula
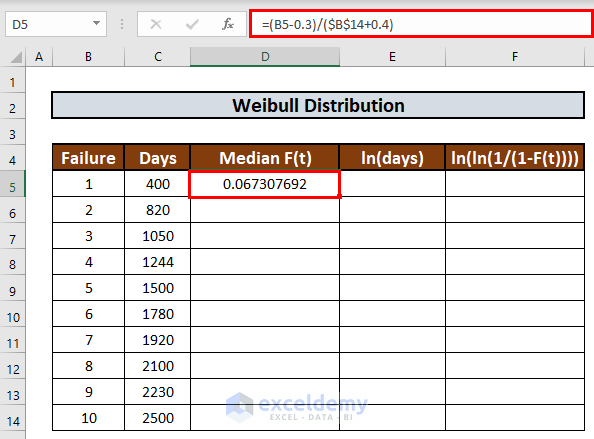
=(B5-0.3)/($B$14+0.4)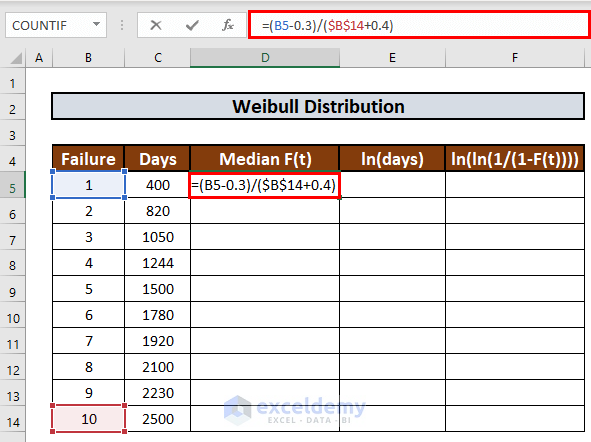
- Then, press ENTER to get the output.
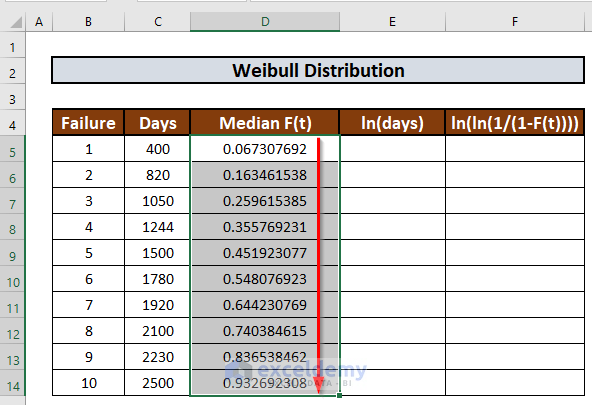
- After that, use the Fill Handle to AutoFill up to D14.
Step 2: Determine Natural Logarithm
The next step is to calculate the natural logarithm as per the requirement. First, we will determine the logarithm of days. To do so,
- Go to E5 and write down the following formula
=LN(C5)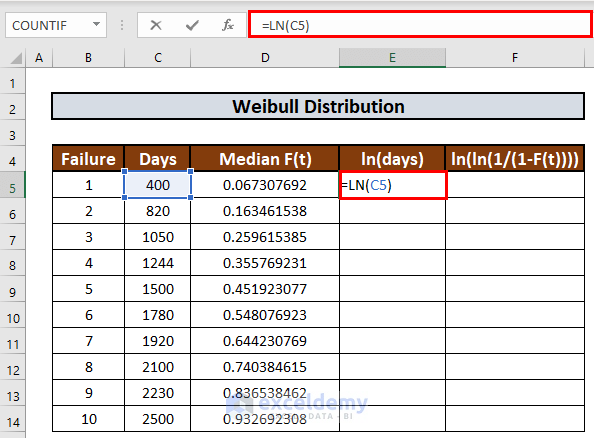
- Then, press ENTER to get the output.
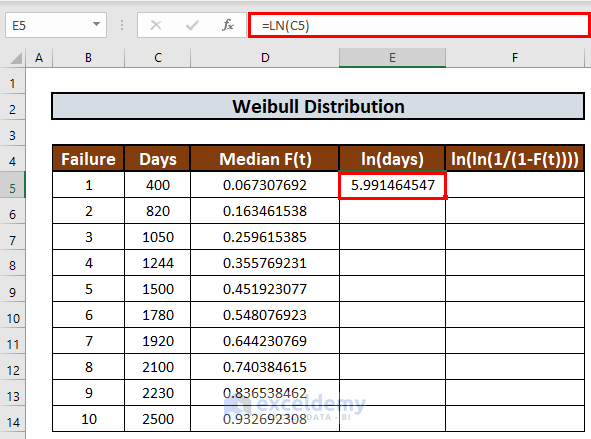
- After that, use Fill Handle to AutoFill up to E14.
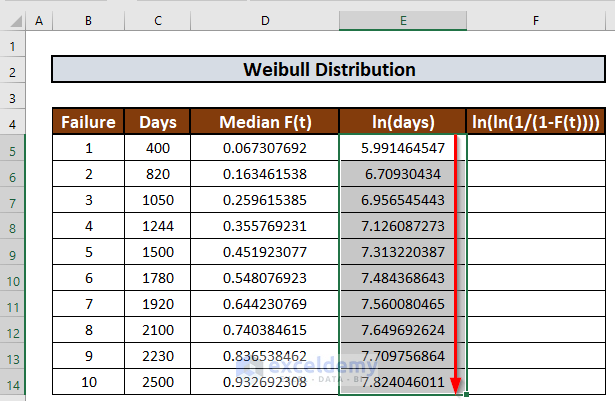
- In a similar way, we will fill up the next column. The formula in F5 will be
=LN(LN(1/(1-D5)))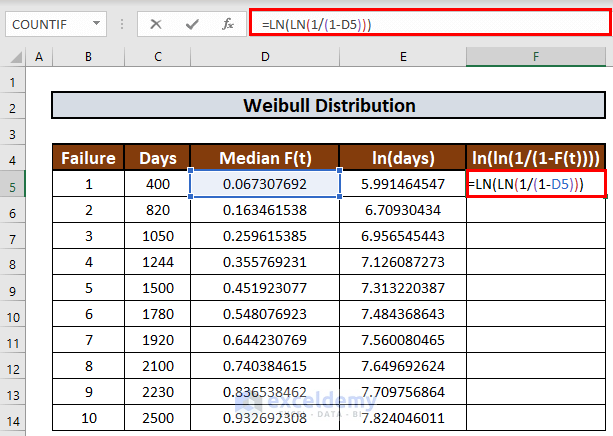
- Then, press ENTER to get the output.
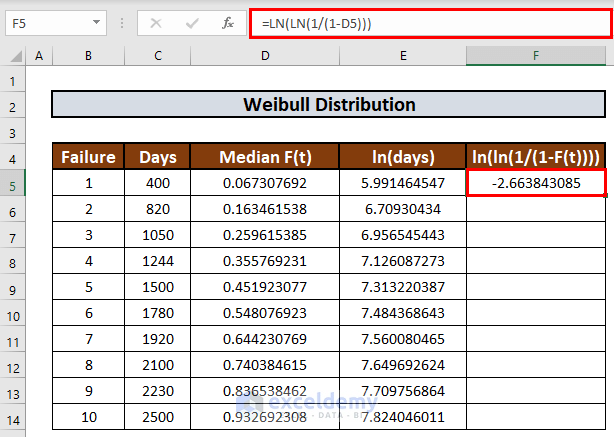
- After that, use Fill Handle to AutoFill up to F14.
Read More: How to Plot Normal Distribution in Excel (With Easy Steps)
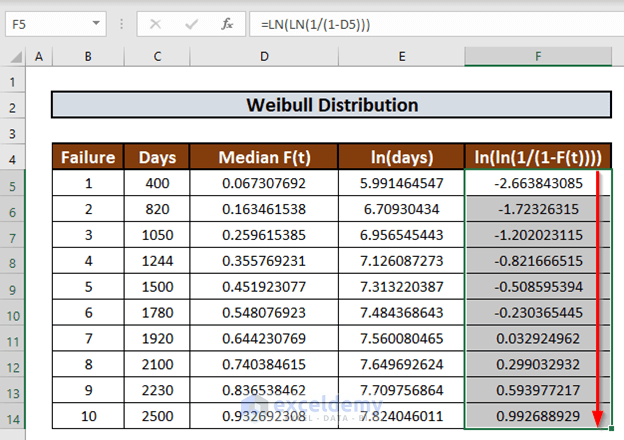
Step 3: Plot Distribution Chart
The next step is to plot a chart using ln(days) as x-axis and ln(ln(1/(1-F(t)))) as y-axis. To do so,
- Select E4:F14.
- Then, go to the Insert
- After that, choose the Scatter
- Finally, select the one you like.
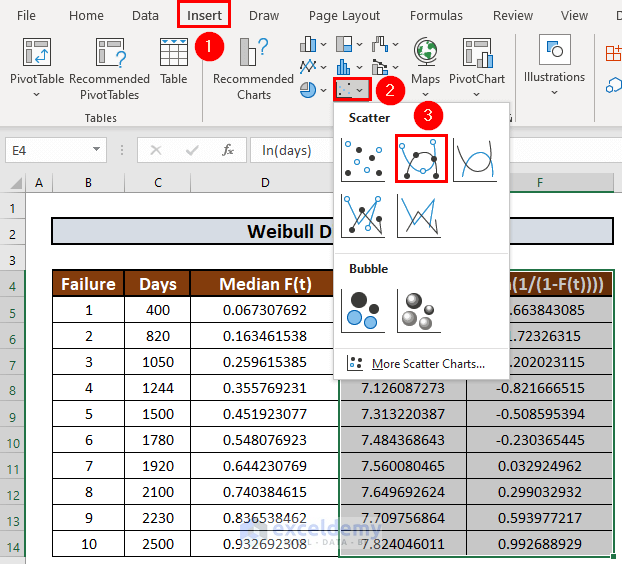
- Excel will create a scatter plot.
- Rename the plot to Weibull Distribution.
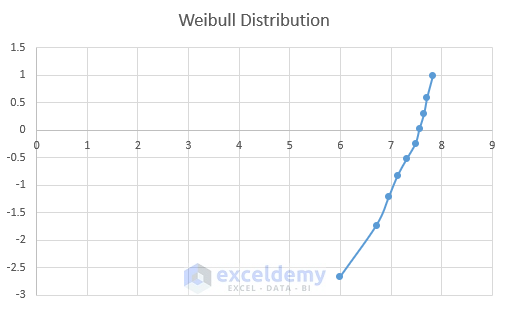
Read More: How to Make a Cumulative Distribution Graph in Excel
Step 4: Compare Equation to Determine Coefficients
Now, we will determine the parameters. We will get the trendline equation and compare it with the equation ln(ln(1/(1-F(t))) = βlnt-βlnα
- Go to Chart Design.
- Then, go to Add Chart Element.
- After that choose a Trendline.
- Excel will add a trendline.
- Select the trendline and right-click your mouse.
- Then, select Format Trendline.
- After that, mark the box for Display Equation on Chart.
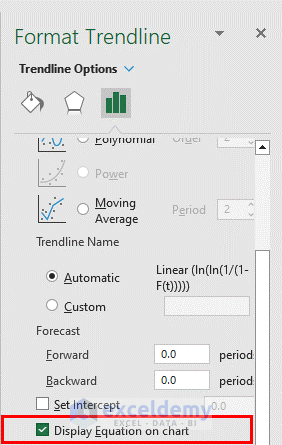
- Excel will show the equation.
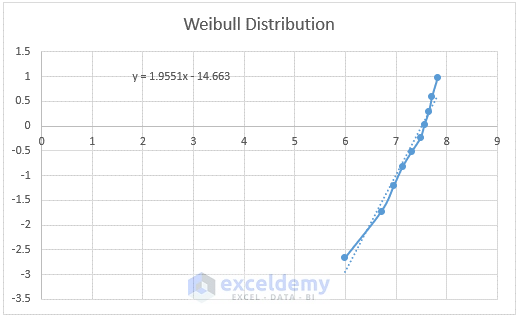
- The equation is y=1.9551x-14.663. After comparing with ln(ln(1/(1-F(t))) = βlnt-βlnα, we get
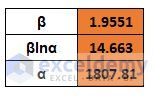
- β = 1.9551
- βlnα = 14.663
- Using these values, we get
- α = 1807.811
- So, the Reliability Function becomes
R(t) = e^-[(t/1807.811)^1.9551]
Read More: How to Make a t-Distribution Graph in Excel (with Easy Steps)
Things to Remember
The shape parameter indicates the failure rate.
- If β < 1, then the failure rate decreases with time
- If β = 1, then the failure rate is constant
- If β > 1, the failure rate increases with time
Use absolute reference to lock a cell.
Conclusion
In this article, I have explained how to plot Weibull Distribution in Excel. I hope it helps everyone. If you have any suggestions, ideas, or feedback, please feel free to comment below. Please visit Exceldemy for more useful articles like this.
