Excel Solver Exercises: 8 Advanced Problems

This tutorial contains eight exercises related to the Excel solver.

These problems are quite difficult to solve, requiring an advanced level of Excel knowledge, including knowledge of: the SUM, SUMPRODUCT, HLOOKUP, COUNTIF, IF, and OR functions and Enable solver, solver properties, solver example, choosing the best project, portfolio optimization with solver, solver for linear programming, usage of solver to minimize cost, assign work using an evolutionary solver, and schedule optimization.

Excel 2010 or later is required to solve all the exercises.

Download Practice Workbook

Solver Exercises.xlsx

Problem Overview

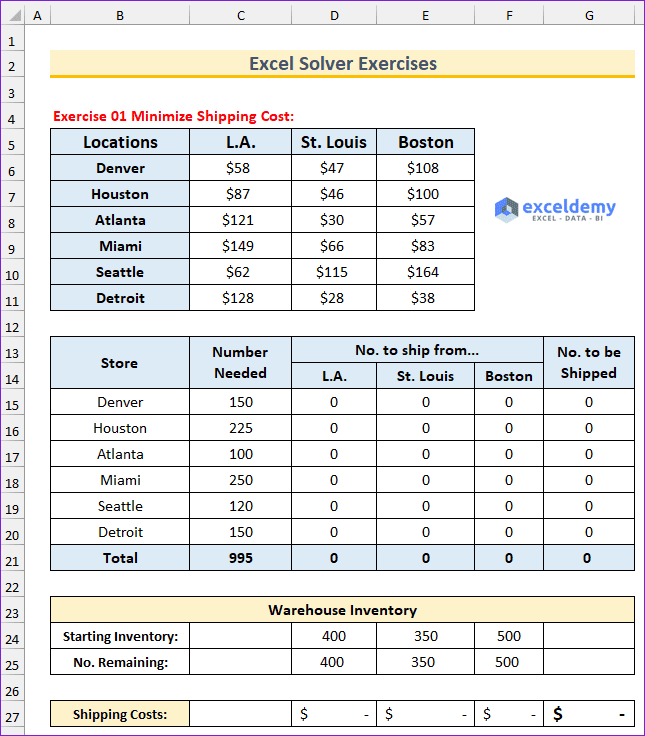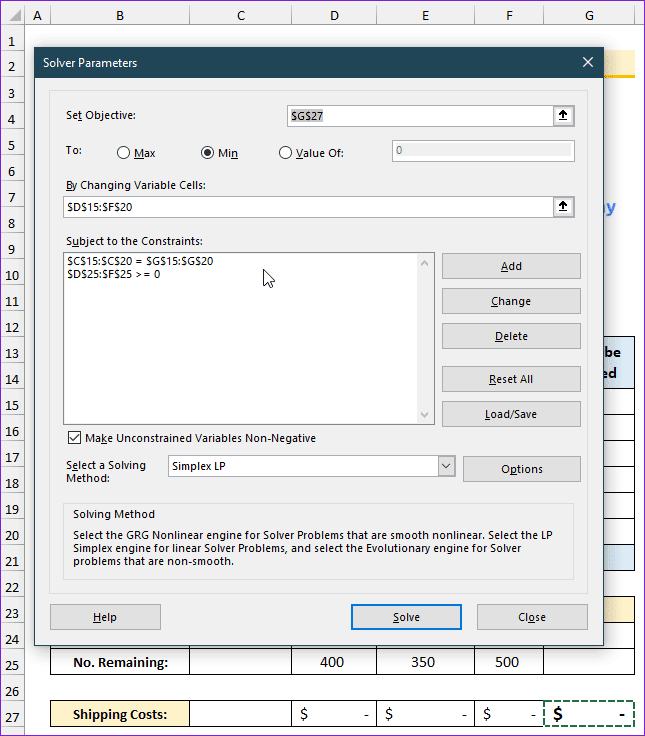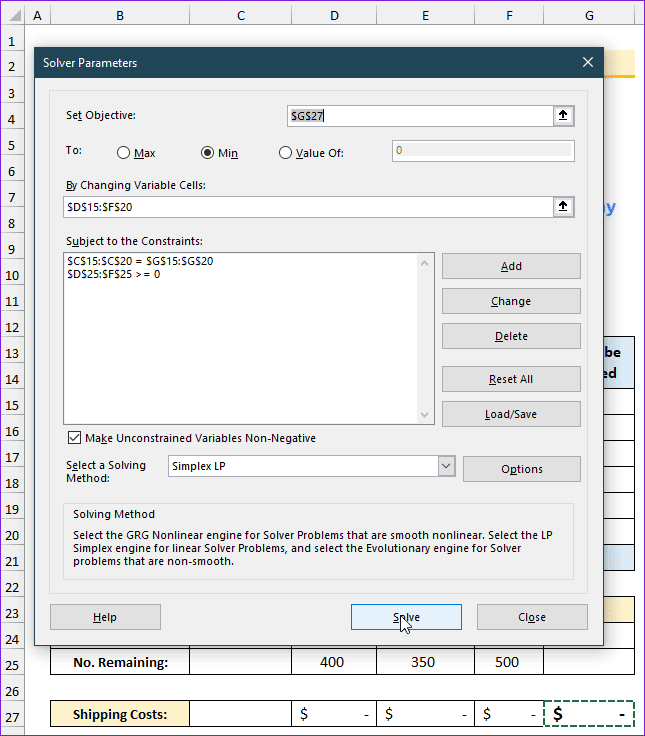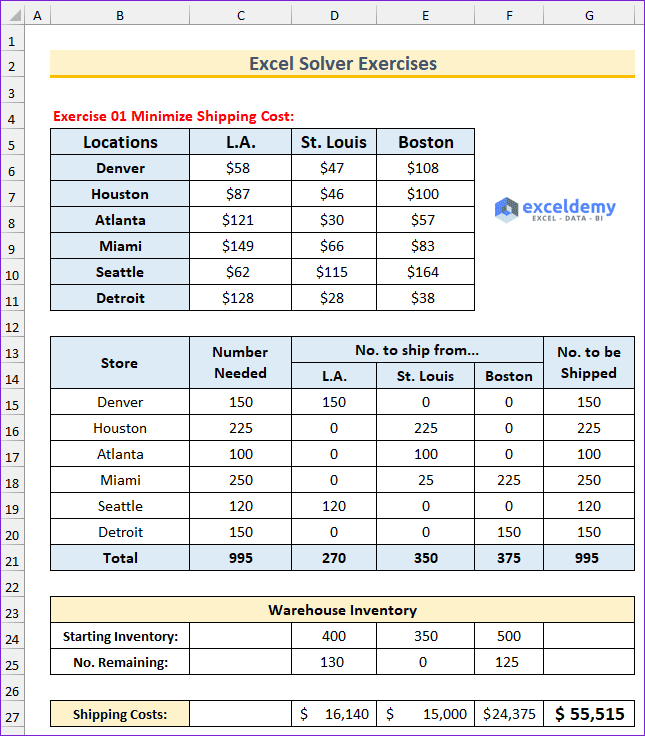
In the downloadable file “Solver Excercises.xlsx” above, the “Problem” sheet shows the exercises, and the “Solution” sheet shows the problems worked out. Additionally, the solver settings for each exercise are provided in the “Reference” sheet. Load the values from this sheet into the solver for each problem. To illustrate, the following image shows the first problem to be solved.

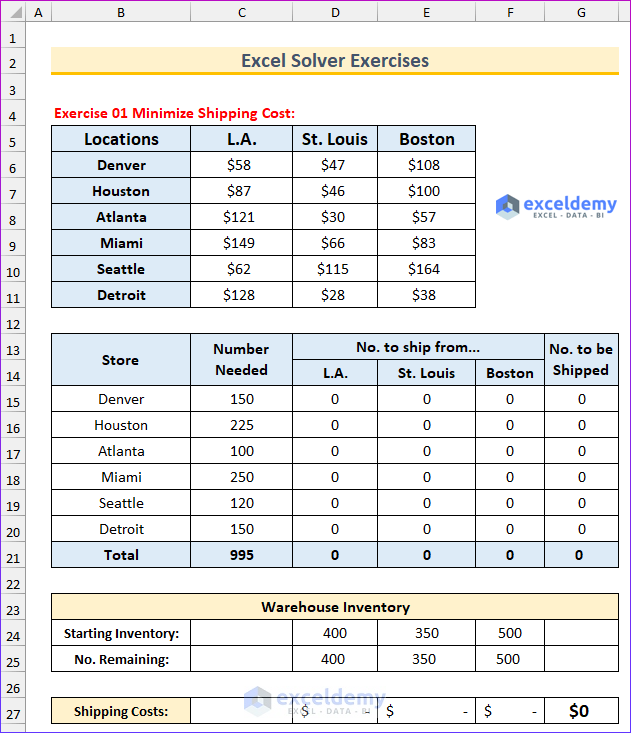
Exercise 1 – Minimize Shipping Cost

A company has warehouses in St. Louis, Los Angeles, and Boston. Six retail outlets are situated all over the United States. These retail outlets take orders from customers. The company then ships products from one of the warehouses. The company aims to supply all six retail locations with the products they require from the stock that is currently on hand in the warehouses. While shipping products to outlets, the company wants to keep shipping charges as low as possible.
- The first table shows the shipping costs from one port to another. The second table shows the product requirement for each port. After that, there is a table that contains the information about the warehouse inventory. Your task is to use the solver to find the values that will minimize the shipping costs from the warehouses to the outlets.
- Solution: Solver Parameters are as follows:
  - Set Objective: G27
  - To: Min
  - By Changing Variable Cells: D15:F20
  - Subject to the Constraints: C15:C20=G15:G20, D25:F25>=0
  - Select a Solving Method: Simplex LP

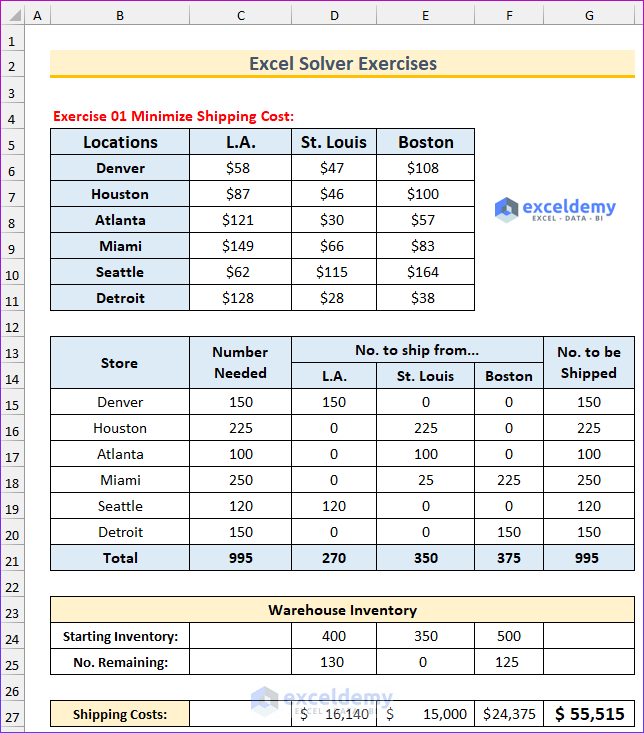
The following animated image shows the solution to the first problem.

Exercise 2 – Minimize Production Cost

Mix different raw materials to produce different types of steel, such as regular, exclusive, and super quality steel. There is data about the availability and cost of these raw materials, as well as their quality rating. Additionally, establish the required amount of production, the price per ton of different classes of steels, and their minimum rating. The conditions are given in the dataset.
- Solution: Solver Parameters are as follows:
  - Set Objective: I38
  - To: Min
  - By Changing Variable Cells: C32:E34
  - Subject to the Constraints: C35:E35>=C37:E37, C41:E41>=C43:E43,F32:F34<=H32:H34
  - Select a Solving Method: Simplex LP

Exercise 3 – Maximize Profit of Products

Profit per unit is given for 17 products. Your task is to find the maximum profit using the solver.
- The combined production capacity is 300 units per day.
- The company needs 50 units of Product A to fill an existing order.
- The company needs 40 units of Product B to fill an expected order.
- The market for Product C is relatively limited, so the company is not interested in producing more than 40 units of this product per day. Additionally, the Product D to Q should be greater than or equal to 15.
- Solution: Solver Parameters are as follows:
  - Set Objective: E65
  - To: Max
  - By Changing Variable Cells: C48:C64
  - Subject to the Constraints: C48>=50, C49>=40, C50<=40, C51:C64>=15,C65=400
  - Select a Solving Method: Simplex LP

Exercise 4 – Marketing Budget Allocation

Here, the current stats are on the left, and the portion where you are going to use the solver is on the right. Your task is to maximize the conversions (value of cell J83). The budget should be greater than or equal to 60 000, and the total solver budget and the total cost should be equal.
- Solution: Solver Parameters are as follows:
  - Set Objective: J83
  - To: Max
  - By Changing Variable Cells: H71:H82
  - Subject to the Constraints: H71:H82>=60000, H83=E83
  - Select a Solving Method: GRG Nonlinear

Exercise 5 – Schedule Optimization

The number of workers needed for a bank is provided. For example, 17 workers are needed on Monday, 13 workers are needed on Tuesday, 15 workers are needed on Wednesday, and so on. Moreover, all bank employees work five consecutive days. What is the minimum number of employees that this bank must have to meet its labor requirement?
- The condition, Total Number of Employee >= Number Needed, is given in row 96 and 98.
- Solution: Solver Parameters are as follows:
  - Set Objective: C100
  - To: Min
  - By Changing Variable Cells: B88:B94
  - Subject to the Constraints: B88:B94=integer, D96:J96>=D98:J98
  - Select a Solving Method: Simplex LP

Exercise 6 – Project Selection

Use an Excel solver to determine which projects should be undertaken in Excel.
- Find the maximum value of NPV.
- The year 1 value should be <=50,000,000 and year 2 value should be <=20,000,000.
- Selecting a project means 1 and discarding means 0.
- Solution: Solver Parameters are as follows:
  - Set Objective: C104
  - To: Max
  - By Changing Variable Cells: B107:B115
  - Subject to the Constraints: B107:B115=binary, C117:D117<=C118:D118
  - Select a Solving Method: Simplex LP

Exercise 7 – Investment Portfolio Optimization Based on Total Yield

The credit union is going to invest $5 million in various sectors. Find how this amount will be allocated using the following conditions:
- The amount that the credit union will invest in new-car loans must be at least three times the amount that the credit union will invest in used-car loans. The reason is that used car loans are riskier investments.
- Car loans should make up at least 15% of the portfolio.
- Unsecured loans should make up no more than 25% of the portfolio.
- At least 10% of the portfolio should be in bank CDs.
- The total amount invested is $5,000,000.
- All investments should be positive or zero.
- Solution: Solver Parameters are as follows:
  - Set Objective: C132
  - To: Max
  - By Changing Variable Cells: D125:D129
  - Subject to the Constraints: D125>=D126*3, D130=C122, F128<=0.25, F129>=0.1, F132>=0.15
  - Select a Solving Method: GRG Nonlinear

Exercise 8 – Assign Department

In this last Excel solver exercise, you will need to assign 40 employees to four Departments. The head of each department has rated each employee’s competence on a 0 to 10 scale (10 being most competent). Each employee has rated his satisfaction with each job department (again on a 0 to 10 scale). Data is recorded in the Problem worksheet. You are going to assign between 8 to 12 people to each department. The problem is how to assign employees to workgroups to maximize total satisfaction and ensure that each division has the required number of employees.
- Solution: Solver Parameters are as follows:
  - Set Objective: P146
  - To: Max
  - By Changing Variable Cells: C140:C179
  - Subject to the Constraints: C140:C179<=4, C140:C179=integer, C140:C179>=1, Q141:Q144=0
  - Select a Solving Method: Evolutionary

The following image displays the solution to the first exercise.

Get FREE Advanced Excel Exercises with Solutions!