Method 1 – Calculating Minimum Number of Telephone Reservation Operators to Meet Labor Demands
Look at the dataset before explaining the situation.
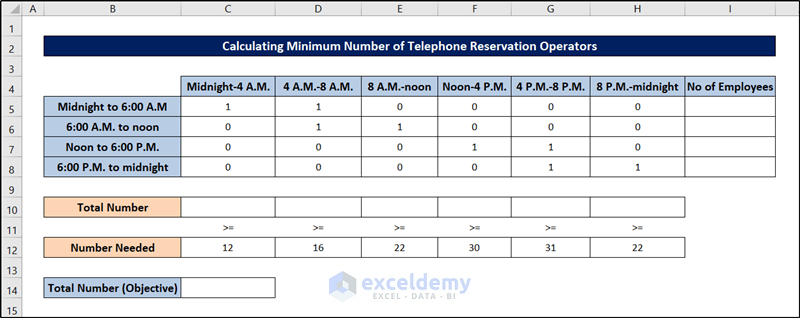
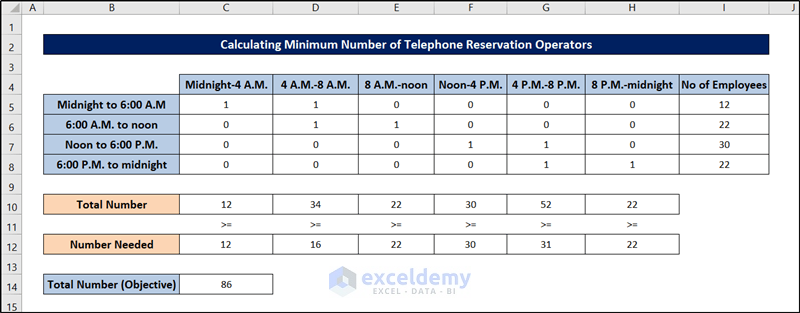
It shows the number of telephone reservation operators needed by an airline during each time of day. Each operator works one of the following six-hour shifts: midnight to 6:00 A.M, 6:00 A.M. to noon, noon to 6:00 P.M., and 6:00 P.M. to midnight. The minimum number of operators needed is shown in the range C12:H12.
Determine the objective, changing cells, and constraints of this problem.
Objective: Minimize the total number of employees
Changing cells: The number of employees working each six-hour shift.
Explicit Constraints: For each time of day, the number of employees who are working must be greater than or equal to the number of employees required
Implicit Constraints: Each changing cell must be a non-negative integer
To set up the model, information was put in the range C5:H8. The number of employees working each of those six-hour shifts will be filled into the range I5:I8. Since the numbers are unknown and need to be solved, we will leave them blank now.
We prepared the sheet by the usage of the SUM and SUMPRODUCT functions.
Follow these steps to prepare the dataset and optimize the schedule in Excel.
Steps:
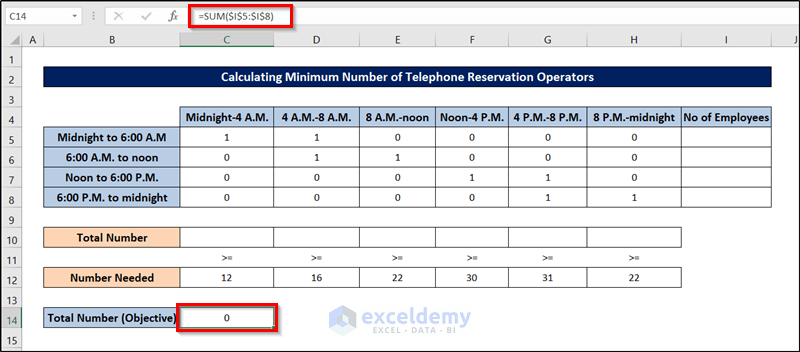
- Enter the following formula into cell C14 to calculate the total number of employees.
=SUM($I$5:$I$8)
- Press Enter.
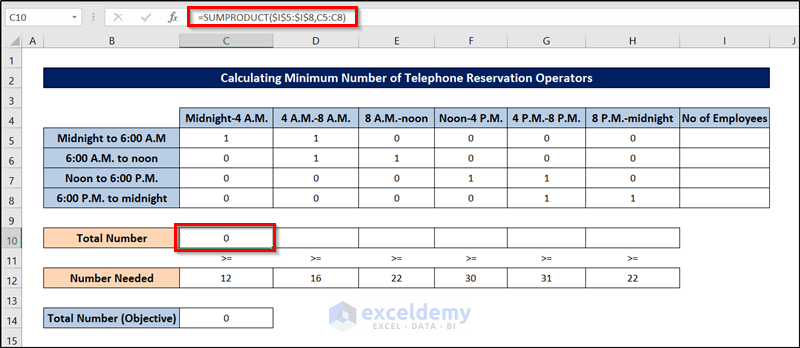
- Calculate the number of employees available from midnight to 4 A.M., and enter the following formula into cell D10.
=SUMPRODUCT($I$5:$I$8,C5:C8)
- Press Enter.
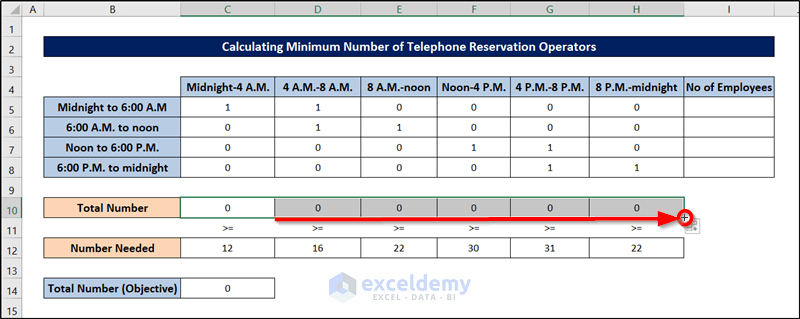
- Click and drag this to the right till cell H10 replicates the formula.
- Click on the Data tab and then click on Solver in the Analysis group to open the Solver Parameters dialog box.
- Fill in the Solver Parameters box with the essential information as shown in the following figure.
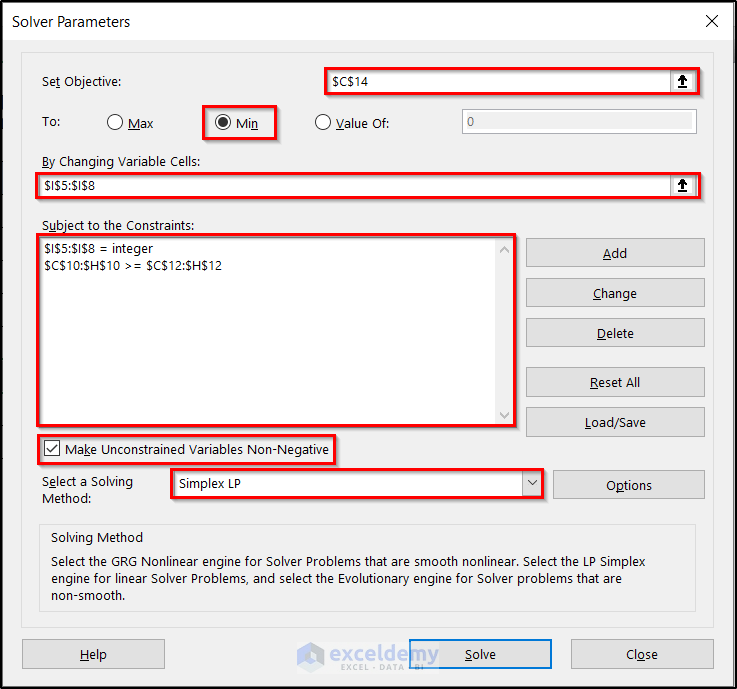
- Click Solve.
- A Solver Results box will appear like the following. Click OK.
The cells of the Excel spreadsheet will be filled out as follows, indicating the optimum number of operators required in this schedule optimization problem.
Method 2 – Calculating Minimum Number of Bank Employees to Meet Labor Demands
For solving this schedule optimization problem in Excel, we will use the following dataset.
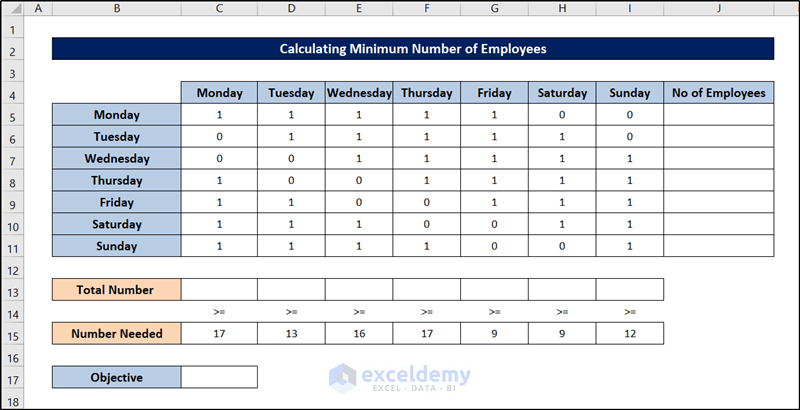
The number of workers needed for a bank is shown in cells from C15 through I15. 17 workers are needed on Monday, 13 workers are needed on Tuesday, 15 workers are needed on Wednesday, and so on. All bank employees work five consecutive days. What is the minimum number of employees can this bank have to meet its labor requirement?
The numbers of employees who start work (the first of five consecutive days) each day of the week will be recorded in the range J5:J11. The total number of employees – is put into cell C17. The range C5:I11 is used to track whether employees work or not. 1 means that the employee will work on that weekday, while 0 indicates that the employee will not work on that day. For example, 1 in C5:G5 means that employees start working on Monday and work Monday through Friday. We prepared the sheet by the usage of the SUM and SUMPRODUCT functions
Follow the steps to solve the schedule optimization problem in Excel.
Steps:
- To count the total number of employees who are working on Monday is filled into cell C13 by using the following formula.
=SUMPRODUCT($J$5:$J$11,C5:C11)
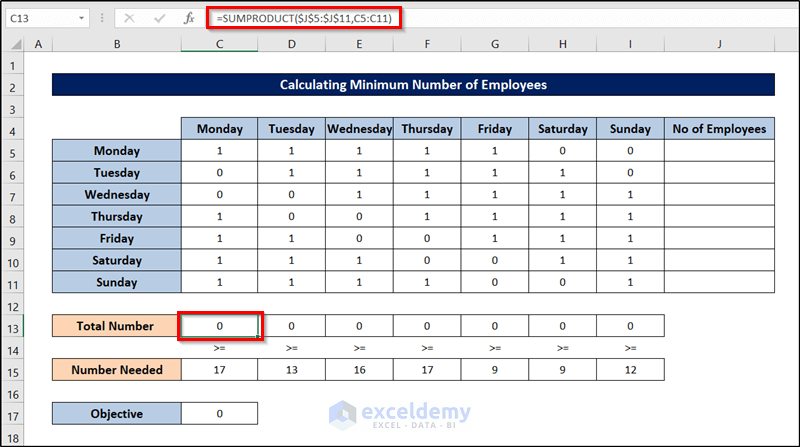
- Replicate it by clicking and dragging the fill handle icon to the right.
- Click on the Data tab and Solver in the Analysis group to open the Solver Parameters dialog box.
- Fill in the Solver Parameters box with the essential information shown in the following figure.
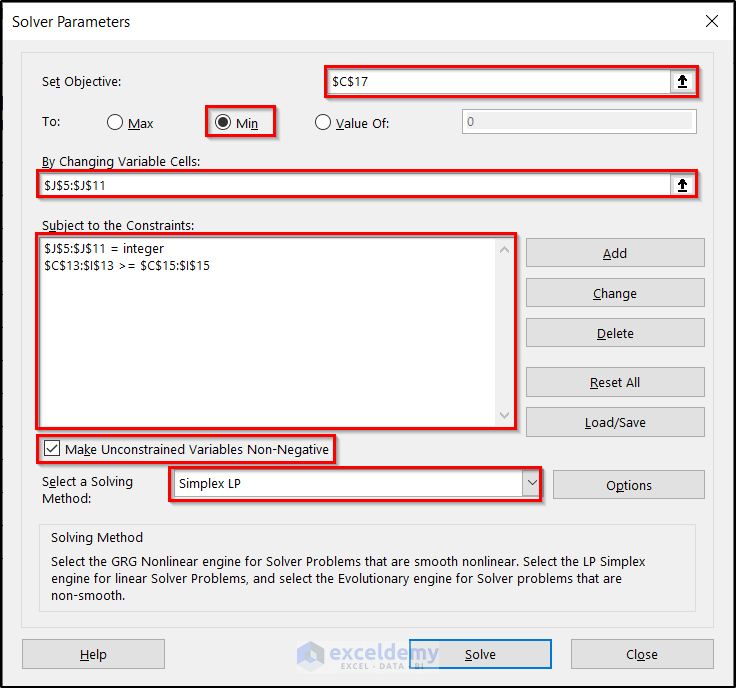
- Click Solve.
- A Solver Results box will appear like the following. Click OK.
The cells of the Excel spreadsheet will be filled out as follows, indicating the optimum number of employees required to meet labor demands in this schedule optimization problem.
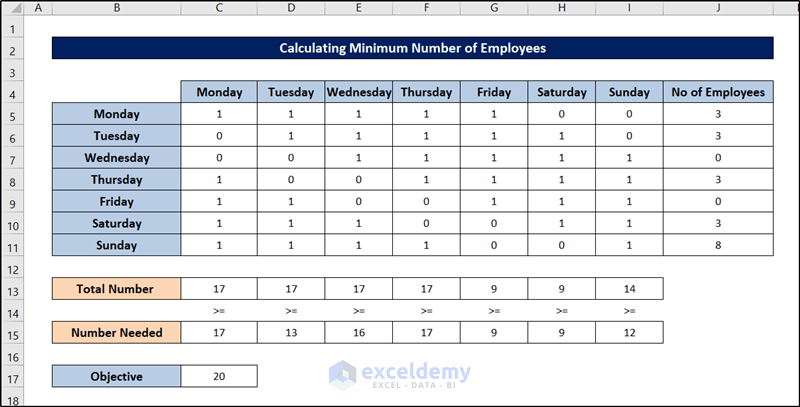
Method 3 – Minimizing Salary That Banks Should Pay Employees
If the employees in the same bank (in case 2) are paid $150 per day for the first five days, and they work a day of overtime at a cost of $350. How should the bank schedule its employees?
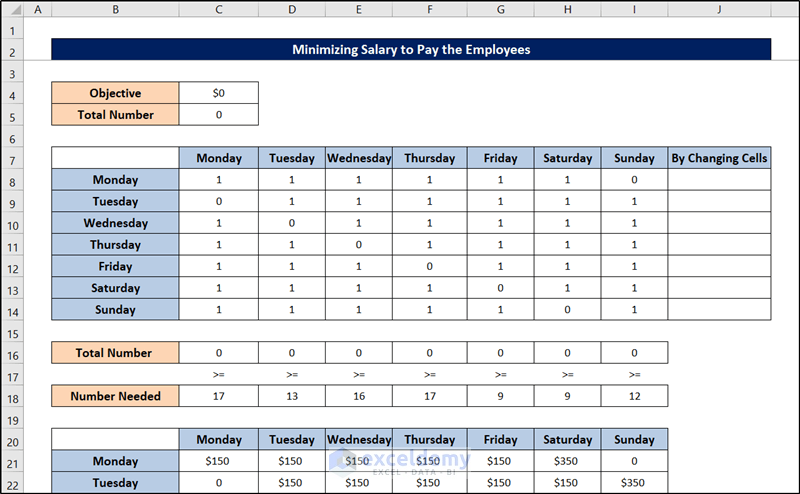
There are two parts to the dataset. The range C8:I14 provides information that can be used to compute constraints, while the range C21:I27 offers information for calculating how much the bank should pay its employees. In this case, are the same as those in case 2. And similar to case 2, we have prepared the sheet using the SUM and SUMPRODUCT functions.
Now we can follow these steps once we have the spreadsheet ready at our disposal.
Steps:
- Go to the Data tab on the ribbon.
- Select Solver from the Analyze group.
- Fill out the Solver Parameters box with the essential information in the figure below.
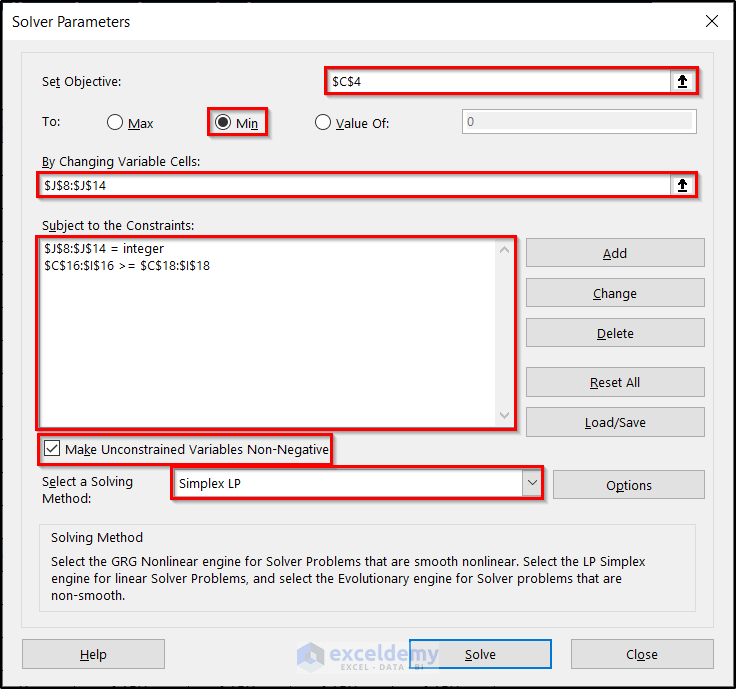
- Click on Solve.
- In the Solver Results box, click OK.
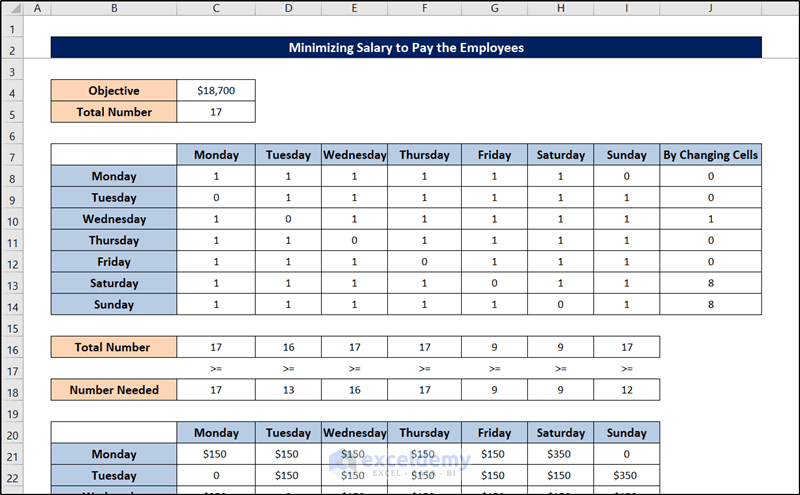
The cells of the Excel spreadsheet will get filled up like the following indicating the minimum salary the bank can pay employees in this schedule optimization problem.
Method 4 – Maximizing Number of Weekend Days Off with a Fixed Number of Employees
The bank has 22 employees. How should the workers be scheduled so that they would have the maximum number of weekend days off?
This spreadsheet has two parts too.
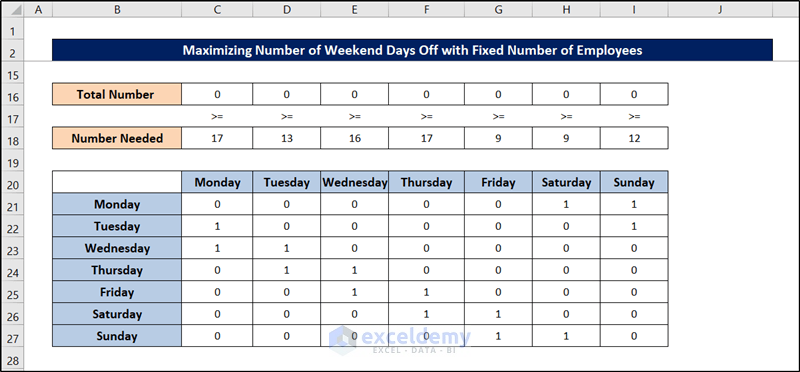
We prepared the sheet by the usage of the SUM and SUMPRODUCT functions. Once the sheet is prepared, you can follow these steps to tackle this schedule optimization problem in Excel.
Steps:
- Go to the Data tab on the ribbon.
- Select Solver from the Analyze
- The Solver Parameters box will appear. Now, fill out the Solver Parameters box with the essential information shown in the figure below.
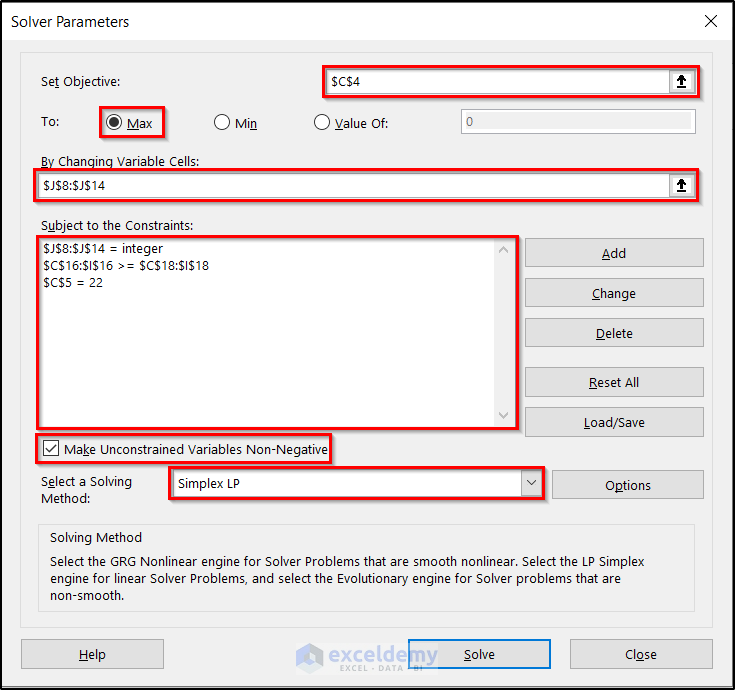
- Click on Solve.
- In the Solver Results box, click OK.
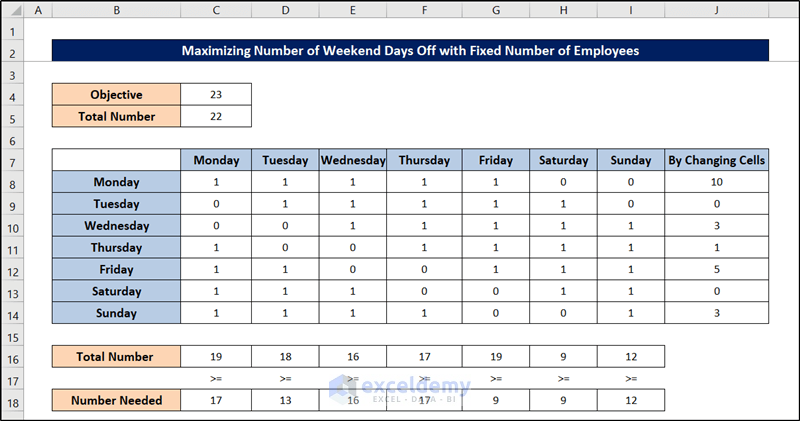
The Excel spreadsheet will get filled up like the following indicating the minimum number of weekend days off with a fixed number of employees in this schedule optimization problem.
Download the working file from the link below.
Related Articles
- How to Solve Linear Optimization Model in Excel
- How to Solve Network Optimization Model in Excel
- How to Calculate Optimal Product Mix in Excel
- Mean Variance Optimization in Excel
- Perform Multi-Objective Optimization with Excel Solver
<< Go Back to Optimization in Excel | Solver in Excel | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!
Thank you very much, Zhiping. Examples you provided refreshed my memory, which are helpful. Good work, much appreciated indeed.
Hi Peter,
Thank you.
Thank you for your effort in the examples you provided, they are clear and understandable……Are there any solved examples about distribution or transportation problem using solver?. I appreciate your response. Thank you very much.
Greetings, Huda.
I appreciate you asking this question. Solved examples are available about distribution or transportation problems. You can find it here “Solving Transportation or Distribution Problems using Excel Solver”.