Daily Compound Interest Formula in Excel
The basic compound interest formula is shown below:
n = Number of periods
Consider an investment of $1,000 for 5 years with an interest rate of 5% compounded monthly.
The monthly compound interest will be:

The daily compound interest will be:

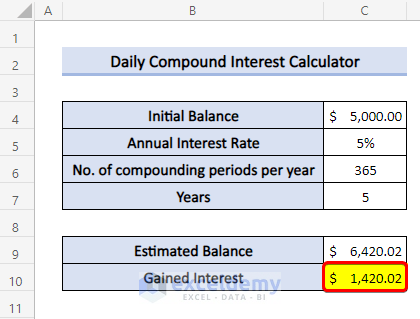
Step by Step Guide for Creating a Daily Compound Interest Calculator in Excel
Our dataset contains some basic information necessary to calculate the daily compound interest.
We are using this formula:
Steps
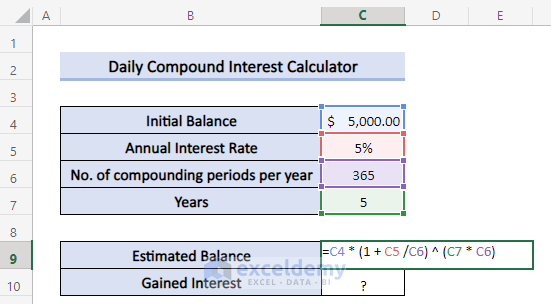
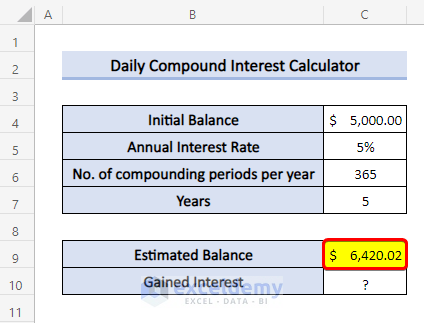
- Insert the following formula in cell C9:
=C4*(1+C5/C6)^(C7*C6)- Press Enter.
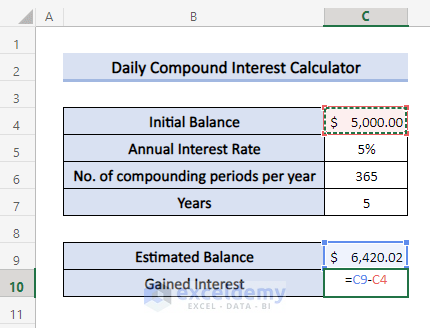
- To calculate the Gained Interest, use the following in cell C10:
=C9-C4- Press Enter.
Read More: Create Reverse Compound Interest Calculator in Excel
Test the Calculator for Daily, Monthly, and Yearly Compounding Periods: An Example
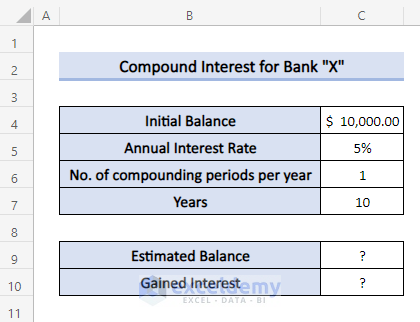
Suppose you want to invest $10000 for ten years somewhere. You have three options:
Bank "X" is providing 5% interest compounded yearly.Bank "Y"is offering 5% interest compounded monthly.Bank "Z" is giving 5% interest compounded daily.
Let’s use the calculator to find which one will provide you with most benefits.
Computing Yearly Compound Interest:
Here, we are using this dataset to demonstrate all the examples:
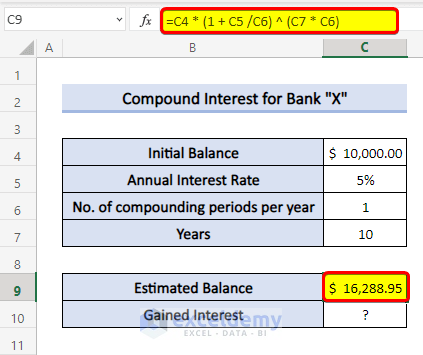
Steps
- Use the following formula in cell C9:
=C4*(1+C5/C6)^(C7*C6)- Press Enter.
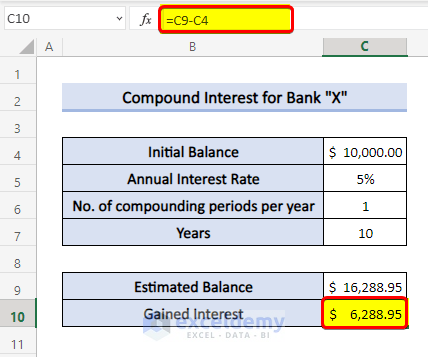
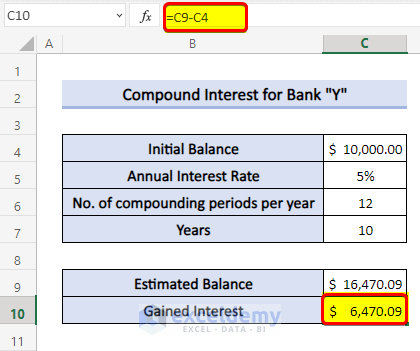
- To calculate the Gained Interest, use the following in Cell C10:
=C9-C4- Again, press Enter.
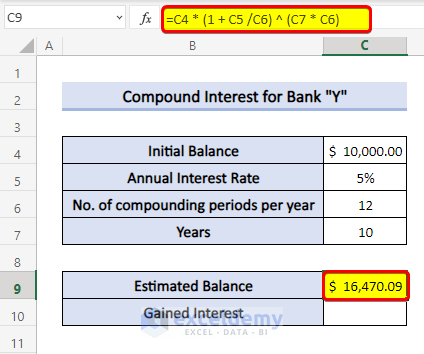
Computing Monthly Compound Interest:
Steps
- Use the following formula in Cell C9:
=C4*(1+C5/C6)^(C7*C6)- Press Enter.
- To calculate the Gained Interest, use the following in cell C10:
=C9-C4- Again, press Enter.
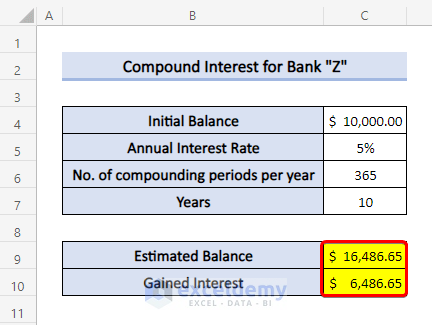
Computing Daily Compound Interest:
If we calculate interest for Bank “Z”, it will show the following:
Related Content: Make Quarterly Compound Interest Calculator in Excel
An Advanced Excel Function to Find the Compound Interest
Syntax:
=FV (rate, nper, pmt, [pv], [type])
Arguments:
rate: Required. The interest rate for each period.
nper: Required. The number of compounding periods.
pmt: Required. The additional payment per period, and is represented as a negative number. If there is no value for “pmt,” put a value of zero.
pv: Optional. The principal investment, which is also represented as a negative number. If there is no value for “pv,” you must include a value for “pmt.”
type: Optional. Indicates when additional payments occur. “0” indicates that the payments occur at the beginning of the period, and “1” indicates that the payments are due at the end of the period.
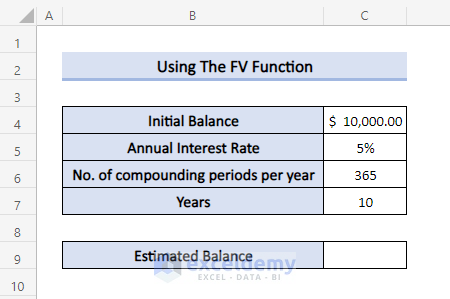
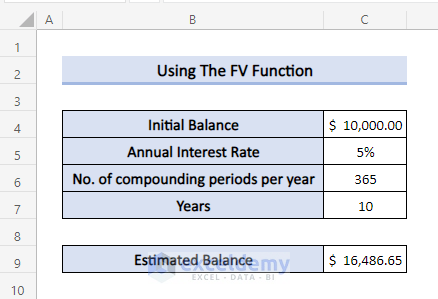
We’ll use the same simple dataset.
Steps
- Use the following formula in Cell C9:
=FV(C5/C6,C7*C6,0,-C4)To acquire the rate (which is the period rate) we use the annual rate/periods or C5/C6.
To get the number of periods (nper), we use the (term * periods) or C7 * C6.
There is no periodic payment, so we use zero.
The current value (pv) is input as a negative value, since the $10,000 “leaves your wallet” and belongs to the bank during the period.
- Press Enter.
Download the Template
Related Articles
- Create a Daily Loan Interest Calculator in Excel
- Bank Interest Calculator in Excel Sheet – Download Free Template
- How to Develop CD Interest Calculator in Excel
- How to Create SIP Interest Calculator in Excel
- How to Generate Overdraft Interest Calculator in Excel
<< Go Back to Finance Template | Excel Templates
Get FREE Advanced Excel Exercises with Solutions!




Everything you have here makes sense, but what if the loan doesn’t have a specific term? It gets paid off whenever it gets paid off.
Hi Laurie!
It feels good to know that you found our content understandable. Judging from you query, I think you want a continuing compound interest formula where the loan doesn’t have a specific term/year.
The term continuous compound interest is used to emphasize the continuous compounding of interest, as opposed to discrete compounding periods. Here, the compounding frequency becomes infinite, resulting in a continuous growth formula. Let us look at the formula below:
A=P0ert
Where,
For example, if you invest $1,000 at an annual interest rate of 5% continuously compounded for 2 years, the future value can be calculated using the continuous compounding formula.
Regards,
Nafis
ExcelDemy