What Are Coordinates (Northing and Easting)?
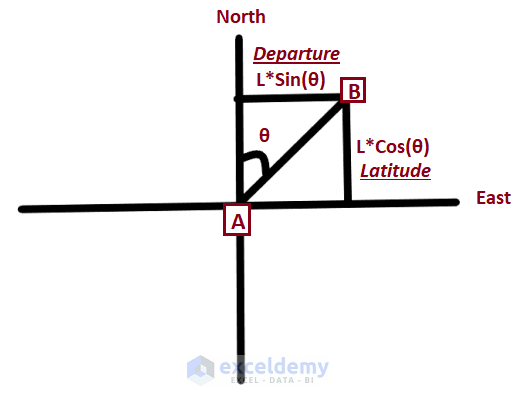
The geographic Cartesian Coordinates of a point on earth are referred to as Easting (the x value), and Northing (the Y value). The distance (L) is known as the Orthogonal Coordinate measured from a horizontal datum. We use the method of Latitude and Departure to determine the Northing and Easting, thus calculating the Coordinates.
To calculate coordinates, you need to have the source data such as the bearing and distance of lines connecting two or multiple points. As Excel only takes bearings in Radians, you should first convert the bearing readings into radians.
For illustration, we have a sample dataset with a reference point (i.e., New York City coordinate). From the reference point, we have multiple points maintaining intervals of certain distances. We will calculate the coordinates of those points using the Latitude and Departure methods.
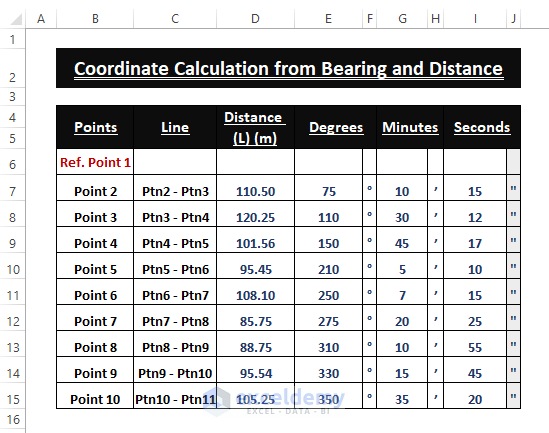
Step 1 – Setting Up Bearings and Distances
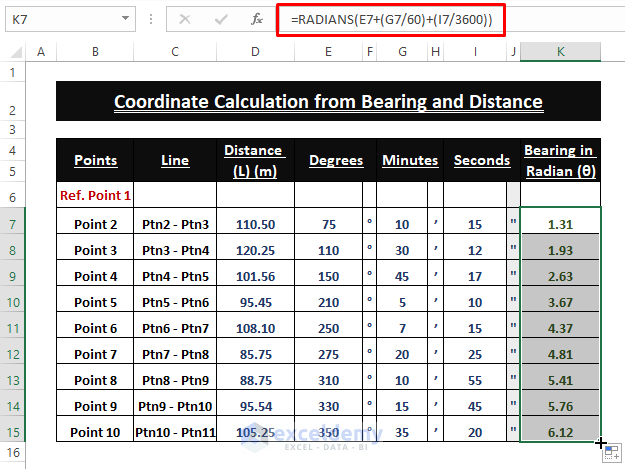
Arrange the given bearing (i.e., Degrees, Minutes, Seconds) and distance readings in an organized manner in Excel Worksheet. Provide clear labels for the data, along with their units (i.e., Meter or Degree, Minute, Second), as shown in the image below.
Step 2 – Bearing Conversion in Radian
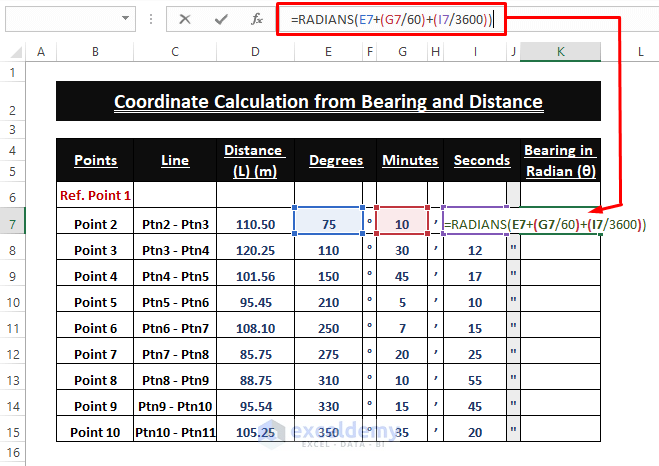
➤ Use the formula below to convert Degrees, Minutes, and Seconds into Radians.
=RADIANS(E7+(G7/60)+(I7/3600))In the formula, G7/60 converts the Minutes into Degrees, I7/3600 the Seconds into Degrees, and the RADIANS function converts the Degree values into Radians.
➤ Drag the Fill Handle to apply the formula to other cells.
Step 3 – Finding Latitude and Departure
Additional Latitude
The Latitude is the product of the Cosine value of the Bearing and the Distance (L).
➤ Add the following COS function in cell L7.
=D7*COS(K7)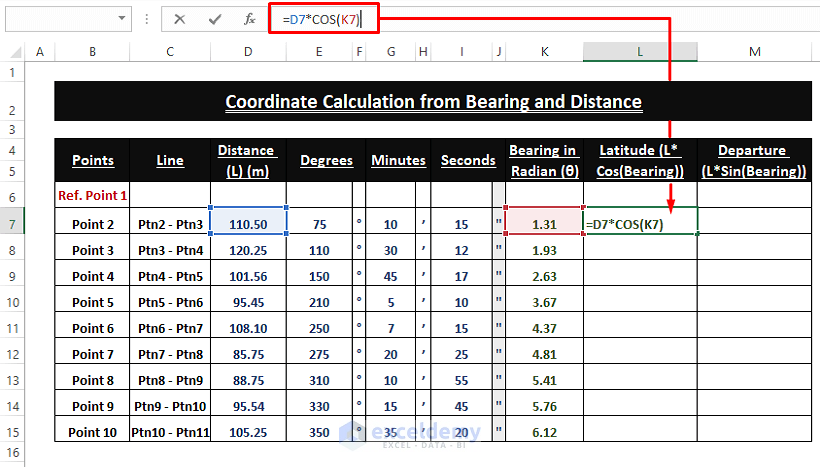
➤ Drag the Fill Handle to execute the formula in the other cells.
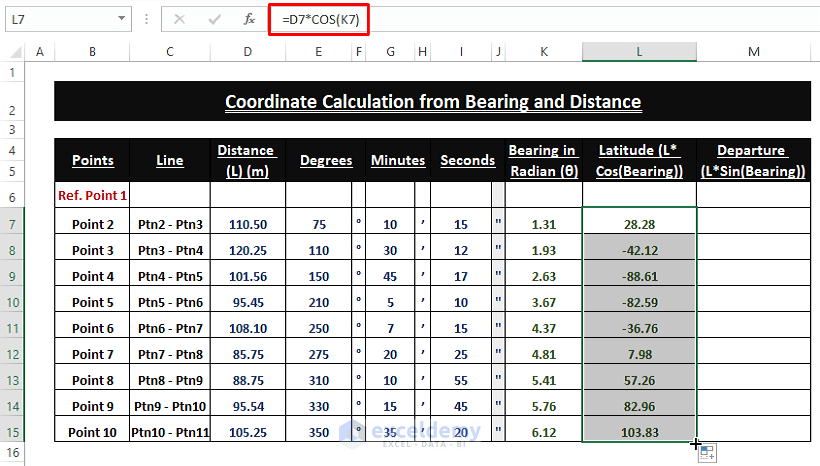
You will get the additional Latitude from the reference point (i.e., New York City).
Additional Departure
Departure is the horizontal distance from a reference point.
Departure is the product of the Sine value and Distance.
➤ Add the following formula in any blank cell (i.e., M7)
=D7*SIN(K7)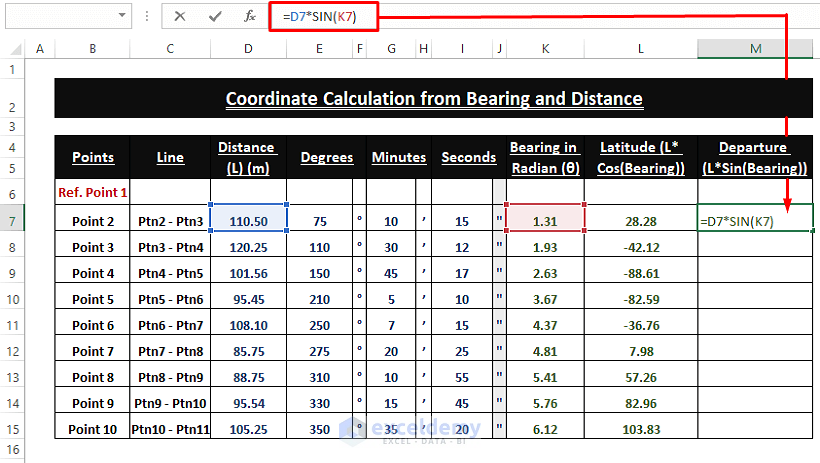
➤ Apply the Fill Handle to display the Departure values in all the other cells.
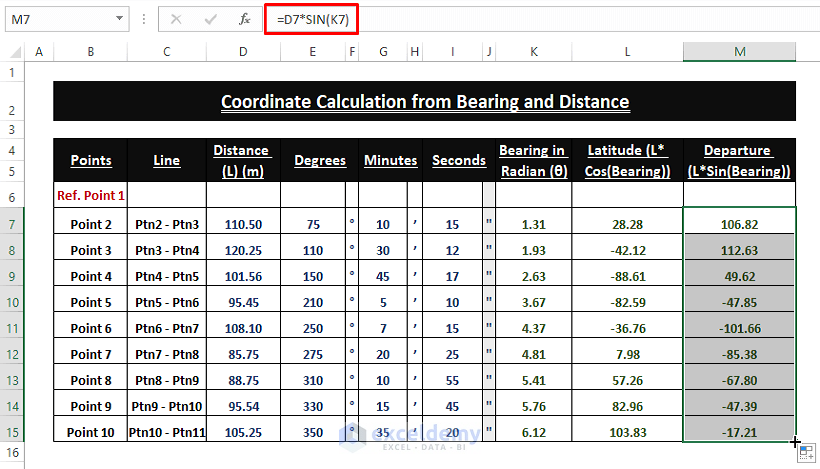
Step 4 – Calculating Coordinates from Bearing and Distance
Users need a reference point (i.e., New York City Coordinates) to measure the coordinates of regular intervals and bearings. There is a reference Coordinates in the dataset and users have to add each additional Latitude and Departure to find the respective Northing and Easting.
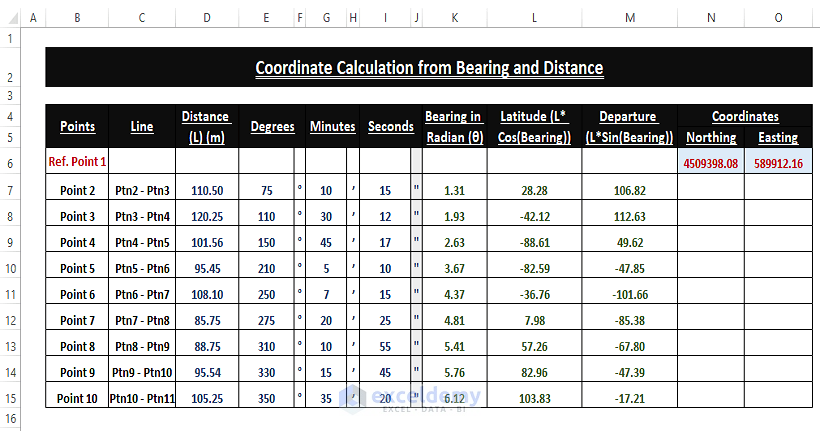
Point Northing
➤ Add the additional Latitude to the reference Northing to find the final Northing of any point.
=L7+N6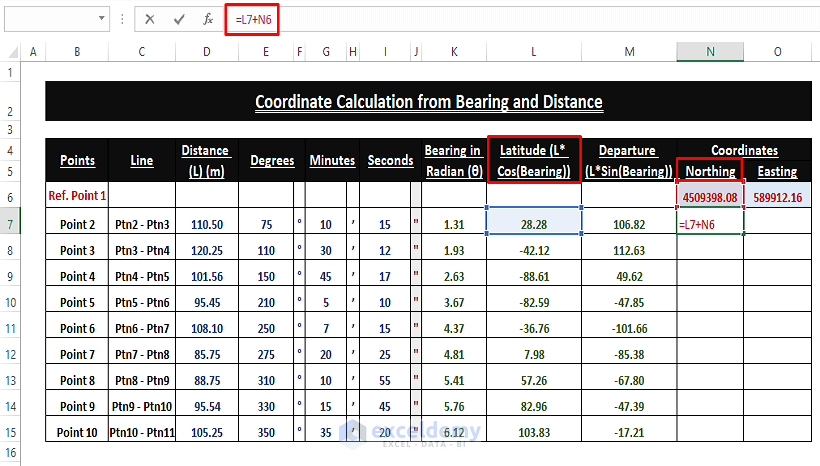
➤ Drag the Fill Handle to display the Northing Coordinate values in all cells.
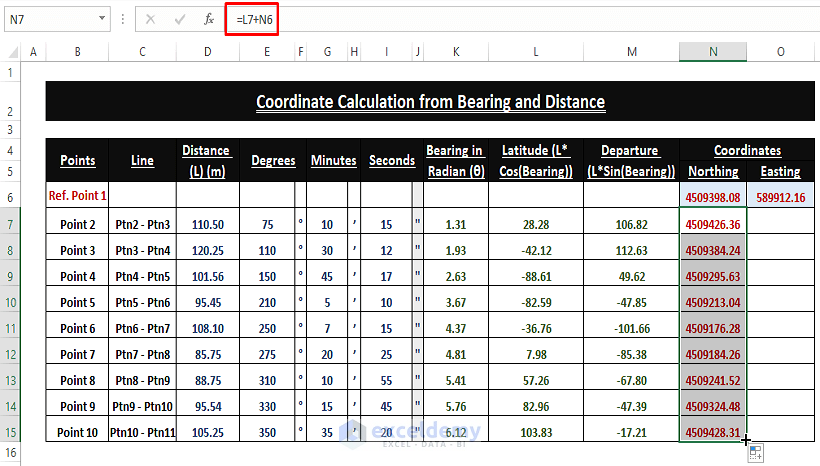
Point Easting
➤ Use the Addition Operator to find the final Easting of any point.
=M7+O6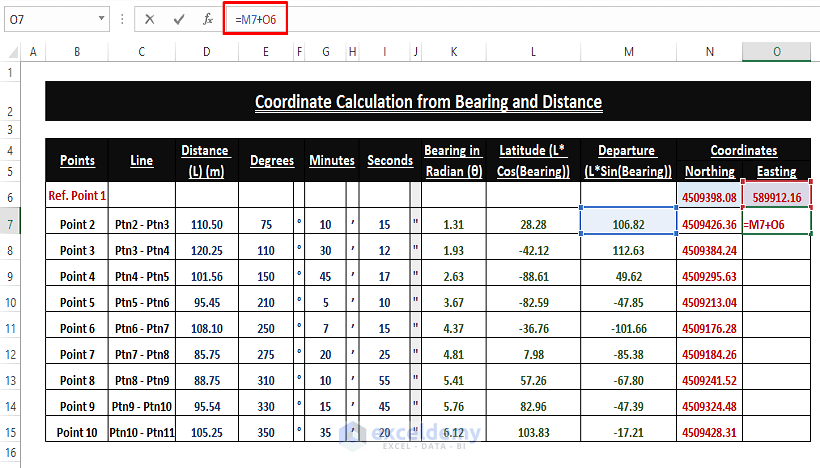
➤ Drag the Fill Handle to execute the addition operator in other cells.
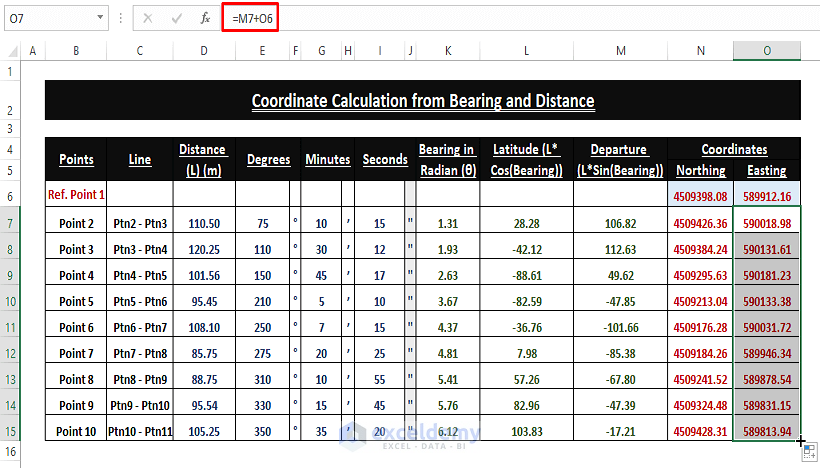
You’ll get the Coordinates from bearing and distance.
Download Excel Workbook
<< Go Back to Distance | Formula List | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!


Thanks! Very helpful
Welcome @Janice
How do you factor in the East or West of the bearing – does this need to be accounted for? For example, should 19 degrees East be positive radians whereas if it were West, it would be negative Radians – or am I not understanding something. I am trying to use this process on a set of legal descriptions, and so far, it’s not aligning with a known map.
Hello Hannah!
Thanks for reaching out! You are correct. The direction (East or West) of the bearing is crucial, and it needs to be accounted for in the calculation of radians.
In navigation and mapping, the convention is usually to measure bearings clockwise from north, meaning that eastward directions are considered positive, and westward directions are considered negative. Bearings can be given in degrees, minutes, and seconds or in radians. To account for this, you should modify the formula for converting bearings to radians as follows:
For East Bearings: Simply convert degrees, minutes, and seconds to radians as previously described, and the result will be positive.
=RADIANS(Degrees + (Minutes / 60) + (Seconds / 3600))
For West Bearings: Convert degrees, minutes, and seconds to radians as previously described, but make the result negative.
=-RADIANS(Degrees + (Minutes / 60) + (Seconds / 3600))
By introducing the negative sign for West bearings, you account for the direction correctly. Positive radians represent East bearings, and negative radians represent West bearings.
Please keep in mind,
Bearings measured clockwise from true north: East is positive. West is negative.
Bearings measured in radians: Counterclockwise is positive. Clockwise is negative.
If you have any further queries, please inform us in the reply section. Thanks.
Best Regards,
ExcelDemy Team
hello, can you explain how to modify formula if have southerly direcctions in the bearings. thank you
Dear, Thanks for visiting our blog and sharing your questions. You want to modify the existing formula to deal with the southerly direction of the bearings. The provided formulas in the article work for any bearing, regardless of direction. This is because the SIN and COS functions account for the direction within their calculations.
Southerly bearings typically range from 180 to 270 degrees. The formulas will handle these values fine and automatically calculate the appropriate change in Northing and Easting based on the southerly direction. The cosine value for bearings in this range will be negative, meaning there will be a decrease in Northing because the reference point is likely north of the new point. Likewise, the sine value will be positive, meaning an increase in Easting because a southerly direction moves the point eastward.
So, you don’t need to modify the formulas for southerly directions. They will work as intended.
Regards
Lutfor Rahman Shimanto
ExcelDemy