Calculus is an important part of mathematics. We may have to perform several calculus operations for practical analysis. Even though there are no Excel functions dedicated to Calculus operation, we can find the Differentiation and Integration in an Excel worksheet.
In this article, we will show how to perform Differentiation and Integration in Excel. We will calculate Differentiation and Integration by manual formula. Also, we are going to use the Formula with finite difference method for finding derivatives. On the other hand, we will also find the area under a curve by Integration.
Also, we will show how to calculate average velocity by the SLOPE function.
Download Practice Workbook
What are the Ways to Calculate Differentiation in Excel?
There are two ways to calculate Differentiation in Excel. We can do so manually (mathematical calculation) or by using a generic Excel formula with functions.
1. How to Calculate Differentiation Manually in Excel?
We can calculate the differentiation manually with some easy steps.
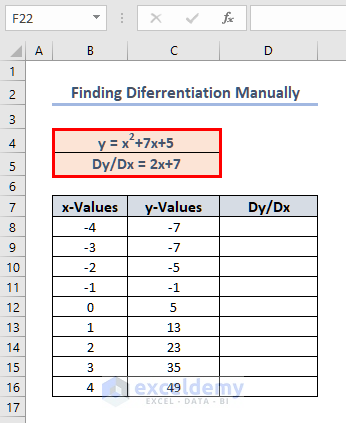
- First, set the differentiation equation.
y= x2+7x+5Dy/Dx = 2x+7- Then, use the differentiation result as a reference formula.
- We have taken several x-values and their corresponding y-values. As we have the differential formula for our equation, we can find differentiation at every x-value.
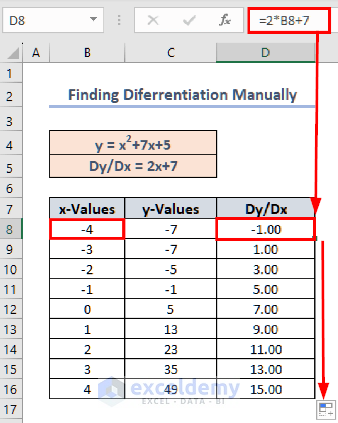
- To find the differentiation, write the following formula in D8 and press ENTER.
=2*B8+7- We got differentiation for the first point which is -1.
- Now, hold and drag the D8 cell downwards to find differentiation for all points.
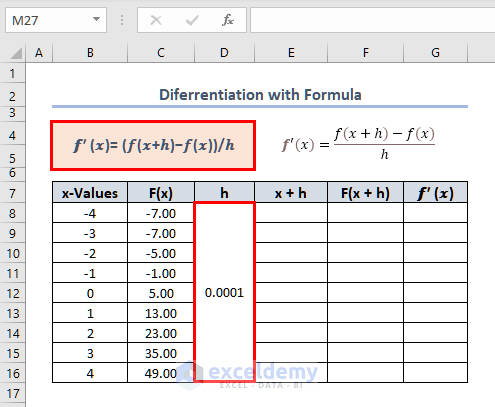
2. Can We Find Differentiation by Formula?
Yes, we can use a basic differential formula of finite difference to find Differentiation. The finite difference formula is given as:
f’(x)= {f(x+h)-f(x)}/hIn this method, we are going to set the value of h and find f(x+h) and f(x). And, from these values, we will find the differentiation f’(x). We have set the value of h as 0.0001.
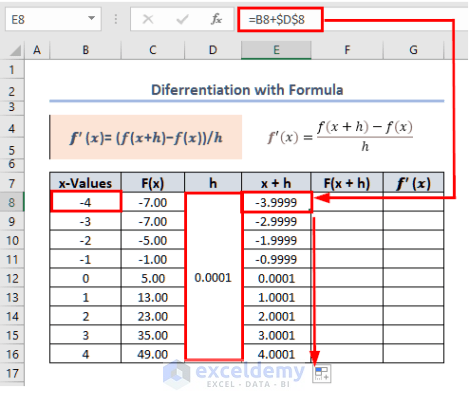
- Write the following formula in E8 to find the value of x+h.
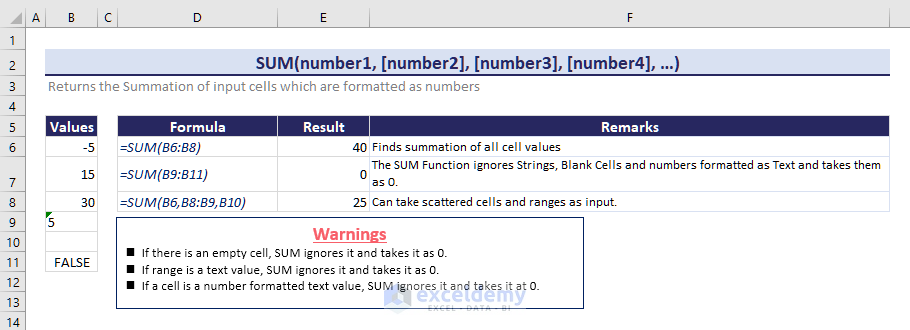
We can find Integration manually in Excel. Also, we can find the Area of a surface using the Trapezoidal formula. To calculate Integration manually, first, we have to find the Integration result. Then, we will insert that reference formula in the Excel sheet. The integration of the equation is given as: To find the Area under a curve, we can use the Trapezoidal integration formula. Let’s find the Area under the same equation from the x-values of -2.5 to 2.5. For this procedure, we will use the trapezoidal area rule. And, for accurate values, we have to set the x-value interval as low as possible. We will find the areas of each interval and then we can sum all those interval areas to get the total area. Click the image for a detailed view Yes. With the SLOPE function, we can determine the average slope or derivative of a given dataset. The overview of the SLOPE function is given in the following image: Click the image for a detailed view Let’s find the average velocity with this in-built function. Answer: Yes. You can insert the linear or exponential formulas, their derivatives, integrals, etc. in an Excel graph. Navigate to the Insert tab and select a suitable Area, Line, or any other chart to show your differentiation or integration values. Plotting the calculus results will visualize your results in a meaningful way. Answer: You can use Excel to solve simple Calculus problems. To find derivatives, you can use the SLOPE function. However, MS Excel doesn’t have any dedicated functions to solve complex calculus equations. Answer: We can use calculus to find velocity, acceleration, or data trends with differentiation. Also, we can find the area under a curve or the volume of an object by integration. We have shown you how to perform Calculus in Excel. As there is no dedicated Excel function, we had to find differentiation and integration manually. To find basic differentiation and integration, first, we had to find the generic formula manually. Then, we used Excel to find their values for different X-values. Also, we used the finite difference formula to find derivatives. We also showed you how to find the area under the curve using basic Excel tricks. We hope you find the content of this article useful. If there are more queries or suggestions, feel free to mention them in the comment section. << Go Back to | Excel for Math | Learn Excel=B8+$D$8
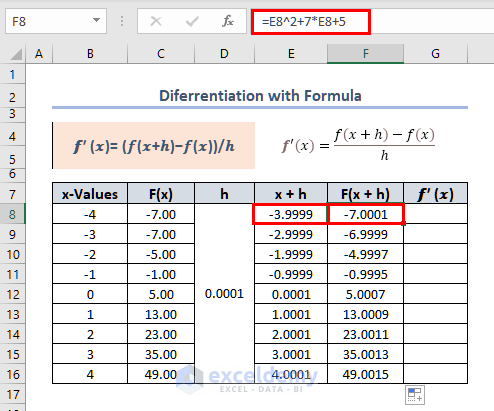
=E8^2+7*E8+5
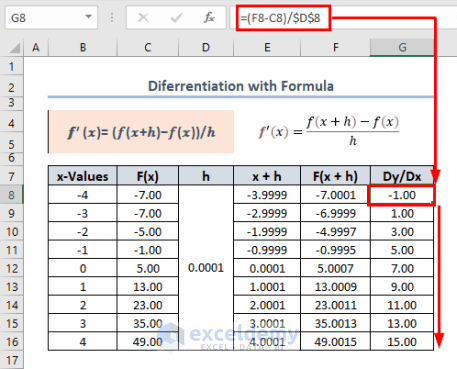
=(F8-C8)/$D$8
What are the Ways to Find Integration in Excel?
1. How Can You Calculate Integration Manually?
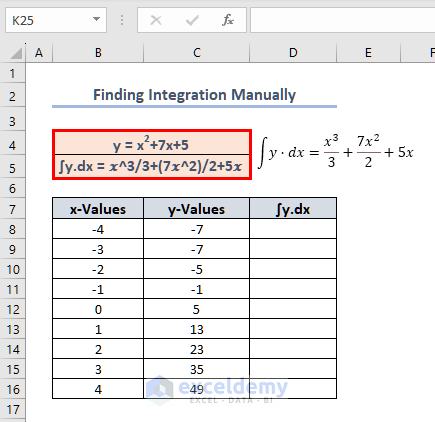
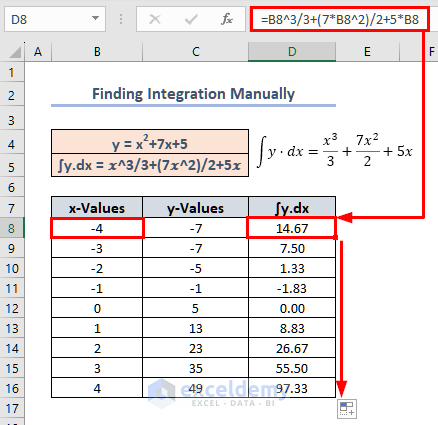
=B8^3/3+(7*B8^2)/2+5*B8
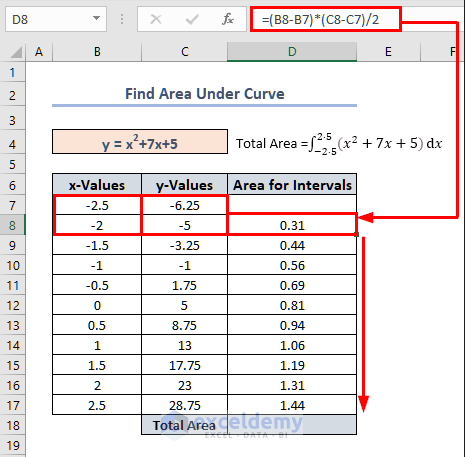
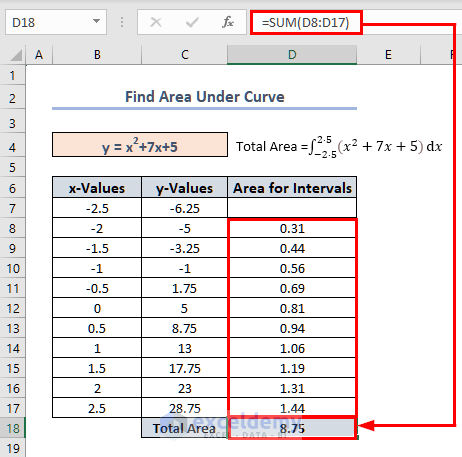
2. How Can We Find the Area under the Curve with Integration?
=(B8-B7)*(C8-C7)/2
=SUM(D8:D17)
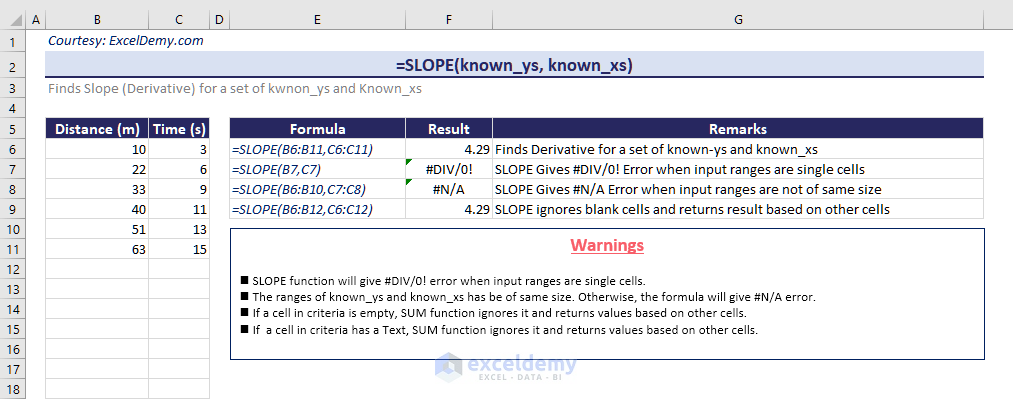
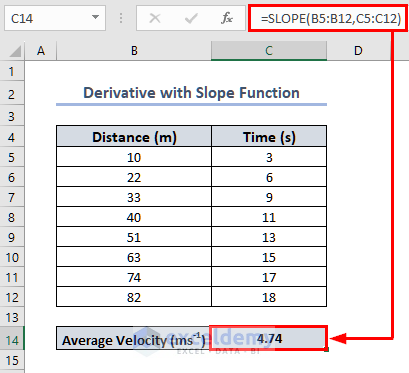
Can You Find a Derivative with the SLOPE function?
=SLOPE(B5:B12,C5:C12)
Which Things Should You Remember?
Frequently Asked Questions
1. Can I Graph Calculus Formulas in Excel?
2. Are there any Limitations to Using Calculus in Excel?
3. What can I Use Calculus for?
Conclusion
Calculus in Excel: Knowledge Hub
