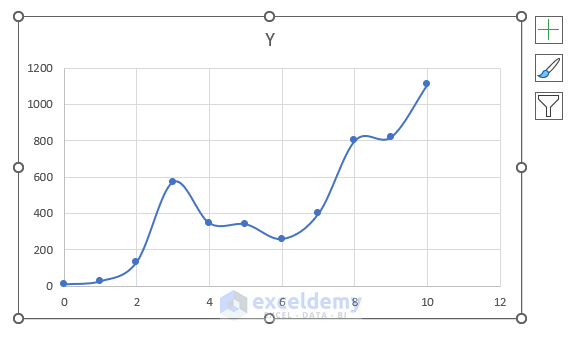
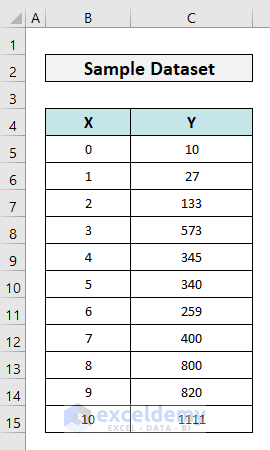
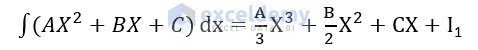How to Use Integration in Excel to Find Area Under a Curve

Posted on by Masum Mahdy

The following dataset shows some coordinates of a random curve.

Sample Dataset to create a curve and then calculate area under it using integration in Excel.

Step 1 – Set Data Properly and Create Scatter Chart

  • Set your data in order and select any cell of your data. Go to the Insert tab and from the Charts group, select a suitable chart type.
  • We have selected the Scatter with Smooth Lines and Markers option.

creating a scatter chart

  • The scatter chart will be inserted.

a curve

Step 2 – Enable Trendline and Its Equation

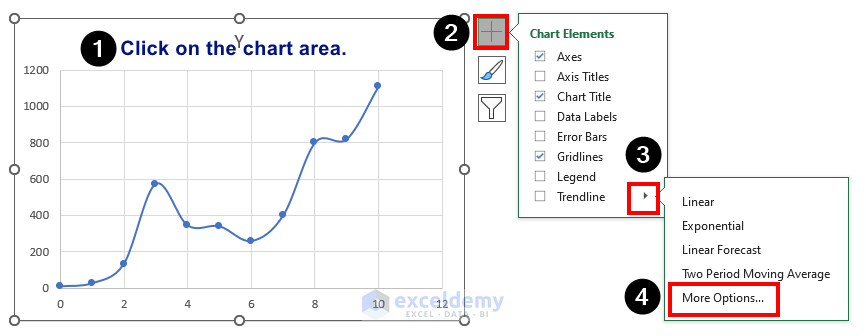
  • Click on the Chart Area.
  • Click the Chart Elements button.
  • From the Trendline dropdown, select More Options.

creating trendline in Excel

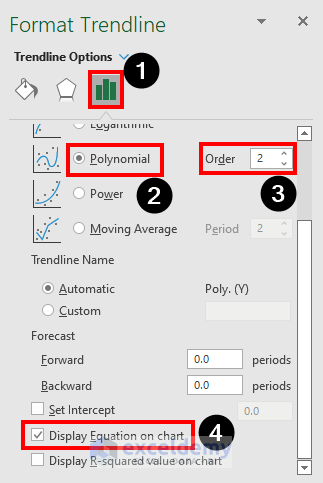
The Format Trendline window will appear.

  • Click on the Polynomial  and check the Display Equation on chart checkbox.

displaying trendline

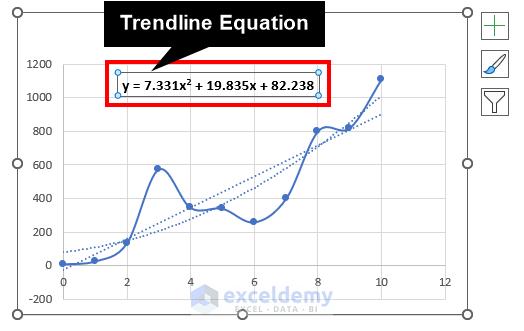
The following trendline equation will appear on the chart area.

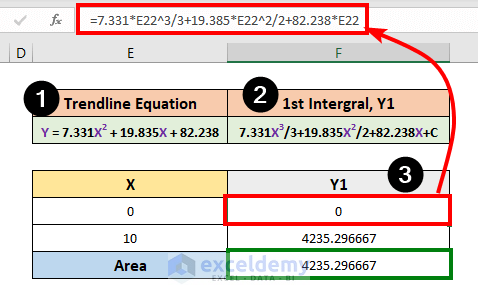
Y = 7.331X2 + 19.835X + 82.238

trendline equation to calculate area under curve using integration

Step 3 – Find the First Integral and Calculate Area Under Curve

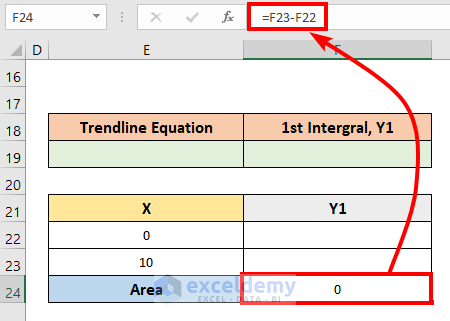
  • Create a table and insert the following formula in cell F24.
=F23-F22

  • Copy the trendline equation and paste it into cell E19.
  • Calculate the first integral with this equation using the following formula.

The first integral of Y is-

Y1 = 7.331X3/3 + 19.835X2/2 + 82.238X+C

  • Enter the following formula (or match it with your data) in cell F22 and copy it with the fill handle in cell F23.
=7.331*E22^3/3+19.385*E22^2/2+82.238*E22
  • The area is calculated in cell E24.

Calculate area under a curve using integration in Excel

Note:

The area under the curve is with respect to the X-axis. If you want to find the area under the curve with respect to the Y axis, flip the data horizontally, switch the axes and apply all the steps described.

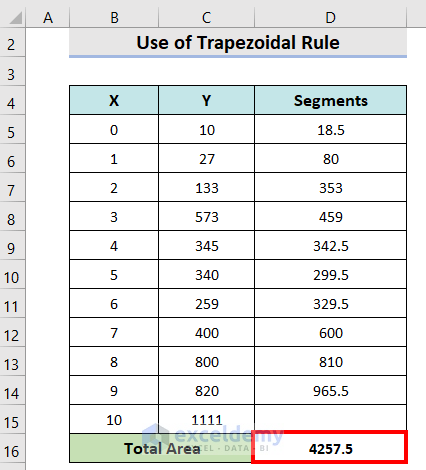
How to Calculate Area Under Curve in Excel Using Trapezoidal Rule

Steps:

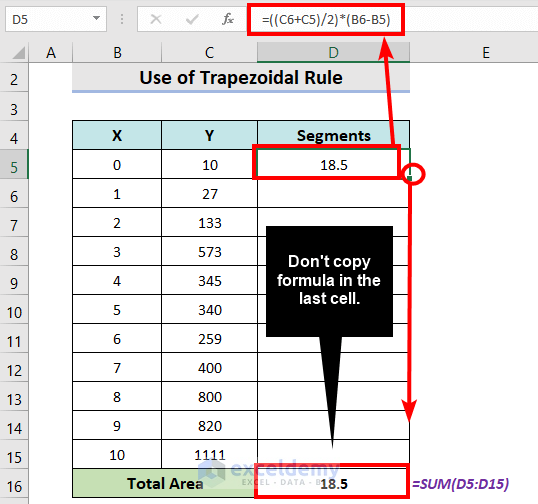
  • Insert the following formula in cell D5 and press Enter.
=((C6+C5)/2)*(B6-B5)
  • Drag the fill handle icon to cell D14. Leave the last as it is.
  • Insert the following formula in cell D16.
=SUM(D5:D15)
  • Press Enter.

Calculate area under a curve in Excel using trapezoidal rule.

  • It will output the value of area under curve.

Note:

More coordinates in the same range with smaller intervals will give a more accurate result.

Download Practice Workbook

<< Go Back to | Calculus in Excel | Excel for Math | Learn Excel

Get FREE Advanced Excel Exercises with Solutions!

Leave a Reply

Your email address will not be published. Required fields are marked *

Advanced Excel Exercises with Solutions PDF