Introduction to Integration in Excel
As there is no direct way to find the integral of a function in Excel, we will use the concept of Numerical Integration. Numerical Integration is basically a method that approximates the integral of a function by using some numerical approaches. In Excel, we can calculate integrals by following the 2 methods.
- Trapezoidal Method
- Midpoint Rule
What Is Trapezoidal Integration?
Trapezoidal Integration evaluates the area under a curve to find the integral of a function within a definite limit. In this method, the area under a curve is divided into very small trapezoids. By summing all the small trapezoids under the curve, we can calculate the total area under the curve, which is the integral value of the function.
Trapezoidal Integration Formula
Let’s say we have a function f(x) with limits p and q.
∫qp f(x) dx
To approximate the integral of the function f(x) by the Trapezoidal Method, we will use the following formula.
∫qp f(x) dx=(q-p)*(f(p)+f(q))/2
How to Do Trapezoidal Integration in Excel – 3 Methods
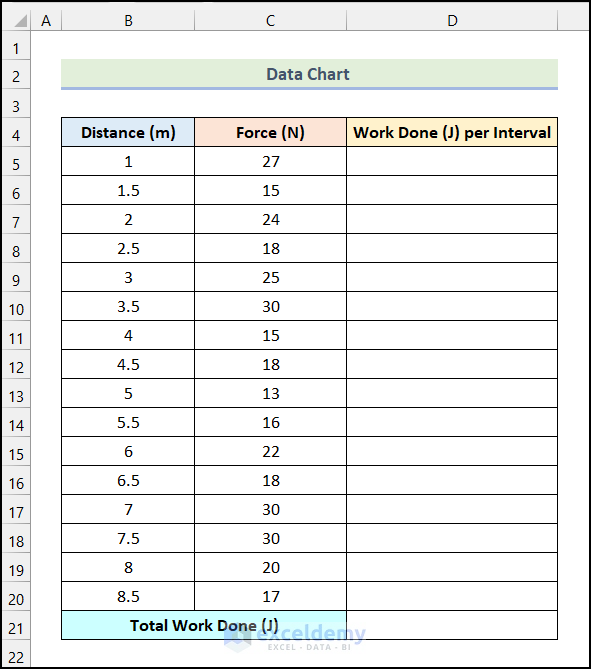
Let’s say we have a Data Chart for Distance (m) covered by the exertion of Force (N). The amount of Work Done (J) will be:
Work Done = Distance Covered * Applied Force
We will use the Trapezoidal Integration approach to approximate the Total Work Done (J).
Method 1 – Using a Mathematical Formula
Steps:
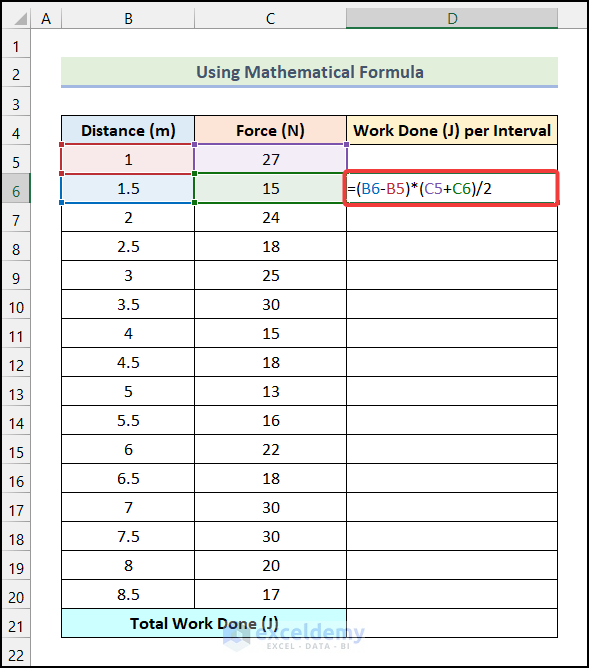
- Use the following formula in cell D6.
=(B6-B5)*(C5+C6)/2Cell B5 and cell B6 refer to the 1st and 2nd cells of the Distance (m) column respectively. Cells C5 and C6 indicate the 1st and 2nd cells of the Force (N) column.
- Press Enter.
Note: Here, each cell of the Work Done (J) per Interval column represents a small trapezoid. After adding all the areas together, we will find the value of the integral.
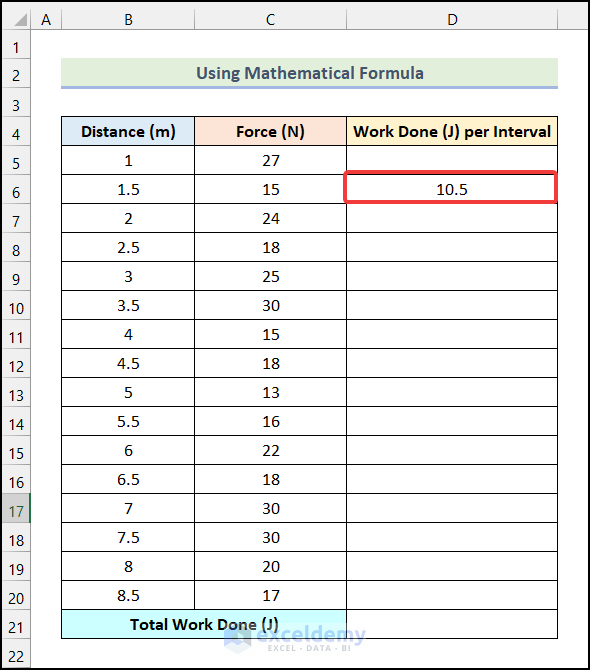
- You will have the Work Done (J) for the 1st interval.
- Drag the Fill Handle up to cell D20 to get the remaining outputs.
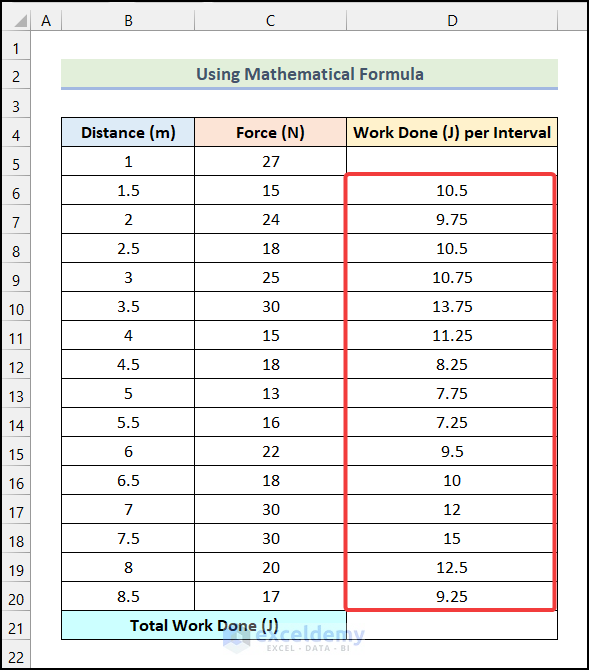
- Use the following formula in cell D21.
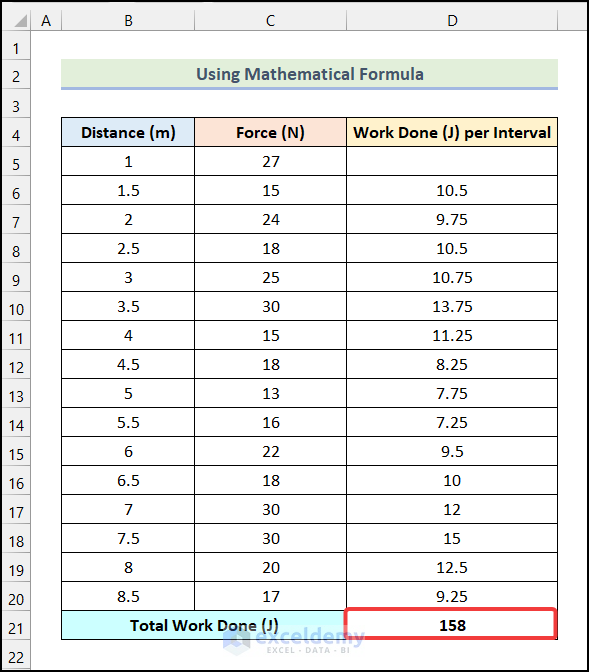
=SUM(D6:D20)The range D6:D20 indicates the cells of the Work Done (J) per Interval column, and the SUM function will return the summation of the values of range D6:D20.
- Hit Enter.
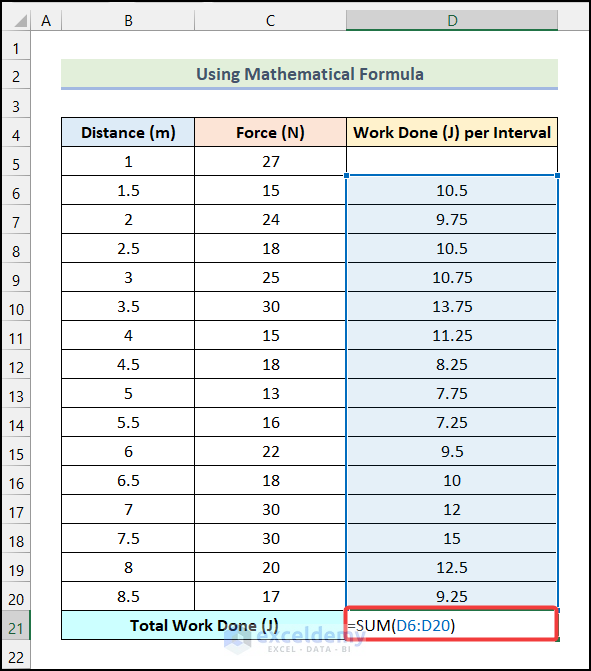
- You will have the Total Work Done (J) as shown in the following image.
Method 2 – Applying the SUMPRODUCT Function
Steps:
- Use the following formula in cell D5.
=SUMPRODUCT(B6:B20-B5:B19,(C6:C20+C5:C19)/2)Here, the range B6:B20 indicates the cells of the Distance (m) column, and the range C6:C20 refers to the cells of the Force (N) column.
- Press Enter.
Formula Breakdown
- B6:B20-B5:B19 is the array1 argument.
- We subtracted array B5:B19 from the array B6:B20.
- This indicates the 1st part of the Trapezoid Integration formula (b-a).
- (C6:C20+C5:C19)/2 is the [array2] argument.
- Here, we added the array C6:C20 and C5:C19, then divided them by 2.
- It indicates the 2nd part of the Trapezoid Integration formula (f(p)+f(q)2).
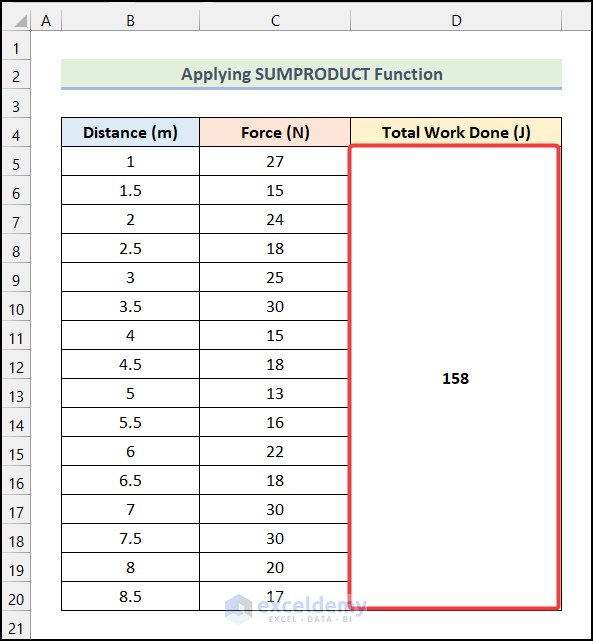
- Output → 158.
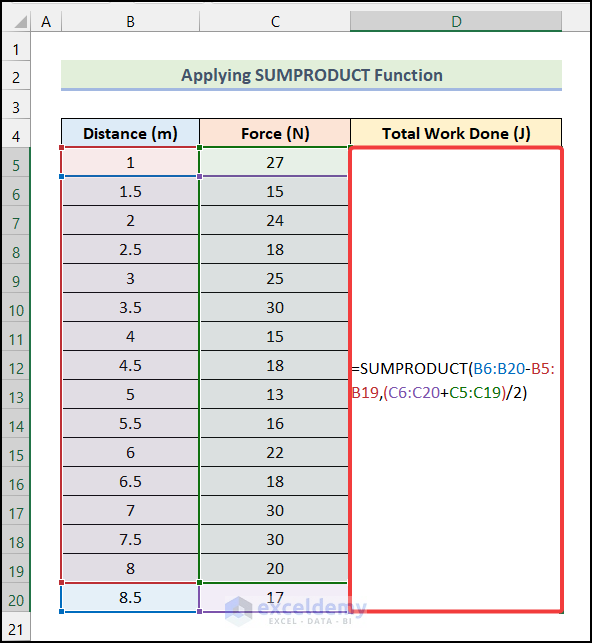
- You will have the Total Work Done (J) in cell D5 as demonstrated in the following picture.
Method 3 – Utilizing VBA Macro
Steps:
- Go to the Developer tab from Ribbon.
- Click on the Visual Basic option from the Code group.
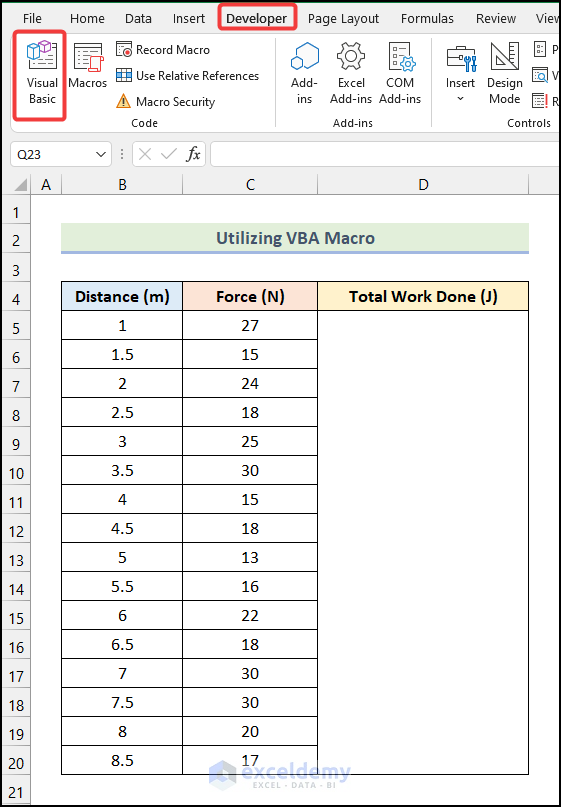
- The Microsoft Visual Basic window will open on your worksheet.
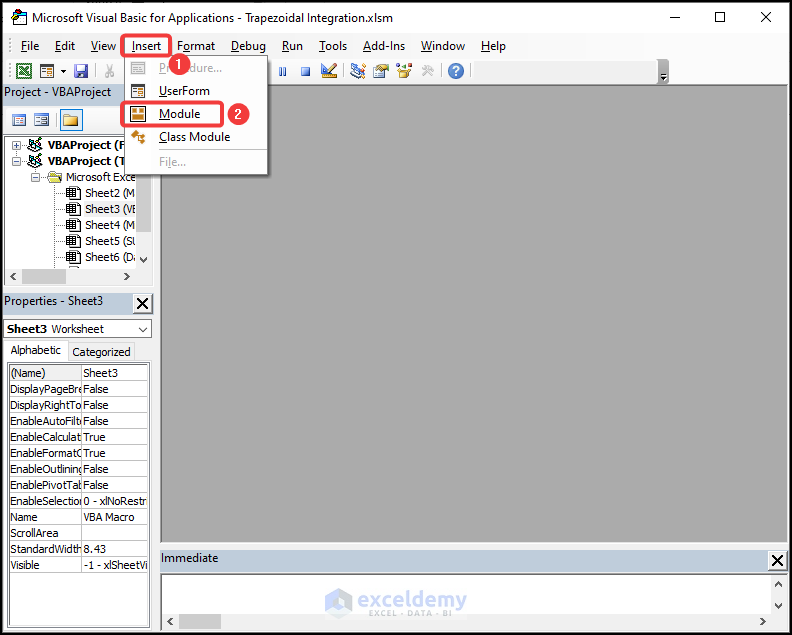
- Go to the Insert tab.
- Choose the Module option from the drop-down.
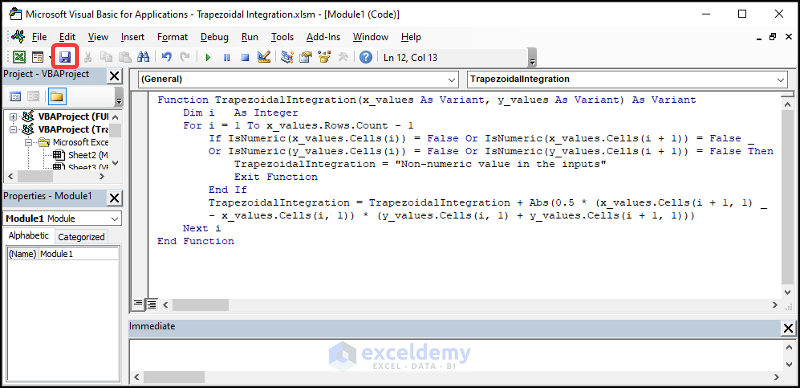
- Insert the following code in the newly created Module.
Function TrapezoidalIntegration(x_values As Variant, y_values As Variant) As Variant
Dim i As Integer
For i = 1 To x_values.Rows.Count - 1
If IsNumeric(x_values.Cells(i)) = False Or IsNumeric(x_values.Cells(i + 1)) = False _
Or IsNumeric(y_values.Cells(i)) = False Or IsNumeric(y_values.Cells(i + 1)) = False Then
TrapezoidalIntegration = "Non-numeric value in the inputs"
Exit Function
End If
TrapezoidalIntegration = TrapezoidalIntegration + Abs(0.5 * (x_values.Cells(i + 1, 1) _
- x_values.Cells(i, 1)) * (y_values.Cells(i, 1) + y_values.Cells(i + 1, 1)))
Next i
End Function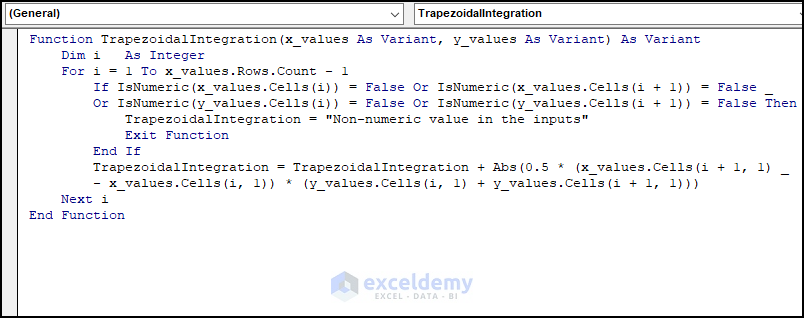
Code Breakdown
- We declared a function named TrapezoidalIntegration and its data type ss Variant.
- Inside the parentheses, we declared 2 variables x_Values and y_Values, and both of their data types are as Variant.
- We introduced another variable i as Integer.
- We initiated a For Next loop from i = 1 to the 1 less of the number of rows that have the x_values.
- We used an IF statement and in the IF statement, we used the IsNumeric function to check whether there are any non-numeric values or not.
- If there are any non-numeric values in the inputs, the function will display Non-numeric value in the inputs and it will terminate the function.
- We used the mathematical formula to calculate the Trapezoidal Integration.
- We closed the For Next loop.
- Click on the Save option.
- Press the keyboard shortcut Alt + F11 to go to your worksheet.
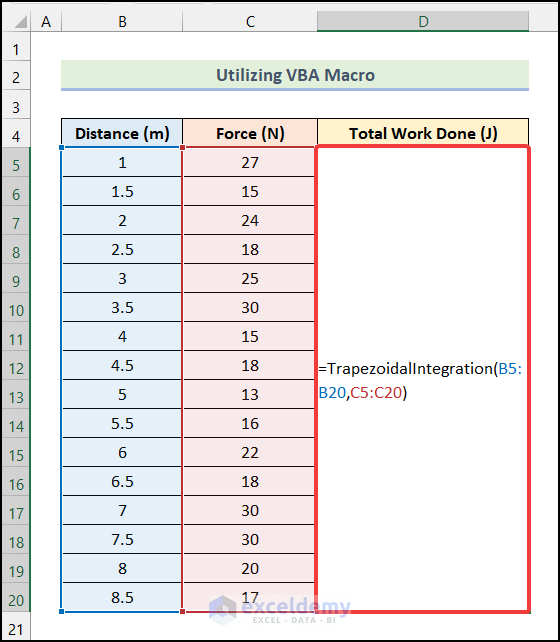
- Insert the following formula in cell D5.
=TrapezoidalIntegration(B5:B20,C5:C20)- Hit Enter.
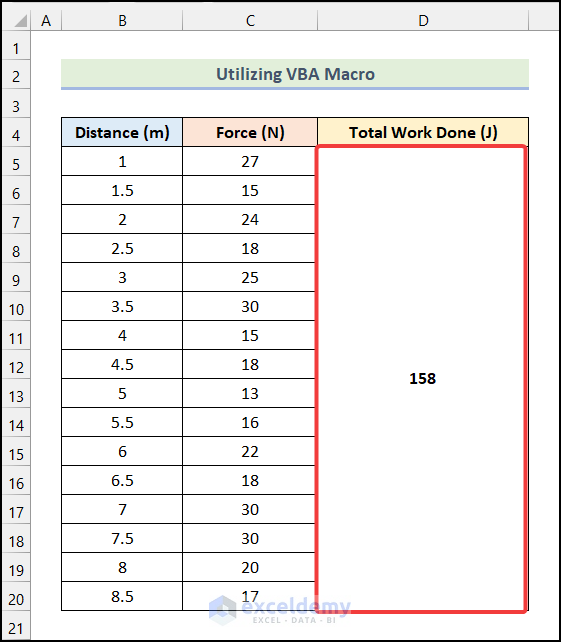
- You will have the Total Work Done (J) as shown in the image below.
Integration by Applying the Midpoint Rule in Excel
Let’s say we have a function f(x) =(1+x^3), and we need to integrate it within the limits of 1 to 5.
∫51 (1+x^3) dx
If we calculate the integral manually, we get:
[x+(x^4/4)]51 =(5+(5^4/4)) – (1+(1^4/4)) = 160
This is the Final Integral Value calculated manually.
Step 1 – Calculate the dx Value
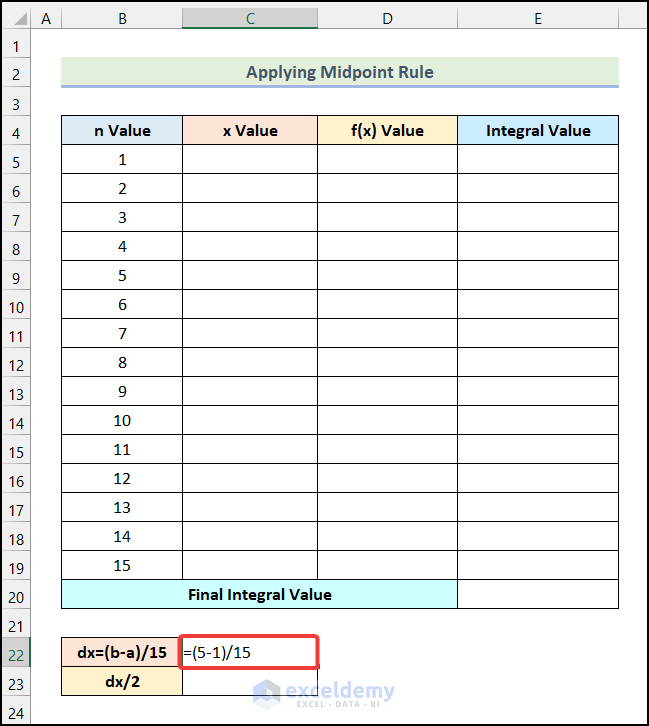
- Enter the following formula in cell C22.
=(5-1)/15Here, 5 and 1 represent the b and a values, respectively, which are the upper bound and the lower bound of the integral. And 15 is the number of steps (n Value).
- Press Enter.
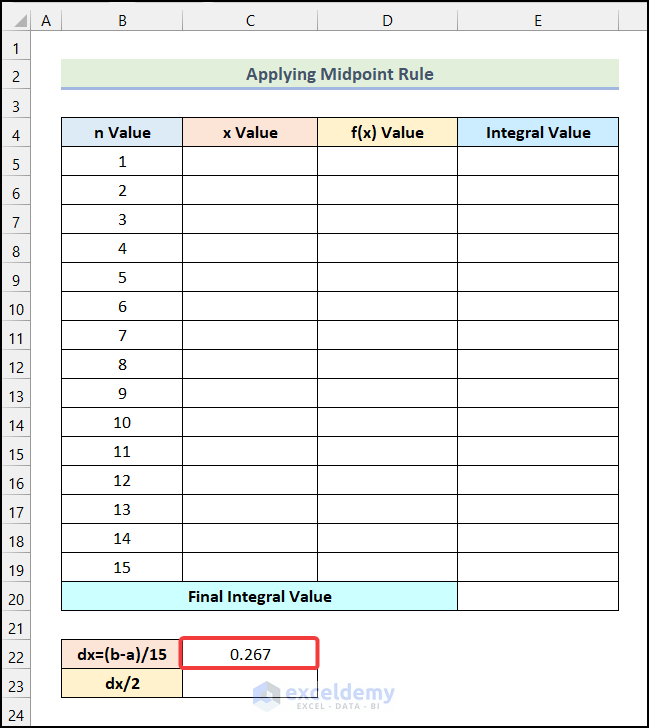
- You will get the following output in cell C22.
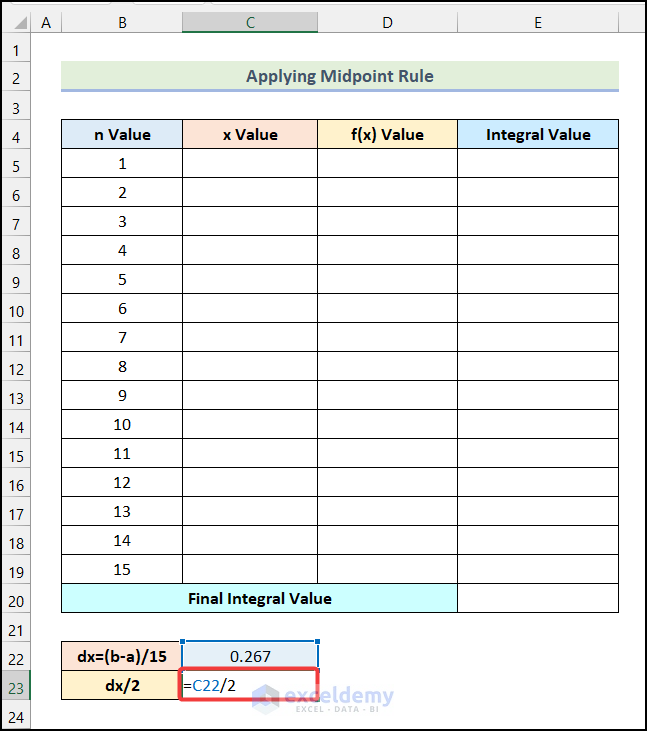
- Enter the formula given below in cell C23.
=C22/2Here, cell C22 represents the value of dx.
- Press Enter.
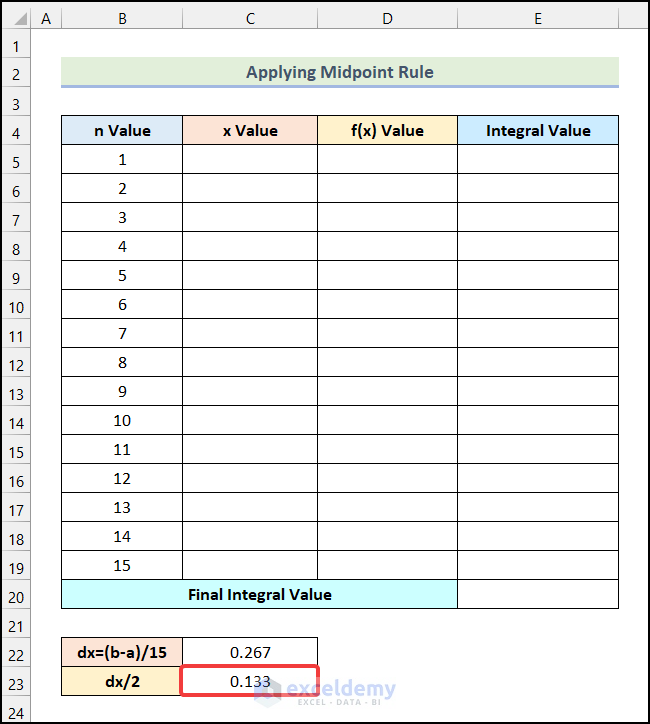
- You will get the following output in cell C23.
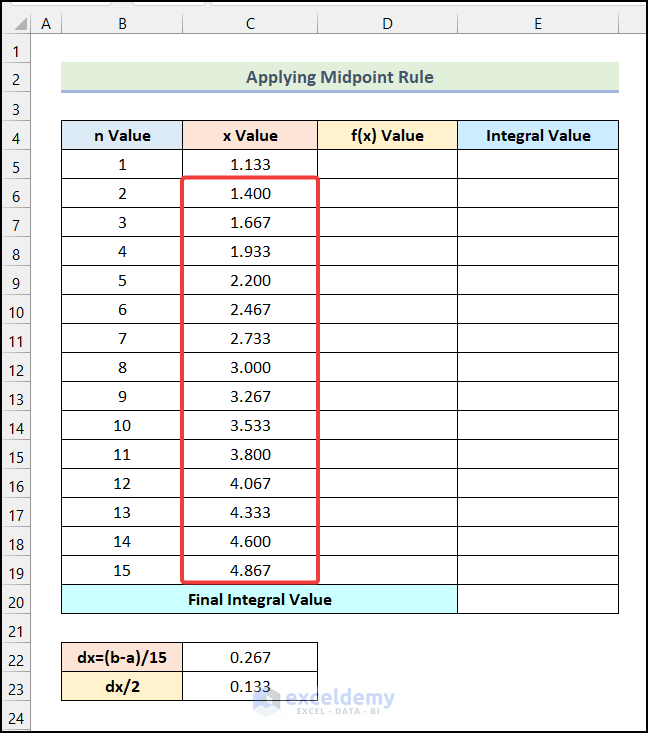
Step 2 – Find the X Value
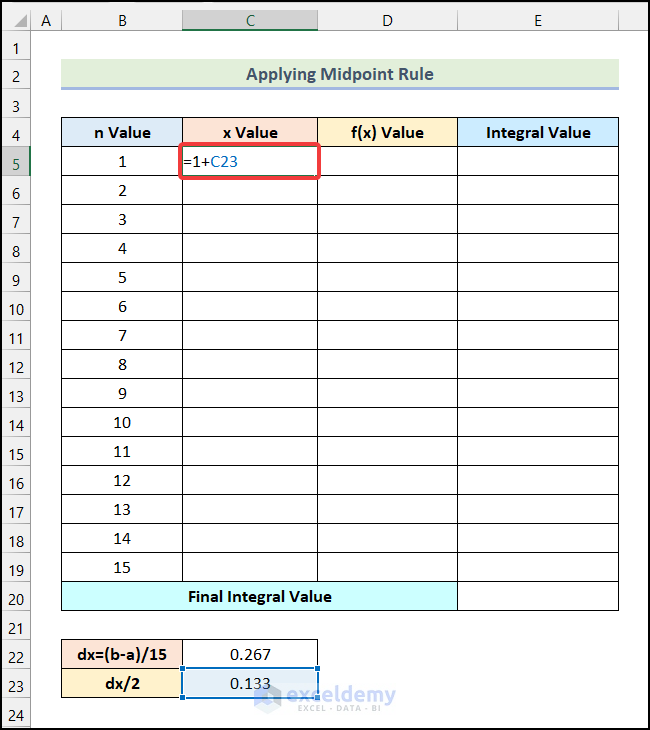
- Insert the following formula in cell C5.
=1+C23Here, cell C23 indicates the value of dx/2.
- Hit Enter.
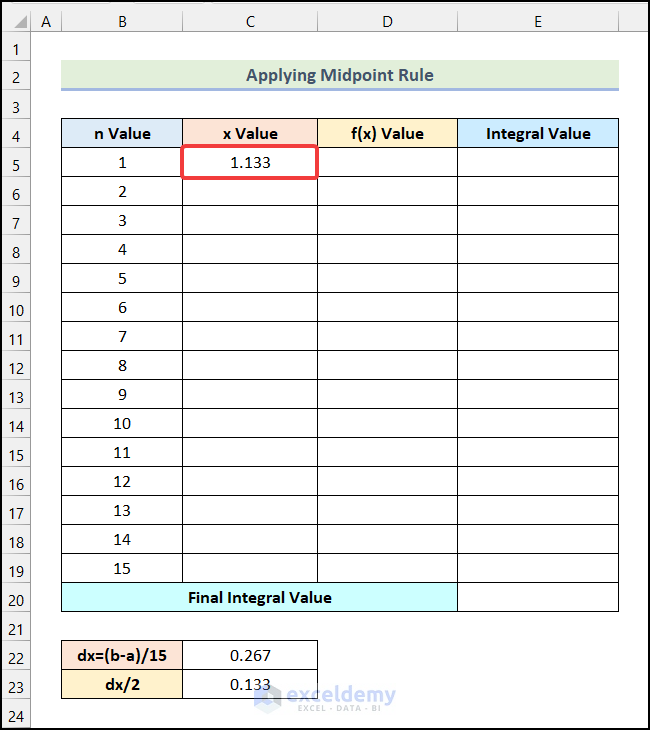
- You will get the x Value for the 1st step as shown in the following image.
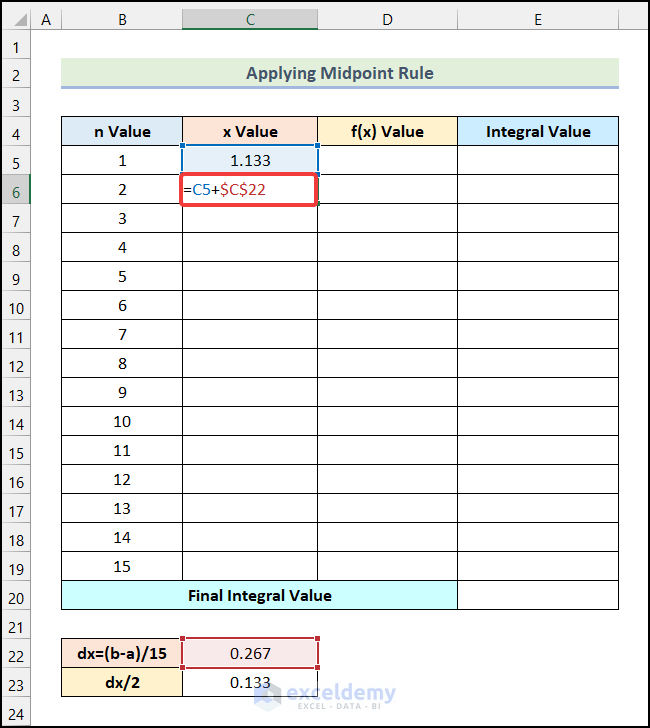
- Use the formula given below in cell C6.
=C5+$C$22- Press Enter.
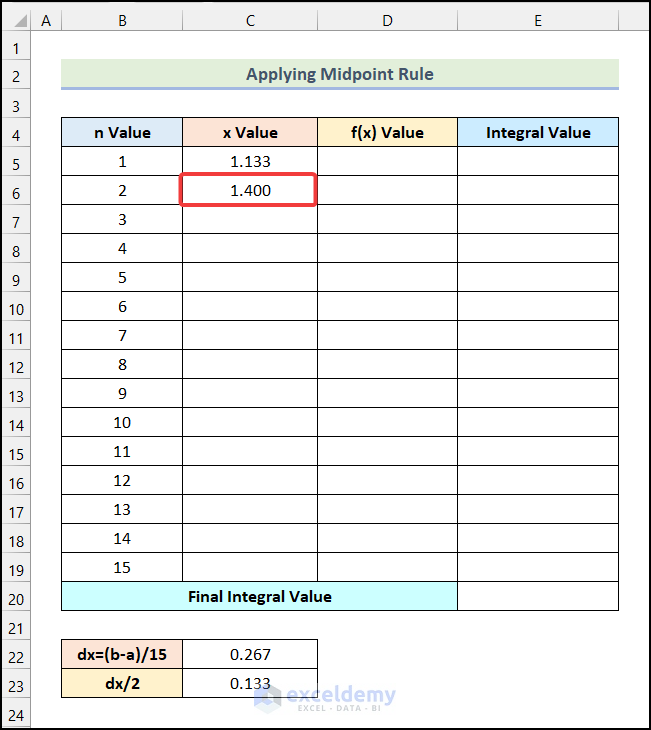
- You will get the x Value for the 2nd step.
- Drag the Fill Handle down to cell C19 to obtain the x Values for the remaining steps.
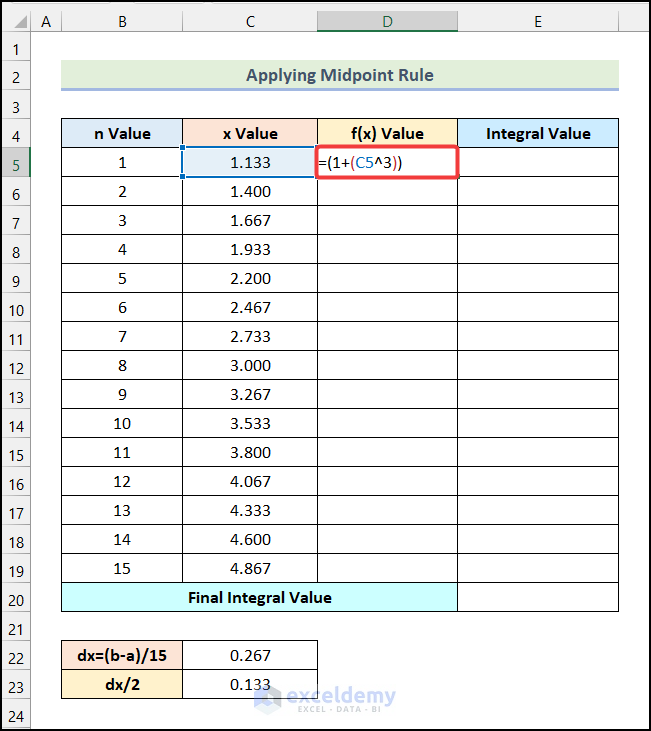
Step 3 – Compute the f(x) Value
- Enter the following formula in cell D5.
=(1+(C5^3))Here, cell C5 refers to the x Value of the 1st step.
- Press Enter.
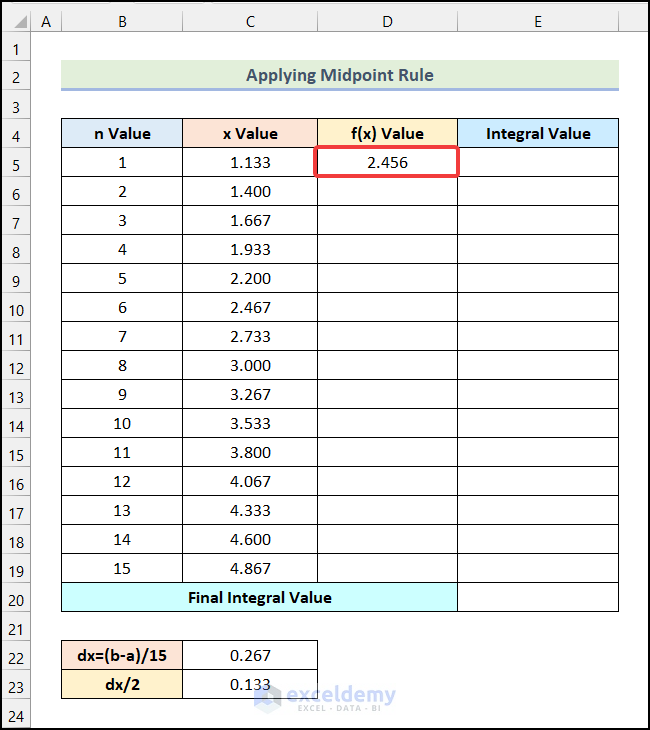
- You will get the f(x) Value for the 1st step as shown in the image below.
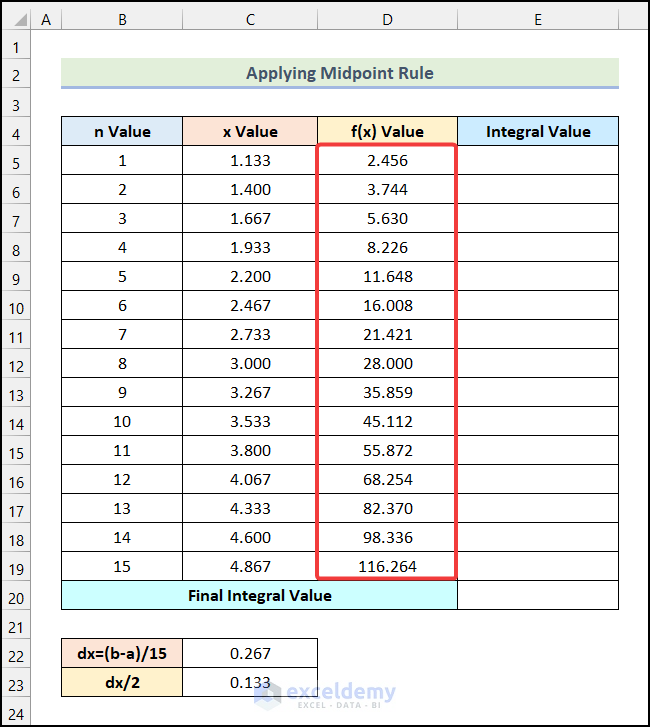
- Drag the Fill Handle to get the rest of the f(x) Values.
Step 4 – Calculate the Final Integral Value
- Apply the formula below in cell E5.
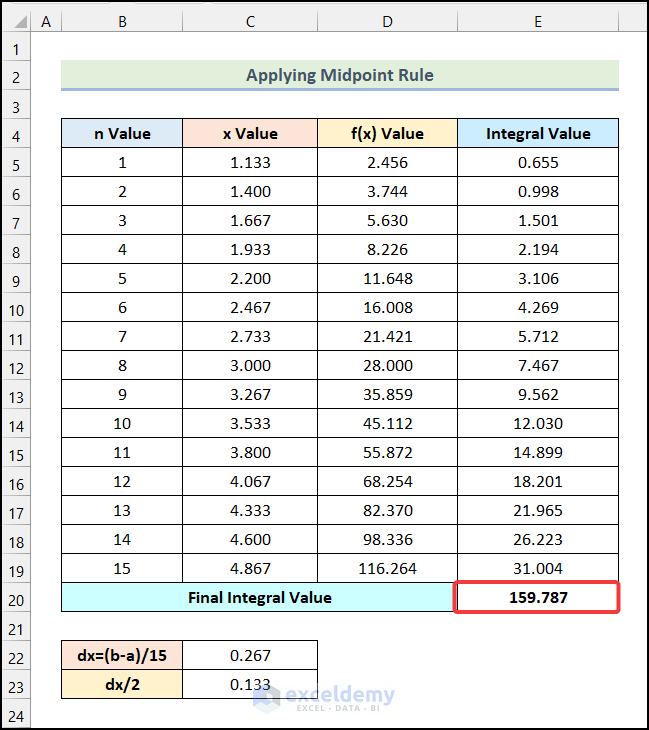
=D5*$C$22Cell D5 indicates the f(x) Value for the 1st step.
- Press Enter.
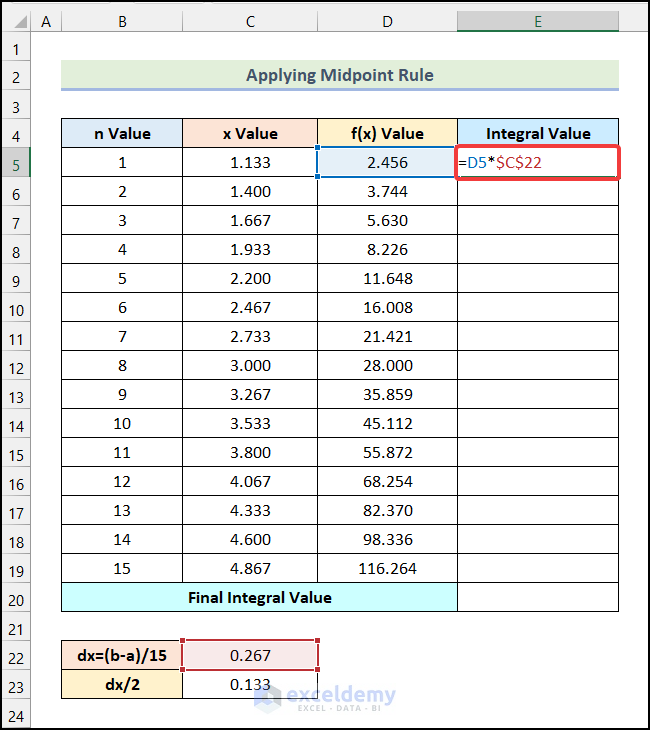
- You will have the Integral Value for the 1st step.
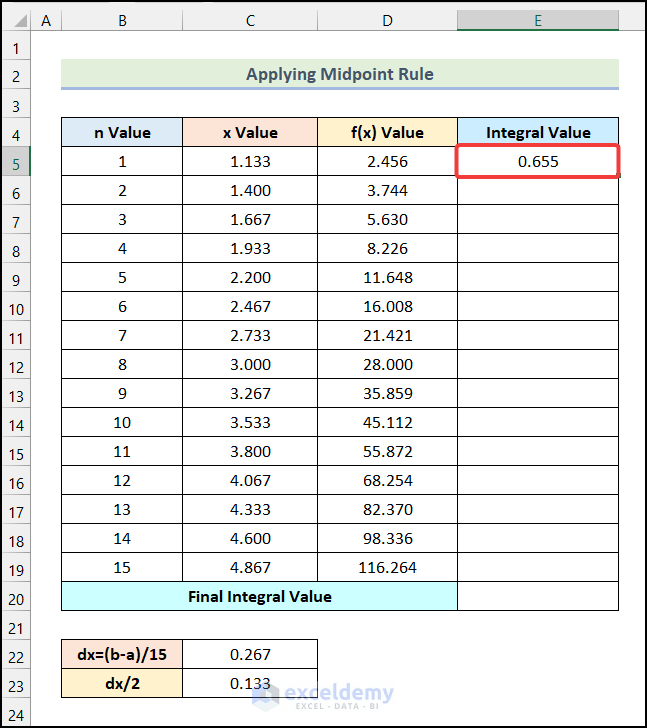
- Drag the Fill Handle to get the remaining f(x) Values.
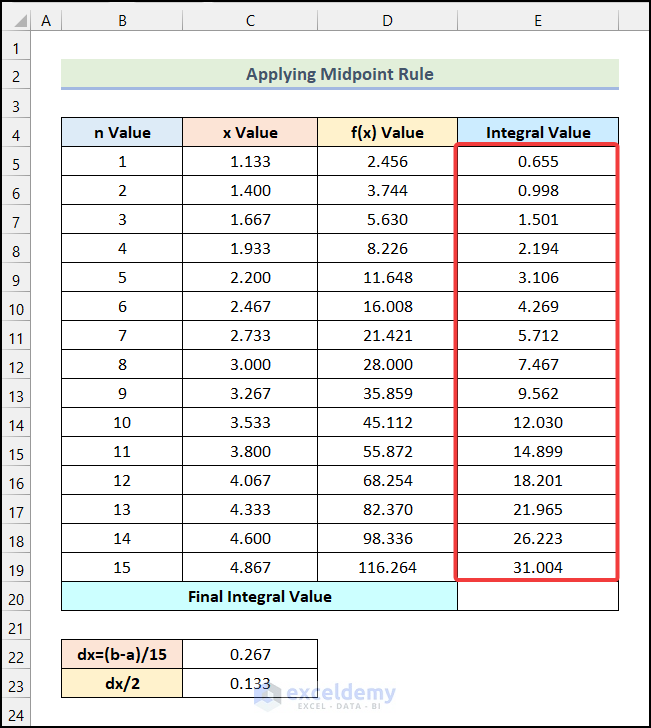
- Enter the following formula in cell E20.
=SUM(E5:E19)Here, the range E5:E19 refers to the cells of the Integral Value column.
- Hit Enter.
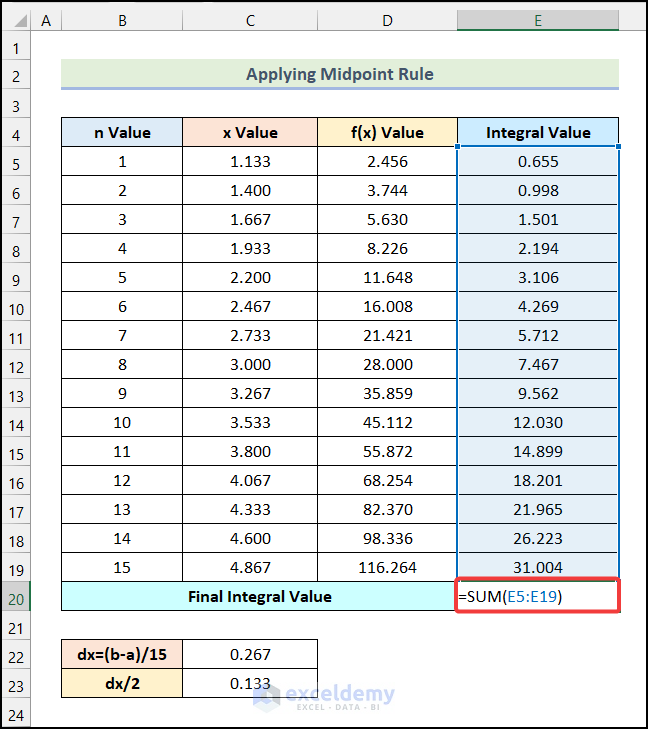
- You will get the Final Integral Value in cell E20 as demonstrated in the following picture.
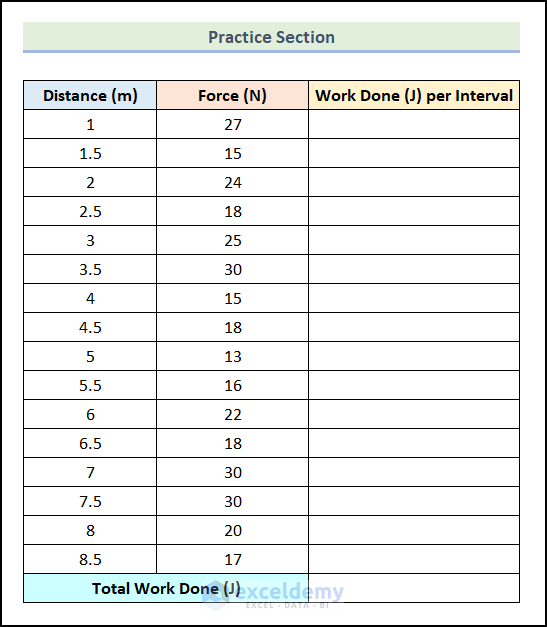
Practice Section
In the Excel Workbook, we have provided a Practice Section on the right side of the worksheet.
Download the Practice Workbook
<< Go Back to | Calculus in Excel | Excel for Math | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!

