Outliers may need to be identified in order to do statistical computations on data from a data set. You can discover outliers from huge datasets using Microsoft Excel in numerous ways. In this post, we’ll show you how to calculate outliers in Microsoft Excel using five distinct ways.
Outliers are data values that are significantly different from the rest of the data values in the dataset. Outliers, in other words, are extraordinary values. They are either exceptionally high or excessively low in comparison to other values in a data set. Finding outliers is vital in statistical calculations since they have an impact on the findings of our data analysis.
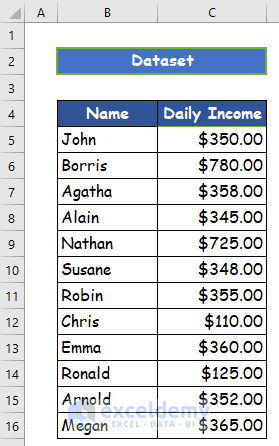
For example, you have a data set showing the daily income of twelve people. Now, you need to calculate the outliers using Microsoft Excel. Here, I will show you five easy approaches to do so.
1. Using Sort & Filter to Calculate Outliers in Excel
You may calculate outliers from a small data set by utilizing the Sort & Filter command in Excel. If you wish to calculate outliers using the sort and filter function, you can do it by following the steps below.
Step 1:
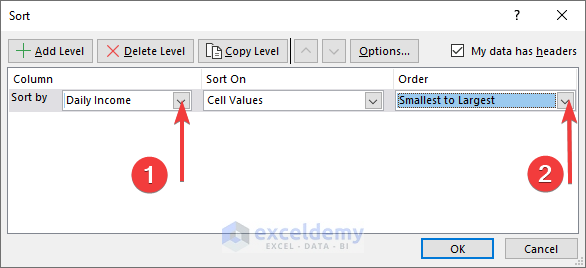
- Firstly, select the column header in your dataset of excel that you want to sort. For example, in the given data set, in the file column header named Daily Income (Cell C40 is chosen).
Step 2:
- Then, press the Home tab on the ribbon and go to the Editing group.
Step 3:
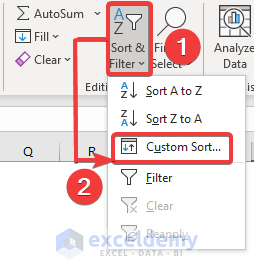
- After that, in the Editing group click on the Sort & Filter command and click on the Custom Sort.
Step 4:
- Then, a new dialog box named Sort will open. In the popped-up dialog box, select Daily Income in the Sort by drop-down and Smallest to Largest in the Order drop-down. After that, click OK.
Step 5:
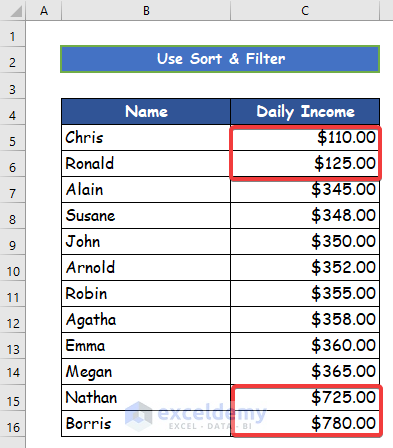
- Finally, the Daily Income column would be sorted in the manner stated, with the lowest values at the top and the greatest values at the bottom. After running the procedure, look for any irregularities in the data range to determine outliers.
For example, the first two values in the column are significantly lower and the last two values in the column are substantially higher than the rest of the values in the data set, as shown in the above result.
Read More: How to Find Outliers in Regression Analysis in Excel
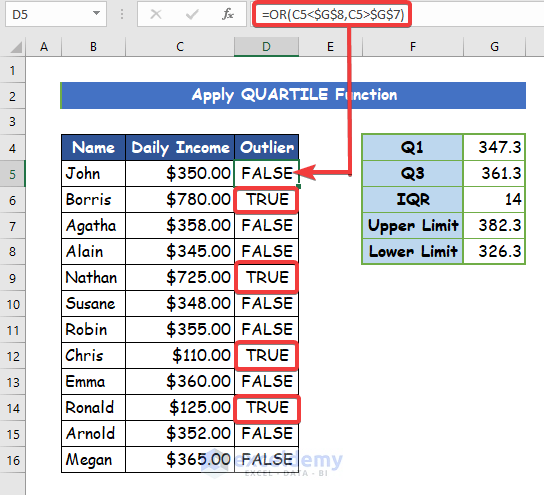
2. Applying QUARTILE Function to Determine Outliers in Excel
The QUARTILE function approach is a more scientific way to calculate outliers in Excel. You can use this function to divide your data sets into four equal portions. The following values will be returned by the QUARTILE function:
- The minimum value.
- The 1st quartile (Q1- lowest 25% of a given dataset).
- The 2nd quartile (Q2-next lowest 25% of the dataset).
- The 3rd quartile (Q3- second highest 25% of the dataset).
- The maximum value.
The syntax of the QUARTILE function in Excel is:
=QUARTILE(array,quart)
The syntax contains the following arguments:
- array: the cell range of a given data set for which you will calculate the quartile value.
- quart: This specifies which value should be returned.
For calculating the outliers for the above dataset using the QUARTILE function, follow the steps below.
Step 1:
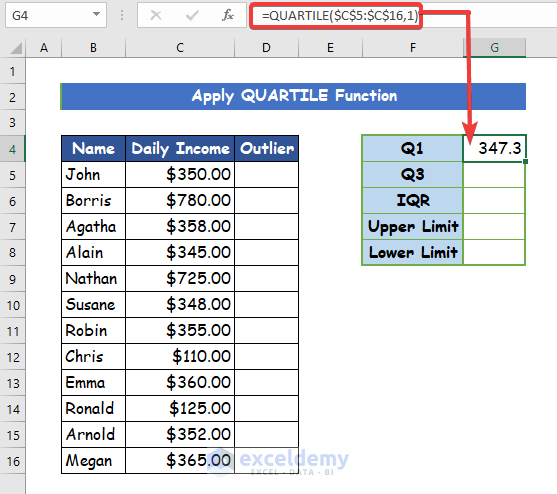
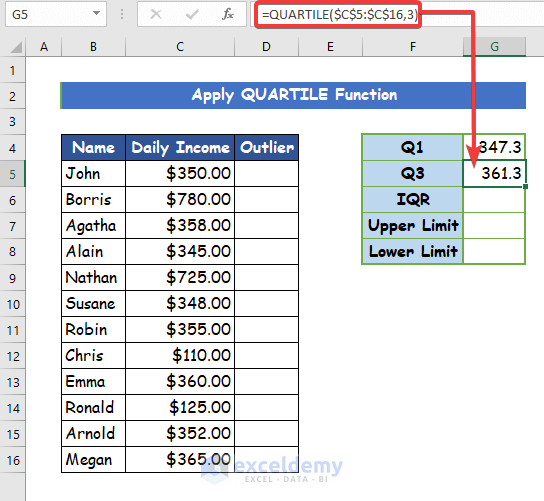
- Firstly, type the following formula for determining the 1st quartile (Q1) is given below.
=QUARTILE($C$5:$C$16,1)Step 2:
- Here again, the formula to calculate the 3rd quartile (Q3) is given below.
=QUARTILE($C$5:$C$16,3)Step 3:
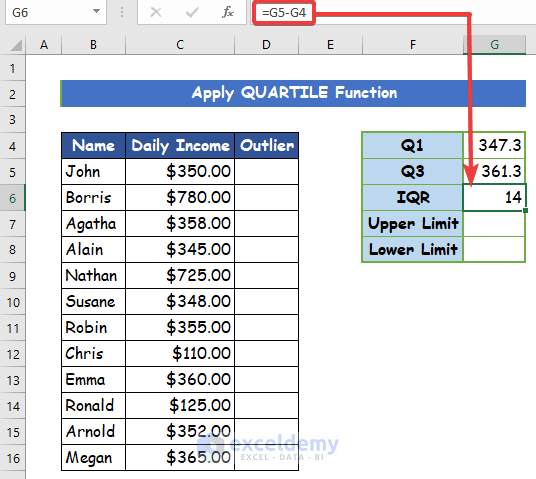
- Thirdly, you have to determine the IQR, which is the Inter-Quartile Range (it represents 50% of the given data from a range of data set that fall into the first and third quartiles) by subtracting Q1(in cell G4) from Q3(in cell G5). Type the following formula to calculate the subtraction.
=G5-G4
Step 4:
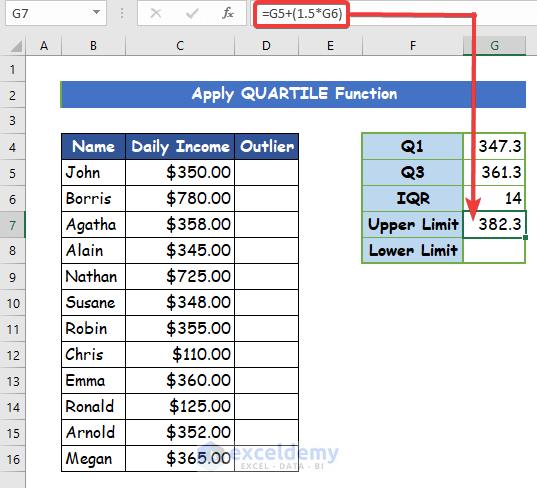
- After finding IQR, next you have to determine the upper and lower Because the upper and lower limit would contain most of the data within the data set. Write down the following formula to calculate the upper limit.
=G5+(1.5*G6)
Step 5:
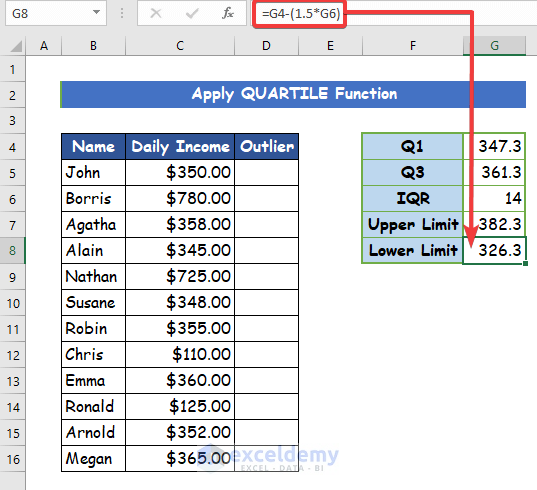
- Then, to calculate the lower limit, write down the following formula.
=G4-(1.5*G6)Step 6:
- Finally, after finishing the previous step, you can determine outliers for each data value. In the excel worksheet, type the following formula with the OR function in cell D5.
=OR(C5<$G$8,C5>$G$7)- This formula will help to identify the data which do not fall within the above-mentioned range limit. After processing the formula will show a TRUE Statement if the specific data is an outlier and FALSE if it is not. Double-click on the AutoFill tool in cell C5 to copy the formula to the rest of the cells in column C. Thus, you can observe a True value next to all the outliers in your dataset.
3. Combining AVERAGE and STDEV.P Functions to Calculate Outliers from Mean and Standard Deviation
A standard deviation (or σ) is a metric for determining how distributed the data are regarding the mean value of the whole data set. Data is grouped around the mean when the standard deviation is low, while data is more spread out when the standard deviation is high. To calculate outliers using the Mean and Standard Deviation you can follow the following steps.
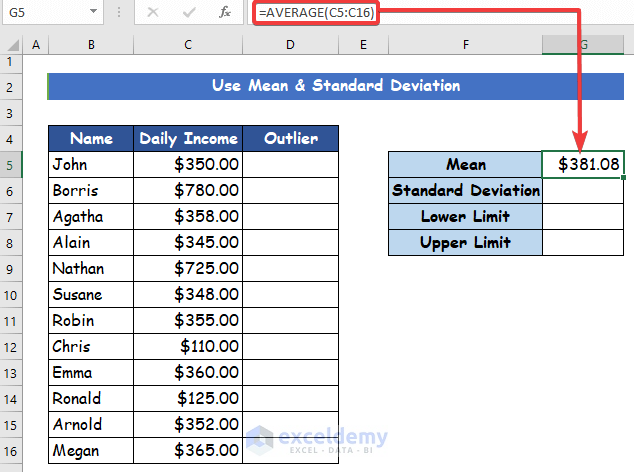
Step 1:
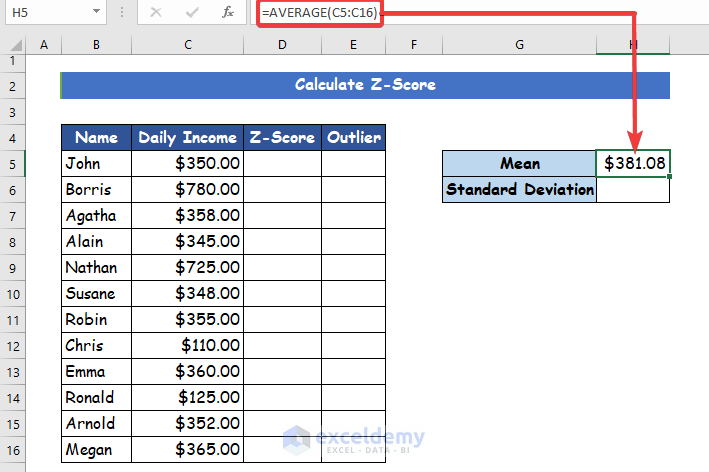
- Firstly, use the same dataset shown at the start of this article and then calculate the mean and standard deviation. To calculate the mean, type the following formula with the AVERAGE function in cell G5.
=AVERAGE(C5:C16)Step 2:
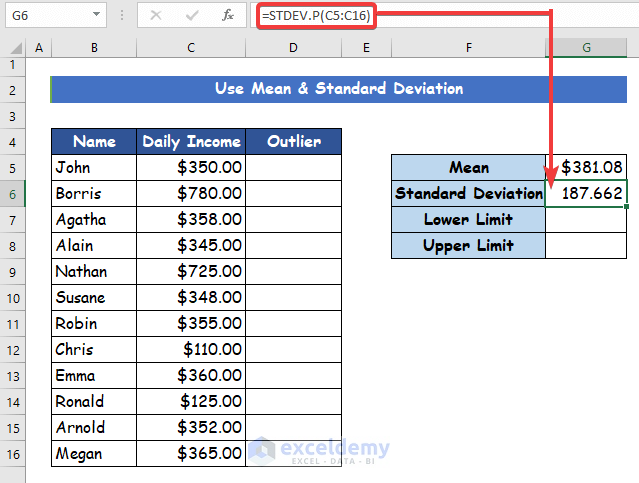
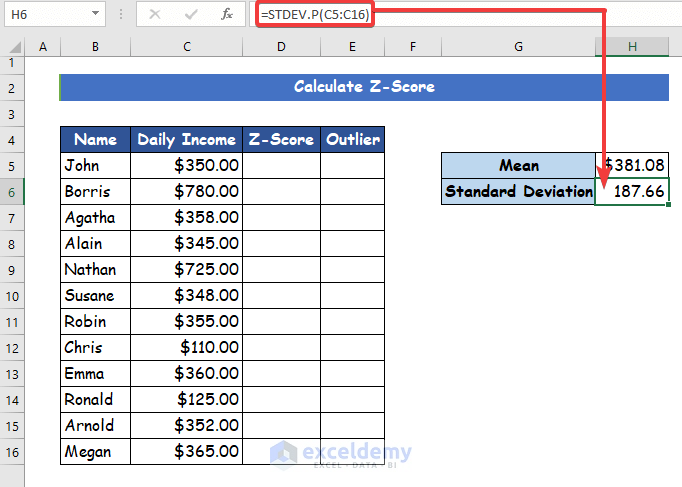
- To calculate the standard deviation, insert the following formula with the STDEV.P function in cell G6.
=STDEV.P(C5:C16)Step 3:
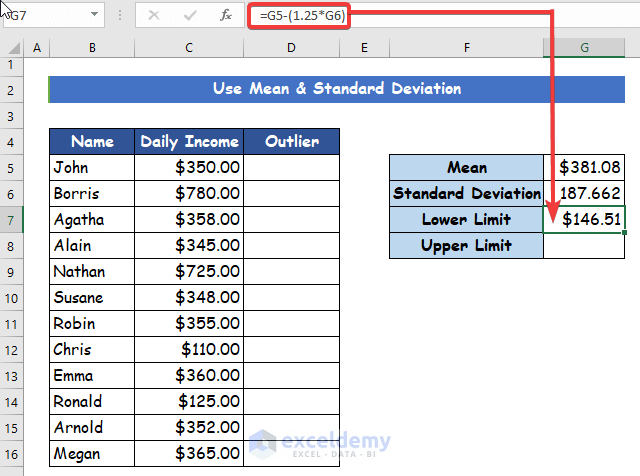
- Next, you will calculate the upper limit for further advancement in the process. In cell G7, calculate the lower limit by using the following formula.
=G5-(1.25*G6)Step 4:
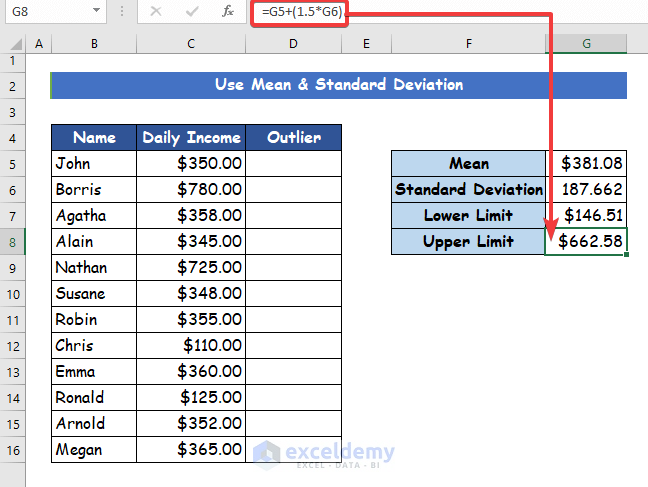
- And in cell G8 calculate the upper limit from the following formula
=G5+(1.5*G6)Step 5:
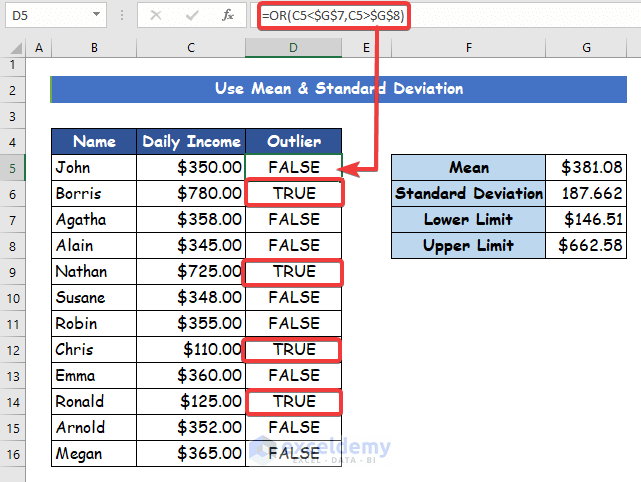
- After that, to calculate if any outliers exist or not, type the following formula in cell D5.
=OR(C5<$G$7,C5>$G$8)- Thus, the formula will return a TRUE value if the specific data in the desired cell is an outlier and FALSE.
- Double-click on the AutoFill tool in cell D5 to copy the formula to the rest of the cells in column D. Thus, you can find out all the remaining outliers in your dataset.
Read More: How to Find Outliers with Standard Deviation in Excel
4. Inserting Z-Score to Calculate Outliers in Excel
The Z-score is one of the most often used metrics for identifying outliers. This method shows how far a specific data is from the mean of a dataset with respect to its standard deviation. To calculate outliers using Z-score in Excel you can see the steps described below.
Step 1:
- Firstly, take the desired data set.
Step 2:
- Secondly, in cell H5, type the following formula for calculating the mean for the given data.
=AVERAGE(C5:C16)Step 3:
- Thirdly, calculate the standard deviation of the given dataset in cell H6 by using the following formula.
=STDEV.P(C5:C16)Step 4:
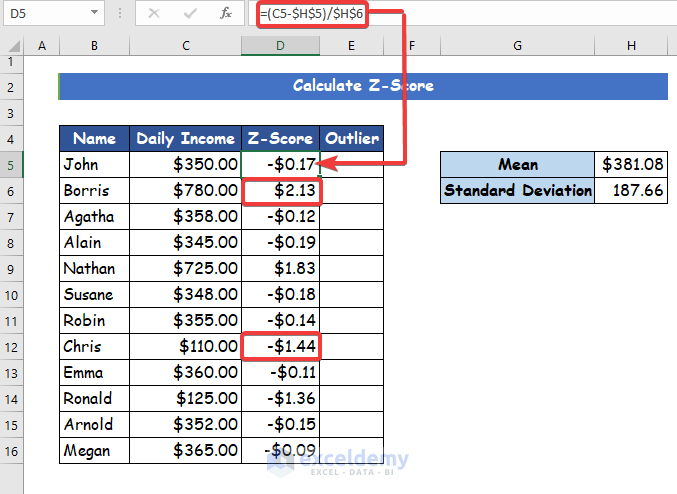
- After that, you have to determine the Z-score for each data value. To do this you use the formula given below.
=(C5-$H$5)/$H$6Step 5:
- After calculating all the Z-values, you will see that the range of Z-values is between -1.44 and 13. So, we consider values of Z-score less than -1.2 or more than +1.8 for the outlier limits.
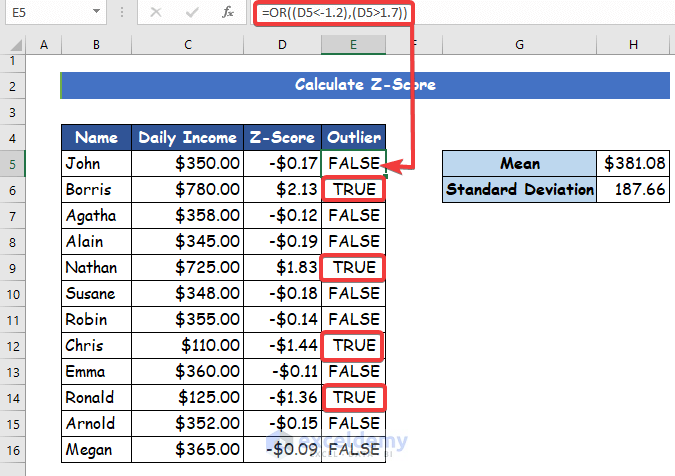
- Then, type the following formula into cell E5.
=OR((D5<-1.2),(D5>1.8))- Finally, the formula will return a TRUE value if the specific data is an outlier and will return FALSE
- Double-click on cell E5 to use the AutoFill tool fill handle to copy the formula to the rest of the cells in column E. Thus, you can find all the remaining outliers in your dataset.
Read More: How to Find Outliers Using Z Score in Excel
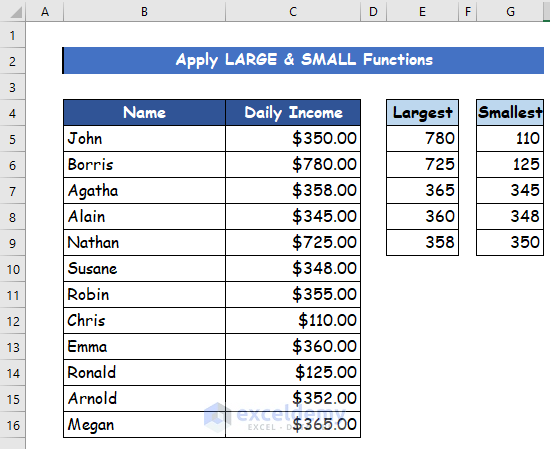
5. Merging LARGE and SMALL Functions to Find Outliers in Excel
The LARGE function and the SMALL function in Excel have opposite operations. We will use it to find the greatest and smallest data or values in a data set, respectively. This function will pull all the data within a data set, finding the smallest and largest numbers. They are able to find the second smallest or largest, the third-largest or smallest, and so on.
Step 1:
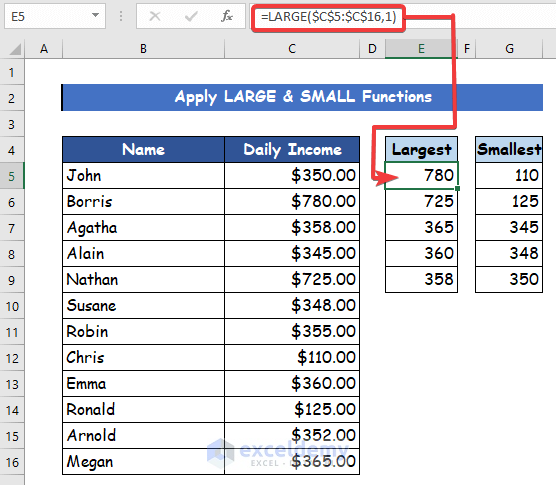
- Firstly, use the following formula in cell E5 with the LARGE function.
=LARGE($C$5:$C$16,1)-
- Thus, from 12 values, you can see the 1st largest value which is 780.
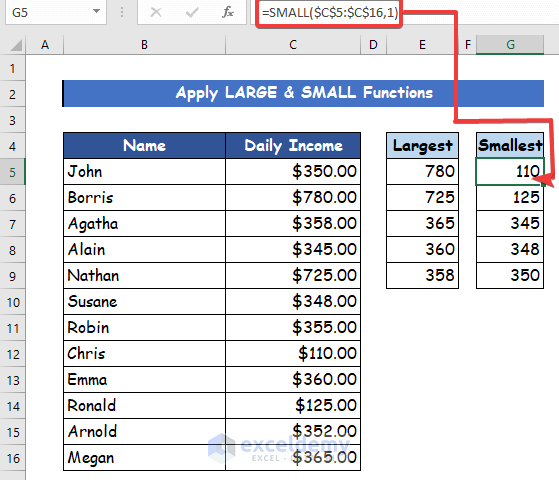
Step 2:
- After that, in cell G5, write down the following formula to find the smallest value.
=SMALL($C$5:$C$16,1)- Finally, from 12 values, you can see the 1st smallest value 110.
- Once you have found out all the required values, then you can easily point out any outliers in the dataset.
Download Practice Workbook
You can download the free Excel workbook from here and practice on your own.
Conclusion
That’s the end of this article. I hope you find this article helpful. After reading this article, you will be able to calculate outliers in Excel using any of the methods. Please share any further queries or recommendations with us in the comments section below.