How to Find Outliers Using Z Score in Excel (with Quick Steps)

In statistical probability calculations, the z score is of primary importance. Data distributions and outliers in a dataset can be determined with this term. It is possible to determine them manually from a dataset. If you have a larger dataset, there are several tools at your disposal. Excel is one of them. If you are looking for some special tricks to find outliers using z score in Excel, you’ve come to the right place. This article will discuss every step of the method to find outliers using the z score. Let’s follow the complete guide to learn all of this.

What Is Z Score?

In statistics, the z score represents the standard deviation from the population for a particular data point. This measure tells us how far a specific value is from the mean of a set in relation to its standard deviation. ( Standard deviation is the RMS value of all the different points and mean). The mathematical formula for the z score is

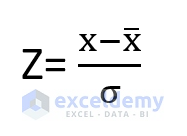
Where,

Z= z score

X=observed value

x̅= mean value

σ = standard deviation

What Is Outlier?

Outliers are values that are significantly different from other values in a dataset. Another way of saying this is that an outlier is a value that is much higher or lower than the mean and median of the dataset. In an Excel graph, you can consider the data points which remain far away from the other data points as outliers. For instance, consider a scenario where you have total points scored by 5 different players in the NBA season. The scored points are 1600, 1400, 300, and 1500. Now, if you plot a graph in Excel, you will see that point 300 lies far away from the others. So, in this 3000 is the outlier.

An outlier is considered to be a z score value within the range of 3 to -3 because these values are quite distant from the value of the mean.

How to Find Outliers Using Z Score in Excel: Step-by-Step Procedure

In the following section, we will use one effective and tricky method to find outliers using the z score in Excel. We are going to determine the z score of the sample by calculating the mean and standard deviations of all numbers. And then we will find outliers of each observation. This section provides extensive details on this method. You should learn and apply all of these to improve your thinking capability and Excel knowledge. We use the Microsoft Office 365 version here, but you can utilize any other version according to your preference.

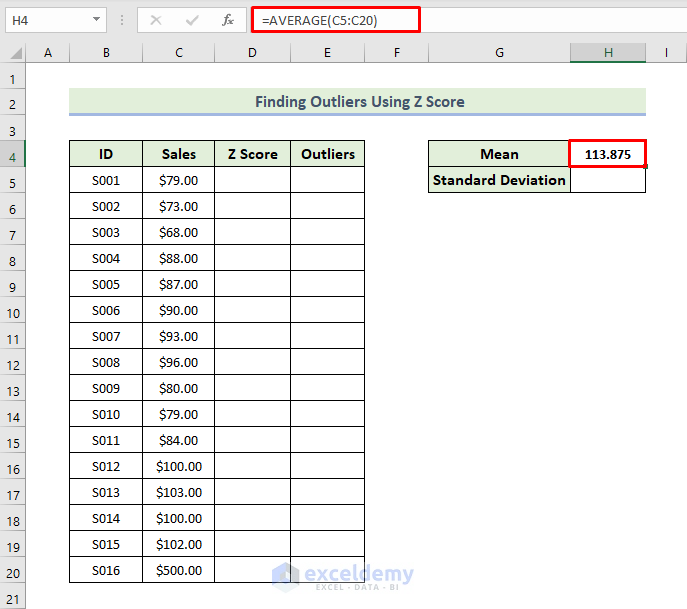
Step 1: Calculate Mean of Dataset

In the beginning, we are going to find the mean of the dataset. This will be helpful for determining the standard deviation and z score. Her, we use the AVERAGE function to determine the mean of the observation. This function takes in a series of arguments or a range of values and returns their mean. Let’s walk through the steps to calculate the mean of the dataset.

First of all, select the range of the cells and type the following formula in cell H4.

=AVERAGE(C5:C20)

Then, press Enter.
As a consequence, you will have the mean value of all the data.

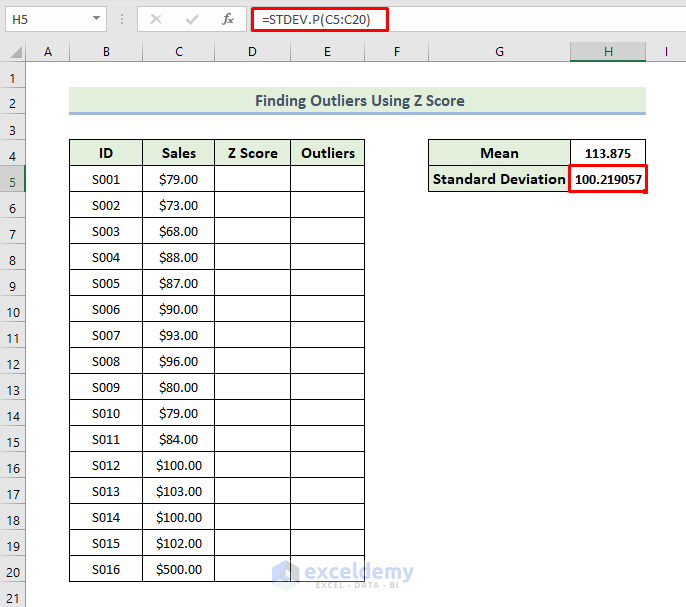
Step 2: Estimate Standard Deviation

Now, we are going to estimate the standard deviation. We will use the STDEV.P function to determine the standard deviations for the dataset. This function will return the standard deviation from a series of numbers or range of values it takes as arguments. Let’s walk through the steps to estimate the standard deviation.

First of all, select the range of the cells and type the following formula in cell H5.

=STDEV.P(C5:C20)

Then, press Enter.
As a consequence, you will have the standard deviation value for all the data.

Read More: How to Calculate Outliers in Excel

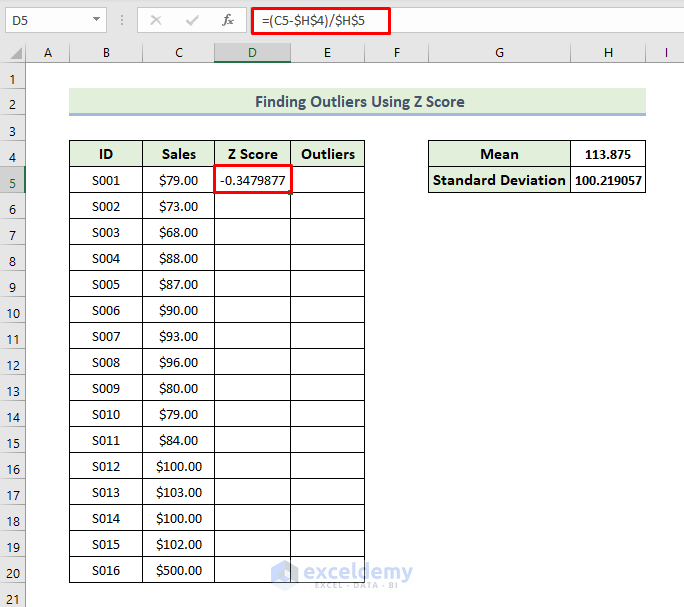
Step 3: Evaluate Z Score

Now, we are going to evaluate the z score. To determine the z score of the values, first of all, we need the difference of the value from the mean and then divide it by the standard deviation according to the formula. Let’s walk through the steps to estimate the z score.

First of all, to evaluate the z score, you have to type the following formula in cell D5.

=(C5-$H$4)/$H$5

Then, press Enter.
As a result, you will have the z score for the first value in the dataset.

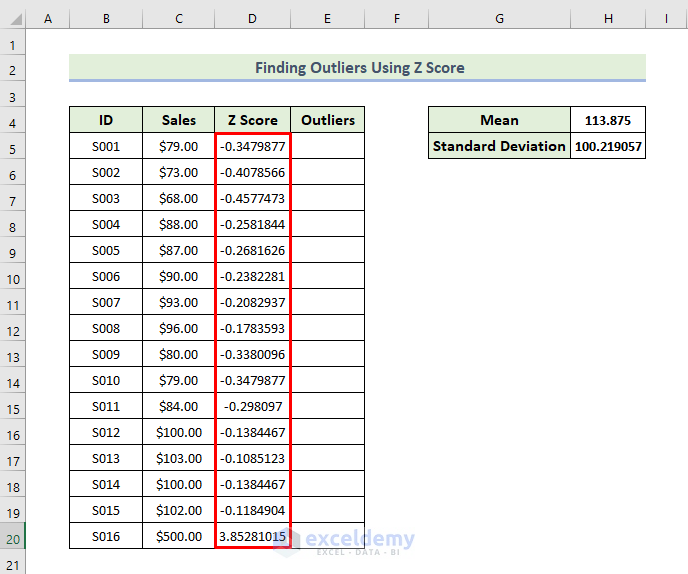
Next, drag the Fill Handle icon to fill out the rest of the cells in the column with the formula.
As a consequence, you will get the z score for all the entries of the dataset.

In our dataset, the mean value is 113.875 and the standard deviation is 100.21. Now, if we consider the specific value of $79, the z score for this value is -0.347 which means $79 is 0.347 standard deviations below the mean or average value.
In another case, when the value is $500, we get the z score is 3.85. That means $500 is 3.85 standard deviations above the mean value.

Step 4: Find Outliers from Dataset

Now we are going to find out outliers in our dataset. An outlier is considered to be a z score value within the range of 3 to -3, as mentioned above. Let’s walk through the steps to find out the outliers in the dataset. Here, we will use the OR function to find out whether the values in the dataset contain outliers or not. If any of the values within the range satisfy the condition then the result will be TRUE.

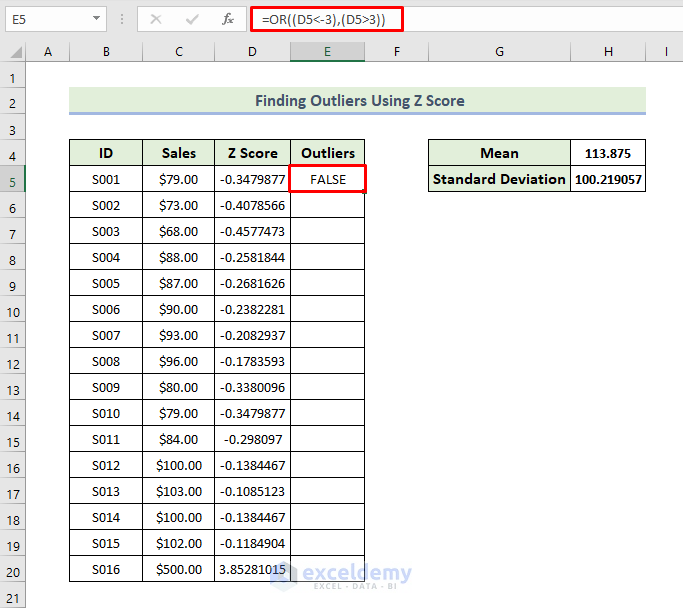
First of all, to find outliers, you have to type the following formula in cell E5.

=OR((D5<-3),(D5>3))

Then, press Enter.
As a result, you will find out whether the first value contains outliers or not in the dataset.

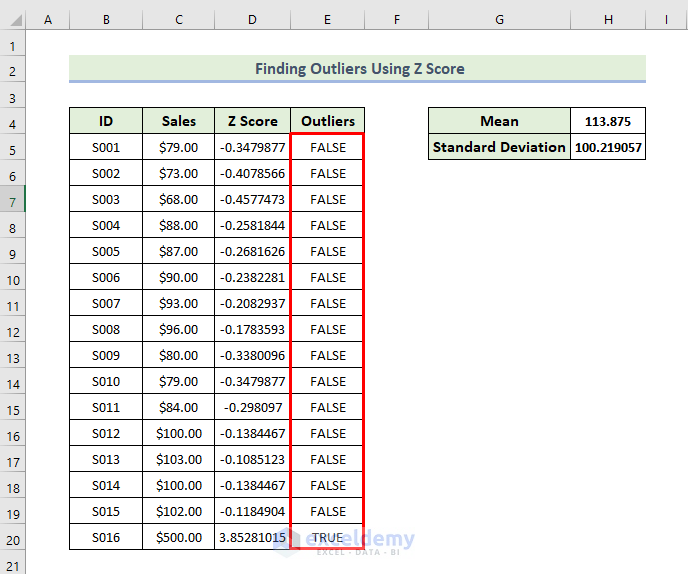
Next, drag the Fill Handle icon to fill out the rest of the cells in the column with the formula.
As a consequence, you will be able to know whether the values in the dataset contain outliers or not as shown below.

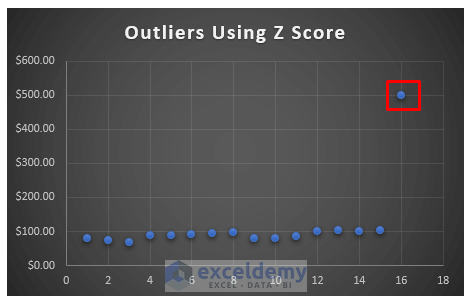
From the above dataset, we can see only one id’s z score is above the value of 3. That’s why we only get one outlier.

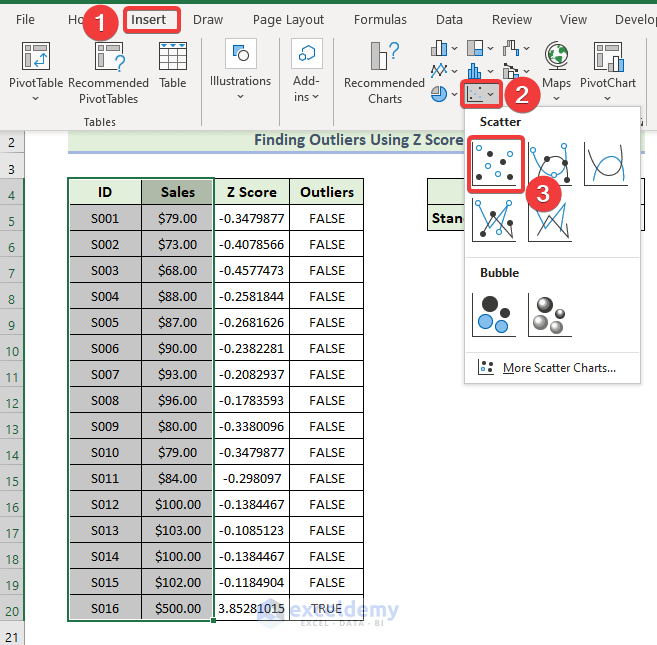
Now, we are going to show outliers using a Scatter chart. We have to follow the following process:

Firstly, select the range of the cells C5:D20.
Then, go to the Insert tab. Select Insert Scatter (X, Y) or Bubble Chart, and finally select Scatter.

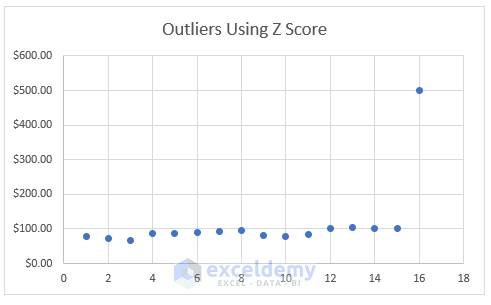
As a consequence, you will get the following chart.

To modify the chart style, select Chart Design and then, select your desired Style 9 option from the Chart Styles group.

As a consequence, you will get the following Scatter chart.

Download Practice Workbook

Download this practice workbook to exercise while you are reading this article. It contains all the datasets in different spreadsheets for a clear understanding. Try yourself while you go through the step-by-step process.

Find Outliers Using Z Score.xlsx

Conclusion

That’s the end of today’s session. I strongly believe that from now you may be able to find outliers using z score in Excel. If you have any queries or recommendations, please share them in the comments section below.

<< Go Back to Outliers in Excel | Excel for Statistics | Learn Excel

Get FREE Advanced Excel Exercises with Solutions!