The sample dataset is a graphical representation of the equation y=sinx ranging from 0 to pi. The graph has a peak at sin (pi/2) where the corresponding y value is 1. We will calculate the area of this graph.
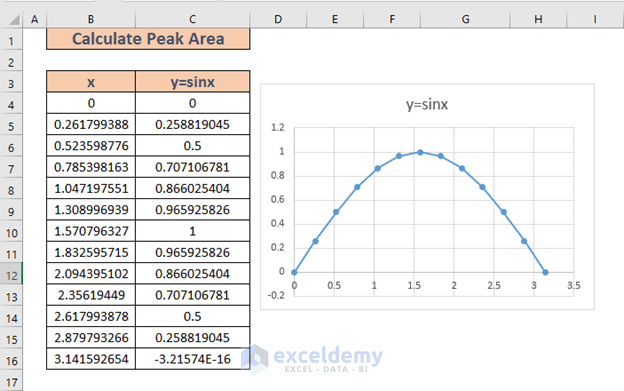
Method 1 – Use the Trapezoidal Rule to Calculate the Peak Area in Excel
In this method, we will divide the curve into some smaller trapezoids. Then, we will calculate the area for those trapezoids individually and then add those small areas to get the final area.
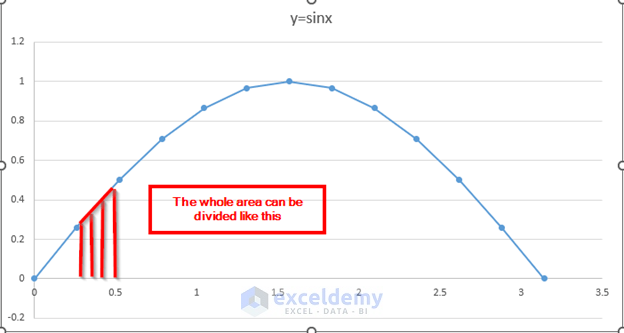
The small segments are like trapezoids. The smaller the segments are, the more they resemble a trapezoid.
Steps:
- Go to D5 and insert the following formula.
=(C5+C4)/2*(B5-B4)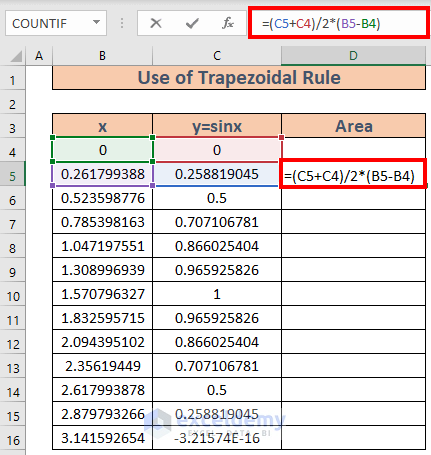
Explanation:
- C4 and C5 represent the lengths of the parallel lines here. These are along y-axis in the graph.
- (B5-B4) represents the distance between the parallel lines. They are along x-axis in the graph.
- Press Enter. Excel will calculate the area for a trapezoid.
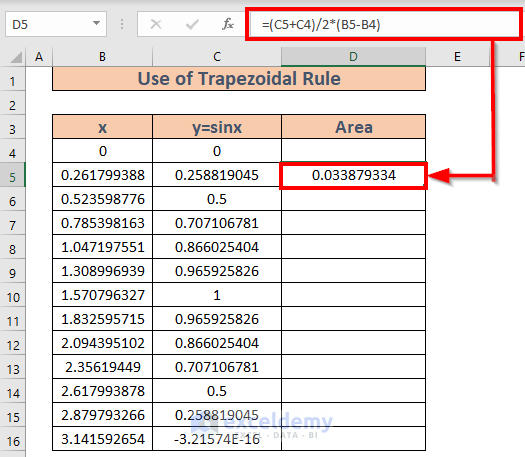
- Use the Fill Handle to AutoFill to D16.
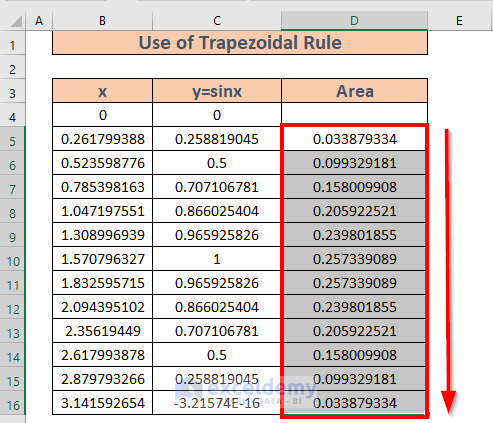
- Add the areas using the SUM function in D18:
=SUM(D5:D16)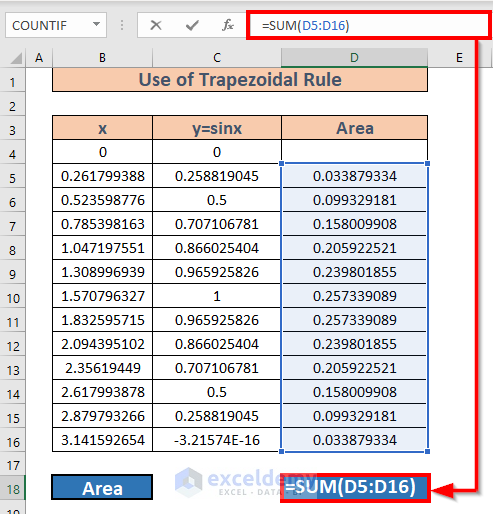
- Press Enter.
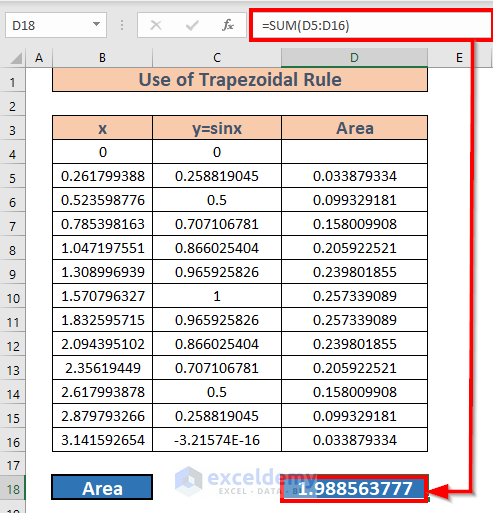
Note: The result is not exactly 2 as it should be. That’s because we assumed the segments as trapezoids, but they are not perfect trapezoids. Had the segments been smaller, they would have resembled trapezoids more and we would have got the result closer to 2.
Method 2 – Apply a Definite Integral Rule to Calculate Peak Area in Excel
Steps:
- We have to determine the integral form of sinx. The integration of sinx is –cosx. We will ignore the constant value since our final target is to determine the definite integration of sinx ranging from 0 to pi.
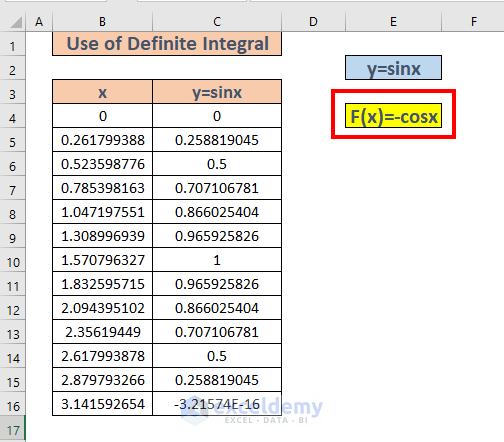
- The range is from 0 to pi. We will calculate -cos(0) and -cos(pi). The corresponding values are -1 and 1.
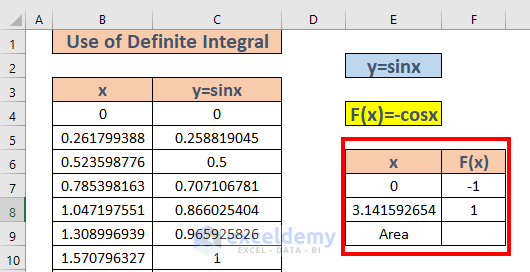
- Our upper limit is pi and the lower limit is 0. We will subtract -cos(0) from -cos(pi). Go to F9 and write down the formula
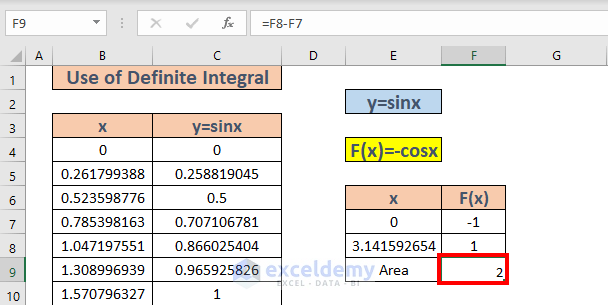
=F8-F7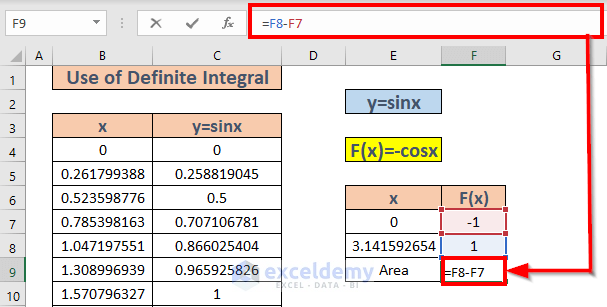
- Hit Enter.
Things to Remember
- The equation for the area of a trapezoid is A = (a+b)/2 * h.
Where, a and b are the length of two parallel sides
h is the distance between the parallel sides.
- The integration of sinx is -cosx
- The value for cos(0) and cos(pi) can also be calculated using the COS function. Note that the angles are in radian.
Download the Practice Workbook
<< Go Back to Formula List | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!

