Method 1 – Volume Calculation of a Sphere
Volume of a Sphere = 4/3 * pi * r^3
Steps:
- We only need to know the radius of the sphere.
- Select a cell for the volume calculation (i.e. C7).
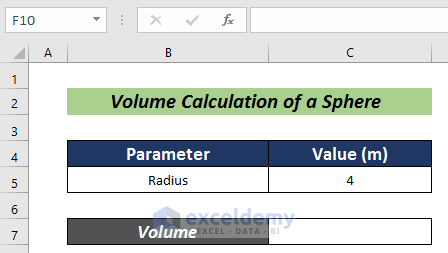
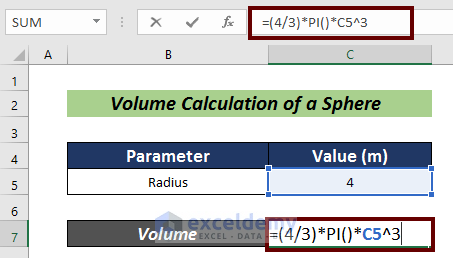
- Input the following formula in cell C7:
=(4/3)*PI()*C5^3Here, C5 represents the radius of the sphere in meters.
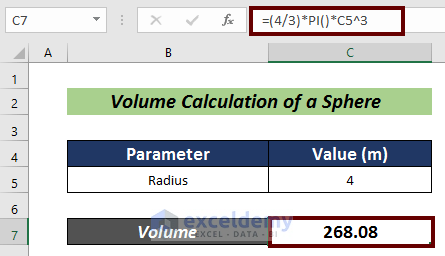
- Press Enter to have the volume of the sphere.
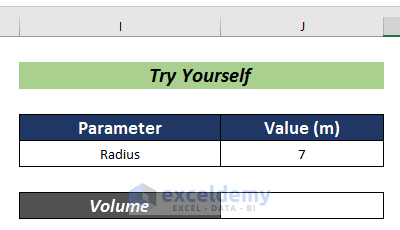
You can insert a custom value and check if the formula changes.
Method 2 – Volume Calculation of a Rectangular Solid
Volume of a Rectangular Solid= l * a * b
Steps:
- We need the length, width, and height of the solid in cells C5, C6, and C7.
- Choose a cell for the volume calculation (i.e. C9).
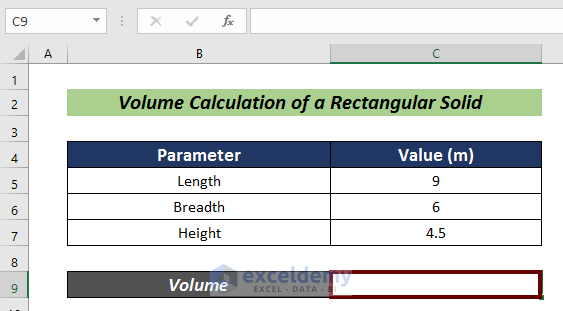
- Insert the following formula:
=C5*C6*C7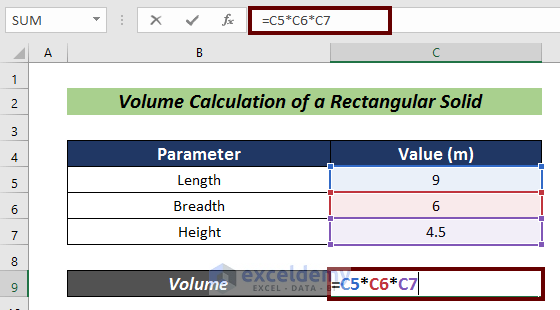
- Hit Enter.
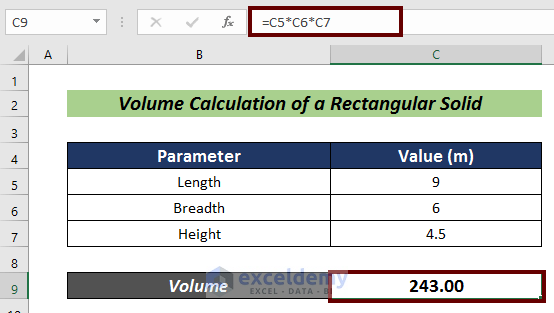
Try yourself in the following section.
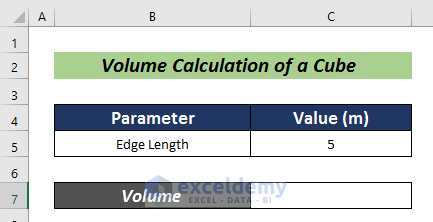
Method 3 – Volume Calculation of a Cube
Volume of a Cube= a^3
Steps:
- Insert the edge length of the cube in C5.
- Pick a cell for the calculation (i.e. C7).
- Insert the formula mentioned below:
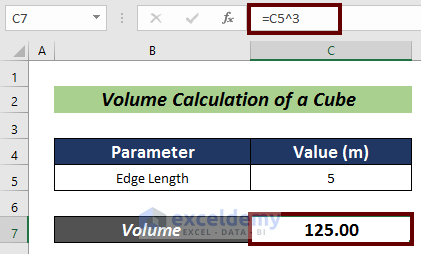
=C5^3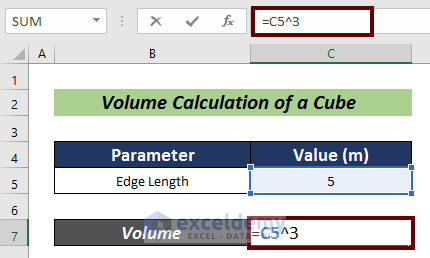
- Hit Enter.
You can practice here by yourself.
Method 4 – Volume Calculation of a Cylinder
Volume of a Cylinder = pi * r^2 * H
r = Radius of the base
h = Height
Steps:
- Put the radius and height of a cylinder in cells C5 and C6.
- Pick a cell for the volume calculation (i.e. C8).
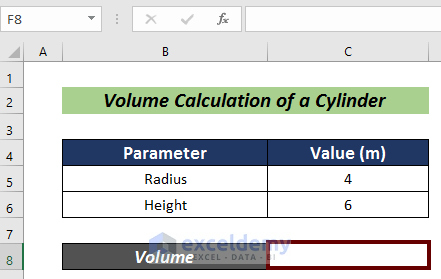
- Input the following formula:
=PI()*C5^2*C6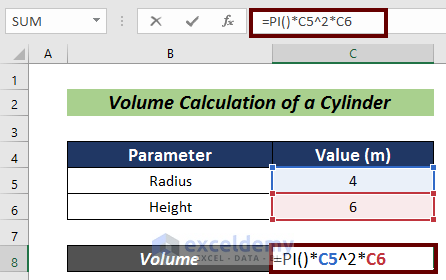
- Hit Enter.
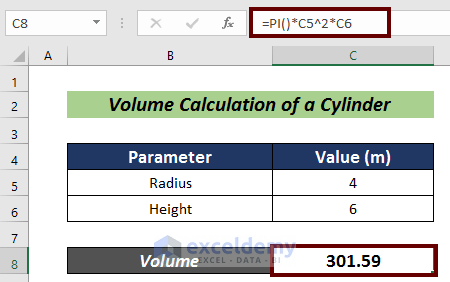
You can practice in the sample datasheet.
Method 5 – Volume Calculation of a Cone
Volume of a Cone = 1/3 * pi * r^2 * h
r = Radius of the base
h = Height of the cone
Steps:
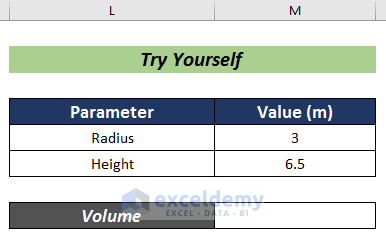
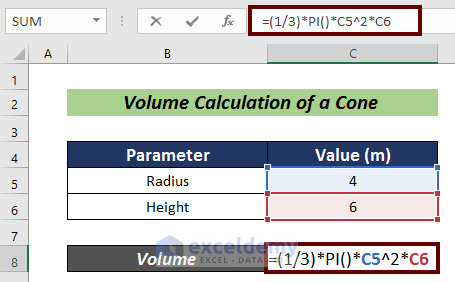
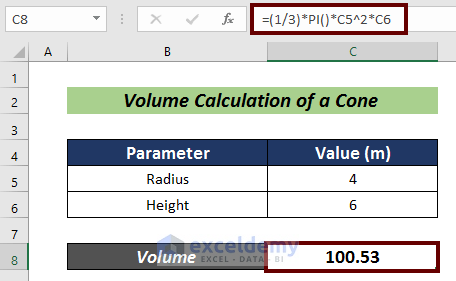
- Put the radius and height of a cone in cells C5 and C6.
- Choose a cell for the volume calculation (i.e. C8).
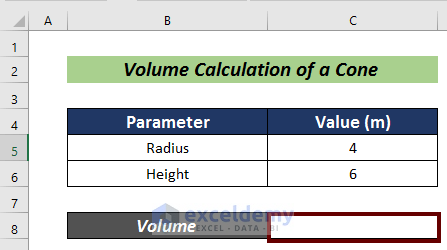
- Input the formula mentioned below:
=(1/3)*PI()*C5^2*C6- Press Enter.
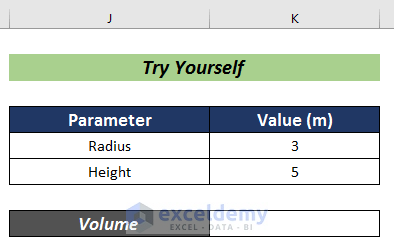
Try yourself in the practice section.
Method 6 – Volume Calculation of a Torus
Volume of a Torus = 2 * pi^2 * r^2 * R
r = inner radius of the cross-section
R = outer radius of the torus (distance from the center of the torus to the center of the cross-section)
Steps:
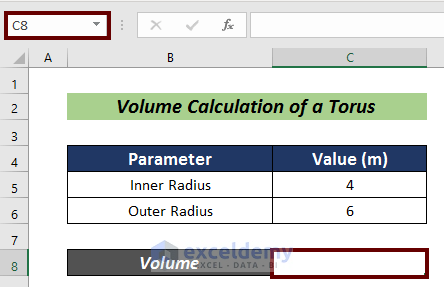
- Put the inner and outer radiuses of a torus in cells C5 and C6.
- Select a cell for the volume calculation (i.e. C8).
- Input the formula mentioned below:
=PI()*C5^2*2*PI()*C6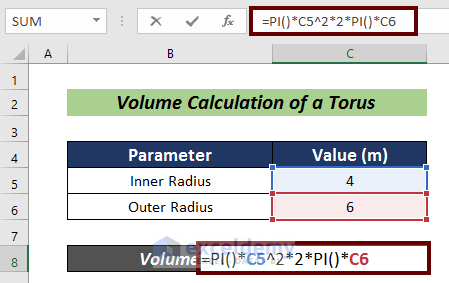
- Hit Enter.
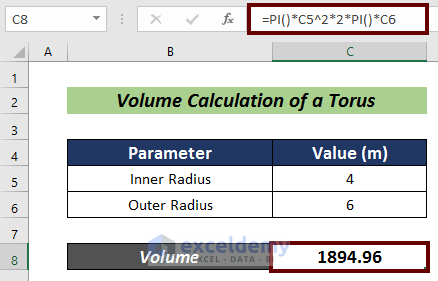
You can practice in the practice worksheet.
Method 7 – Volume Calculation of an Ellipsoid
Volume of an Ellipsoid = 4/3 * pi * a * b * c
a, b, and c are the lengths of the axes. A sphere will have equal axes.
Steps:
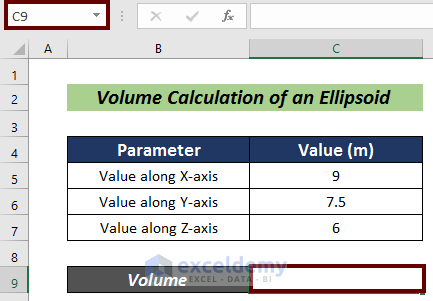
- Put the ellipsoid values a, b, and c, into cells C5, C6, and C7.
- Choose a cell for the volume calculation (i.e. C9).
- Insert the following formula:
=(4/3)*PI()*C5*C6*C7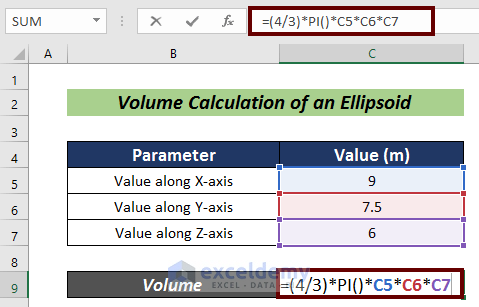
- Press Enter.
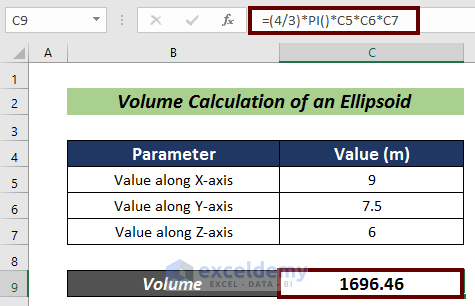
Use the practice section for testing.
Download the Practice Workbook
<< Go Back to Formula List | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!