You have to solve 2 linear equations for X and Y.
3X – Y = 5
4X – Y = 2
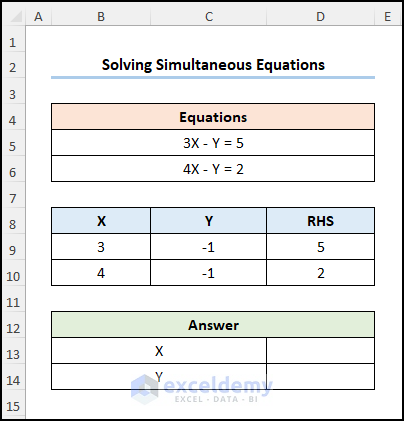
Method 1 – Utilizing the MMULT and the MINVERSE Functions
Steps:
- Select D13:D14 and enter the following formula.
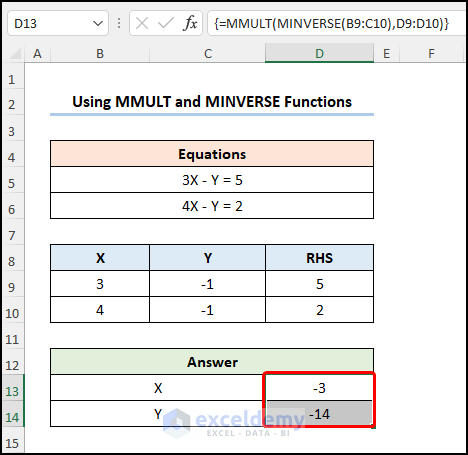
=MMULT(MINVERSE(B9:C10),D9:D10)
Here, the B9:C10 and D9:D10 represent the X and Y coefficients and the constant values on the right-hand side of the equation.
Note: Press CTRL + SHIFT + ENTER since this is an array formula.
Formula Breakdown:
- MINVERSE(B9:C10) → returns the inverse matrix for the matrix stored in an array. Here, the function returns the values of the inverse matrix.
- =MMULT(MINVERSE(B9:C10),D9:D10)→ returns the matrix product of two arrays. Here, the function multiplies the inverse matrix array with the values on the RHS and gives the output.
This is the output.
Method 2- Solving Simultaneous Equations with an Excel Add-in
Steps:
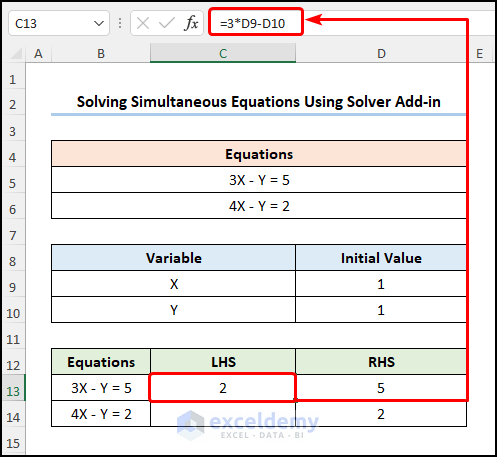
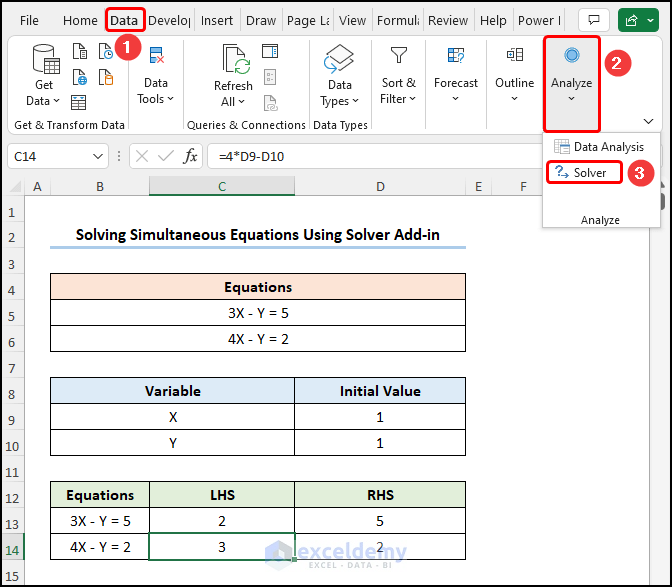
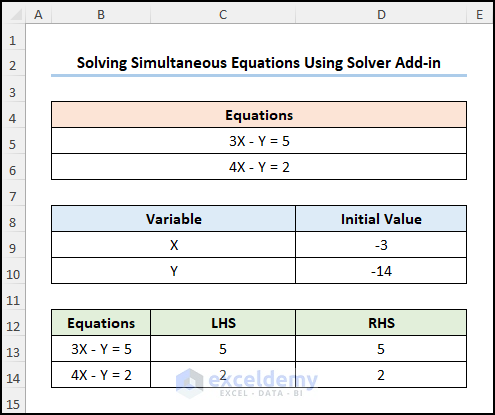
- In C13 cell >> enter the LHS of the linear equation:
=3*D9-D10
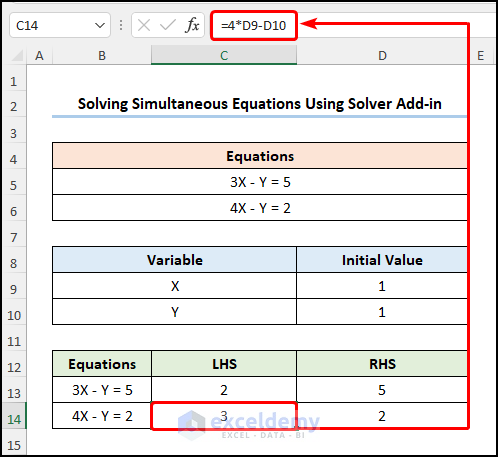
Here, D9 and D10 indicate the Initial Values of X and Y.
- Enter this formula in C14.
=4*D9-D10
- Click the File tab.
- Choose Options.
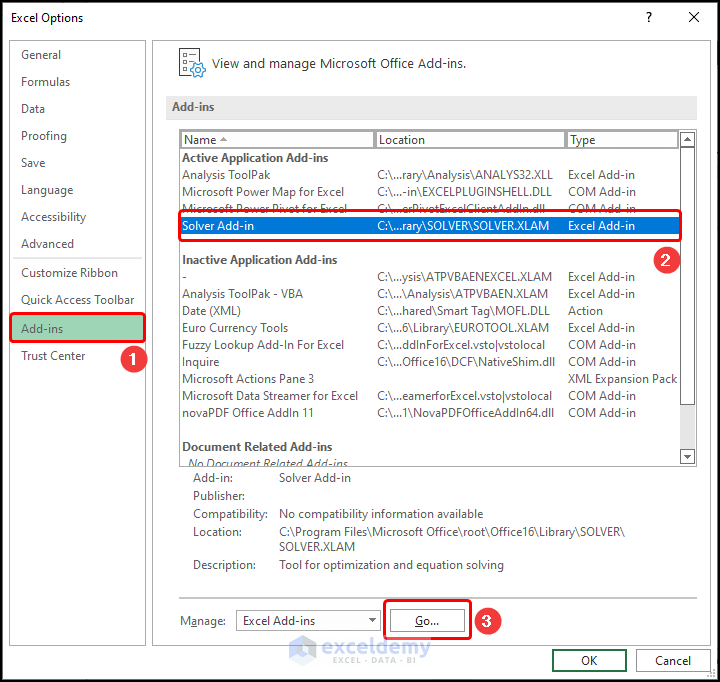
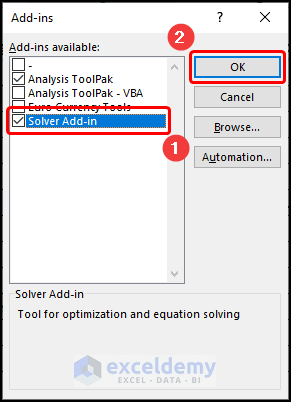
- Click Add-ins >> select Solver Add-in >> click Go.
In the Add-ins dialog box:
- Choose Solver Add-in >> click OK.
The Solver Add-in is added.
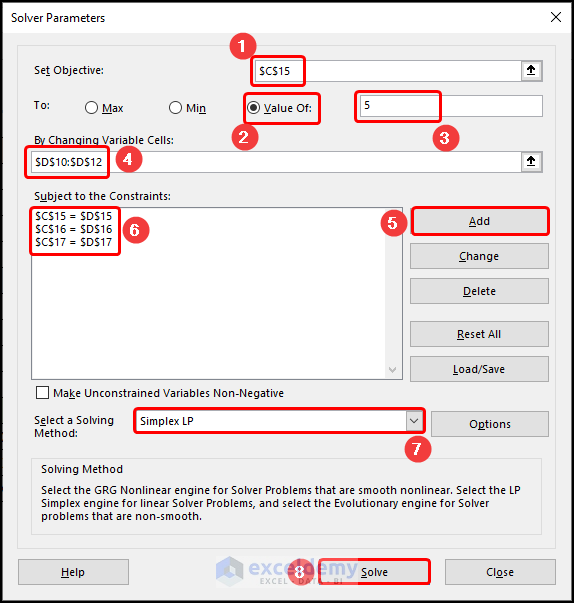
- Go to the Data tab >> click Analyze >>choose Solver.
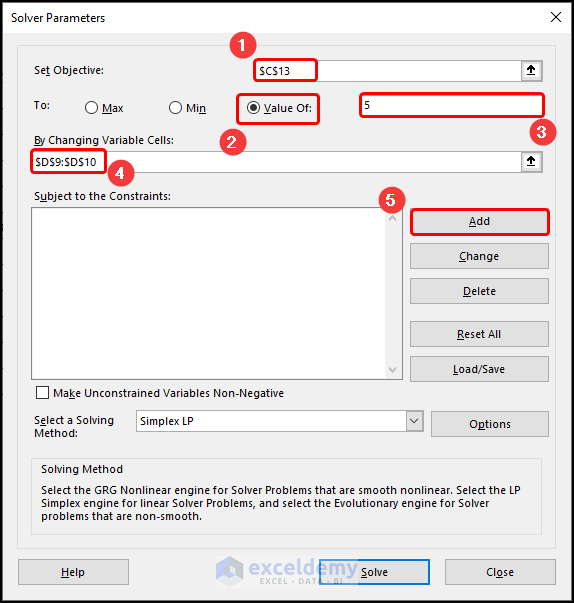
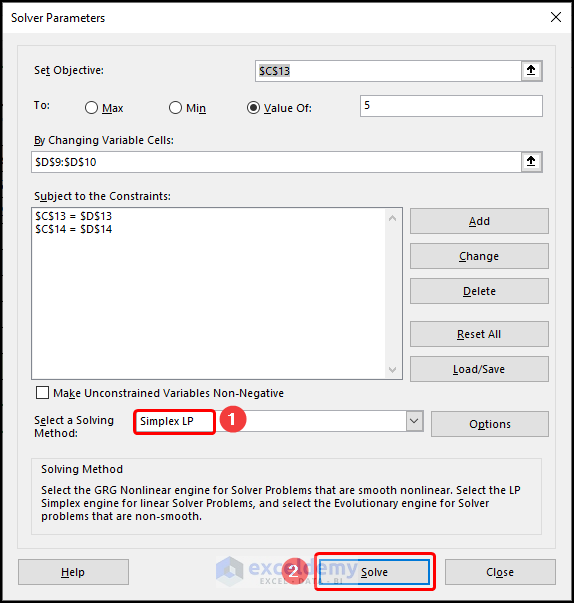
- In Set Objective, enter C13.
- In To options, select Value Of and enter the value of the constant, here, 5.
- In By Changing Variable Cells, enter C8:C9.
- Click Add to set the constraints.
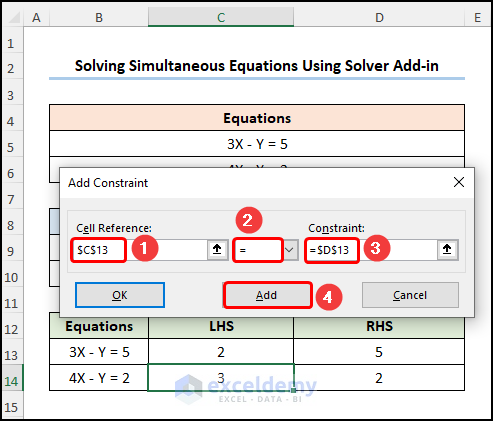
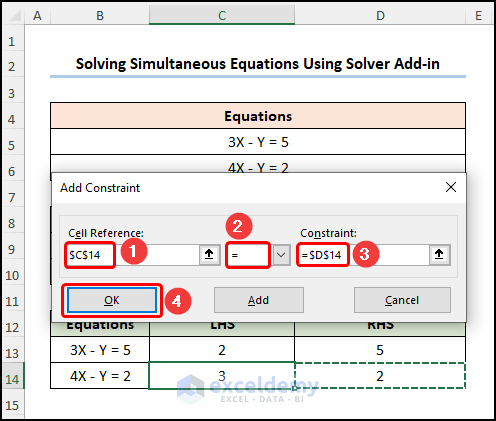
In the Add Constraint window:
- Enter C13 in Cell Reference.
- Choose an equal sign (=) from the dropdown list >>enter D13 in the Constraint field >> Click Add.
- Repeat the same procedure to add a second constraint and click OK.
- Choose Simplex LP in Select a Solving Method.
- Click Solve.
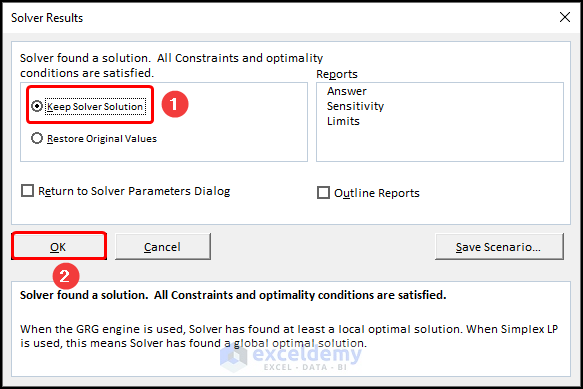
- Check Keep Solver Solution and click OK.
This is the output.
Read More: How to Solve 2 Equations with 2 Unknowns in Excel
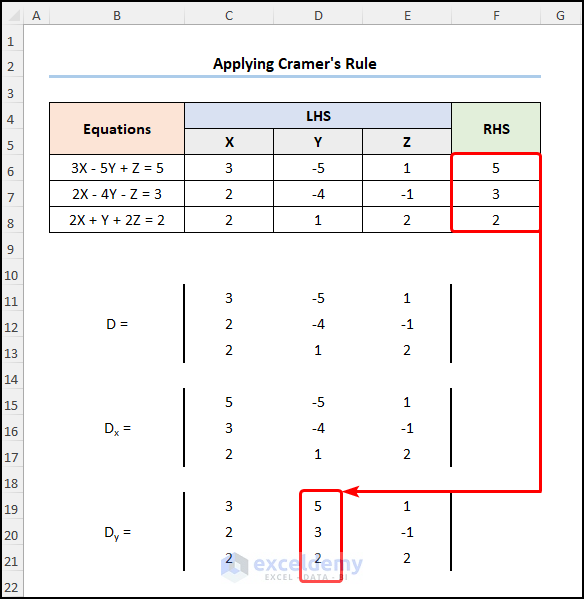
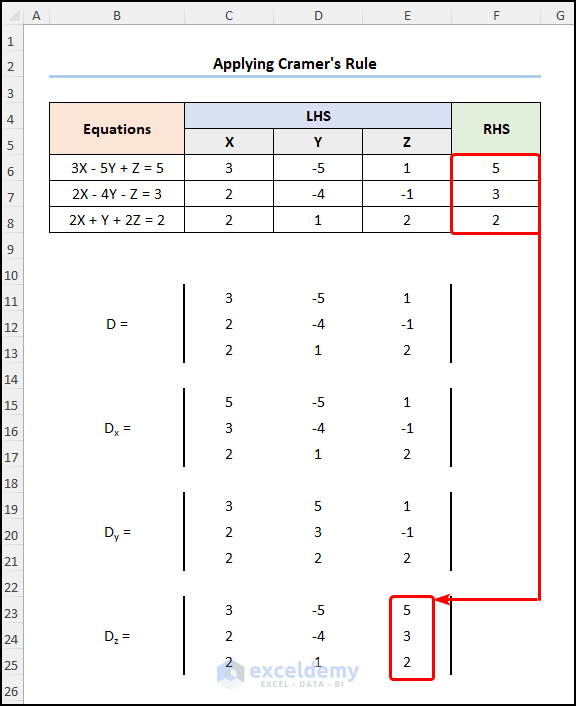
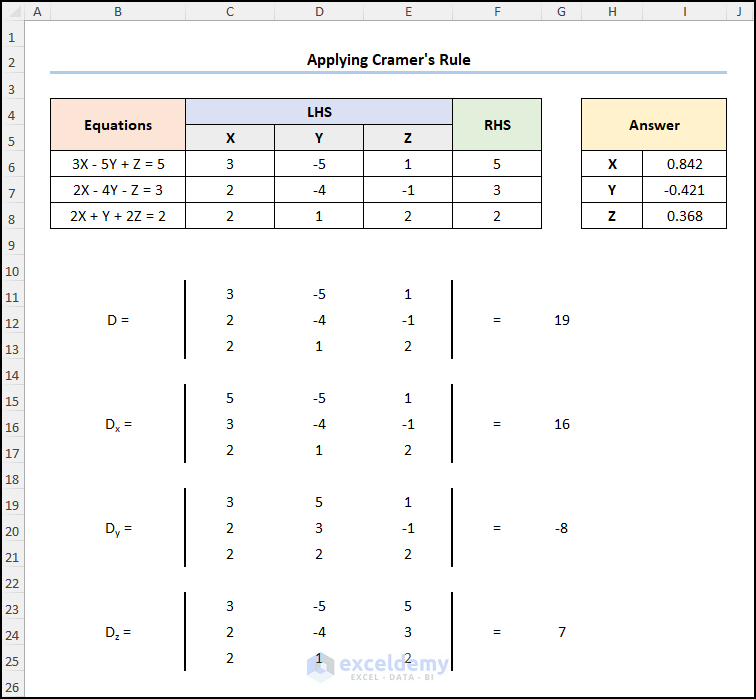
Method 3 – Solve Simultaneous Equations with 3 Variables Applying the Cramer’s Rule
Steps:
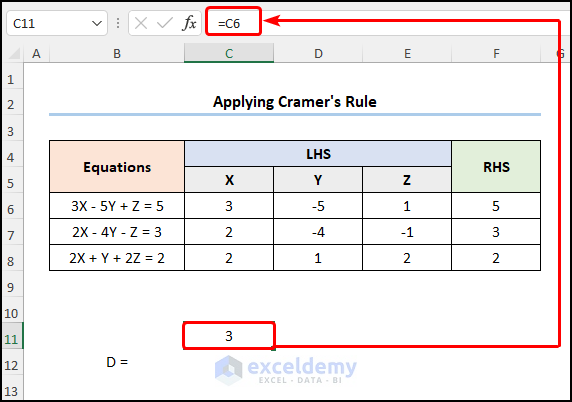
- In C11, enter the C6 cell reference.
=C6
C6 cell points to the coefficient of X.
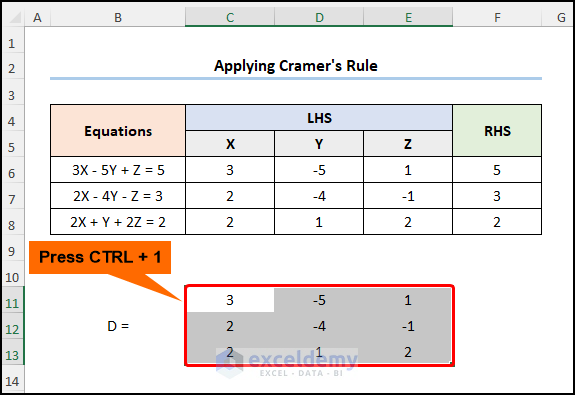
- Enter all values and press CTRL + 1.
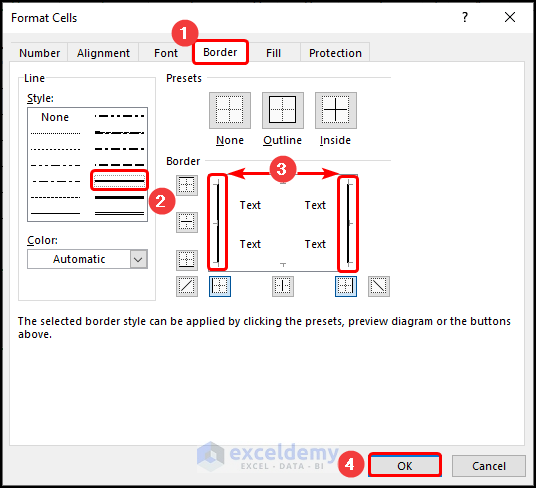
In Format Cells:
- Select Border and follow the steps shown in the image below.
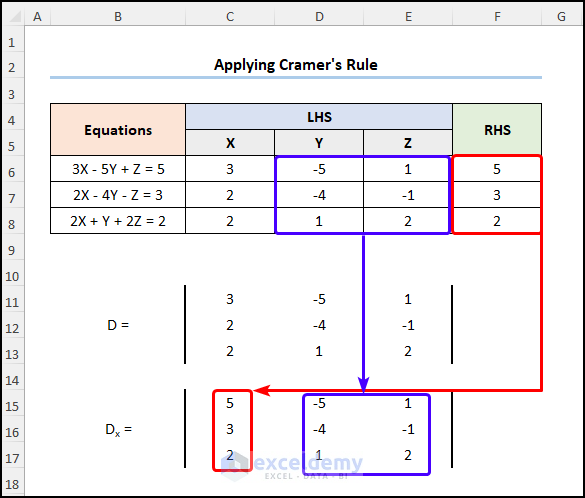
- Go to C15 >> enter the values in the RHS column.
- Enter the coefficients of Y and Z in the next two columns.
- Enter the values for Dy in the second column.
- Enter the values for Dz in the third column.
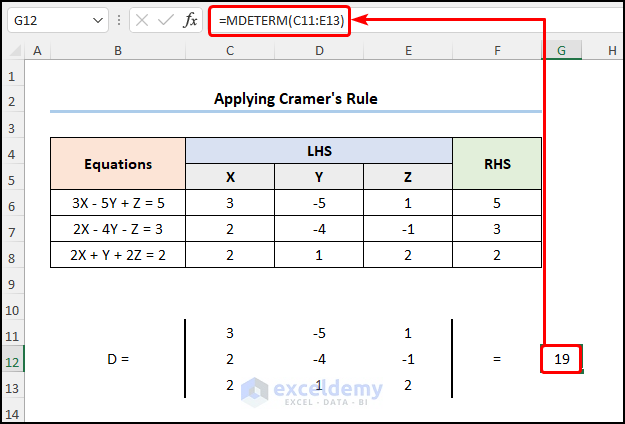
- Go to G12 and enter the formula below.
=MDETERM(C11:E13)
the MDETERM function calculates the determinant of the C11:E13 array.
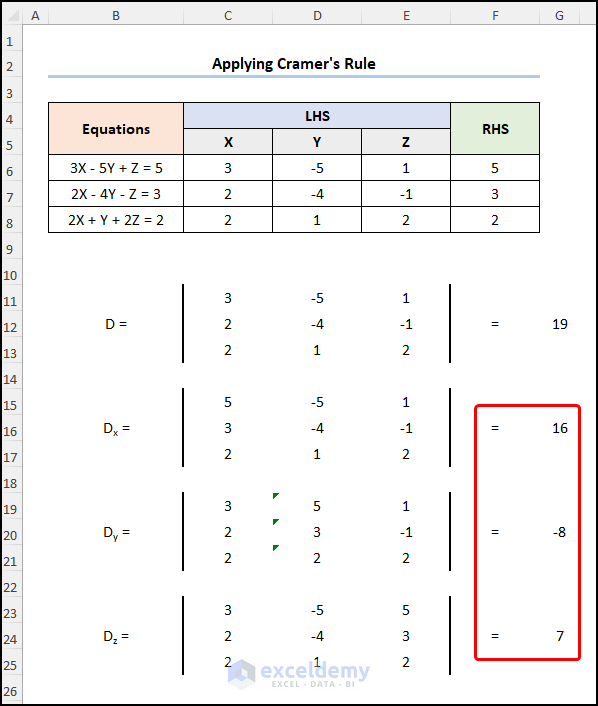
- Enter the determinants of x, y, and z.
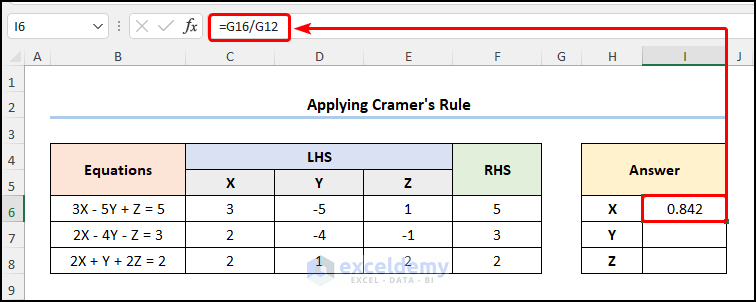
- Go to I6 cell and enter the formula below.
=G16/G12
G16 and G12 represent the values of Dx and D.
This is the output.
Read More: How to Solve an Equation for X When Y is Given in Excel
How to Solve Quadratic Equations in Excel
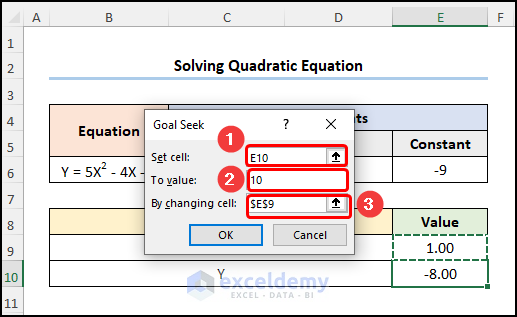
Steps:
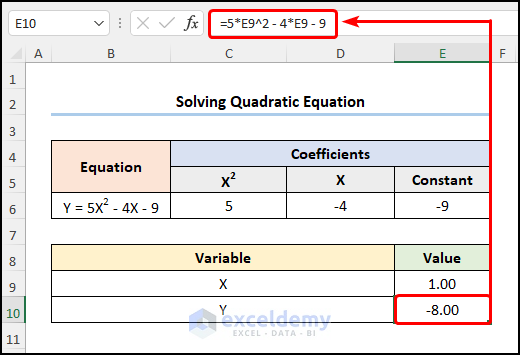
- Go to E10 and enter the quadratic equation.
=5*E9^2 - 4*E9 - 9
E9 refers to the values of X.
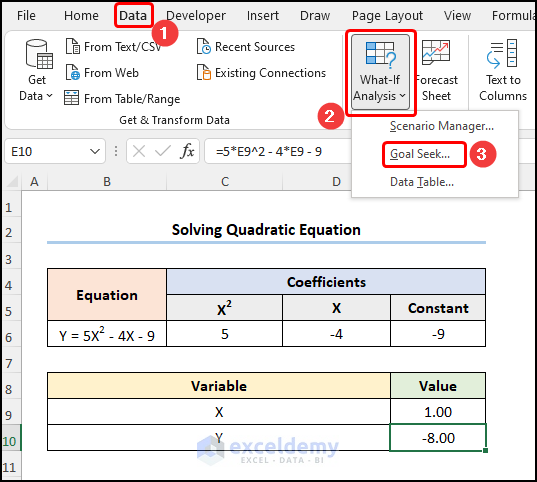
- Go to the Data tab >> click What-If Analysis >> select Goal Seek.
In Goal Seek:
- In Set cell, enter E10 >> in To value, enter 10 >> in By changing cell >> select E9.
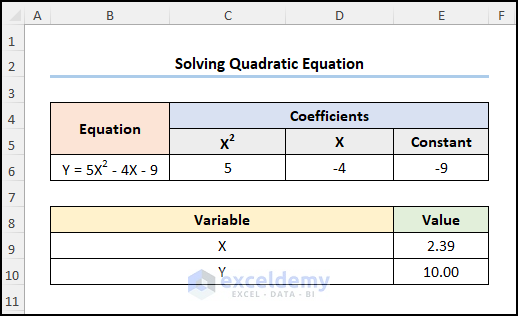
This is the output.
Read More: How to Solve Polynomial Equation in Excel
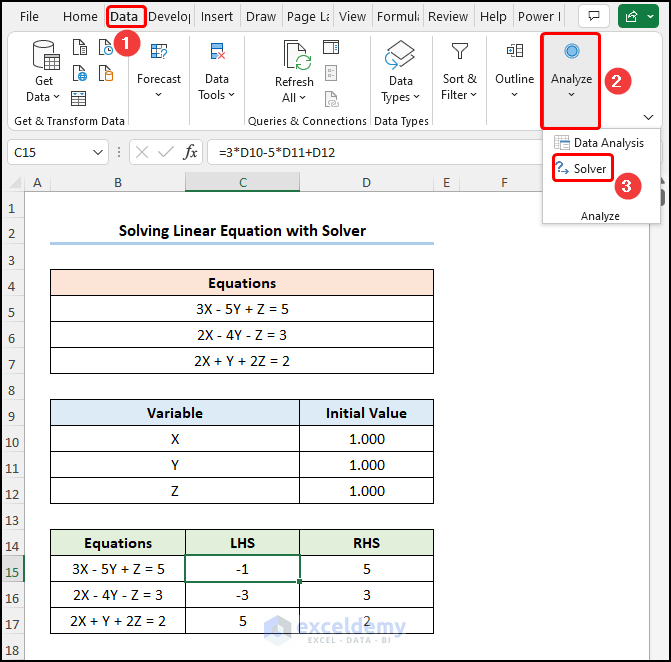
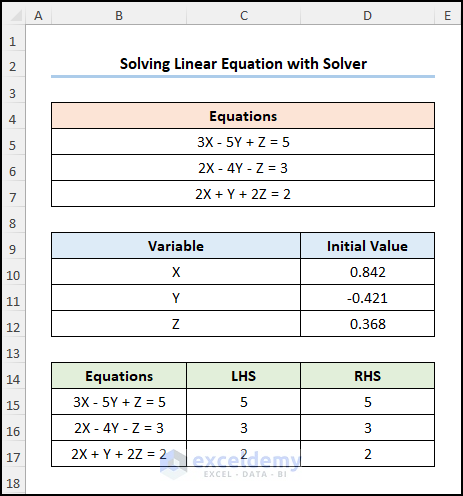
How to Solve Linear Equations in Excel Using the Solver
Steps:
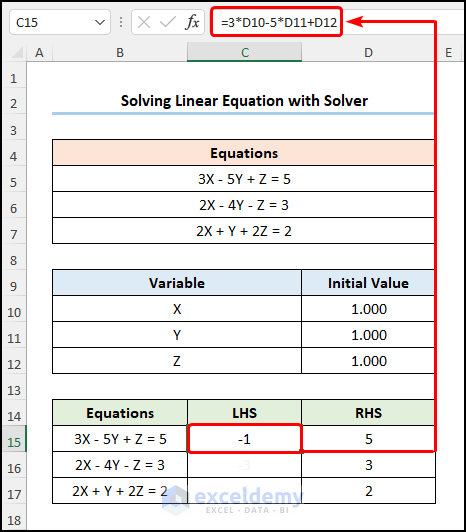
- Go to C15 and enter the linear equation.
=3*D10-5*D11+D12
D10, D11, and D12 indicate the Initial Values of X, Y, and Z.
Repeat the same process for the other two equations.
- Go to the Data tab >> click Analyze >> choose Solver.
- Follow the steps described in Method 2.
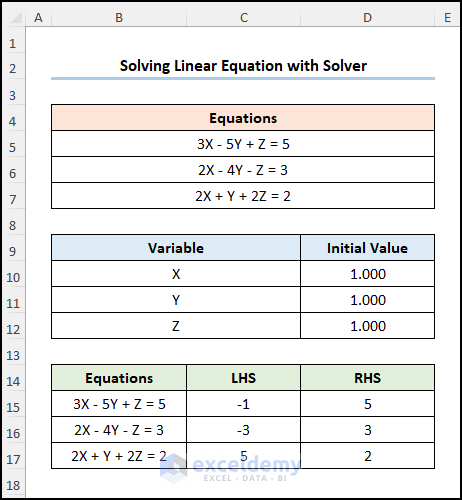
This is the output.
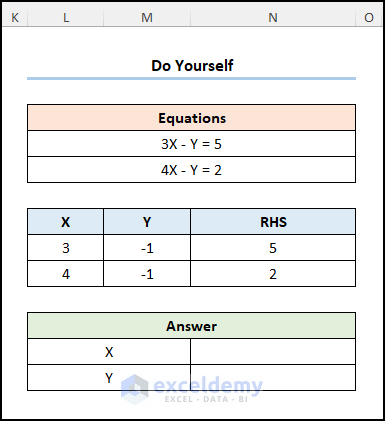
Practice Section
Practice here.
Download Practice Workbook
Download the practice workbook.
Related Articles
- How to Solve for x in Excel
- How to Solve Algebraic Equations with Multiple Variables
- How to Solve System of Equations in Excel
- How to Solve Differential Equation in Excel
- How to Solve Exponential Equation in Excel
- How to Solve Cubic Equation in Excel
- How to Solve Colebrook Equation in Excel
- How to Solve Quadratic Equation in Excel VBA
<< Go Back to Excel Solve Equation | Excel Solver Examples | Solver in Excel | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!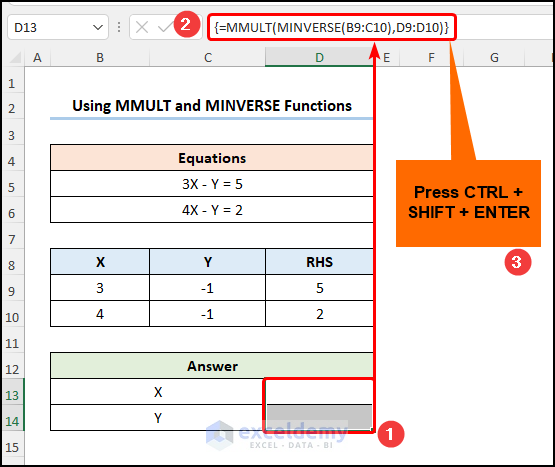
Hi,
I am trying to solve linear equations with multiple unknowns. Sample below. Problem is I have only one equation with multiple unknows
19.6=a+0.0124x+0.0304y+0.175z
I need a excel function to give possible values for the variables in above equation. Anyone knows how to do it?
P.S: I am not looking for solutions where we have three unknowns and hence we cant solve with less than three questions. I need to know what are the possible (not unique) values that satisfies the above equation
Thanks
Need more lessons on solving quadratic and linear equations.
Very helpful! Thank You
thank you so much it was really helpful 😀
Glad to know that it helped you.
Thanks and regards
Kawser Ahmed