How to Perform Mixed Integer Linear Programming in Excel

Excel is the most widely used tool for dealing with massive datasets. We can perform myriads of tasks of multiple dimensions in Excel. In this article, I will explain how you can perform mixed integer linear programming in Excel. The entire process is going to be divided into some easy steps for your convenience.

Here is an overview of this article.

Introduction to Mixed Integer Linear Programming

Mixed Integer linear programming is a type of mathematical method that consists of integer variables and linear objective functions and equations. The mixed-integer linear programming has both continuous and integer variables. With the help of linear programming, we can determine the minimum or maximum outcome of a given problem with some conditions. It is a tool that can be used to achieve a way to apply limited resources in the best possible manner. All types of linear programming include some main factors. They are given below:

Decision Variables: We determine the decision variables that minimize or maximize the objective function.
Objective Function: This is a function that helps us to determine the decision variables. It expresses the relation between the result and the variables.
Constraints: Constraints are also functions that denote different conditions on possible solutions.

Perform Mixed Integer Linear Programming in Excel: Step-by-Step Procedures

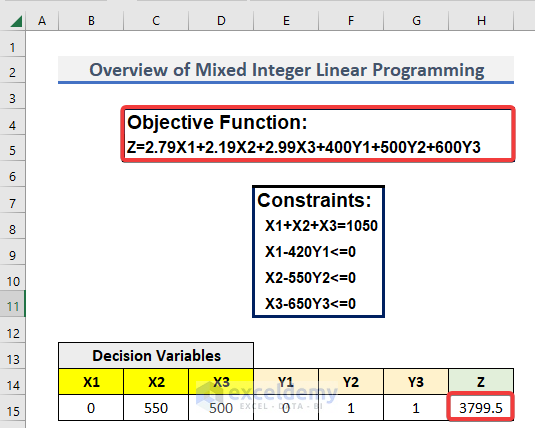
Let’s first understand the problem. I will explain the steps with the help of this problem. First of all, you have to set your objective function and the constraints.

I have assumed the one shown below.

Objective Function

Z=2.79X₁+2.19X₂+2.99X₃+400Y₁+500Y₂+600Y₃

Constraints

X₁+X₂+X₃=1050
X₁-420Y₁<=0
X₂-550Y₂<=0
X₃-650Y₃<=0

Here, X₁, X₂, and X₃ are integers. On the other hand, Y₁, Y₂, and Y₃ are binary numbers. Also, we need to find the minimum value of Z.

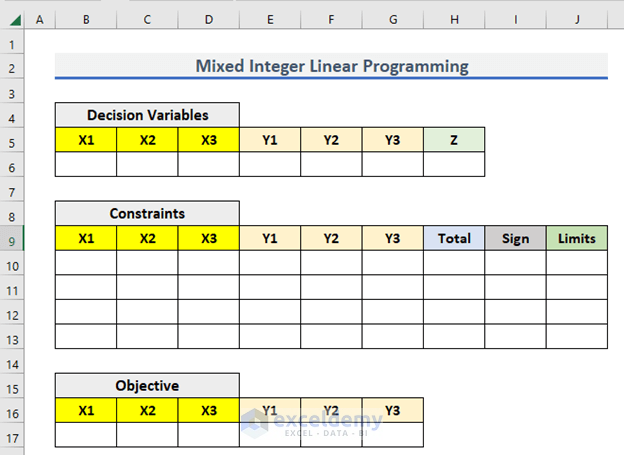
Step 1: Insert Details

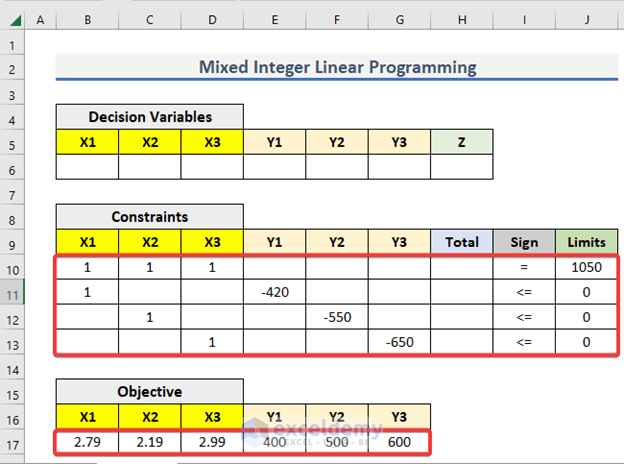
Once you set the equations, you have to input the details in an Excel sheet. You can create three separate tables like below. The tables should include,

Decision Variables
Constraints
Objective

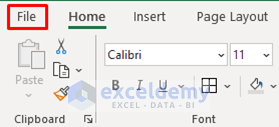
Step 2: Load Solver Add-in in Excel

Then, we need to load the Solver Add-in in Excel. To do so,

Click on the File tab.

After that, select Options from the left–bottom corner of the screen.

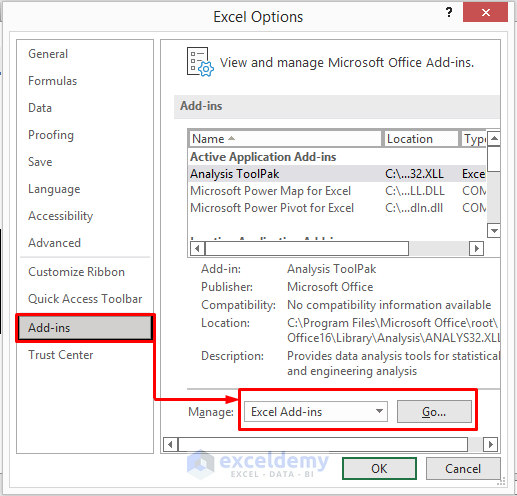
It will open the Excel Options.
In the Excel Options window, select Add-ins.
Then, select Excel Add-ins and click on Go in the Manage.

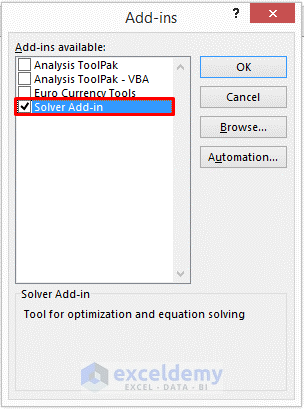
An Add-ins message box will pop up.
Check Solver Add-in and select OK from the message box.

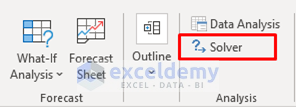
Finally, you will see the Solver feature in the Analysis section of the Data tab.

Step 3: Type Mixed Co-Efficients of Objective Function and Constraints

The next step is to write down the coefficients of objective function and constraints.

Write down the coefficients of the objective function in the B17:G17 range.
Similarly, input the coefficients of the constraints in the B6:J13 range.
Keep the Total column empty for now.
After this step, your worksheet should look like this.

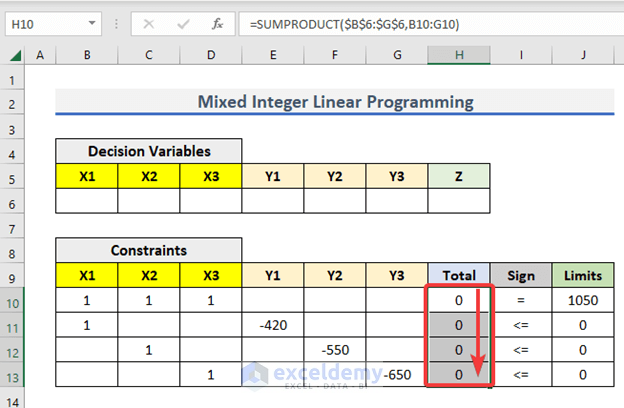
Step 4: Calculate Totals

Now we will take care of the Total column. To measure this, we will use the SUMPRODUCT function.

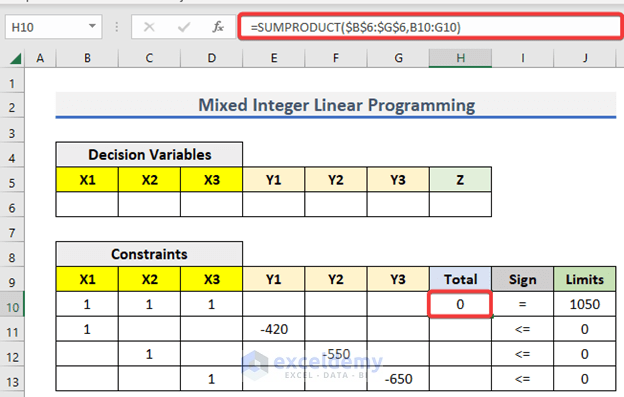
First of all, go to H10 and write down the following formula

=SUMPRODUCT($B$6:$G$6,B10:G10)

Then, press ENTER to get the output.

Then, use Fill Handle to AutoFill up to H13.

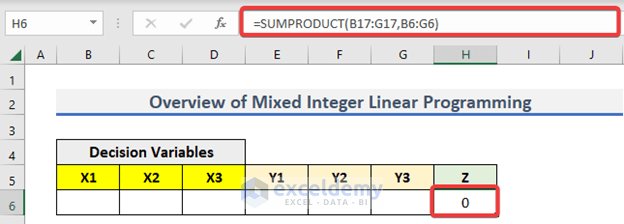
Step 5: Measure Dependent Variable of Objective Function

In this step, we will calculate the value of Z. The function to be used is again the SUMPRODUCT function.

Go to H6 and write down the following formula.

=SUMPRODUCT(B17:G17,B6:G6)

After that, press ENTER to get the output.

Step 6: Apply Solver Add-in

Now, you have to apply the Solver Add-in. To do so,

To begin with, go to the Data tab.
Then, select Solver.

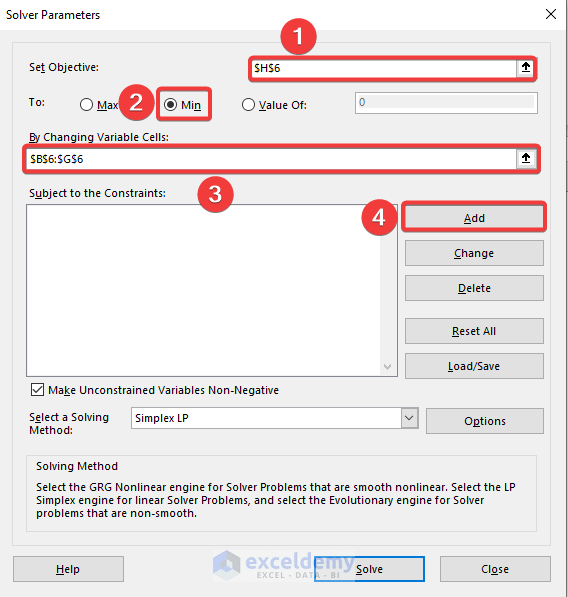
A Solver Parameters window will appear.
Then, set the objective H6 to be minimum.
After that, set the variables that Excel is going to change.
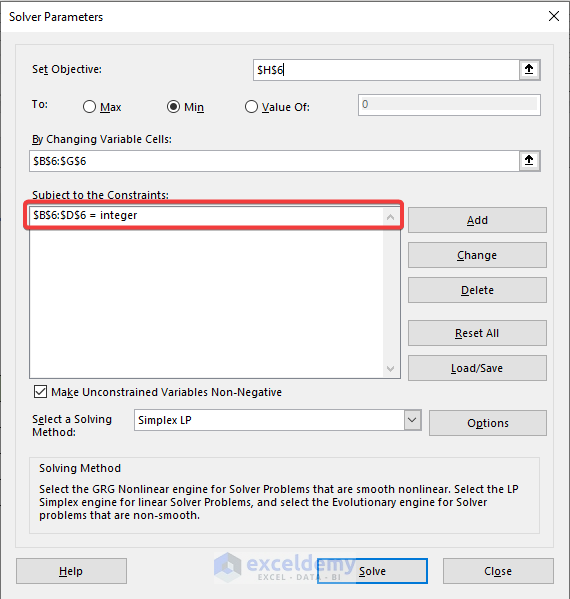
Then, select Add to set the constraints.

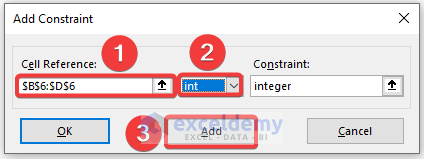
After clicking Add, an Add Constraint box will appear.
Then, set the Cell Reference and the condition from the drop-down list.
Finally, click Add.

You will see that Excel has added a constraint.

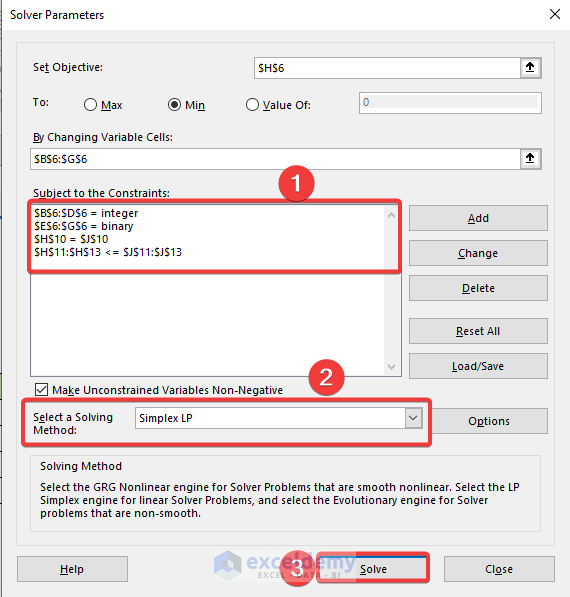
Similarly, add other constraints.
Then, select a solving method.
Finally, click Solve.

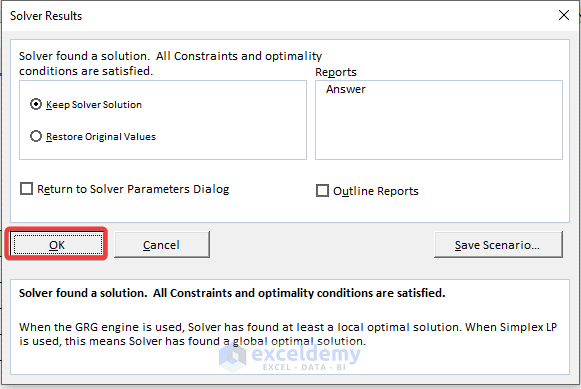
The Solver Result box will appear then.
Click OK.

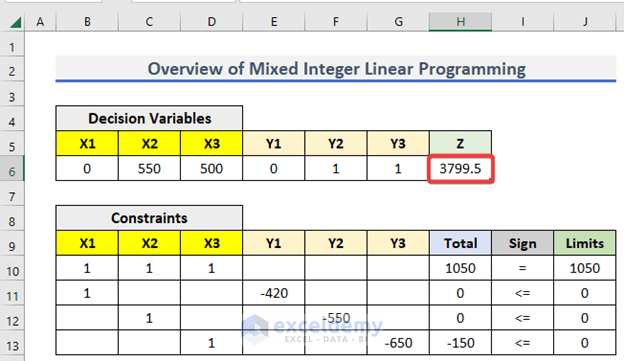
Step 7: Show Final Output

After clicking OK, Excel will solve the problem for you. The outputs are shown below.

Download Practice Workbook

Download this workbook and practice while going through the article.

Mixed Integer LP.xlsx

Conclusion

In this article, I have demonstrated how to perform mixed integer linear programming in Excel. I hope it helps everyone. If you have any suggestions, ideas, or feedback, please feel free to comment below.

<< Go Back to Excel Linear Programming | Solver in Excel | Learn Excel

Get FREE Advanced Excel Exercises with Solutions!