How to Find Optimal Solution with Linear Programming in Excel

Linear Programming is very useful in practical life in terms of resource optimization. In case you are looking for detailed steps on how to find the optimal solution in linear programming excel, this article may really help you. So, let’s move on to the process.

Find Optimal Solution with Linear Programming in Excel: Step-by-Step Procedures

We have used the Solver tool to find the optimal solution in linear programming. Solver is a Microsoft Excel tool that uses techniques from operations research in order to find optimal solutions for various kinds of decision problems. How to add Solver to the menu bar is also explained. How to find optimal solutions in linear programming in Excel is implemented in this article in 6 easy steps.

Step 1: Activating Solver Add-in

In this step, we will see how to enable the Solver option which is essential to start the process.

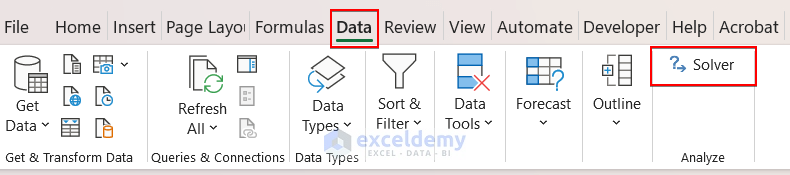
Generally, you will find the Solver option in the Data tab. It is on the Excel Ribbon which is at the top of an Excel sheet.

If the option is not available, follow the steps to add Solver in your Data tab.

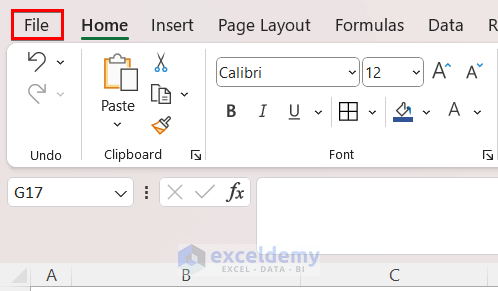
First, click on the File menu which is marked below.

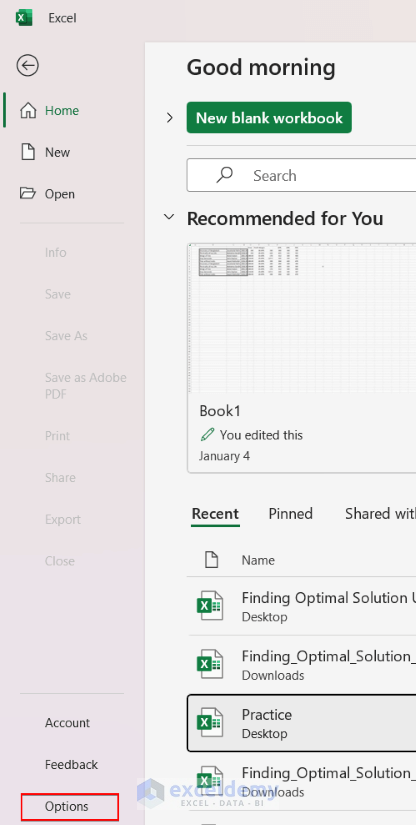
You will find Options at the bottom.

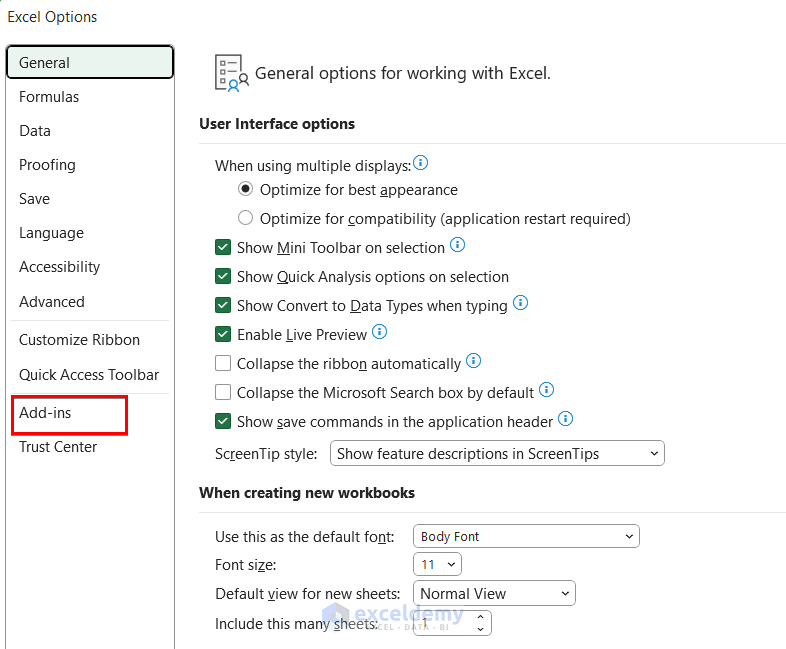
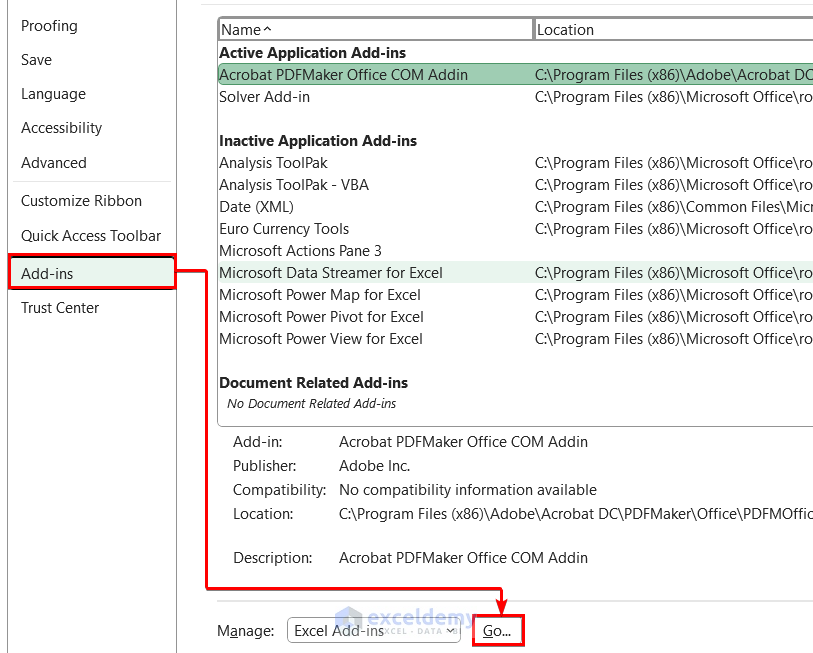
Then, select the Options button and a tab will open like the following one. From this, you have to select Add-ins.

Consecutively, select the Go option beside Excel Add-ins.

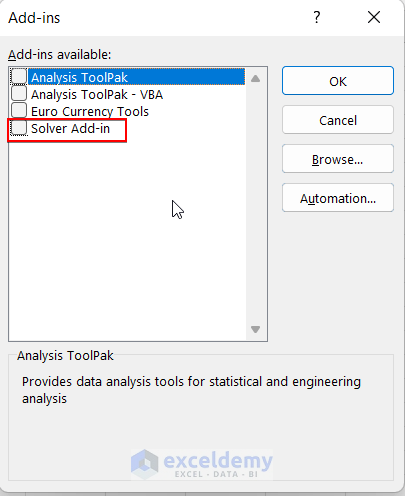
Later, the Add-ins available will appear.

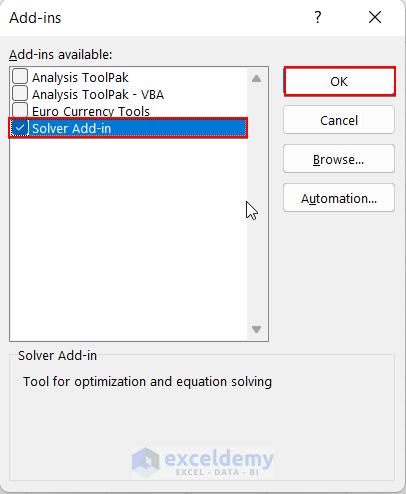
Lastly, put a tick beside the Solver Add-in option and hit the OK button.

As a result, you have successfully activated the Solver option in your Data Tab.

Step 2: Presenting Problem Data in a Table

This step summarizes your practical problem into a data table which will be further used to find the optimized result.

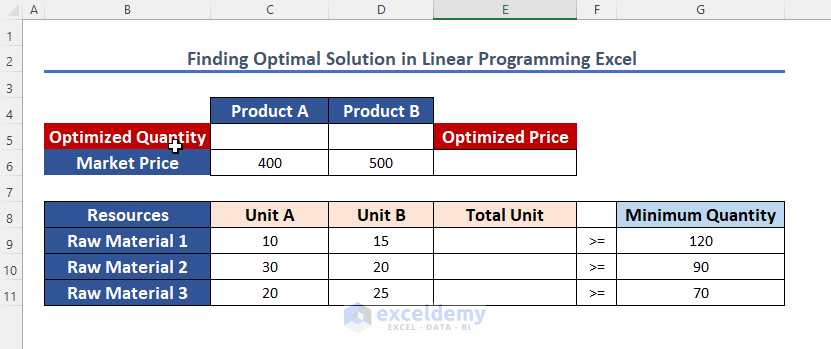
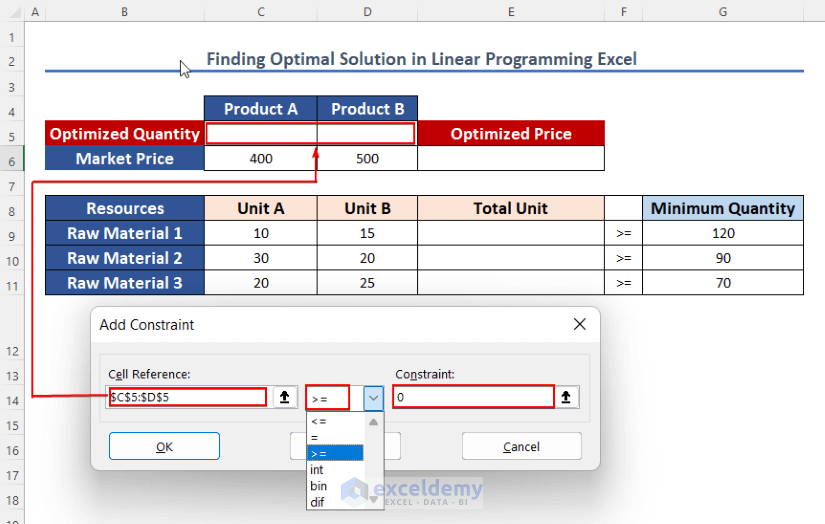
Suppose a manufacturer is producing two products (Product A and Product B) that need the same three types of raw materials.
Let’s name them Raw Material 1, Raw Material 2, and Raw Material 3.
To produce Product A, they need 10 units of Raw Material 1, 30 units of Raw Material 2, and 20 units of Raw Material 3. And for Product B, they use these materials in 15, 20, and 25 units.
A minimum amount of each material is to be used mandatorily. Minimum quantities of Raw materials 1, 2, and 3 are 120, 90, and 70.
The market price of Product A is 400 $ and Product B is 500 $.
Now, we have to determine the optimized Quantity of Products A and B so that the company will gain maximum profit.

Step 3: Applying Formulas for Linear Programming

After getting our table ready, we want to determine the optimal quantity so that we can get the maximum price. Therefore, we will apply some formulas to the cells to get the total price.

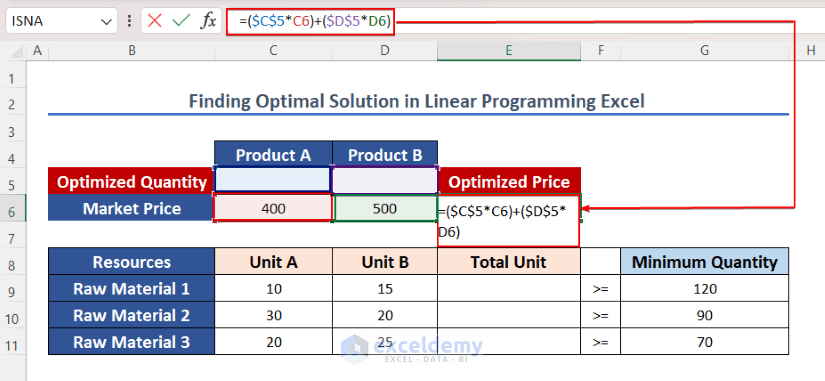
Initially, put down the formula in cell E6.

=($C$5*C6)+($D$5*D6)

This formula is mainly based on multiplying the unit price with the quantity. And by adding both prices, you will get the total price in cell E6.

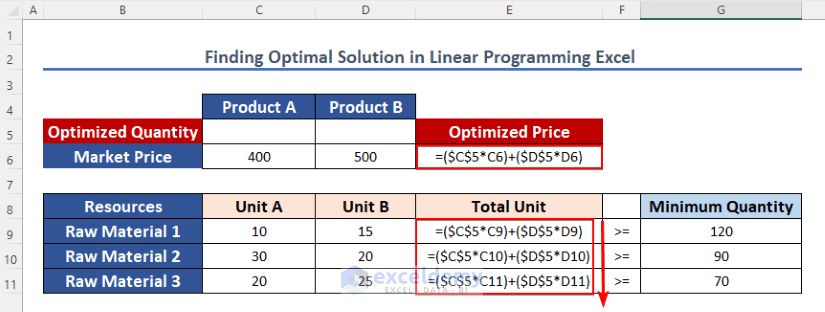
Afterward, copy the formula down to cells E9 to E11 by using the AutoFill tool.

Step 4: Using Solver Add-in to Determine Optimized Value

This is the most important step where Solver is used. Go through the steps carefully.

At this point, click on the Data menu and select Solver from the Analyze menu.

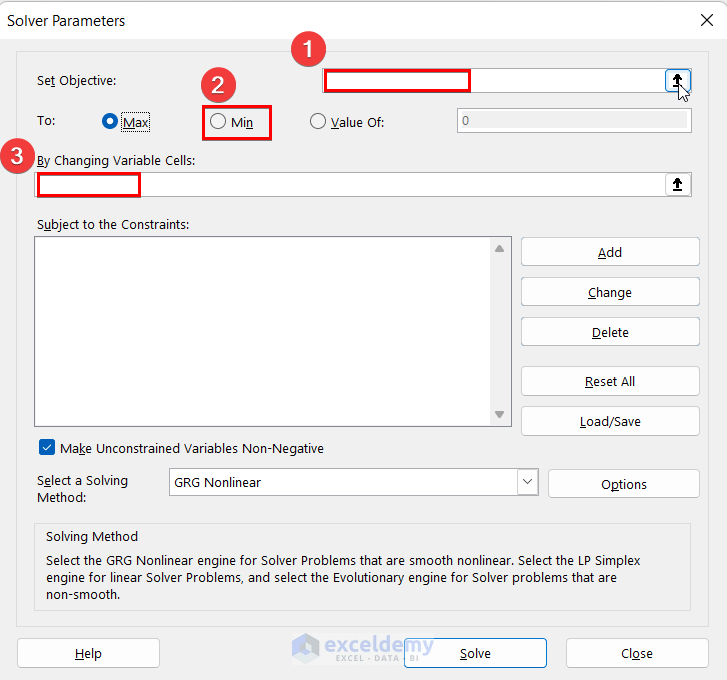
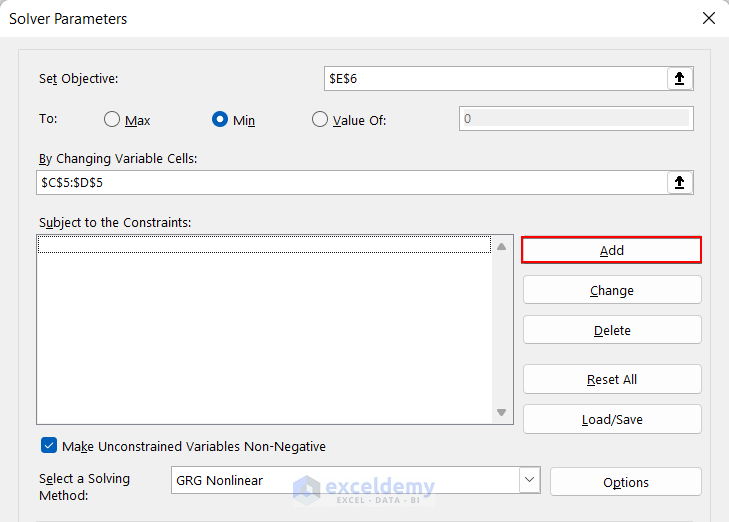
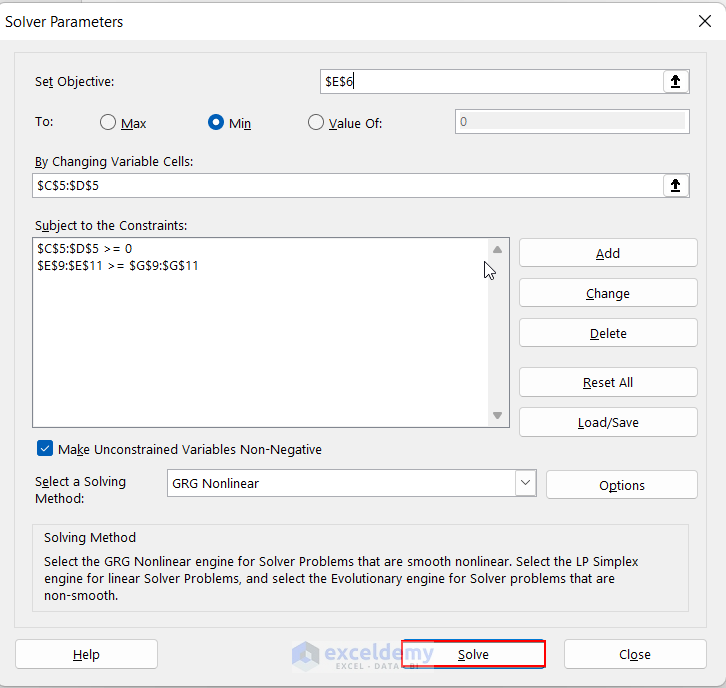
After selecting the Solver option these Solver Parameters will appear.

Fill up these 3 options accordingly.
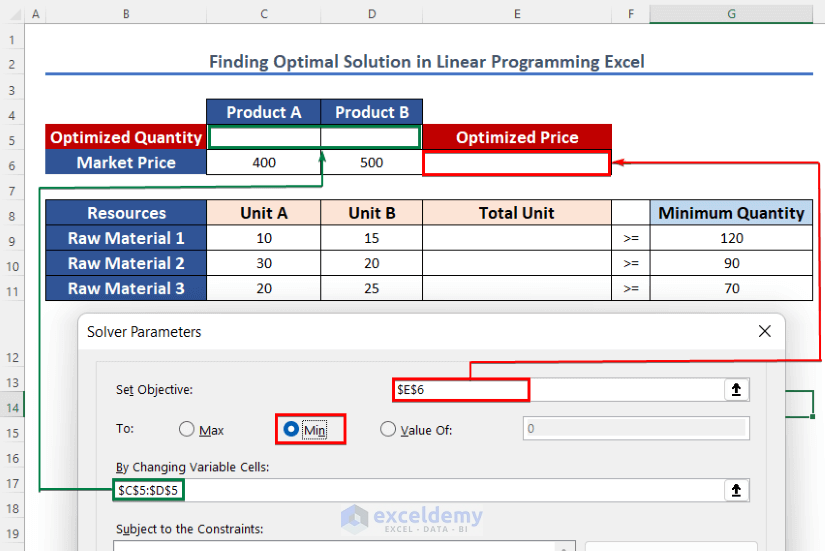
The set objective is cell $E$6.
As we want the minimum amount of materials to gain maximum profit, so Min option is selected here.
Variable cells are $C$5:$D$5. In these cells, you will get an optimized quantity of products.

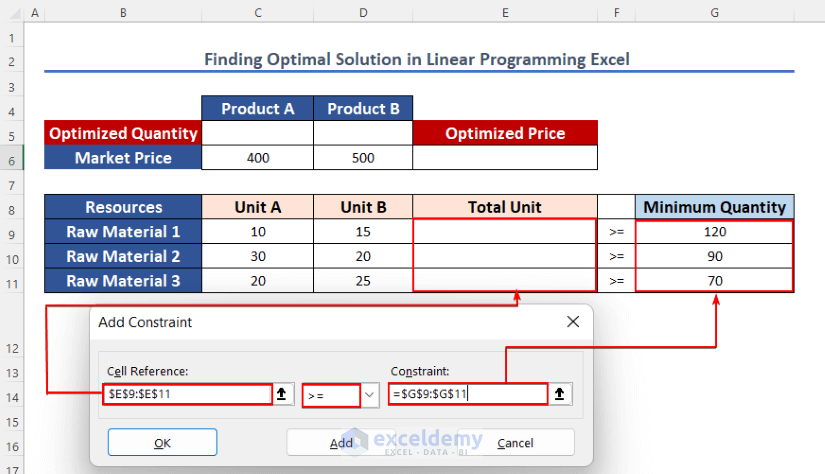
Step 5: Adding Subject to the Constraints

The Solver needs some Subject to the constraints to make a decision. In this step, we will provide the constraints Suitably.

Right now, below the Subject to the Constraints box, Add the subject to the constraints.

Therefore, fill up Cell Reference, Inequality sign, and Constraint.

Cell Reference is $C$5:$D$5, inequality is >= and Constraint will be 0. Because X, and Y cannot be zero.

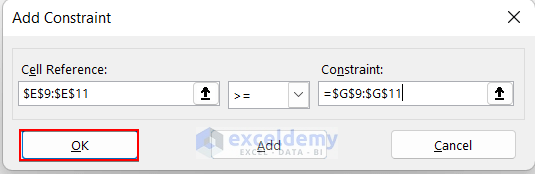
Lastly, add one more Constraint by clicking on Add.

Cell Reference is $C$5:$D$5, inequality is >= and Constraint is $G$9:$G$11.

After including these two Constraints, hit the OK button.

Step 6: Finding Optimal Solution to Maximize Profit

Step 6 will give you the final result by solving according to your given Solver Parameters.

In conclusion, select Solve.

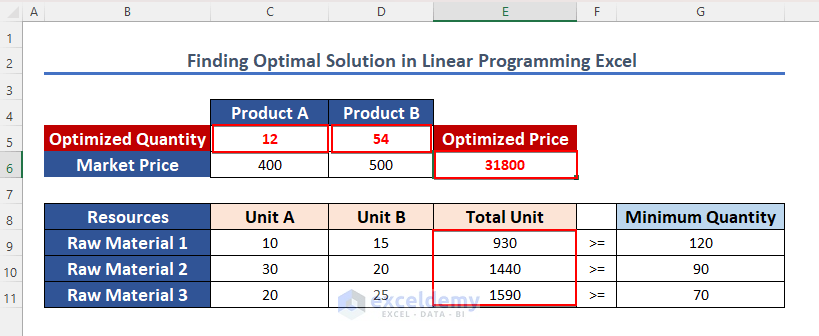
As a result, we determined the Optimized Quantity of Product A and B which is 12 and 54.
Moreover, the Total required unit of each raw material and the optimized Price is provided here.

Download Practice Workbook

Finding Optimal Solution Using Linear Programming.xlsx

You may download the following Excel workbook for better understanding and practice it by yourself.

Conclusion

This article shows how to find the optimal solution in linear programming in Excel. The solver is used to find out the desired output. We have tried to show each step so that it will be easy to solve your problem in a short time. If you face any problems regarding this article, please let us know in the comment section.

<< Go Back to Excel Linear Programming | Solver in Excel | Learn Excel

Get FREE Advanced Excel Exercises with Solutions!