Here’s an overview of a matrix in Excel and the functions that create inverse matrices.
Download the Practice Workbook
What Does an Inverse Matrix Mean in Excel?
A matrix’s inverse, represented as A-1, has the following characteristics:
A * A^-1 = A^-1 * A = I,
The Identity Matrix I is a square matrix with ones on its major diagonal and zeroes everywhere else.
How to Calculate an Inverse Matrix in Excel: 3 Simple Methods
Method 1 – Using the MINVERSE Function to Calculate an Inverse Matrix in Excel
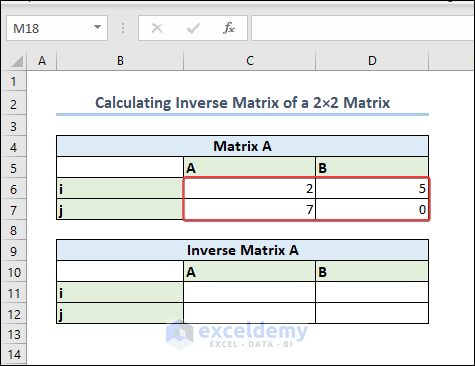
Case 1.1 – Calculate the Inverse Matrix of a 2×2 Matrix
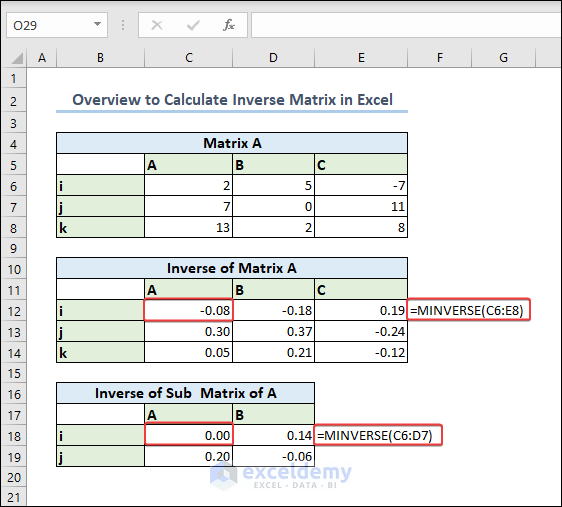
We have a 2-by-2 matrix (2×2) in the dataset range C6:D7.
- Insert the following formula in a new cell and hit Enter.
=MINVERSE(C6:D7)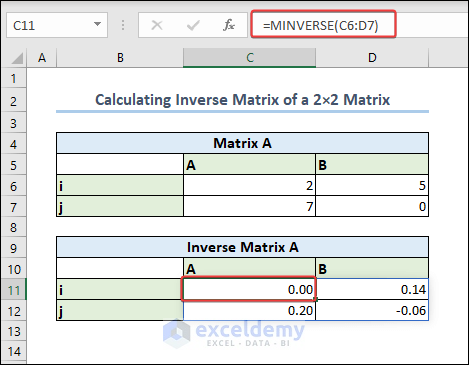
- For older versions of Excel, you have to press Ctrl + Shift + Enter instead of Enter because it’s an array formula.
Case 1.2 – Calculate the Inverse Matrix of a 3×3 Matrix
- We put the matrix in C6:E8.
- Apply the following formula:
=MINVERSE(C6:E8)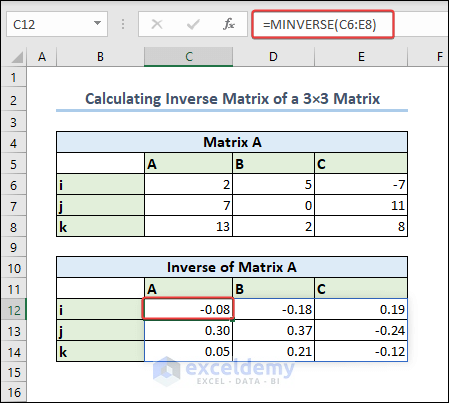
Case 1.3 – Calculate the Inverse Matrix of a 4×4 Matrix
- If the matrix is in C6:F9, use the following formula a few rows below.
=MINVERSE(C6:F9)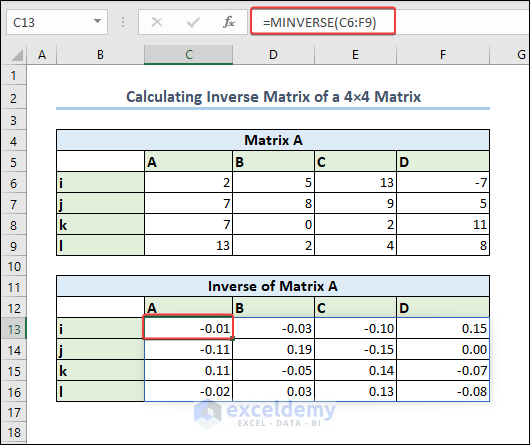
Method 2 – Using a Manual Formula to Determine the Inverse Matrix
We will calculate the Adjoint Matrix and then divide it by the Determinant of the Matrix to get the Inverse.
- We put the matrix in C6:E8 (3×3 matrix).
- Apply the following formula in a cell to get the Adjoint Matrix. We put it in B11.
=MINVERSE(C6:E8) * (MDETERM(C6:E8) *(-1) ^ (ROW() + COLUMN()))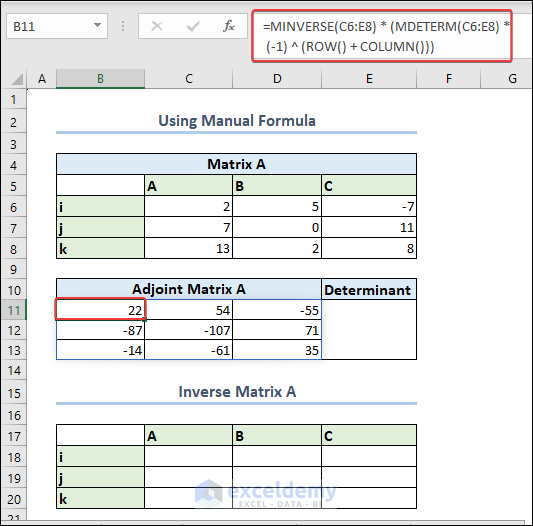
- Insert the following formula next to the new matrix to get the Determinant. We used the cell E11.
=MDETERM(C6:E8)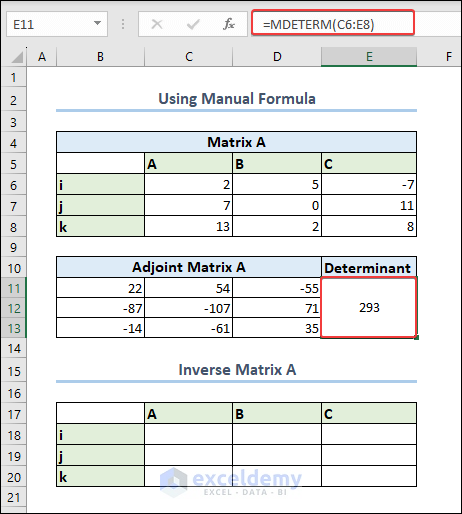
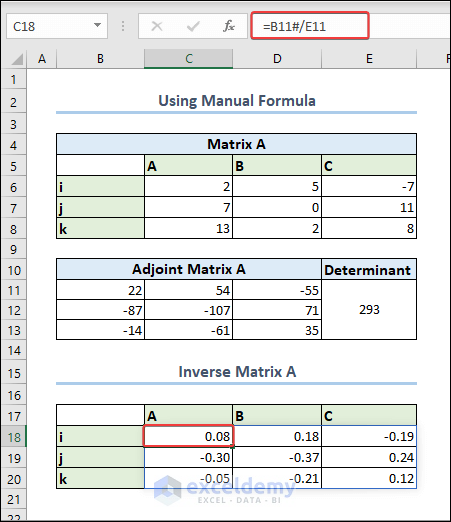
- Use the following formula in a cell to get the desired inverse matrix:
=B11#/E11The values here are used from the cells we set for the Adjoint Matrix and the Determinant, respectively. Since the B11 cell contains a range of values that is displayed over a 3×3 array, the result is a similar 3×3 matrix.
Method 3 – Creating a VBA User-Defined Function to Find the Inverse Matrix in Excel
- Open the VBA Window and Insert a New Module. Follow the link if you don’t know the way already.
- Use the following code in a new module.
Code:
Function inverseMatrixA(rng As Range) As Variant
Dim matrix() As Variant
Dim inverse() As Variant
Dim size As Integer
Dim i As Integer, j As Integer
Dim app As Object
size = rng.rows.Count
ReDim matrix(1 To size, 1 To size)
ReDim inverse(1 To size, 1 To size)
' Convert the range values to a 2D array
matrix = rng.Value
' Create an instance of the Excel Application object
Set app = CreateObject("Excel.Application")
' Disable alerts and screen updating to speed up the calculation
app.DisplayAlerts = False
app.ScreenUpdating = False
' Use the MINVERSE function of the Excel Application object to calculate the inverse
inverse = app.WorksheetFunction.MInverse(matrix)
' Enable alerts and screen updating
app.DisplayAlerts = True
app.ScreenUpdating = True
' Clean up and release the Excel Application object
Set app = Nothing
' Return the inverse matrix
inverseMatrixA = inverse
End Function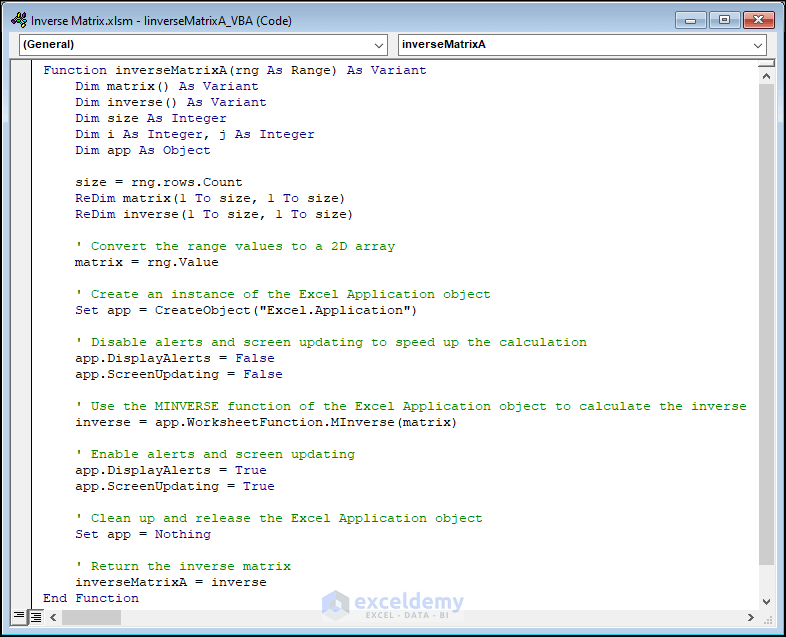
Code Breakdown:
- The function takes a range (rng) as input and declares variables for the matrices, size, and loop counters.
- The size of the matrix is determined by the number of rows in the input range.
- Arrays (matrix and inverse) are initialized with the appropriate dimensions based on the matrix size.
- The values of the input range are assigned to the matrix array.
- An instance of the Excel Application object (app) is created.
- Alerts and screen updating in Excel are disabled to improve performance.
- The MINVERSE function of the Excel Application object is used to calculate the inverse matrix, and the result is assigned to the inverse array.
- Alerts and screen updating in Excel are enabled again.
- The Excel Application object is released by setting it to Nothing.
- The function returns the inverse matrix as the output.
- Save the file.
- Use the created custom function in the worksheet to get the inverse matrix.
=inverseMatrixA(C6:E8)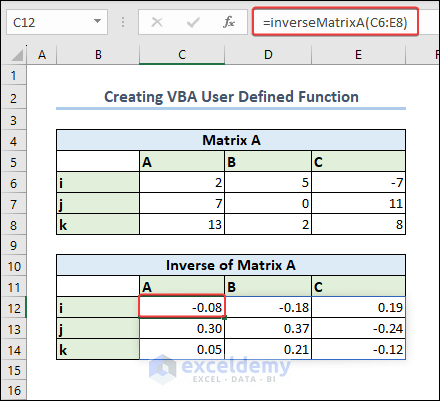
How to Do Inverse Matrix Multiplication to Find an Identity Matrix in Excel?
We will multiply a matrix with its inverse matrix to get the Identity Matrix.
- Create a dataset with a matrix in C6:E8.
- Find its inverse matrix in C13:E15 by following one of the methods above.
- Use the MMULT function to get the identity matrix:
=MMULT(C6:E8,C13:E15)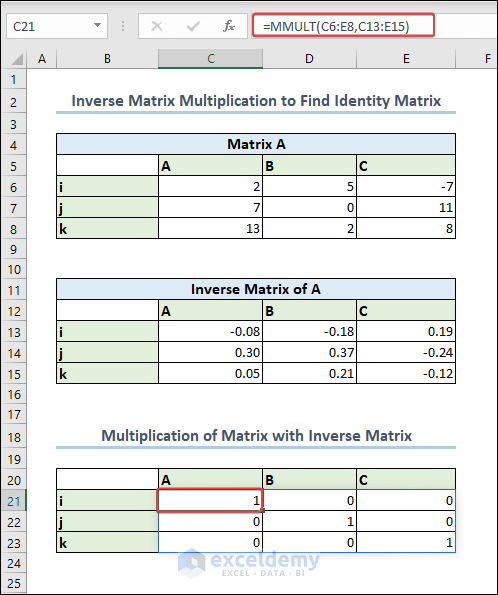
Frequently Asked Questions
What happens if the matrix cannot be inverted?
When using the MINVERSE function in Excel to try to find the inverse of a non-invertible matrix, an error such as #VALUE! or #NUM! will appear. A matrix with a determinant of 0 or which isn’t a square matrix doesn’t have an inverse.
Is it possible to locate the inverse matrix in Excel using VBA?
The calculations required to find the inverse matrix can be done by a VBA MInverse function. The function accepts a matrix as an argument, runs the necessary computations, and outputs the inverse matrix.
Is the inverse matrix unique?
Every invertible matrix has a unique inverse matrix. The inverse’s matrix inverse is the original matrix.
Things to Remember
- Save the workbook as a .xlsm file after inserting any VBA code.
- Be careful about using absolute and normal cell references.
- Only a square matrix is a valid input for an Inverse Matrix.


