In statistical analysis, covariance is an analysis of the relationship between changes in one variable and changes in another. It’s a metric for determining how close two variables are to one another. We perform the analysis in Excel by creating a matrix in the columns and computing the covariances. In this tutorial, we will show you how to calculate the covariance matrix in Excel.
How to Calculate Covariance Matrix in Excel: 3 Quick Steps
Covariance refers to the measurement of how one variable defers to another. Clearly, it’s a necessary evaluation of the deviation between two variables. Furthermore, the variables do not have to be dependent on one another. The formula for calculating covariance is represented in the following image.
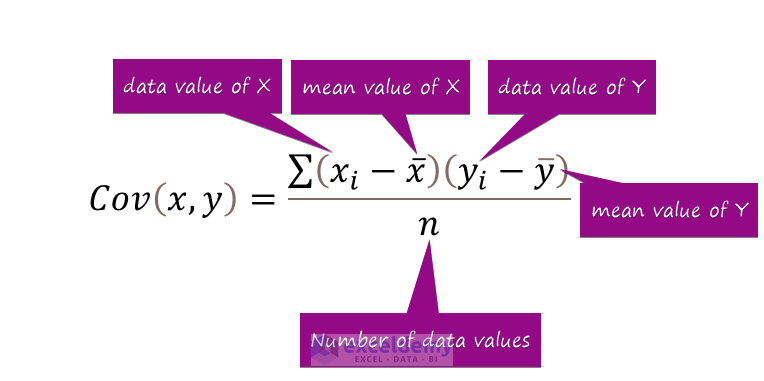
Xi = Data value of the first category
Yi = Data value of the second category
XÌ„ = Mean data Value of the first category
Ȳ = Mean data Value of the second category
n = Total number of data values
In the steps that follow, we’ll create two matrices with two categories each and use the covariance command in Excel to calculate the deviations. We’ll use the Data Analysis ribbon from the Data tab to do this.
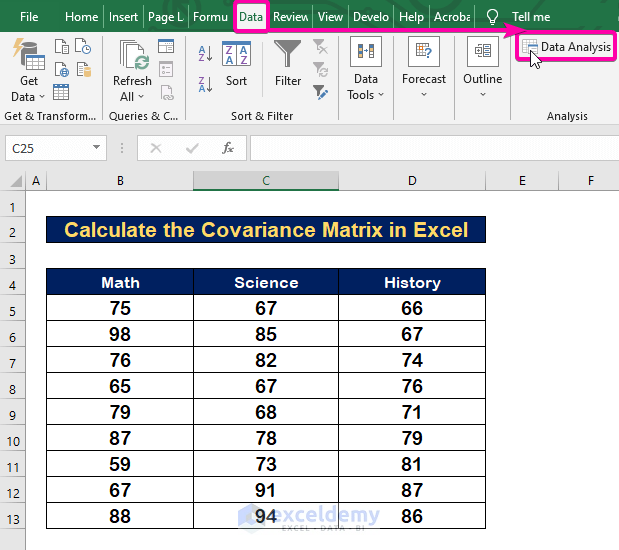
Step 1: Apply Data Analysis Command in Excel
- Click on the Data tab.
- From the Analysis group, select the Data Analysis command.
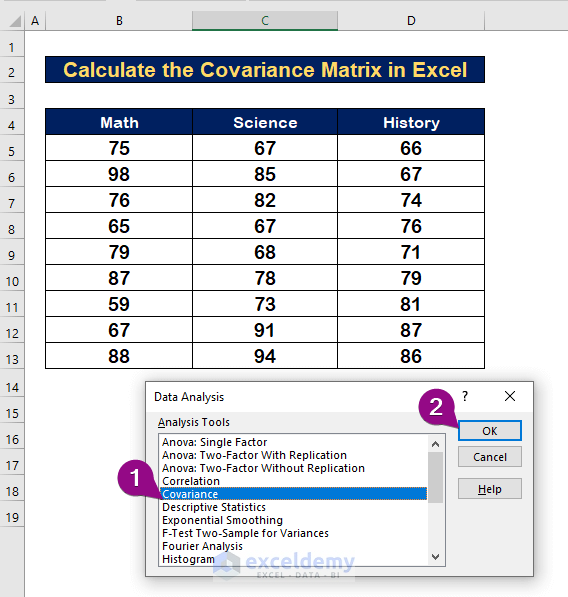
Step 2: Select Covariance Option from Analysis Tool
- From the Analysis Tools list, select the Covariance option.
- Then, click OK.
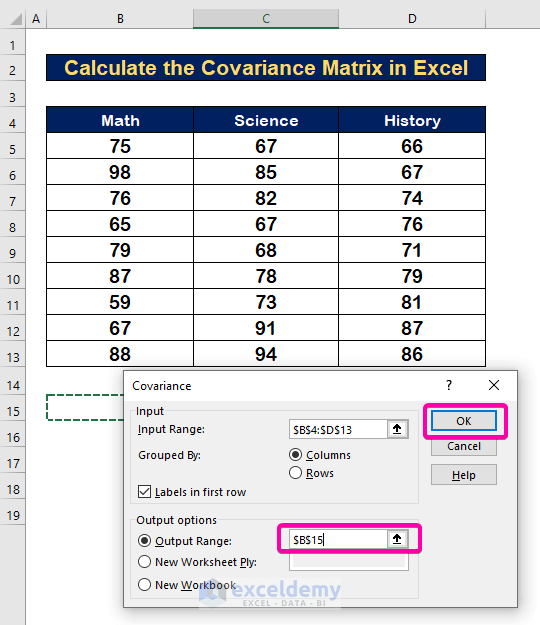
Step 3: Select Range to Calculate Covariance Matrix in Excel
- To calculate variance with Math, Science, and History, select the Input Range B4:D13 with the Header.
- Select the Labels in first row box.
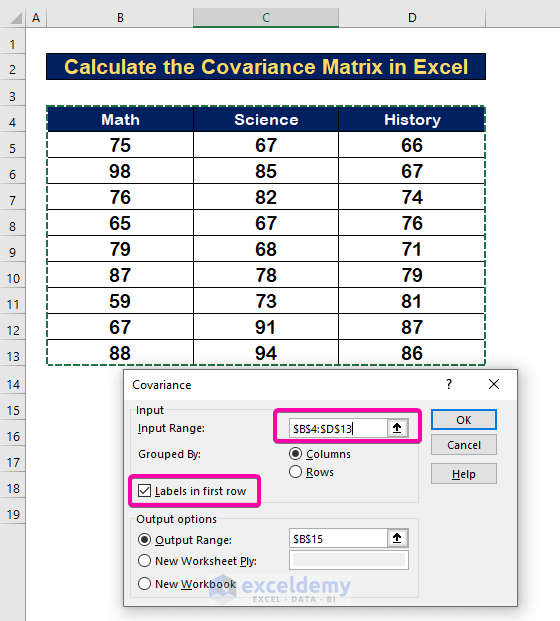
- For Output Range, select any cell (B15).
- Finally, click OK.
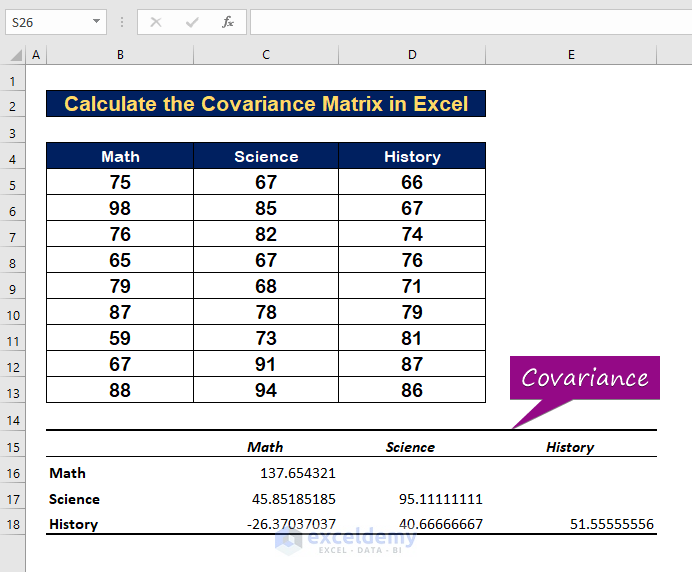
- As a result, the covariances will appear as in the image shown below.
Similar Readings
- How to Multiply 3 Matrices in Excel
- Create Traceability Matrix in Excel
- How to Create a Risk Matrix in Excel
- Make an Eisenhower Matrix Template in Excel
How to Interpret Covariance Matrix in Excel
You can interpret the relationships between single and multiple variables once you’ve created the covariance matrix.
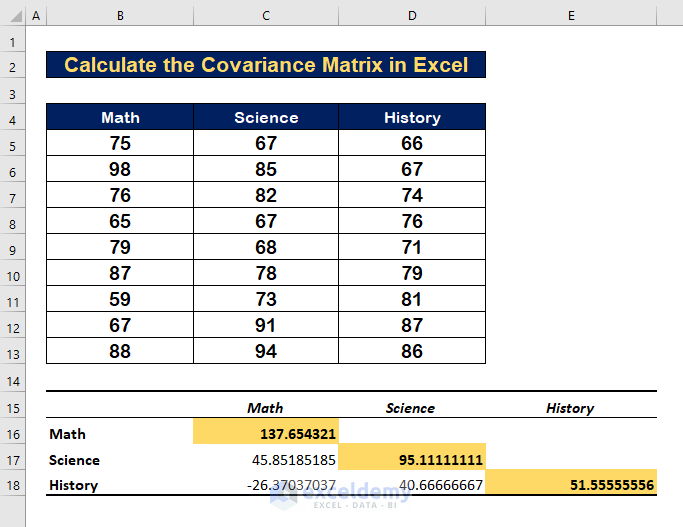
1. Covariance for a Single Variable
In the following image, we have highlighted the variances for each subject:
- The variance of Math with its mean is 137.654321.
- The variance of Science is 95.1111.
- Finally, the variance of History is 51.5555.
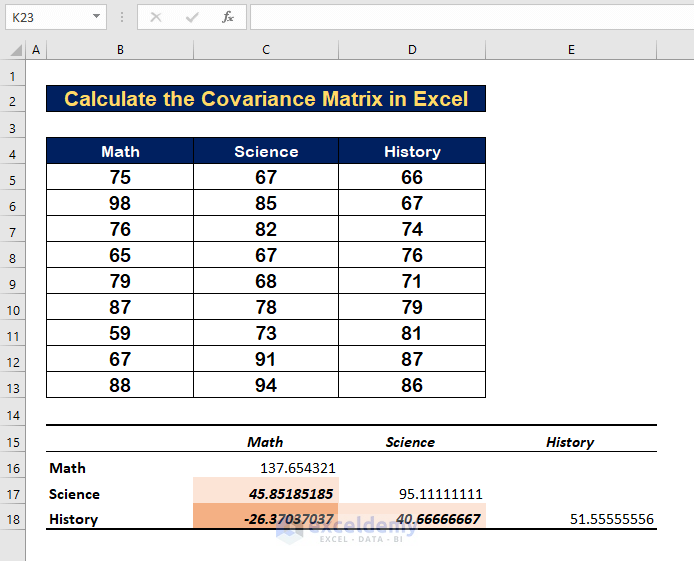
2. Covariance for Multiple Variables
We have highlighted the following image with the values of the variances between two variables.
- The variance value between Math and Science is 45.85185.
- The variance value between Math and History is -27.3703.
- And, the variance value between Science and History is 86.66667.
Positive Covariance
The presence of positive covariance indicates that the two variables are proportionate. When one variable rises, the other tends to rise with it. As in our example, the covariance between Math and Science is positive (45.85185), implying that students who perform well in Math also perform well in Science.
Negative Covariance
Negative covariance, in contrast to positive covariance, means that when one variable wants to increase, the other wants to decrease. The covariance between Math and History in our example covariance is negative (-27.3703), indicating that students who score higher in Math will score lower in History.
 Notes:Â
If you cannot find the Data Analysis tool in your Data tab, you may need to activate the Data Analysis ToolPak first. To do so, follow the instructions below.
Steps:
- Firstly, go to Home.
- Then, click on Options.
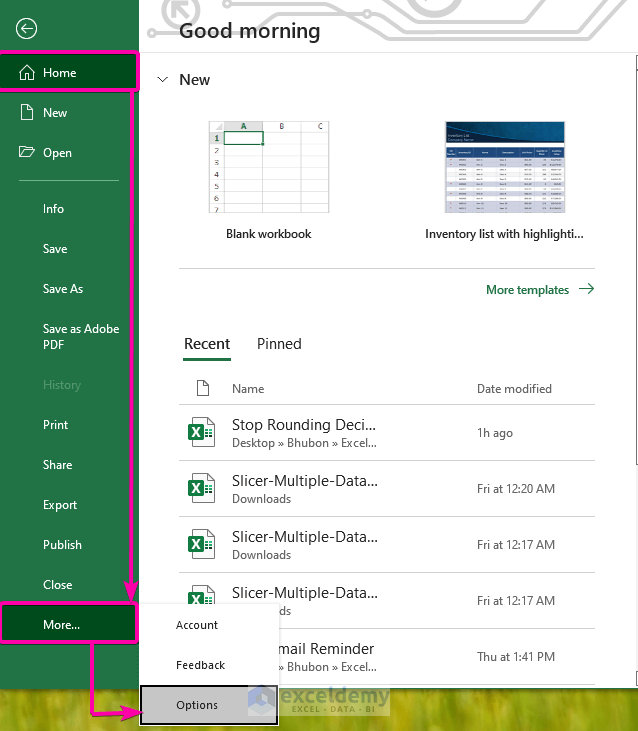
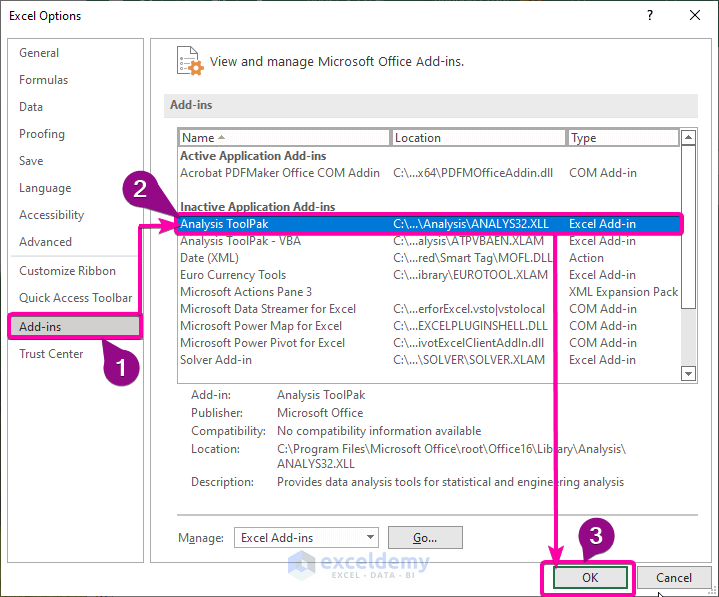
- From the Excel Options, select the Add-ins options.
- Then, click the Analysis ToolPak option.
- Finally, click OK.
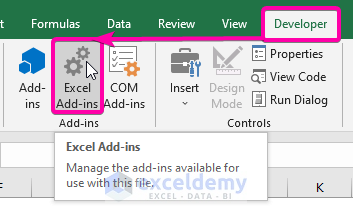
- Go to Developer tab.
- After that, from the Add-ins, click on Excel Add-ins command.
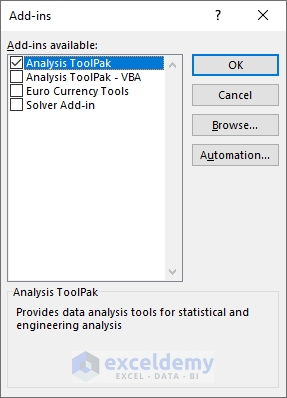
- Select the Analysis ToolPak from the list.
- Then, click OK to add the Add-ins.
- Consequently, you will find the Data Analysis command in your Data tab.
Download Practice Workbook
Download this practice workbook to exercise while you are reading this article.
Conclusion
I hope this article has given you a tutorial about how to calculate the covariance matrix in Excel. All of these procedures should be learned and applied to your dataset. Take a look at the practice workbook and put these skills to the test. We’re motivated to keep making tutorials like this because of your valuable support.
Please contact us if you have any questions. Also, feel free to leave comments in the section below.
Stay with us and keep learning.
