This tutorial will demonstrate how to use an Excel solver to rate sports team. Ratings are numerical representations of competitive strength which is directly comparable. It is often applied directly to predict the game outcome between any two teams. The Sports rating systems have been around for almost 80 years and use a variety of methods for rating teams. Today, we would like to discuss how to rate sports teams using Excel Solver.
What Is an Excel Solver?
Excel Solver is used in many different algorithms for finding the solution to different complex linear and non-linear problems. The methods of Excel solver are.
- GRG Nonlinear: The full form of this method is the Generalized Reduced Gradient Nonlinear method. Mainly for simple nonlinear problems where the data will contain a minimum of one constraint, this method is used.
- LP Simplex: We use Excel Solver for Linear Programming problems when linear relationships occur. With the linear connection with the data, linear programming tends to achieve the desired goal such as minimum loss, maximum profit, etc.
- Evolutionary: Among all the types, this is the most difficult where you can not determine the characteristics of the function. The system of this kind of function can increase or decrease at any time. This is because the functions are either discontinuous or nonsmooth.
How to Use Excel Solver to Rate Sports Team: with Easy Steps
If you follow the steps correctly, you should learn how to Excel Solver to rate sports teams on your own. The steps are:
Step 1: Arranging Dataset
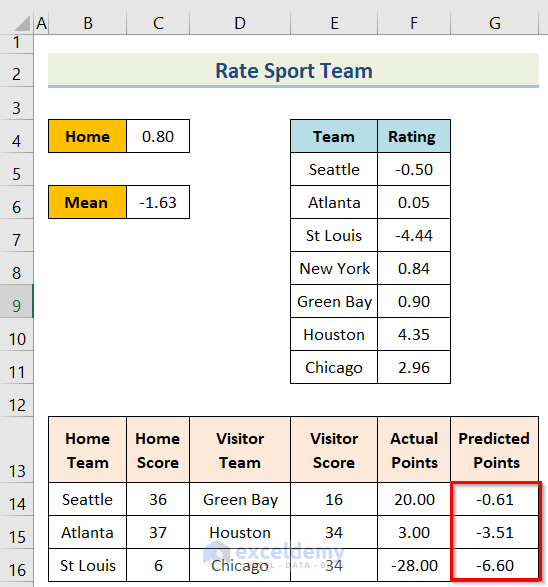
Our goal is to use the solver to rate sports teams in Excel. In this case, we have the Home in cell B4, Mean in cell B6, Team in cell E4, Rating in cell F4, Home Team, Home Score, Visitor Team, and Visitor Score sequentially in column B, column C, column D, and column E . We’ll use this sample dataset overview as an example in Excel to understand easily.
Step 2: Determining Predicted Points
Now, we want to determine the predicted points of the teams. To do so, we have to follow the below steps.
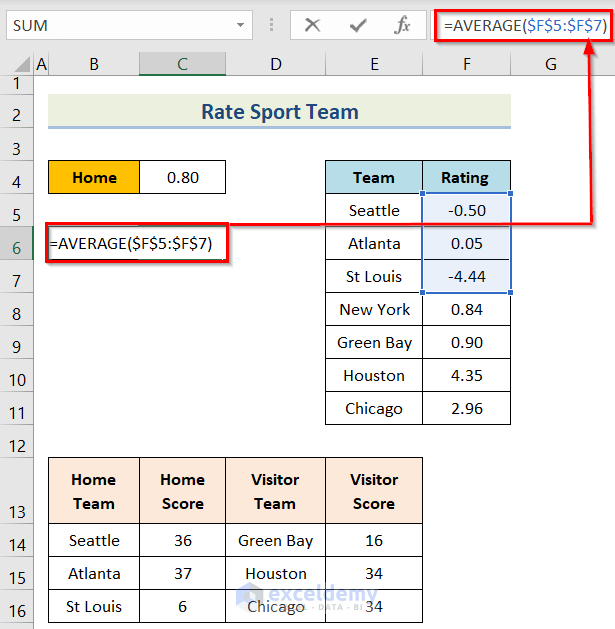
- First, insert the following formula in cell C6.
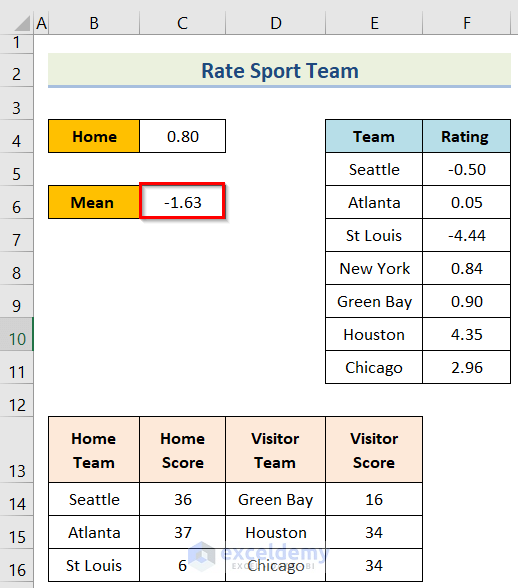
=AVERAGE($F$5:$F$7)- Second, you will get the desired result after pressing the Enter option.
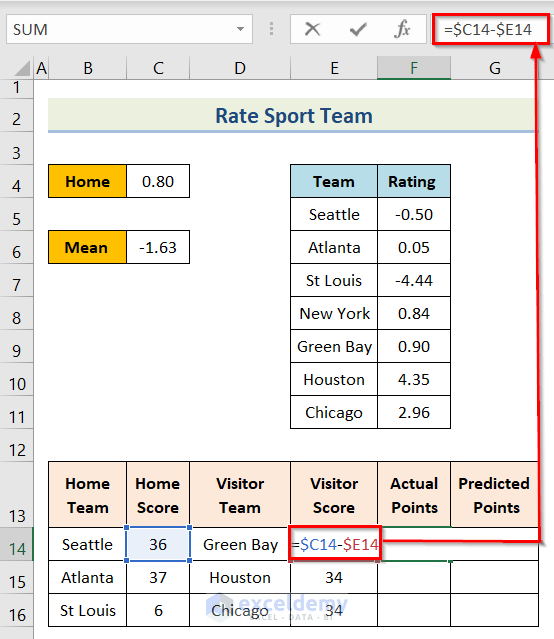
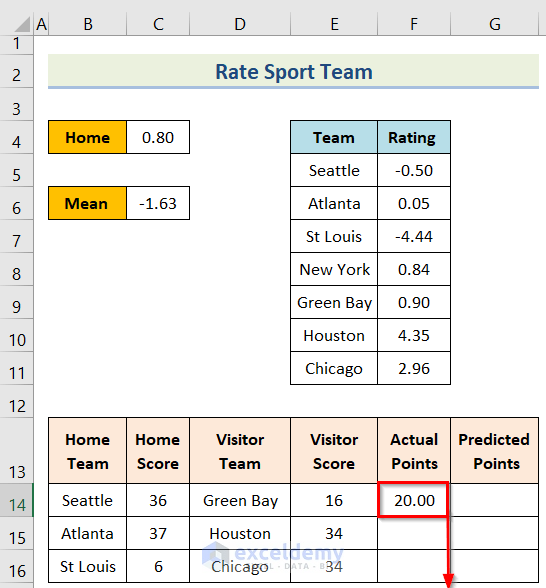
- Third, insert the following formula in cell F14.
=$C14-$E14- Fourth, you will get the result for the cell and then use the Fill Handle option.
- Fifth, you will get the desired result.
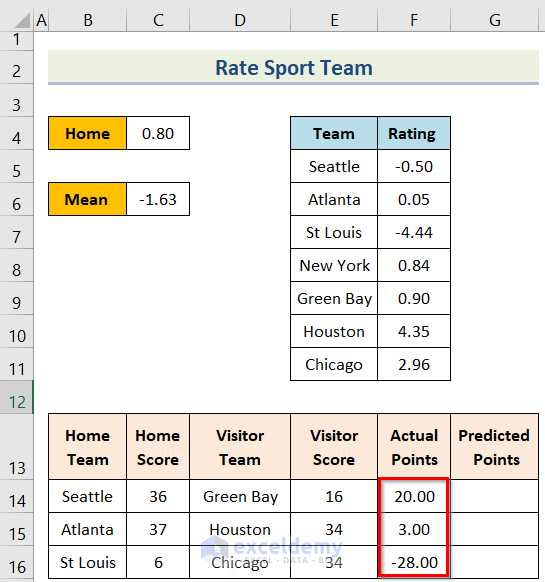
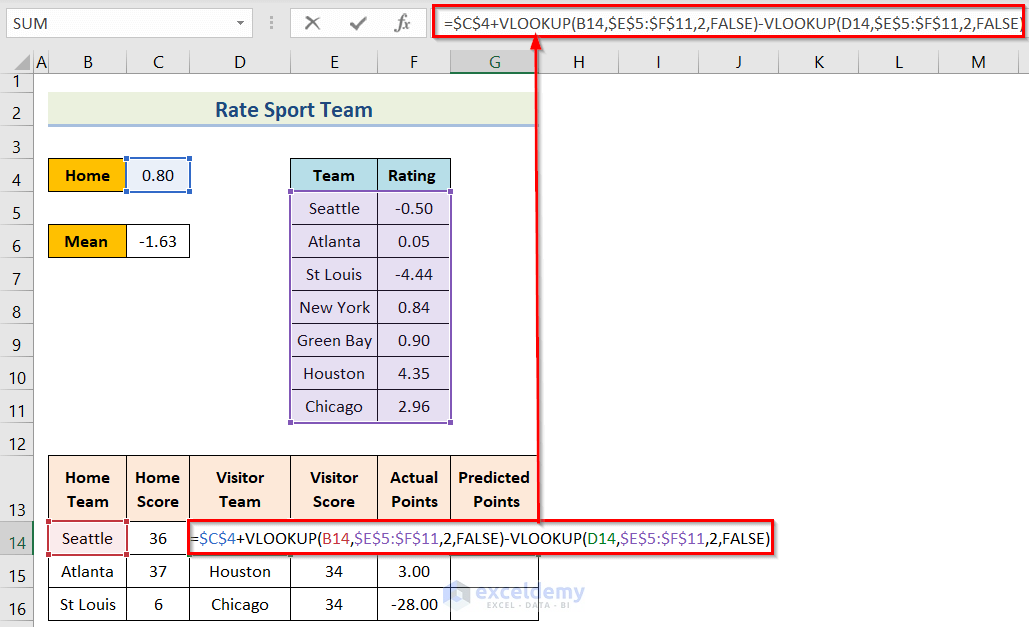
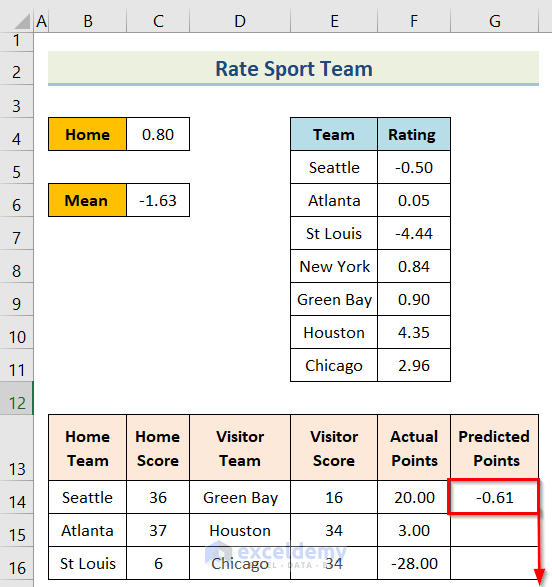
- Sixth, insert the following formula in cell G14.
=$C$4+VLOOKUP(B14,$E$5:$F$11,2,FALSE)-VLOOKUP(D14,$E$5:$F$11,2,FALSE)- Seventh, you will get the result for the cell and then use the Fill Handle option.
- Last, you will get the desired result.
Step 3: Calculating Square Error
To have an accurate result, we will also determine the square error. We can calculate square error by the following steps.
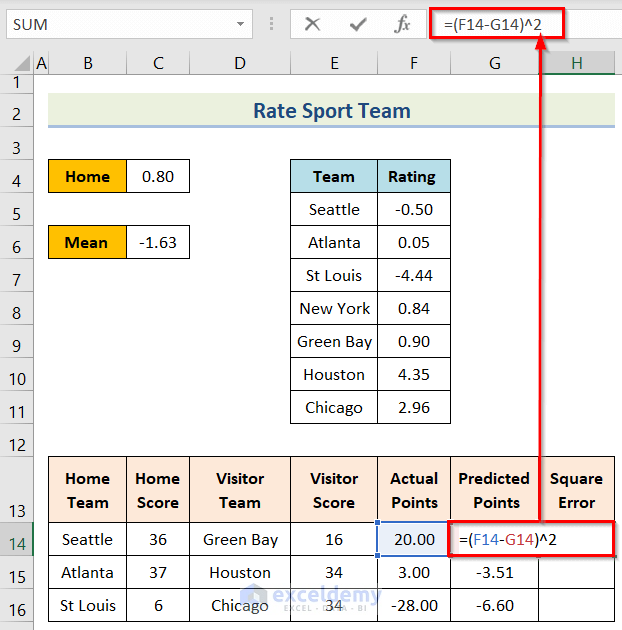
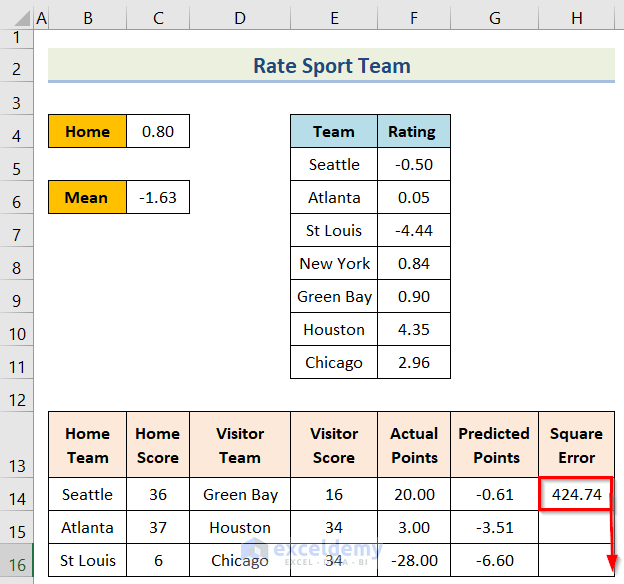
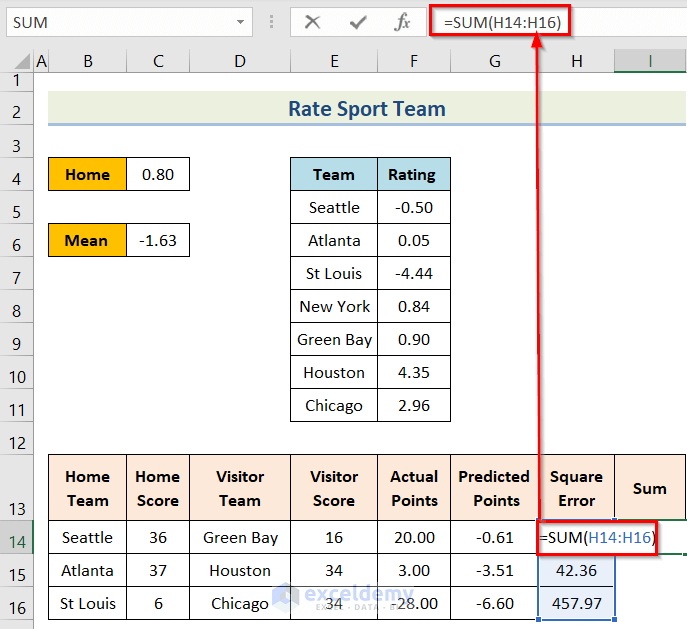
- To begin with, insert the following formula in cell H14.
=(F14-G14)^2- Furthermore, you will get the result for the cell and then use the Fill Handle option.
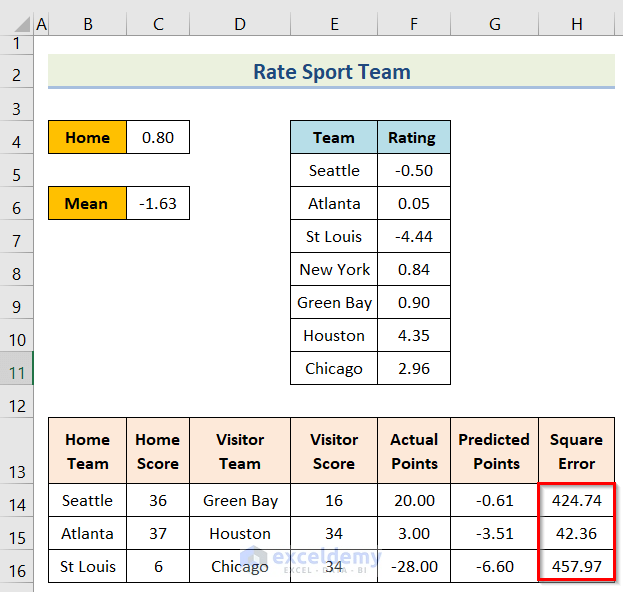
- Finally, you will get the desired result.
Read More: How to Do Portfolio Optimization Using Excel Solver
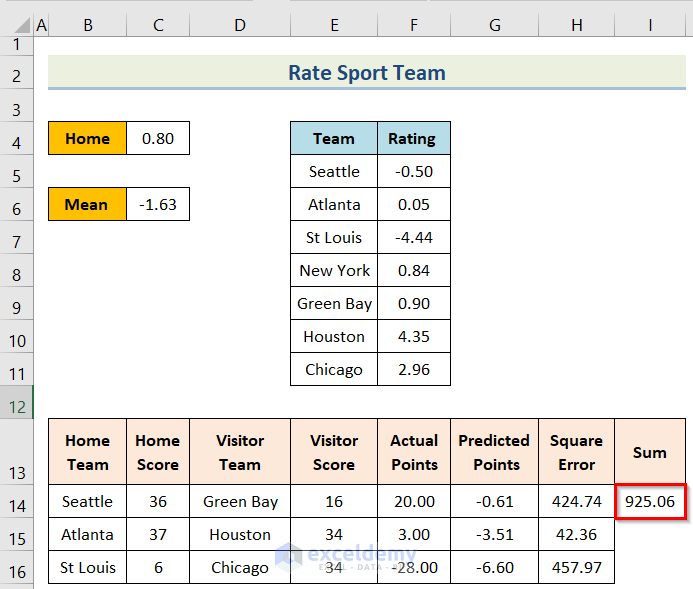
Step 4: Determination of Final Sum
In this case, we will determine the final sum of the process by following the below process.
- Firstly, insert the following formula in cell I14.
=SUM(H14:H16)- Lastly, you will get the desired result.
Read More: How to Use Excel Solver for Linear Programming
Step 5: Use of Excel Solver
If you already have a dataset of Points, Errors, and Sum but don’t have any team rating, then you can determine it using an Excel solver. Excel solver will give you a much more accurate value by predicting non-linear calculations. We will use an Excel solver to ease our work in the following steps.
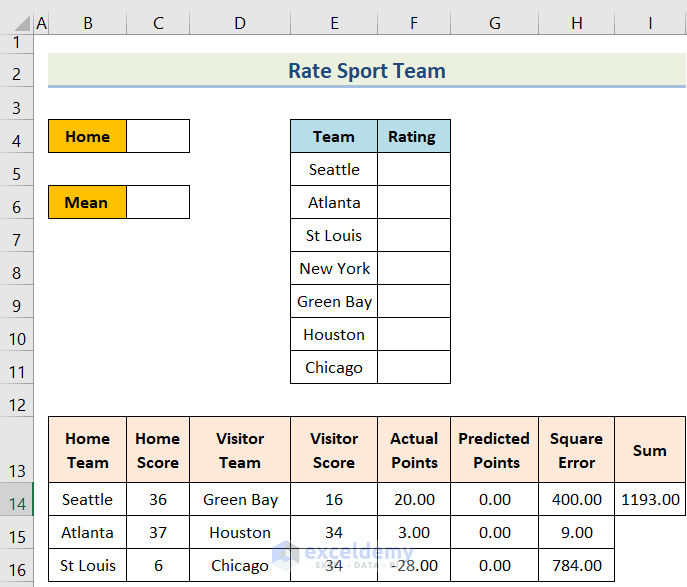
- First, we have arranged a dataset where the team rating is missing.
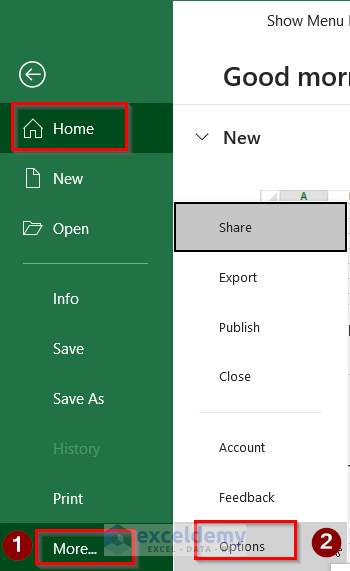
- Next, go to the File option.
- Then, go to More…>Options.
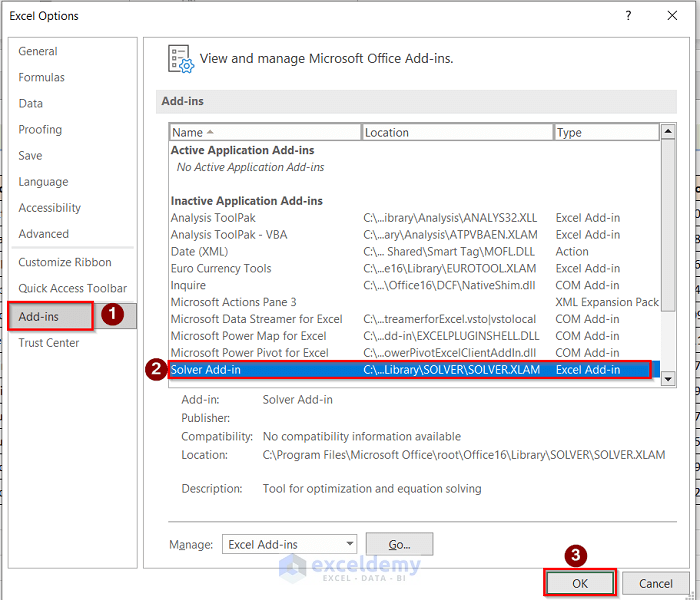
- Next, go to Add-ins > Solver Add-ins > OK options.
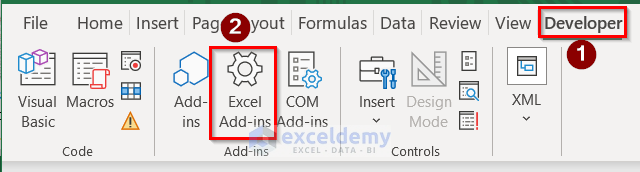
- After that, in the Developer tab, select the Excel Add-ins option.
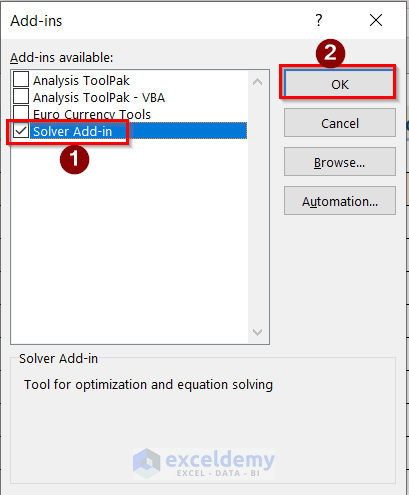
- Afterward, tick the Solver Add-in option and press OK.
- Furthermore, go to Data>Solver options to open the Solver Parameters dialog box.
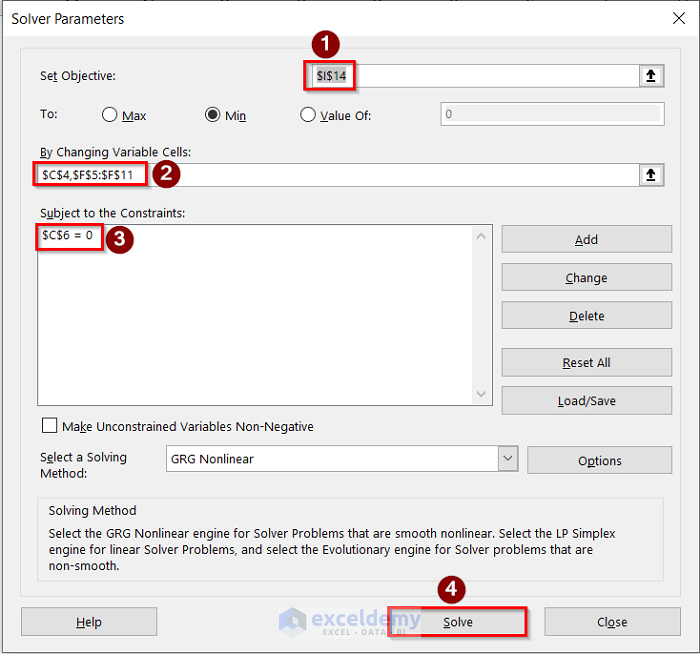
- The Solver Parameters dialog box for this model is shown below image. Select the desired target cell in the Set Objective Section, the constraints cell in the Subject to the Constraints section, and the cells that will be used to change are selected in the By Changing Variable Cells section.
- After clicking on the Solve and then OK in the Solver Results dialog box, we can get the following results.
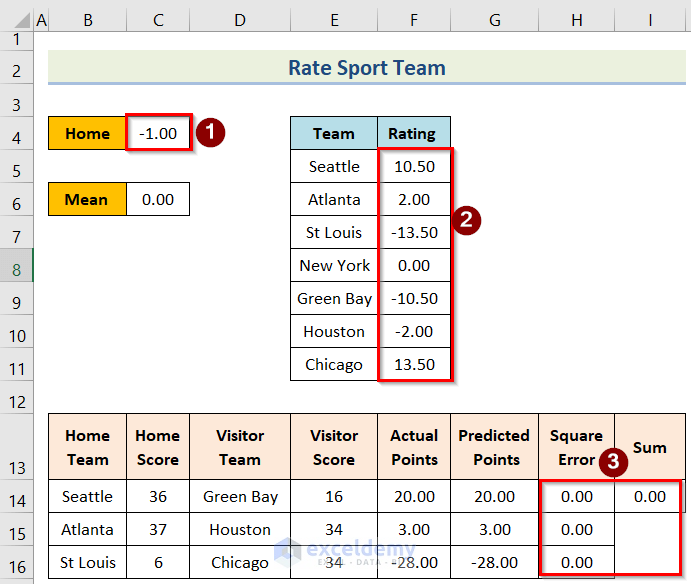
- Finally, you will get the desired result with the below changes.
Read More: Example with Excel Solver to Minimize Cost
Things to Remember
- From the problem, we can see that our objective is to give ratings for each team. Home-field edge and Team ratings are By Changing Cells in our problem instead of in our process.
- We want the prediction to be as close as possible to the outcome of each game. It implies that to minimize the sum overall differences between the Actual outcome and the Predicted outcome can be used as the target cell.
- However, there is a problem with this process. The positive and negative prediction errors can cancel each other out. For example, if you over-predict the home team margin by 5 points in one game and under-predict the home team margin by 5 points in another game, the sum of the two differences will yield a value of 0. But in fact, you were off by 10 points for a game. To not cancel out both positive and negative errors, we can use another method – to add up 2 powers of [(Actual Outcome) – (Predicted Outcome)] for all games.
- Another thing that requires your attention is that this model is no longer a simple LP model. We selected GRG Nonlinear engine in the last step.
Download Practice Workbook
You can download the practice workbook from here.
Conclusion
Henceforth, follow the above-described methods. Hopefully, these methods will help you to rate sports team in Excel Solver. We will be glad to know if you can execute the task in any other way. Please feel free to add comments, suggestions, or questions in the section below if you have any confusion or face any problems. We will try our best to solve the problem or work with your suggestions.
Related Articles
- How to Use Excel Solver to Determine Which Projects Should Be Undertaken?
- Solving Sequencing Problems Using Excel Solver Solution
- Solving Transportation or Distribution Problems Using Excel Solver
- How to Assign Work Using Evolutionary Solver in Excel
- Resource Allocation in Excel
- How to Create Financial Planning Calculator in Excel
- Solving Equations in Excel
<< Go Back to Excel Solver Examples | Solver in Excel | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!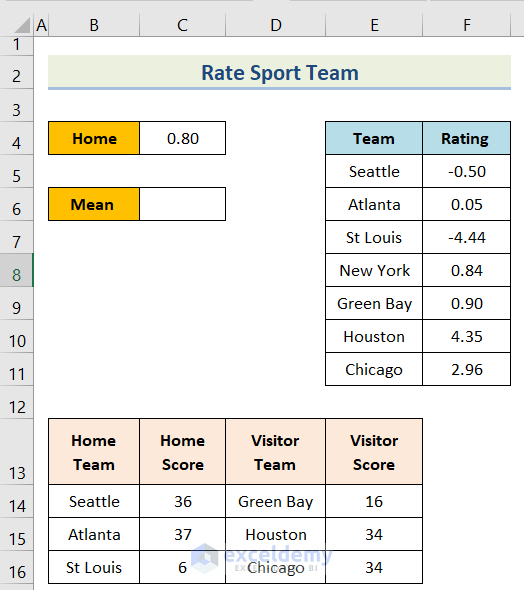



Just found this article on GR i am not sure in your explanation when you said seattle has 4 point better than st Louis. Can you please explsin this?
Thank you
Thanks for your question. Here Seattle has a rating of -0.50409…And St Louis Rams has -4.439784. if you subtract -0.50409 from the -4.439784, then you will get 4.943874.which is approximately around 4. So the statement that “Seattle has 4 points better than St Louis”
I think is much better to obtain the average points per game.
Home team vs Opponent team and then to obtain (MOV) Margin of Victory. MOV +/-
Thus this will give you a better point of view which team will win the match.
And or Apply forecast or trend functions at least with the last three seasons.
I know all we have a different way or sistem to predict game scores.
Thanks a lot for your comment, we will take your suggestions into consideration in the future.