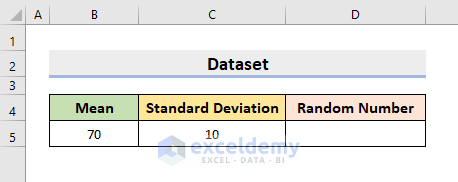
Dataset Overview
To illustrate, we’ll use a sample dataset as an example. For instance, the following dataset specifies the Mean and Standard Deviation.
Introduction to Normal Distribution
The Normal Distribution is also known as a Bell Curve. The theory is based on the idea that the distribution of values mainly clusters around an average. Still, very high and very low values are possible in certain cases. But they are rare compared to the ones closer to the average.
Method 1 – Using NORMINV Function
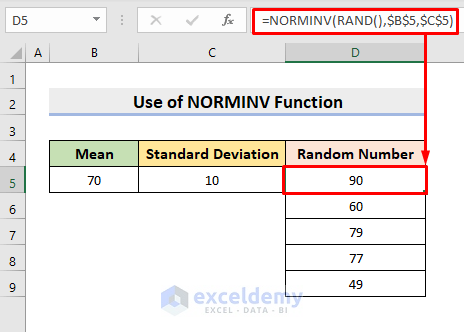
- The NORMINV function generates the inverse of the normal cumulative distribution.
- Specify the mean and standard deviation as arguments.
- Follow these steps:
- Select cell D5.
=NORMINV(RAND(),$B$5,$C$5)
- Press Enter.
- Use the AutoFill tool to generate 4 more numbers.
- Here, B5 represents the Mean, and C5 represents the Standard Deviation. The probability is input using the RAND function.
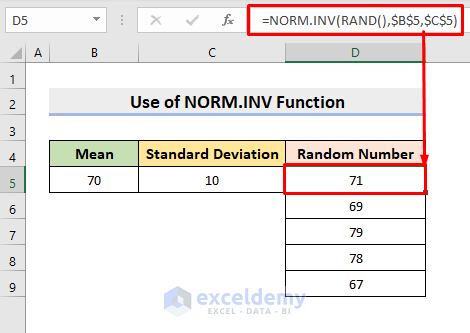
Method 2 – Excel’s NORM.INV Function
- This method is similar to Method 1, but more compatible with recent Excel versions.
- Steps:
- Select cell D5.
- Enter the formula:
=NORM.INV(RAND(),$B$5,$C$5)- Press Enter.
- Use AutoFill to fill the series.
B5 represents the Mean and C5 denotes the Standard Deviation. We utilize the RAND function to generate the necessary probability for this parameter.
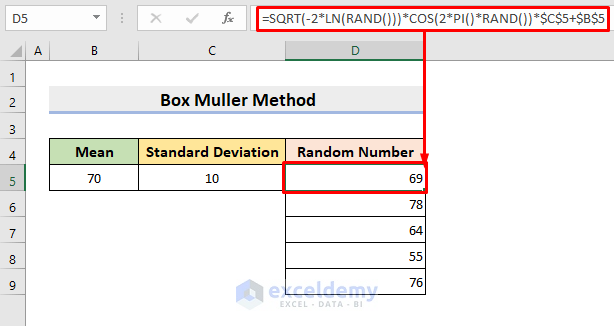
Method 3 – Box Muller Method
In this method, we’ll create a formula combining different Excel functions to apply the Box Muller method.
- Select cell D5. Enter the formula:
=SQRT(-2*LN(RAND()))*COS(2*PI()*RAND())*$C$5+$B$5- Press Enter and use AutoFill to fill the series.
How Does the Formula Work?
- RAND() – The RAND function generates random numbers.
- LN(RAND() – The LN function returns the natural logarithm of the numbers returned by the RAND function.
- COS(2*PI()*RAND() – The COS function returns the cosine of 2*PI()*RAND().
- SQRT(-2*LN(RAND()))*COS(2*PI()*RAND())*$C$5+$B$5 – The SQRT function returns random numbers.
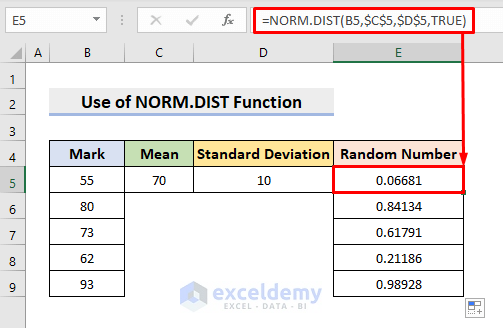
Method 4 – NORM.DIST Function
In our previous method, we’ll employ the NORM.DIST function to generate random numbers. This function yields values following a normal distribution, but it necessitates specifying the mean and the standard deviation. Therefore, acquaint yourself with the ensuing steps to generate random numbers.
STEPS:
- Select cell E5.
- Then, enter the formula:
=NORM.DIST(B5,$C$5,$D$5,TRUE)- Press Enter.
- Use AutoFill to return 4 more numbers.
Download Practice Workbook
You can download the practice workbook from here:
<< Go Back to Random Number in Excel | Randomize in Excel | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!