What Are Option Greeks?
Option Greeks are monetary indicators of how sensitive the price of an option is to the factors that determine it, such as volatility or the value of the underlying asset. There are 5 commonly used options for Greeks.
| Name | Dependent Variable | Independent Variable |
|---|---|---|
| Delta | Strike Value | Value of Underlying Asset |
| Gamma | Delta | Value of Underlying Asset |
| Vega | Strike Value | Volatility |
| Theta | Strike Value | Time of Maturity |
| Rho | Strike Value | Rate of Interest |
What Is Greek Delta?
Delta is a measurement of an option’s value changes in the value of the elemental asset. The formula for the DELTA function is:
N is the normal distribution of the share price, and the formula for d1 is
S= Price of Underlying Asset.
K= Strike Price.
σ= Volatility.
r= Risk-Free Factor Rate.
The function is typically calculated as a decimal between -1 and 1. Puts have a value of -1 to 0, while Call options can have a value of 0 to 1. The money value is deep-in-the-money the closer its delta is near 1 or -1.
Another name for Option Greek Delta is the hedge ratio.
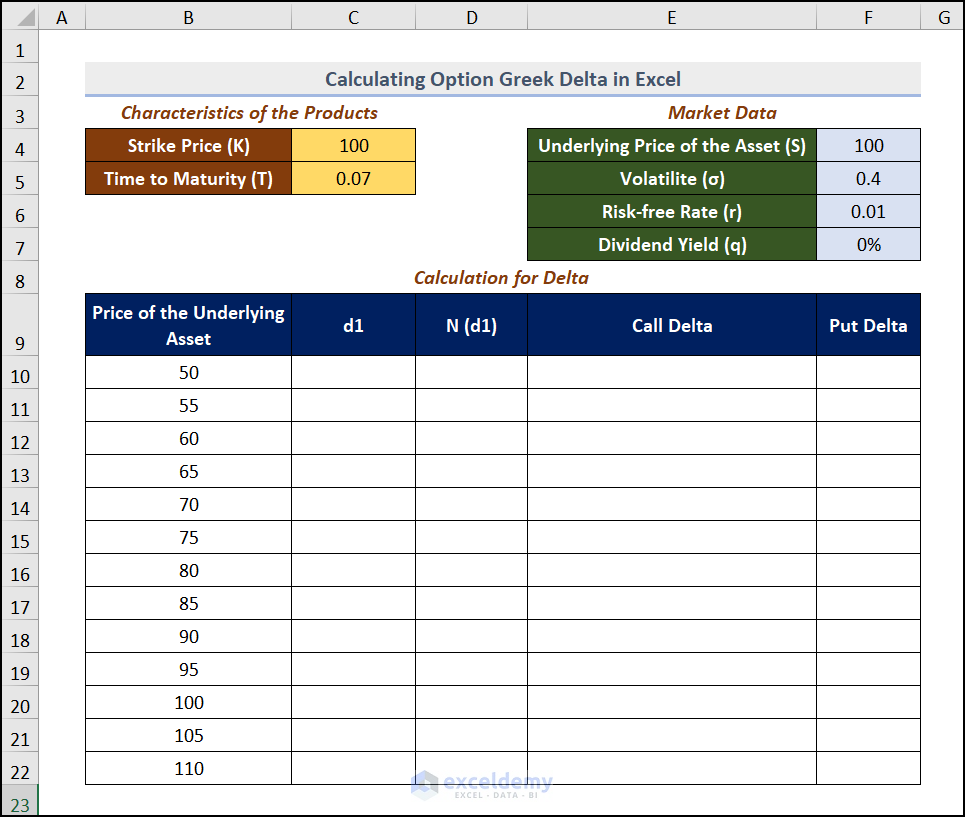
Step 1 – Inputting the Entities
- Enter all entities related to the calculation.
- Here, Strike Price (k), Time to Maturity (T), and Volatility. Risk-free factor, and Underlying Price of the Asset.
Read More: How to Calculate Delta in Excel
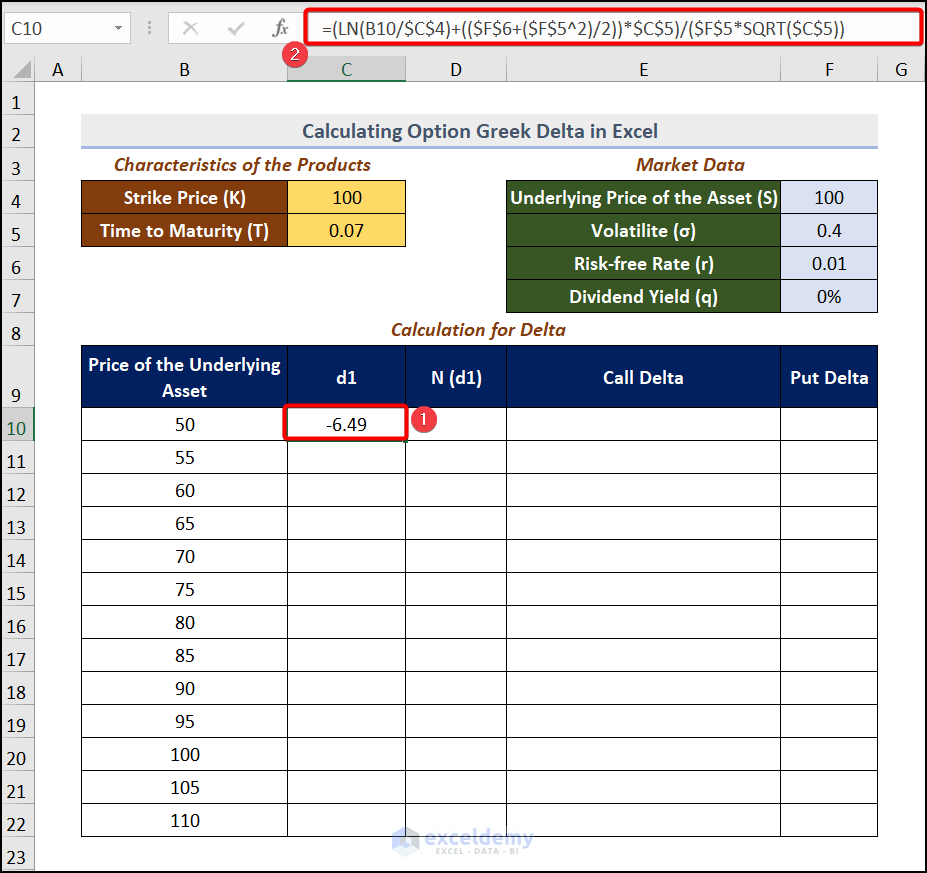
Step 2 – Calculate the Distribution
- Go to C10 and enter the formula.
=(LN(B10/$C$4)+(($F$6+($F$5^2)/2))*$C$5)/($F$5*SQRT($C$5))B10= Underlying Price of the Asset.
$C$4= Strike Price (k)
$C$5= Time to Maturity (T)
$F$5= Volatility ()
$F$6= Risk-free Rate ®
The LN function calculates the logarithmic value, and the SQRT function returns the square root value of C5.
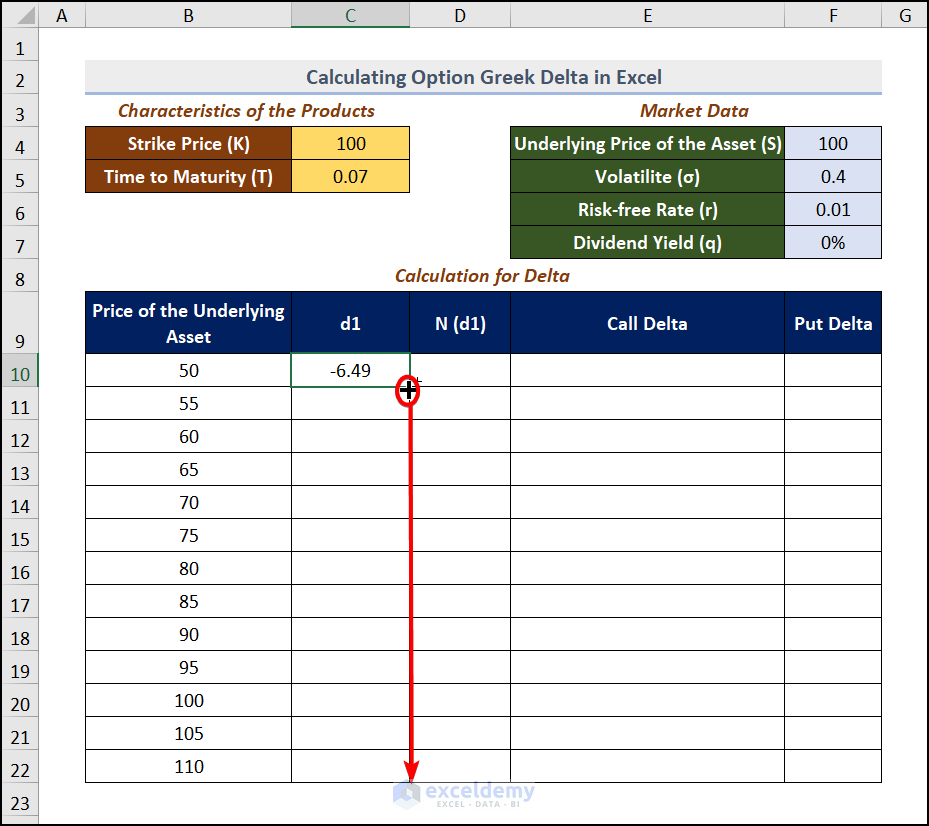
- Press ENTER and drag down the Fill Handle.
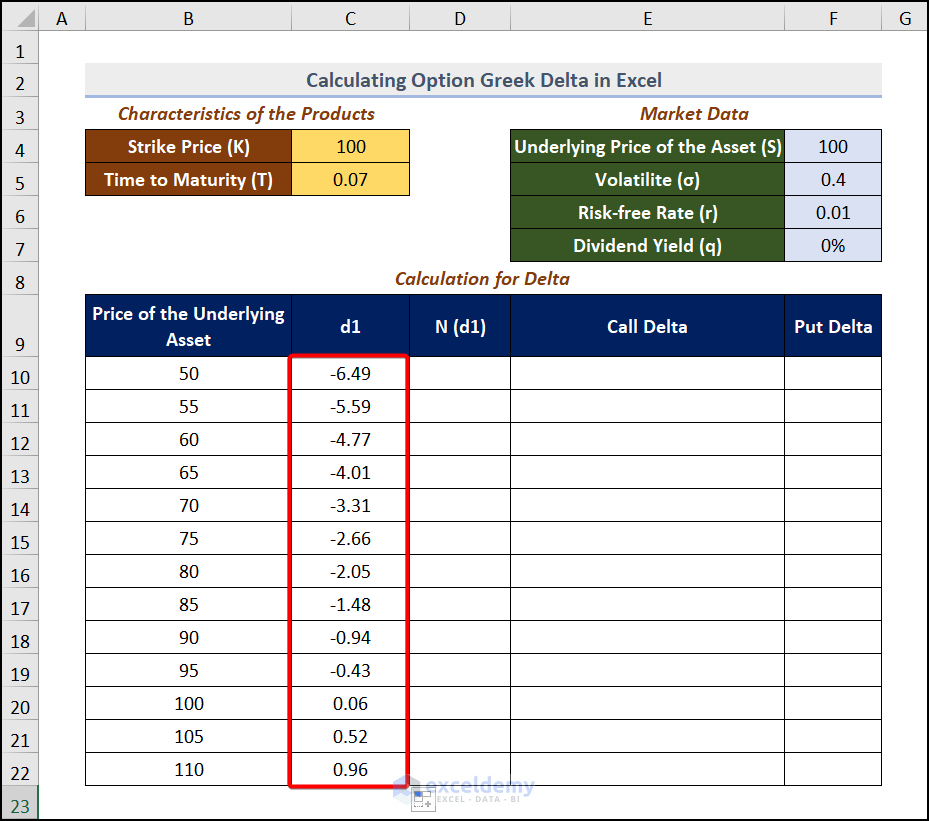
The distribution value will be displayed.
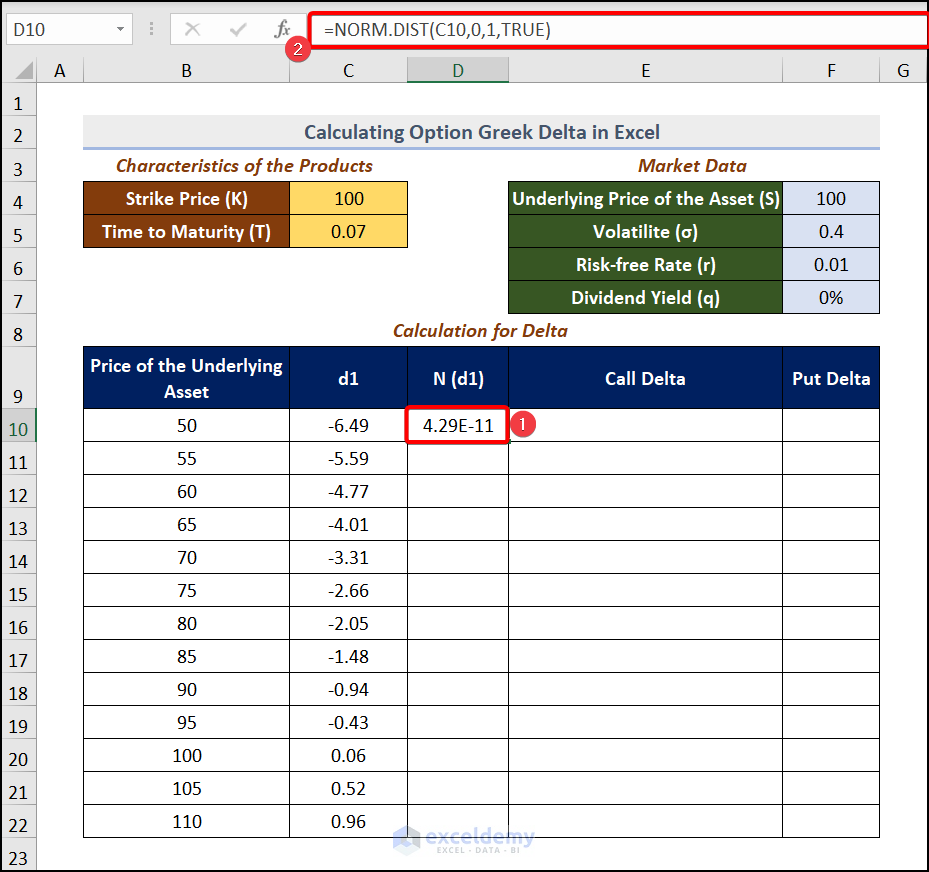
- Go to D10 and enter the formula.
=NORM.DIST(C10,0,1,TRUE)The NORM.DIST function returns the normal distribution for Mean and Standard deviation.The NORM.DIST(C10,0,1, TRUE) syntax returns the normal distribution of C10 where 0 is the mean and 1 is the standard deviation. Here, TRUE stands for cumulative.
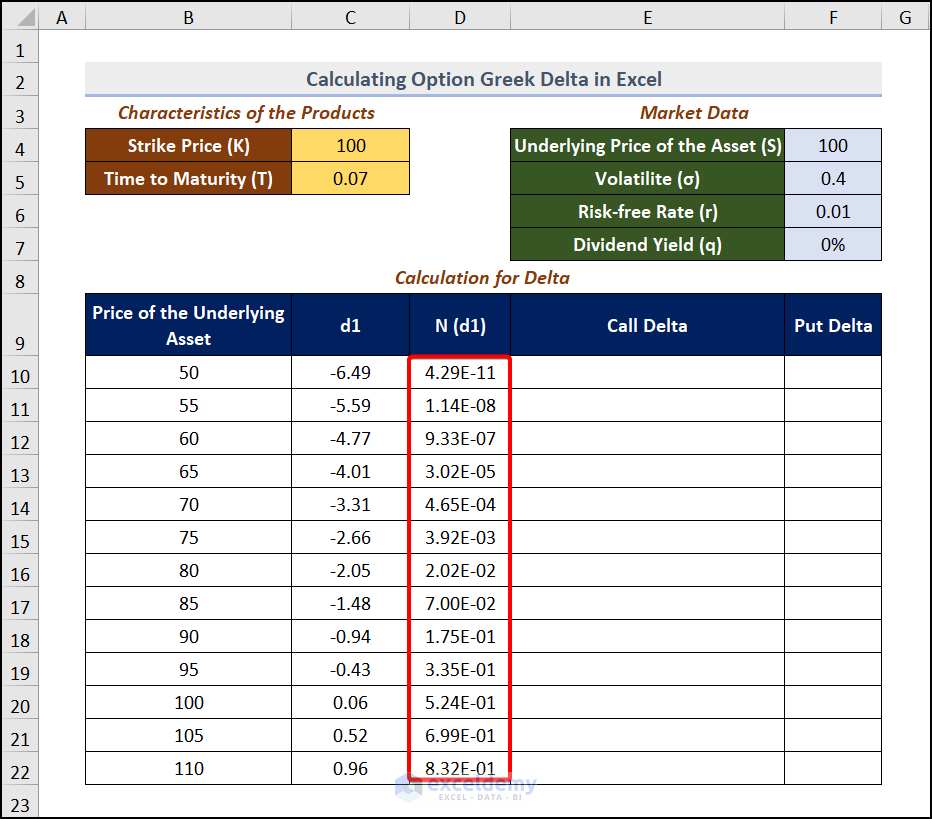
Get the N (d1) value after dragging down the Fill Handle.
Step 3 – Evaluate the Call Option
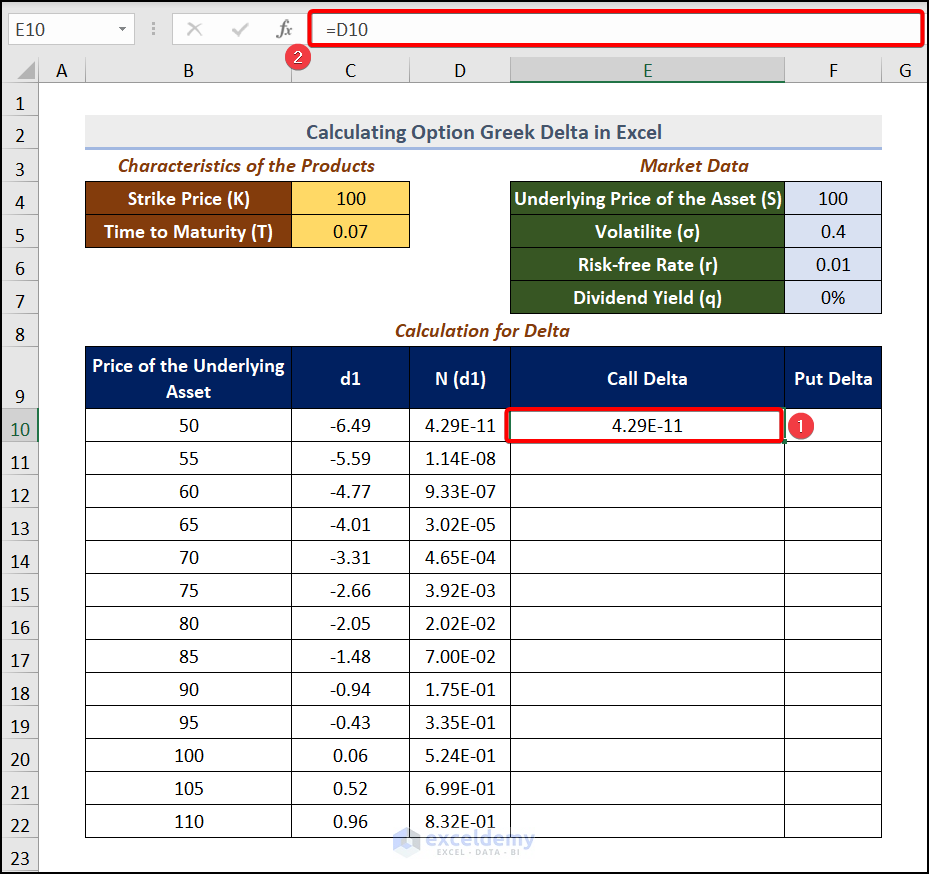
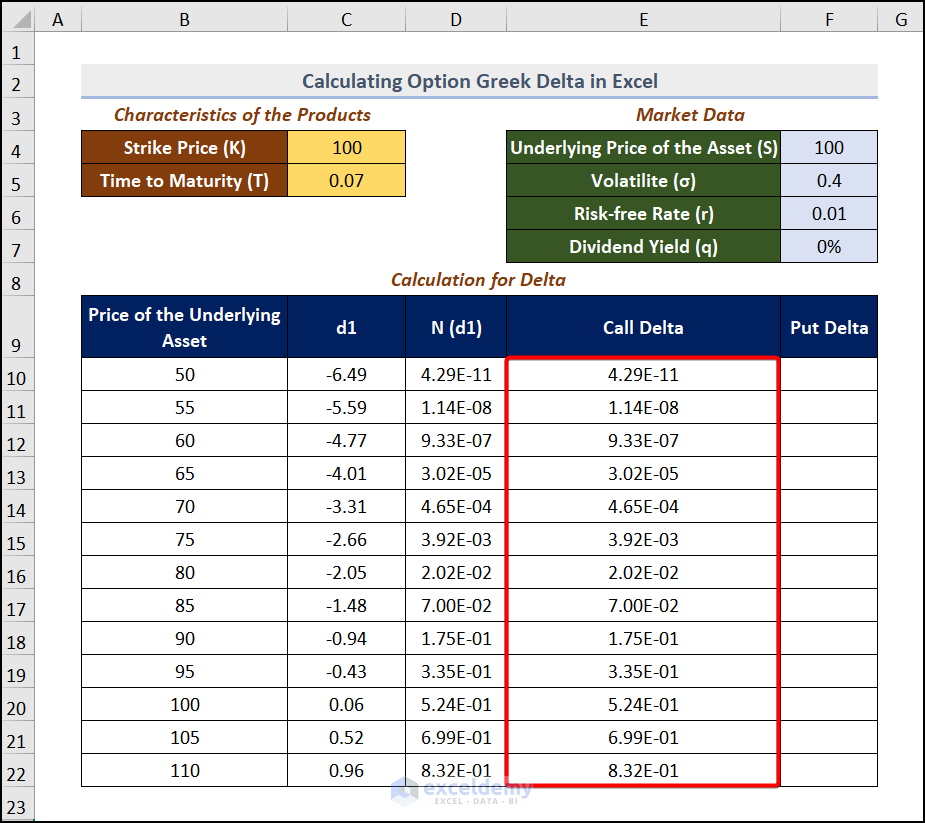
The Call options are evaluated as Call Delta= N(d1). N(d1) was calculated in D10:D22.
- To enter the value in E10:E22, enter the following in E10:
=D10
- Press ENTER and drag down the Fill Handle.
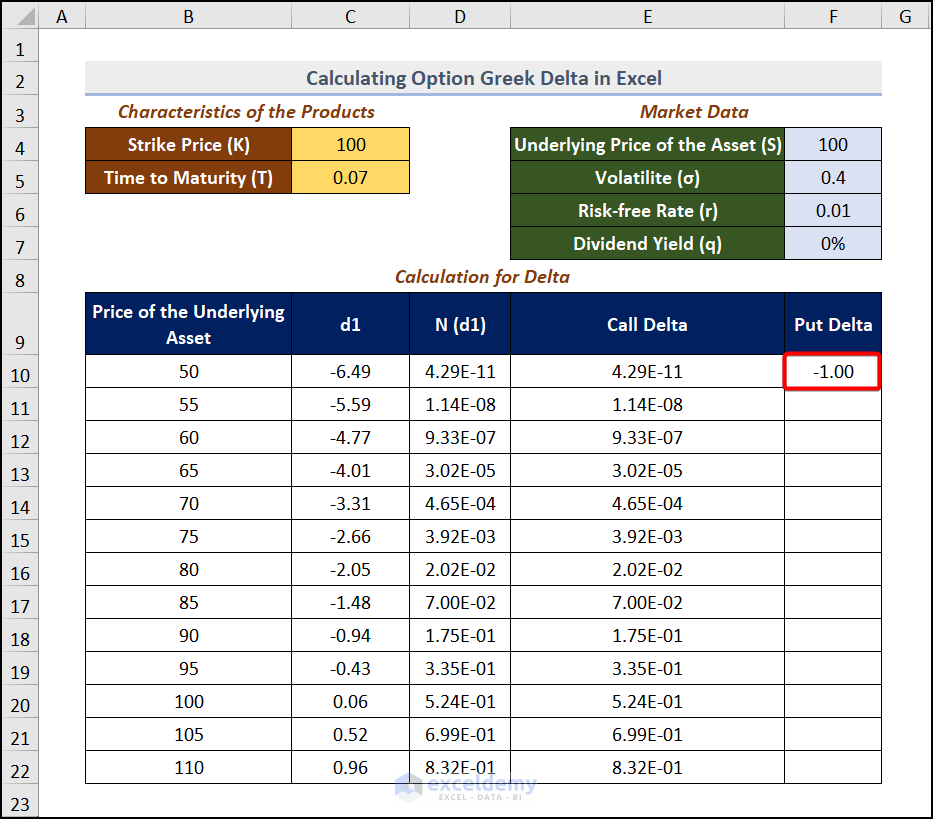
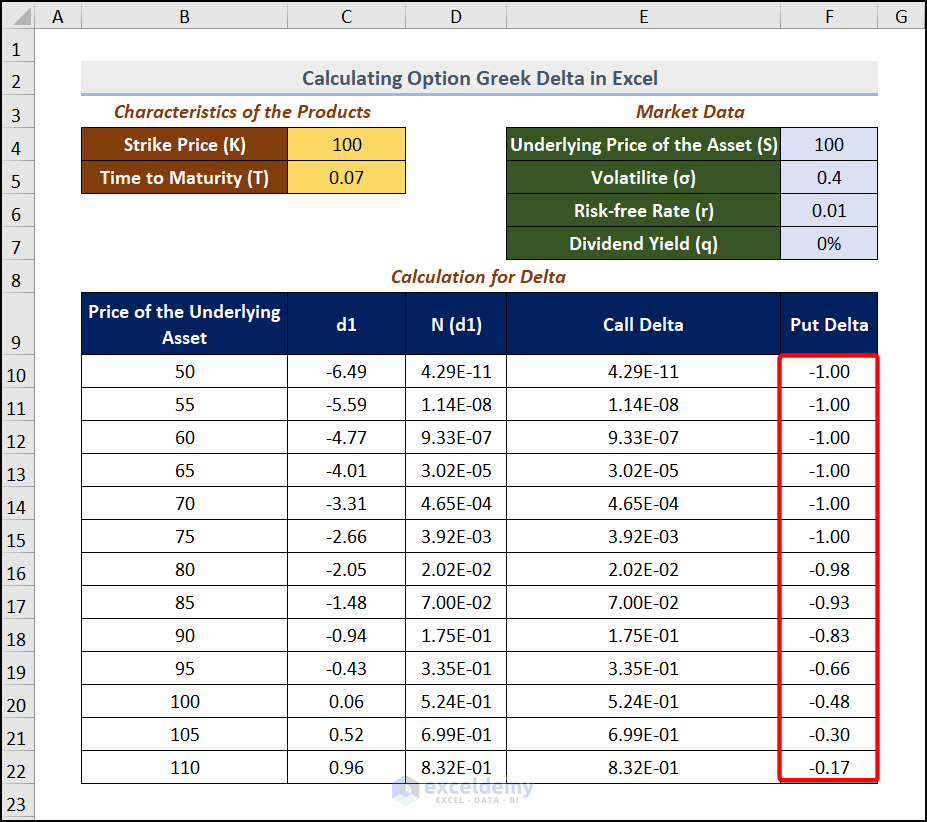
Step 4 – Estimate the Put Option
The formula for the Put option is =N(d1)-1.
- Go to F10 and use the formula
=E10-11 is subtracted from E10.
- Press ENTER and drag down the Fill Handle.
This is the output.
Practice Section
Practice here.
Download Practice Workbook
Download the practice workbook.
Related Articles
- How to Calculate Delta Percentage in Excel
- How to Calculate Delta E Color in Excel
- How to Calculate Delta Delta CT in Excel
- Delta Neutral Strategy in Excel
- Delta Hedging Example in Excel
- How to Calculate VaR Using Delta-Normal Method in Excel
<< Go Back to Excel DELTA Function | Excel Functions | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!
Nice article. How did you calculate the Time to Maturity? That is, what does 0.07 represent versus using the actual number of days to expiration?
Hello Wesley,
Thank you! Great question. The value 0.07 for Time to Maturity represents the fraction of a year until the option expires. It’s calculated by dividing the number of days to expiration by 365. For example, if the option expires in 25 days, Time to Maturity would be 25/365 ≈ 0.07. This approach standardizes the time input for the Black-Scholes model.
Regards
ExcelDemy