Whenever working with a set of data a regression line helps you to see the connection between the scatter data points. If you are looking for a way to find the Slope of a regression line then you have come to the right place. The focus of this article is to explain how to find the Slope of a regression line in Excel.
What Is Slope of a Regression Line?
A regression line generally shows the connection between some scatter data points from a dataset. The equation for a regression line is,
y = mx + b
Where,
- m = Slope of the Regression Line.
- B = Y-Intercept.
You can also use the following formula to find the Slope of a regression line.
m = ∑(x-µx)*(y-µy)/∑(x-µx)²
Where,
- µx= Mean of known x values.
- µy= Mean of known y values.
How to Find the Slope of a Regression Line in Excel: 3 Easy Ways
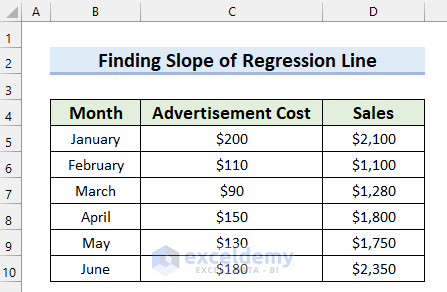
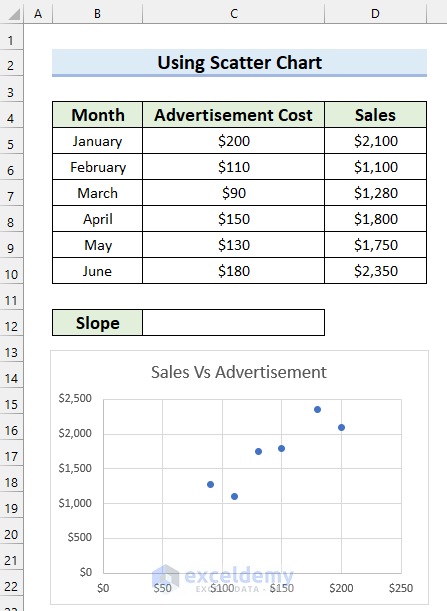
To explain this article, I have taken the following dataset. It contains 3 columns, the Month, Advertisement Cost, and Sales. I will use this dataset to explain how to find the Slope of a regression line in Excel in 3 different ways.
1. Use Excel Chart to Find the Slope of a Regression Line
In this first method, I will use an Excel chart to find the Slope of a regression line in Excel. Here, I will insert a Scatter Chart for the dataset and then find slope from it. Let’s explore the steps.
Step-01: Insert Scatter Chart in Excel
In this first step, I will insert the Scatter Chart.
- Firstly, select the data range with which you want to make the chart.
- Secondly, go to the Insert tab from the Ribbon.
- Thirdly, select Insert Scatter or Bubble Chart.
- Consequently, a drop-down menu will appear.
- Select Scatter.
- After that, you will see that you have inserted a Scatter Chart for your selected data.
- Click on the marked portion to change the Chart Title.
- Finally, I have changed the Chart Title and this is how my chart looks.
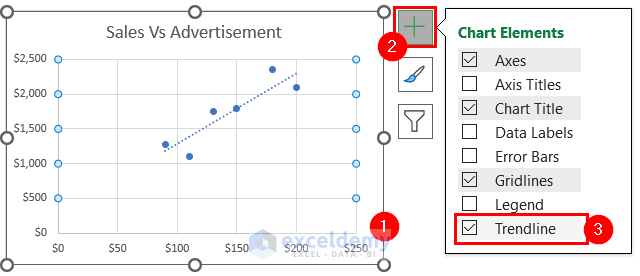
Step-02: Add Trendline
Now, I will add a Trendline to the Scatter Chart.
- In the beginning, select the chart.
- After that, select Chart Elements.
- Then, Check the Trendline option.
- After adding the Trendline this is how my chart looks.
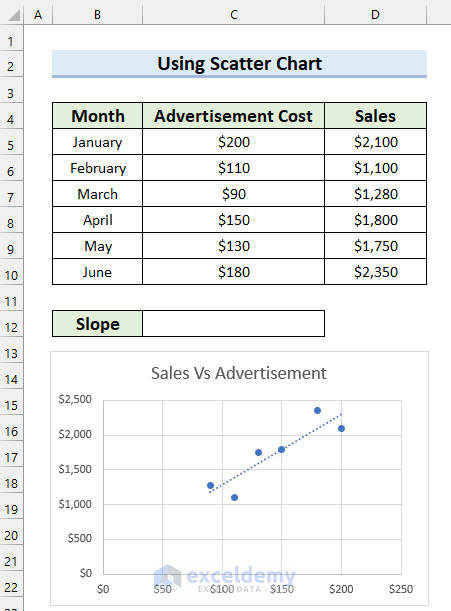
Step-03: Display Trendline Equation on Chart and Find Slope
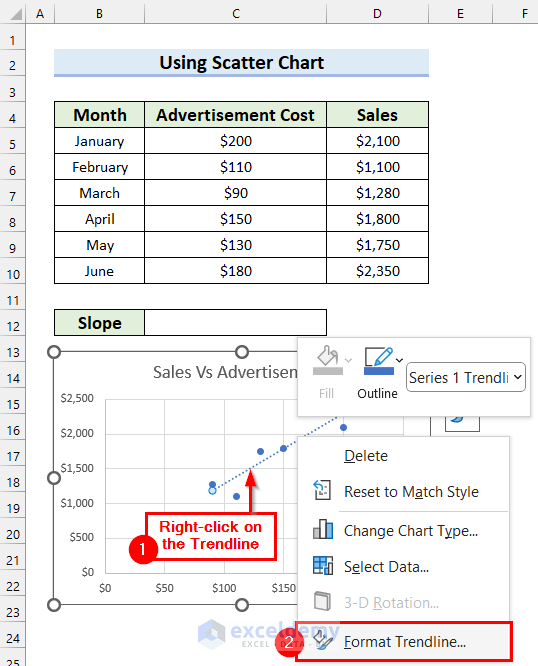
Here, I will display the Trendline Equation on the chart.
- To do that, Right-click on the Trendline.
- Then, select Format Trendline.
- Consequently, the Format Trendline task pane will appear on the right side of the screen.
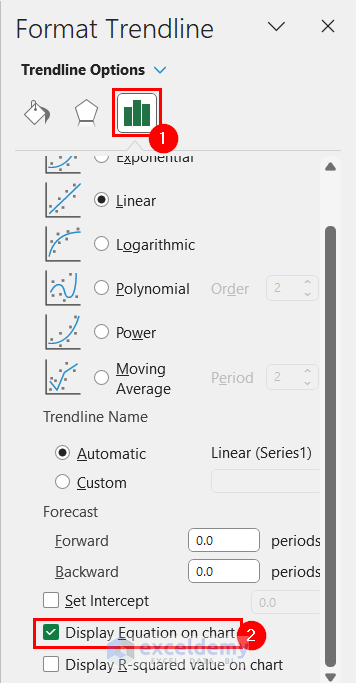
- Select the Trendline Options tab.
- After that, Check the Display Equation on chart option.
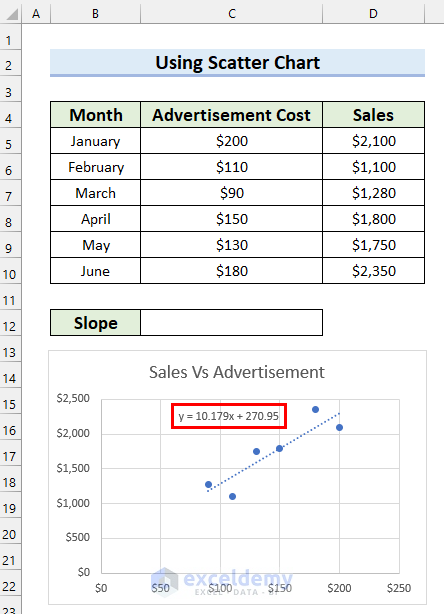
- After that, you will be able to see the equation for the Trendline on the chart.
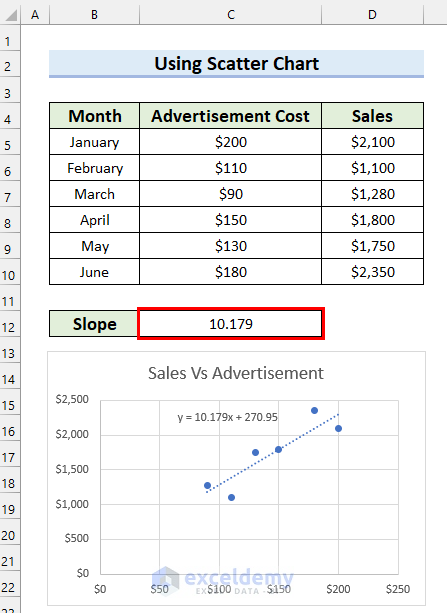
- Now, find out the Slope from the equation and write it down in your preferred location.
Read More: How to Find Instantaneous Slope on Excel
2. Apply SLOPE Function to Calculate the Slope of a Regression Line in Excel
You can also use the SLOPE function to find the Slope of a regression line in Excel. The SLOPE function returns the Slope of a regression line through known data points. Let’s see the steps of this calculation.
Steps:
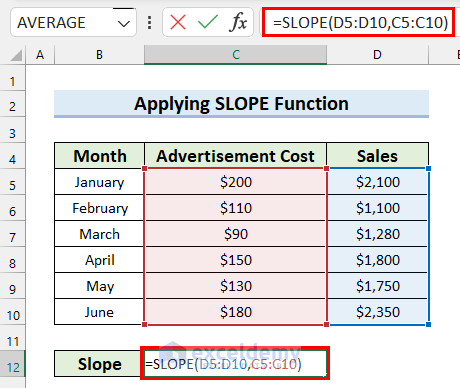
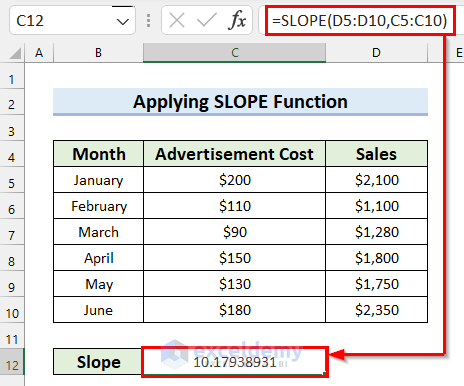
- Firstly, select the cell where you want the Slope. Here, I selected Cell C12.
- Secondly, in Cell C12 write the following formula.
=SLOPE(D5:D10,C5:C10)
- Thirdly, press Enter to get the result.
Here, in the SLOPE function, I selected cell range D5:D10 as known_ys, and C5:C10 as known_xs. The formula will return the slope of the regression line for these data points.
Read More: How to Find the Slope of a Line in Excel
3. Determine Slope of a Regression Line Manually Using SUM and AVERAGE Functions
Now, I will show you how you can determine the Slope of a regression line manually in Excel. I will use the SUM function and the AVERAGE function for this calculation. Let’s see the steps of this calculation.
Steps:
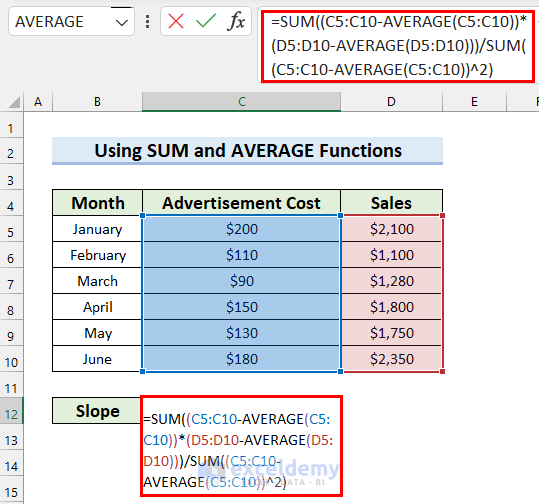
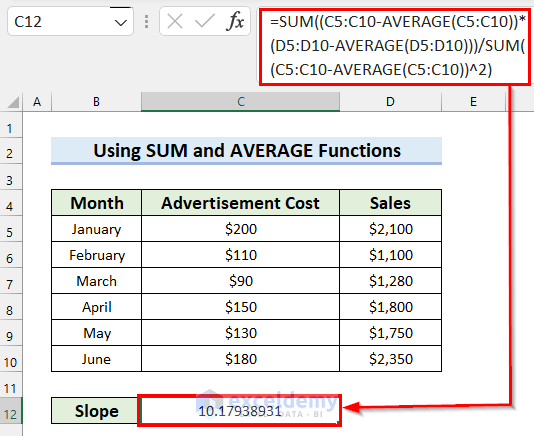
- In the beginning, select the cell where you want the Slope.
- Next, write the following formula in that selected cell.
=SUM((C5:C10-AVERAGE(C5:C10))*(D5:D10-AVERAGE(D5:D10)))/SUM((C5:C10-AVERAGE(C5:C10))^2)
- After that, press Enter to get the result.
🔎 How Does the Formula Work?
- AVERAGE(C5:C10): Here, the AVERAGE function returns the average of cell range C5:C10.
- (C5:C10-AVERAGE(C5:C10)): Now, the average is subtracted from the cell range C5:C10.
- AVERAGE(D5:D10): Here, the AVERAGE function returns the average of cell range D5:D10.
- (D5:D10-AVERAGE(D5:D10): Now, the average is subtracted from the cell range D5:D10.
- (C5:C10-AVERAGE(C5:C10))*(D5:D10-AVERAGE(D5:D10)): Here, the formula multiplies the results it got from the previous formulas.
- SUM((C5:C10-AVERAGE(C5:C10))*(D5:D10-AVERAGE(D5:D10))): Now, the SUM function returns the summation of these values.
- (C5:C10-AVERAGE(C5:C10))^2: Here, the average of cell range C5:C10 is subtracted from cell range C5:C10. And then raised to the power of 2.
- SUM((C5:C10-AVERAGE(C5:C10))^2): Now, the SUM function returns the summation of the values it got from the previous calculation.
- SUM((C5:C10-AVERAGE(C5:C10))*(D5:D10-AVERAGE(D5:D10)))/SUM((C5:C10-AVERAGE(C5:C10))^2): Finally, the first summation is divided by the second summation.
Read More: How to Find Slope of Logarithmic Graph in Excel
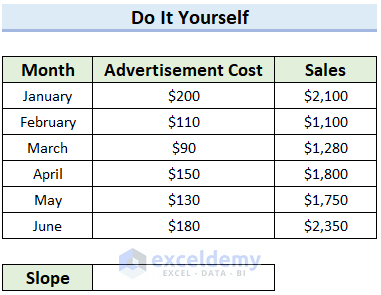
Practice Section
Here, I have provided a practice sheet for you to practice how to find the slope of a regression line in Excel.
Download Practice Workbook
Conclusion
So, you have reached the end of my article. Here, I tried to explain how to find the slope of a regression line in Excel in 3 quick ways. I hope this article was helpful to you. If you have any questions, feel free to let me know in the comment section below.
Related Articles
- How to Find Slope of Tangent Line in Excel
- How to Calculate Slope of Exponential Graph in Excel
- How to Calculate Slope and Intercept in Excel
<< Go Back to Excel SLOPE Function | Excel Functions | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!