The Effective Interest Rate reflects the true annual yield or cost of an investment or loan gainable or payable due to the compounding over the period. The IRR, XIRR, and EFFECT functions and the conventional effective interest rate formula can calculate the effective interest rate.
Effective Interest Rate with Example
The effective interest rate is the interest rate that you get or have to pay on your investment or for your loan. For a given interest rate and frequency of compounding within a year,
= (1 + i/n)n – 1The offered Interest Rate = i
And Frequency of the Compounding in a Year = n
You took a loan of $10,000 from a local bank with an annual percentage rate of 12%.
The interest will be compounded every month. To understand this concept:
Annual Percentage Rate/Nominal Interest Rate: 12%
The monthly interest rate: 12%/12 = 1%
At the end of Month 1: your Principal + Interest will be: $10,000 + $10,000 x 1% = $10,000 (1 + 0.01) = $10100
If you did not pay the interest ($100) for the first month, in the 2nd month your principal will be $10,100.
At the end of Month 2: your Principal + Interest will be = $10100 + $10100 x 1% = $10201
To create a formula from the above statement:
= $10100 + $10100 x 1%
= $10100 (1 + 1%)
= $10,000 x (1 + 1%) x (1 + 1%); As $10100 = $10,000 x (1 + 1%)
= $10,000 x (1 + 1%) ^2; As (1 + 1%) x (1 + 1%) = (1 + 1%) ^2
= $10,000 x (1 + 0.01) ^ 2
At the end of the 3rd month, your Principal + Interest will be: $10,000 x (1 + 0.01) ^ 3
… … …
… … …
… … …
After 12 months, your Principal and Interest will be: $10,000 x (1 + 0.01) ^12 = $11268.25
You are going to pay a total interest: ($11268.25 – $10,000) / $10,000 = 12.68%.
The bank indicated an Annual Percentage Rate of 12%.
That is the Nominal Interest Rate, but due to compound interest monthly, you’re paying more than the nominal interest rate. This interest rate is called the Effective Interest Rate.
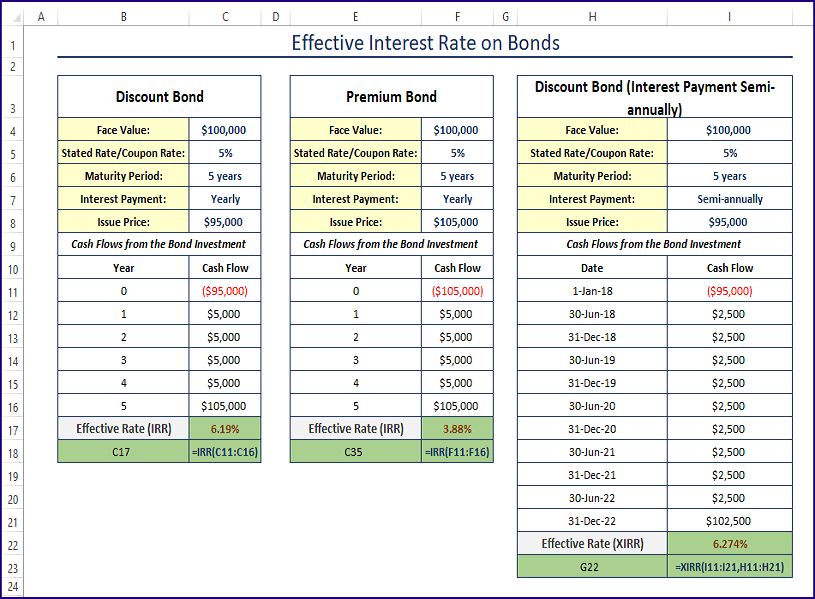
Method 1 – Using the IRR Function to Calculate the Effective Interest Rate On Discount Bonds
The Effective Interest Rate is the same as the Internal Rate of Return. The IRR function that calculates the Internal Rate of Return can be used to calculate the Effective Interest Rate.
If money is invested in a Discount Bond, use the IRR function to find the Effective Interest Rate.
The syntax of the IRR function is
IRR (values, [guess])The details of the discount bond are depicted in the image below.
Steps:
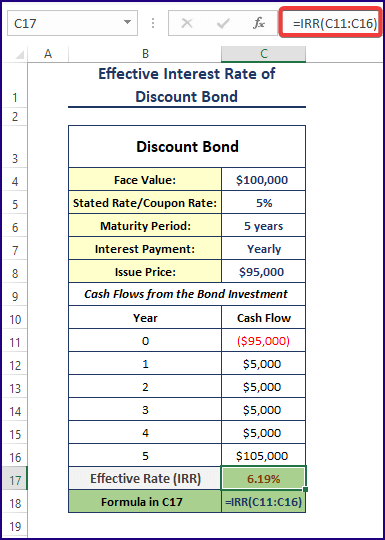
Enter the following formula in C17.
=IRR(C11:C16)Formula Breakdown
- In year 0, you invest $95,000 (the issue price of the bond) to buy the bond. You pay $95,000 because it’s a discount bond.
- At the end of the 1st year, you get $5,000 as the interest payment from the bond issuer. The face value of the bond is $100,000 and the nominal yearly interest rate is 5%. You get an interest payment amount of: $100,000 x 5% = $100,000 x 0.05 = $5,000.
- After the 2nd, 3rd, and 4th years, you get interest payments of $5,000.
- At the end of the 5th year, you get $105,000. Because your bond has matured. You get back the face value of the bond, of $100,000 + the yearly interest of $5,000 = $105,000.
- The IRR (Internal Rate of Return) or the Effective Interest Rate was calculated in C17: =IRR (C11: C16)
Method 2 – Calculating the Effective Interest Rate for Premium Bonds in Excel
The basic components of the premium bond are shown below.
Steps:
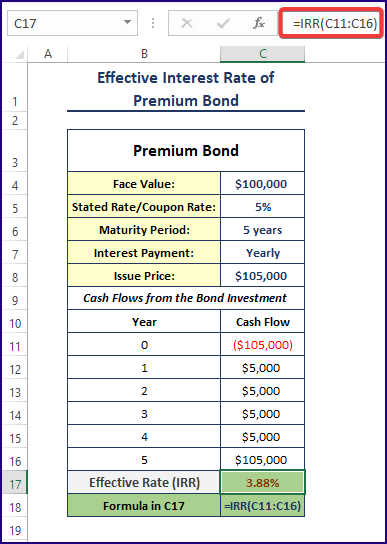
Use the formula in any blank cell (here, C17).
=IRR(C11:C16)Formula Breakdown
- The issue price is $105,000. In year 0, the investment is -$105,000.
- After years 1, 2, 3, and 4, the bondholder will get $5,000 in interest payments. The bond’s face value is $100,000 and its yearly nominal interest rate is 5%. The yearly interest payment is $100,000 x 5% = $5,000.
- At the end of year 5, the bond will mature. The bondholder will get the face value amount and the yearly interest payment: $100,000 + $5,000 = $105,000.
- The IRR function was used to calculate the internal rate of return or effective interest rate for these cash flows in C17: =IRR (C11: C16).
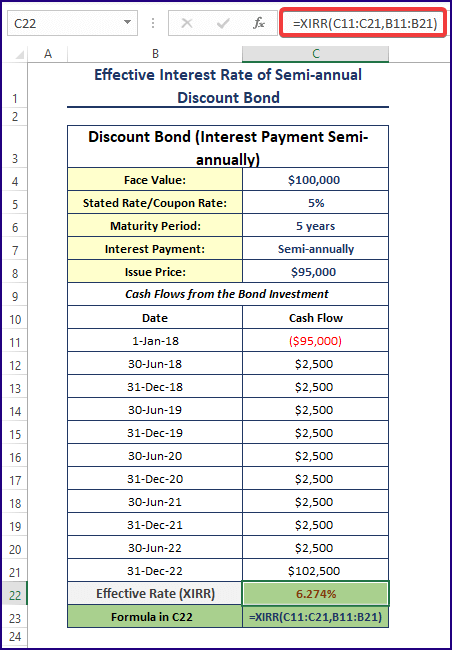
Method 3 – Finding the Effective Interest Rate for Semi-annually Payments
The XIRR function returns the internal rate of return for a schedule of cash flows. The syntax of the XIRR function is
XIRR (values, dates, [guess])The fundamental components of the discount bond are shown below.
Steps: Use the following formula in C22.
=XIRR(C11:C21,B11:B21)Formula Breakdown
- As the interest payments are done semi-annually (twice a year), the stated rate/nominal interest rate of 5% is divided by 2: 2.5%. The semi-annual interest payment will be $100,000 x 2.5% = $2,500.
- When the bond matures, you will get $102,500 (face value + the last 6 months’ interest). To get the internal rate of return or the effective rate of these cash flows, use Excel’s XIRR function.
- C11: C21 are the cash flows received, and B11: B21 is the date of receiving the cash flows. 6.274% is the effective interest rate for these cash flows.
Read More: How to Perform Interest Rate Swap Calculation in Excel
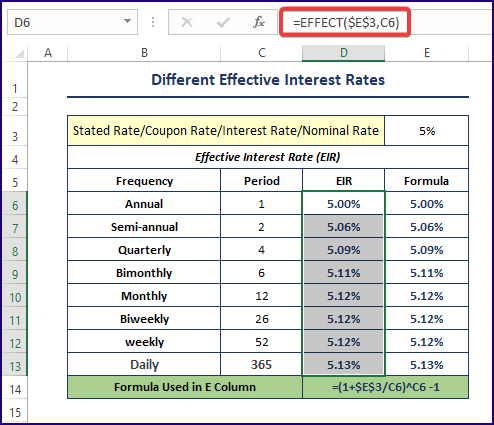
Method 4 – Applying the EFFECT Function to Calculate Different Effective Interest Rates
To calculate the Effective Interest Rates only, use the EFFECT function.
The syntax of the EFFECT function is:
EFFECT(rate,periods)Steps:
Use the following formula to calculate the effective interest rates for a given interest rate and frequencies.
=EFFECT($E$3,C6)Use the typical Effective Interest Rate formula ( (1 + i/n)n – 1) in the adjacent cell to cross-check the EFFECT function’s outcomes.
Download Excel Workbook
Related Articles
- Create Flat and Reducing Rate of Interest Calculator in Excel
- How to Perform Interest Rate Sensitivity Analysis in Excel
<< Go Back to Interest Rate Calculator | Finance Template | Excel Templates
Get FREE Advanced Excel Exercises with Solutions!




I want printed materials for courses
You can copy the article and paste in a word file and then use it personally. Thanks.