How to Convert Complex Numbers to Polar Form in Excel

This article will illustrate how to deal with the polar form of complex numbers in Excel.

Introduction to the Polar Form of Complex Numbers

We all know that complex numbers are commonly written in x+iy format. Here, i stands for √(-1), x is the real number part and y is the imaginary coefficient.

In mathematics, we can plot complex numbers in the Cartesian (x,y) and Polar (r,θ) coordinate systems. In this article, we will focus just on the polar form of complex numbers.

For example, let’s assume a complex number,

z=3+4i

If I plot this number in a Cartesian coordinate system, it will be like the following image.

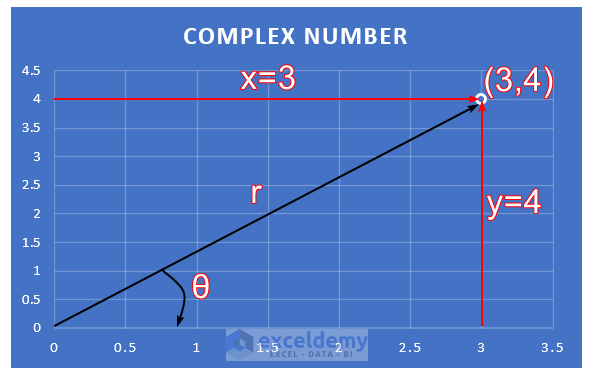
Look at the image carefully. If you add a line from (0,0) to (3,4), it will be the hypotenuse of a right-angle triangle whose base and vertical are x and y respectively.

So, hypotenuse, r= √(x2+y2); according to the Pythagorean theorem.

If the hypotenuse makes an angle θ, the θ= tan-1(y/x) or arctan(y/x)

Now, z=x+iy

So for the complex number, z=3+4i, x=3, and y=4.

If we substitute x and y in terms of r, x will be rcosθ and y will be rsinθ.

So, z=rcosθ+yisinθ

⇒ z=r(cosθ+isinθ)

∴ r=√(x2+y2)=√(25)=5

And θ= arctan(y/x)=arctan(4/3)=53°.

So the polar form of the number is:

5(cos53°+isin53°)

How to Convert Complex Numbers to Polar Form in Excel: Step-by-Step Procedures

In this section, we will see how to convert complex numbers to polar form in excel using COMPLEX, IMABS, and IAMARGUMENT functions. Look at the following dataset first.

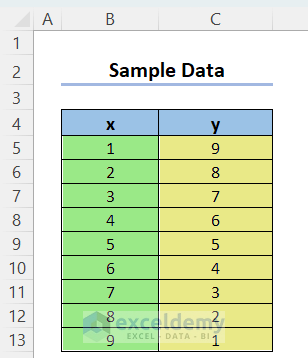
We have some x and y values in an Excel spreadsheet. We will convert them into complex numbers in Rectangular form first, then we will convert them into polar form.

⦿ Step 1: Generate Complex Numbers Using the COMPLEX Function

Use the following formula to convert input numbers to form some complex numbers.

=COMPLEX(B5,C5,"i")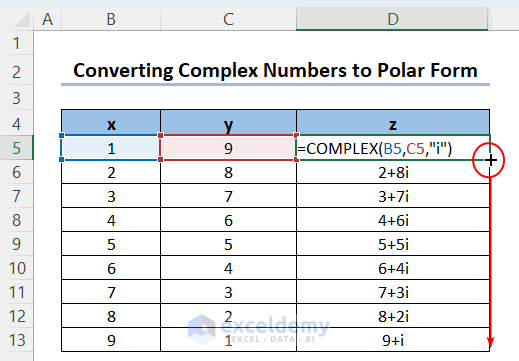

Here, the syntax of COMPLEX function is: =COMPLEX(real_num,i_num,[suffix])

So, the value in cell B5 is the real number part, and value in cell C5 is the imaginary coefficient part, and the last argument is optional (enclosed by []). You can fix either i or j as the imaginary number indicator.

Drag the fill handle icon to get the rest of the outputs.

⦿ Step 2: Convert Complex Numbers to Polar Form

Now, use the following formula to convert the complex numbers generated in the first step to polar form using the following formula.

=ROUNDDOWN(IMABS(D5),2)&"(cos "&ROUNDDOWN(DEGREES(IMARGUMENT(D5)),2)&CHAR(176)&" +isin "&ROUNDDOWN(DEGREES(IMARGUMENT(D5)),2)&CHAR(176)&")"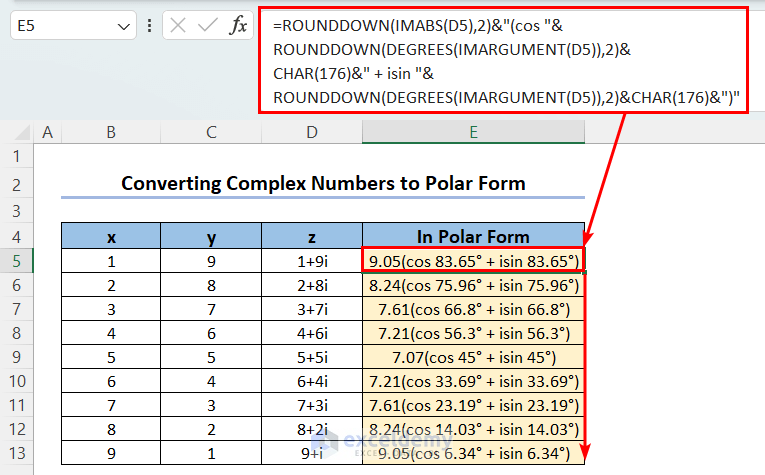

Drag the fill handle icon now.

⧪ Formula Explanation:

To explain the formula, let’s first look at the first output.

It’s: 9.05(cos 83.65° + isin 83.65°)

We have made this formula using IMABS & IMARGUMENT functions. The rest of the functions used here (ROUNDDOWN, DEGREES, and CHAR functions) are used to make the output look better.

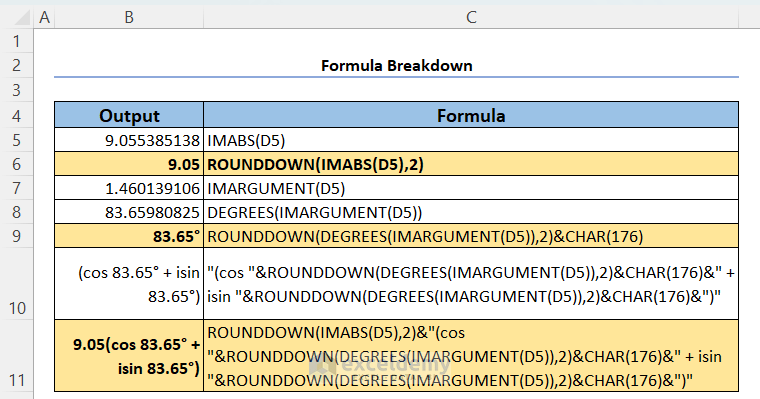
The IMABS function returns the modulus (r) of a complex number. So IMABS(D5) will return the modulus of the complex number in cell D5. The ROUNDDOWN function outside will just format the output to two-decimal digits.
The IMARGUMENT function returns the argument or θ angle of a complex number’s polar form. Since Excel uses radian unit for angle by default and there is no way to change this default setting, we have used the DEGREES function to make them look better. To show the degree (°) symbol, we have added CHAR(176) formula inside the larger formula.

You could use the following formula to avoid the extra functions used here:

=IMABS(D5)&"(cos "&IMARGUMENT(D5)&" + isin "&IMARGUMENT(D5)&")"

The output will be: 9.05538513813742(cos 1.460139105621 + isin 1.460139105621)

How to Convert Complex Numbers from Polar to Rectangular Form in Excel

Now, let’s deal with a reverse case. We have some complex numbers in polar form (angle in radian unit) this time and want them in rectangular form.

How to do that?

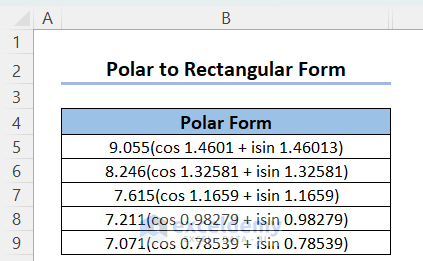
🔀 Steps:

Extract the magnitude or modulus from the polar form using the following formula.

=VALUE(LEFT(B5,5))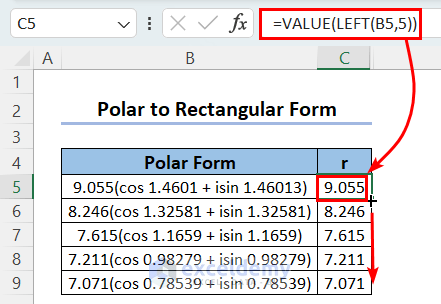

Next, extract the argument θ using the following formula.

=VALUE(MID(B5,FIND("cos",B5)+3,8))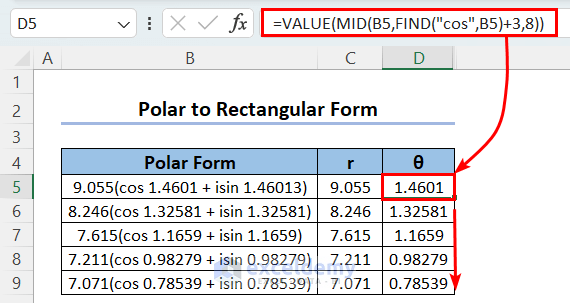

After that, use the following formula to get the rectangular complex number formats.

=IMEXP(COMPLEX(LN(C5),D5,"i"))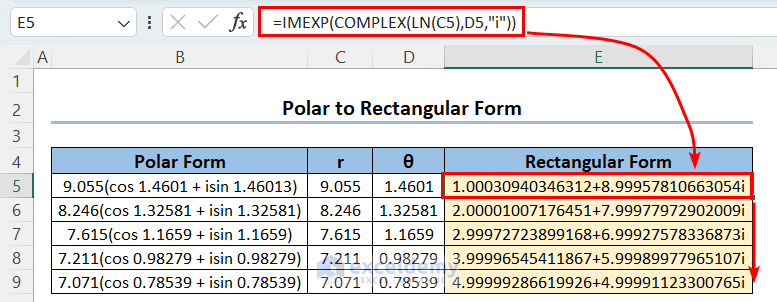

Download Practice Workbook

You can download the following workbook for your practice from the link below.

Complex Numbers in Polar Form.xlsx

Conclusion

So, we have discussed the polar form of complex numbers, and how to convert Complex Numbers to Polar form and Vice Versa. If this article is helpful, please leave us feedback in the comment box.

<< Go Back to | Complex Number in Excel | Excel for Math | Learn Excel

Get FREE Advanced Excel Exercises with Solutions!