How to Calculate Z-Score with a 95 Confidence Interval in Excel

The manual calculation process of the Z score:

Steps:

Choose a dataset. Here, we use a simple dataset with five values: 82, 77, 85, 78, and 80.
Estimate the simple Mean of this dataset.

Calculating mean value of the dataset manually

Evaluate the Standard Deviation of our data.
The standard deviation is 2.87, which indicates that the dataset is normally distributed.

Choose your desired confidence level interval. For our data, we set it at 95%.
In the Z-Score chart, we must find the value of 0.975 (e.g., 0.95+(0.05/2)=0.975).
You may notice that the Vertical Axis value for 0.975 is 1.9 and the Horizontal Axis value is 0.06.

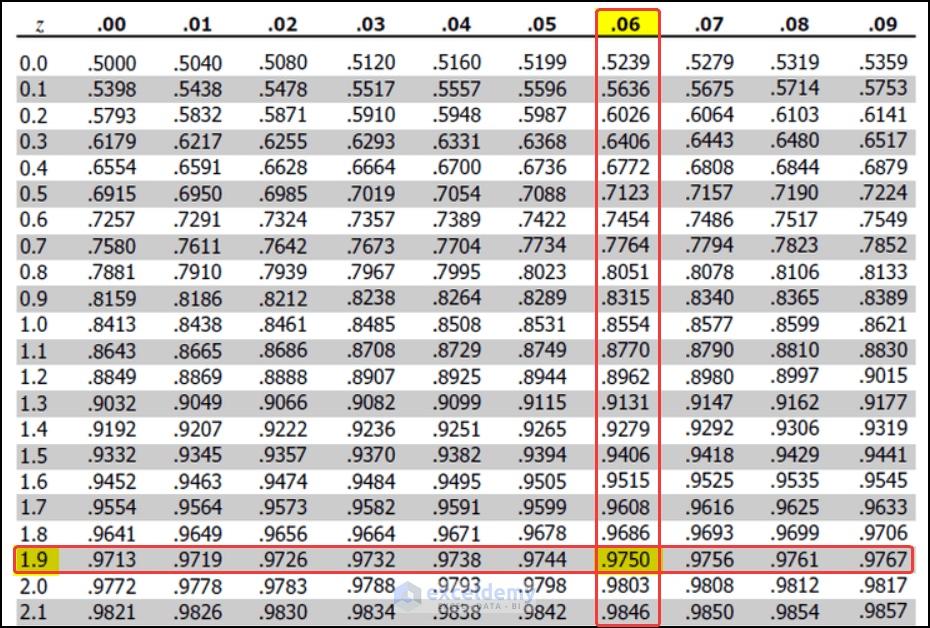
Evaluating Z-score value manually

Our 95% confidence interval Z-score value will be 1.9+0.06 = 1.96.

We can estimate the Z score with a 95 confidence interval manually.

Step-by-Step Procedure

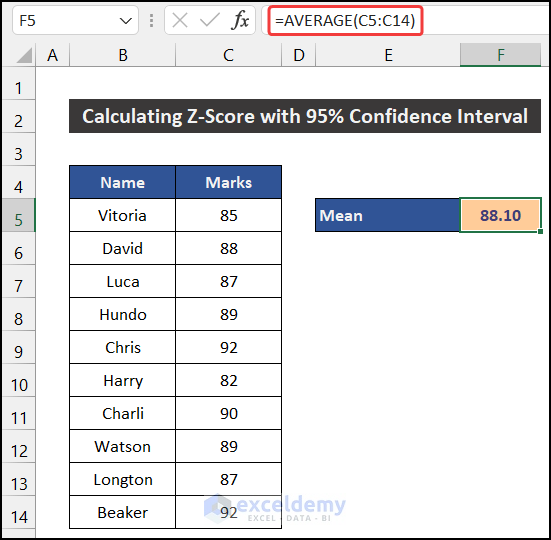
Step 1: Calculate the Mean of the Dataset

Select cell F5.
Enter the following formula in the cell:

=AVERAGE(C5:C14)

Press Enter.

You will get the mean value of our dataset.

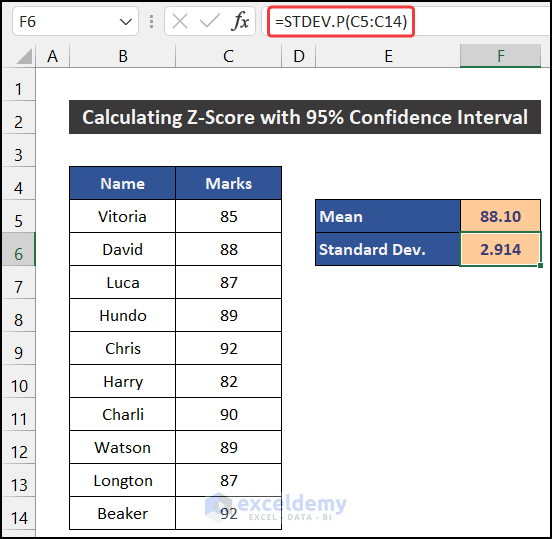
Step 2: Estimate Standard Deviation

Select cell F6.
Enter the following formula in the cell:

=STDEV.P(C5:C14)

Press Enter.

You will get the value of the Standard Deviation.
You may notice that the Standard Deviation is 2.914. We can decide whether our dataset will be normally distributed.

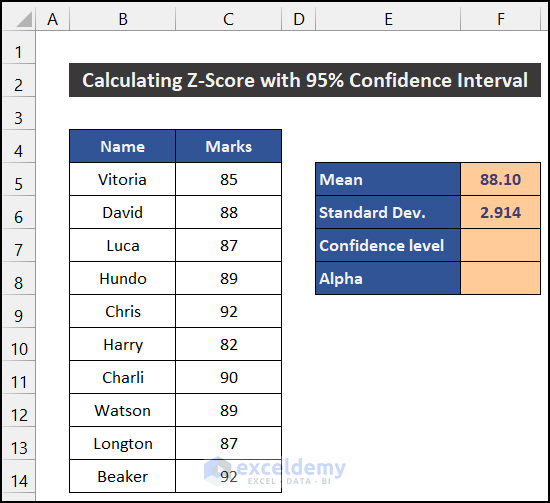
Step 3: Define the Confidence Interval Level

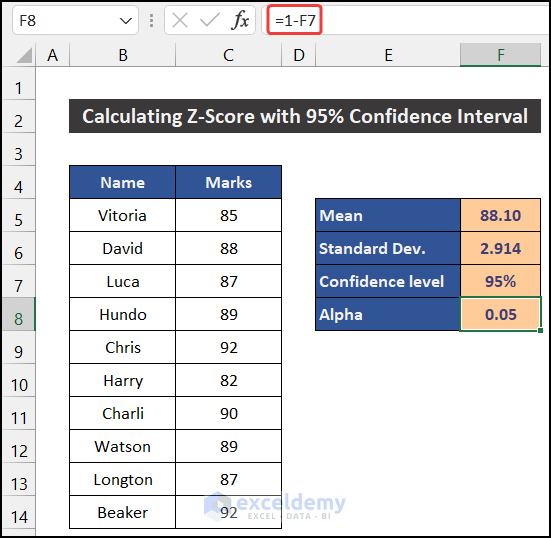
Title cells E7 and E8 as Confidence level and Alpha.

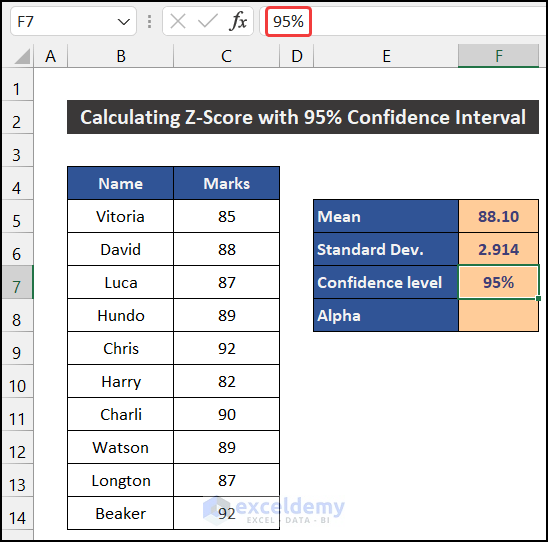
In cell F7, define the Confidence level. Here, we define our confidence interval as 95%.

Enter the following formula to get the Alpha value in cell F7:

=1-F7

Press Enter.

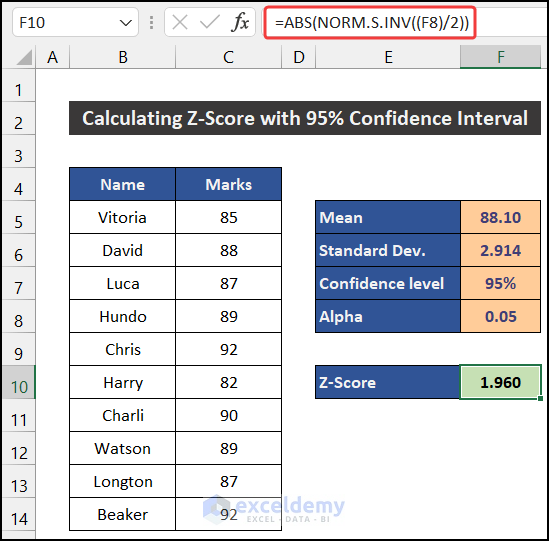
Step 4: Estimate the Z Score for the Desired Confidence Interval

Select cell F10.
Enter the following formula in the cell:

=ABS(NORM.S.INV((F8)/2))

Press Enter.

You will get the Z score value with a 95 confidence interval level, equal to the manual procedure.

Breakdown of the Formula

We are breaking down the formula for cell F10.

NORM.S.INV((F8)/2): The NORM.S.INV function gives us the Z-score value of 0.025. The value will show a negative sign as this interval level is at the right side of the mean position. Here, the function returns -1.960.

ABS(NORM.S.INV((F8)/2)): The ABS function will show the absolute value of the result of the NORM.S.INV function. For this cell, the function returns 1.960.

Download the Practice Workbook

Download this workbook for practice.

Z Score with 95 Confidence Interval.xlsx

<< Go Back to Statistical Significance in Excel | Excel for Statistics | Learn Excel

Get FREE Advanced Excel Exercises with Solutions!